问题描述

给你一个字符串 s，找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

示例1

输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。

示例2

输入：s = “cbbd”
输出：“bb”

提示

• 1 <= s.length <= 1000
• s 仅由数字和英文字母组成

思路分析

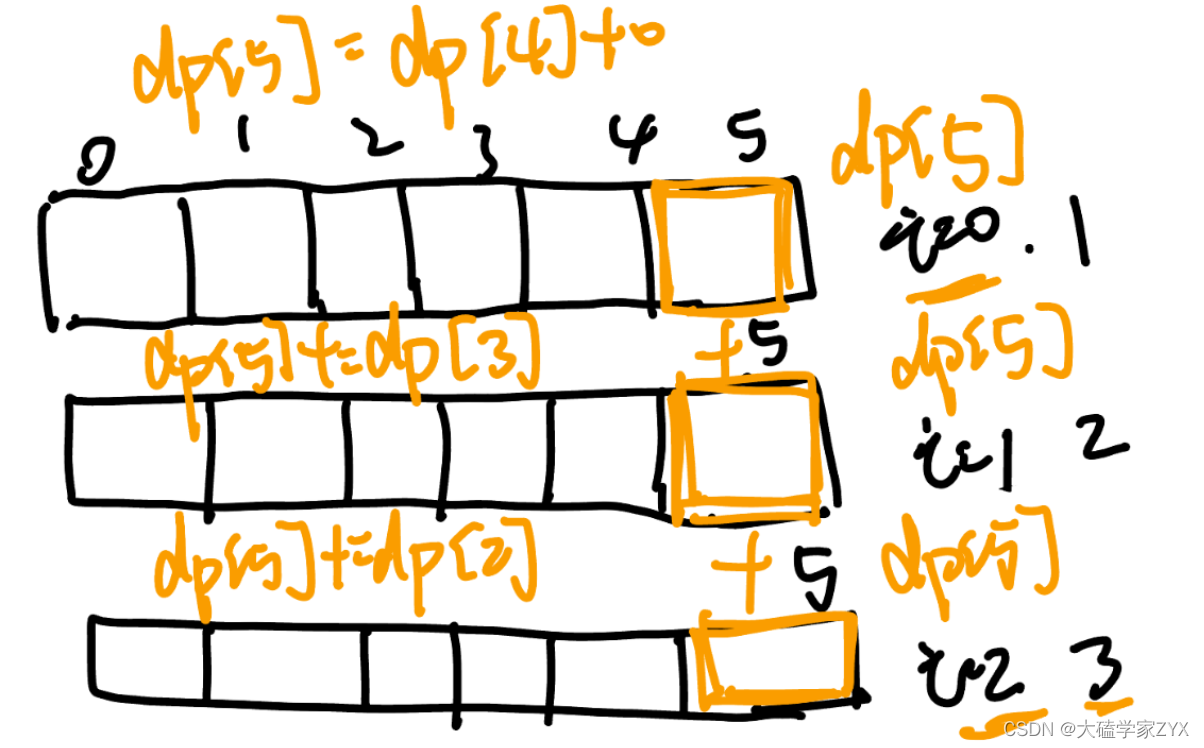
我们可以使用动态规划来解决这个问题。首先，定义一个二维数组 dp，其中 dp[i][j] 表示从索引 i 到索引 j 的子串是否是回文串。如果子串是回文串，则 dp[i][j] 的值为 True，否则为 False。

根据回文串的定义，我们可以得到以下推导公式：

• 如果一个字符串的首尾字符不相等，则它肯定不是回文串，即：dp[i][j] = False。
• 如果一个字符串的首尾字符相等，并且去掉首尾字符后的子串是回文串，则它也是回文串，即：dp[i][j] = dp[i+1][j-1]。

接下来，我们需要考虑边界条件。当子串的长度为 1 或 2 时，只需要判断首尾字符是否相等即可。因此，有以下边界条件：

• 当 j - i + 1 = 1，即子串长度为 1 时，表示该字符本身就是回文串，即：dp[i][j] = True。
• 当 j - i + 1 = 2，即子串长度为 2 时，如果首尾字符相等，则该子串也是回文串，即：dp[i][j] = (s[i] == s[j])。

最后，我们遍历字符串 s，根据以上推导公式计算 dp 数组的值，并记录最长的回文子串。

代码分析

1. 首先，判断输入字符串 s 的长度是否为 0，如果是，则直接返回空字符串。
2. 接着，初始化变量 n，表示字符串 s 的长度，并创建一个二维数组 dp，大小为 n × n，用于存储回文子串的判断结果。
3. 然后，初始化变量 start 和 max_len，表示最长回文子串的起始位置和长度，初始值均为 0。
4. 对于单个字符来说，它本身就是回文串，所以将 dp[i][i] 设置为 True。
5. 接下来，通过两层循环遍历字符串 s，其中，外层循环变量 j 表示右边界，内层循环变量 i 表示左边界。
6. 在循环过程中，对于每个子串的首尾字符进行判断：
   • 如果首尾字符不相等，即 s[i] != s[j]，则该子串不是回文串，将 dp[i][j] 设置为 False。
   • 如果首尾字符相等，即 s[i] == s[j]，则判断去掉首尾字符后的子串是否是回文串，即 dp[i+1][j-1]，如果是，则当前子串也是回文串，将 dp[i][j] 设置为 True。
   • 同时，更新最长回文子串的起始位置和长度，并记录下来。
7. 循环结束后，返回字符串 s 中最长回文子串，即 s[start:start + max_len]。

完整代码

class Solution(object):
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        n = len(s)
        if n == 0:
            return ""

        # 初始化dp数组
        dp = [[False] * n for _ in range(n)]  # 创建一个大小为n×n的二维数组dp，用于存储回文子串的判断结果

        # 初始化最长回文子串的起始位置和长度
        start = 0
        max_len = 1

        # 单个字符一定是回文串，将dp[i][i]设置为True
        for i in range(n):
            dp[i][i] = True

        # 遍历字符串，计算dp数组的值
        for j in range(1, n):  # 外层循环变量j表示右边界
            for i in range(j):  # 内层循环变量i表示左边界
                if s[i] == s[j]:
                    # 当前字符首尾相等，如果去掉首尾字符后的子串也是回文串，则当前子串也是回文串
                    if j - i + 1 <= 2 or dp[i + 1][j - 1]:
                        dp[i][j] = True
                        # 更新最长回文子串的起始位置和长度
                        if j - i + 1 > max_len:
                            max_len = j - i + 1
                            start = i

        return s[start:start + max_len]  # 返回最长回文子串

详细分析

1. 首先，判断输入字符串 s 的长度是否为 0，如果是，则直接返回空字符串。

n = len(s)
if n == 0:
    return ""

2. 接着，初始化变量 n，表示字符串 s 的长度，并创建一个二维数组 dp，大小为 n × n，用于存储回文子串的判断结果。

n = len(s)
dp = [[False] * n for _ in range(n)]

3. 然后，初始化变量 start 和 max_len，表示最长回文子串的起始位置和长度，初始值均为 0。

start = 0
max_len = 1

4. 对于单个字符来说，它本身就是回文串，所以将 dp[i][i] 设置为 True。

for i in range(n):
    dp[i][i] = True

5. 接下来，通过两层循环遍历字符串 s，其中，外层循环变量 j 表示右边界，内层循环变量 i 表示左边界。

for j in range(1, n):
    for i in range(j):

6. 在循环过程中，对于每个子串的首尾字符进行判断：
   • 如果首尾字符不相等，即 s[i] != s[j]，则该子串不是回文串，将 dp[i][j] 设置为 False。
   • 如果首尾字符相等，即 s[i] == s[j]，则判断去掉首尾字符后的子串是否是回文串，即 dp[i+1][j-1]，如果是，则当前子串也是回文串，将 dp[i][j] 设置为 True。

if s[i] == s[j]:
    if j - i + 1 <= 2 or dp[i + 1][j - 1]:
        dp[i][j] = True

7. 同时，更新最长回文子串的起始位置和长度，并记录下来。

if j - i + 1 > max_len:
    max_len = j - i + 1
    start = i

8. 循环结束后，返回字符串 s 中最长回文子串，即 s[start:start + max_len]。

return s[start:start + max_len]

这样，就完成了找到字符串中最长回文子串的任务。

运行效果截图

调用示例

solution = Solution()
s = "babad"
s1 = "cbbd"
print(solution.longestPalindrome(s))

print(solution.longestPalindrome(s1))

运行结果

完结