文章目录

2140. 解决智力问题
- 解法1——倒序DP（填表法）
- 解法2——正序DP（刷表法）⭐⭐⭐
2167. 移除所有载有违禁货物车厢所需的最少时间⭐⭐⭐
- 解法1——前缀和⭐⭐⭐⭐⭐
- 解法2——前后缀分解 + 动态规划
- - 代码1——看了思路之后自己写的
  - 代码2——代码1的优化（一次遍历）⭐
2172. 数组的最大与和（状态压缩DP）⭐⭐⭐⭐⭐
- 思路
- 代码
- 补充：相似题目——1879. 两个数组最小的异或值之和⭐⭐⭐
2188. 完成比赛的最少时间⭐⭐⭐⭐⭐
- 思路——结合性质巧妙线性DP （预处理每种圈数的最短时间 + 动态规划）
- 代码
2209. 用地毯覆盖后的最少白色砖块⭐⭐⭐⭐⭐
- 思路——考虑是否使用第i条地毯且其末尾覆盖第j块板砖
- 代码
2218. 从栈中取出 K 个硬币的最大面值和（分组背包）🐂🐂🐂
- 分组DP模板
2246. 相邻字符不同的最长路径（树形DP）
- 思路——树形DP
- 代码
2262. 字符串的总引力⭐⭐⭐⭐⭐
- 思路——记录各个字母上次出现的位置，考虑增加的引力值
- 代码
2266. 统计打字方案数
- 分组 + 线性DP + 乘法原理
2272. 最大波动的子字符串⭐⭐⭐⭐⭐
- 思路——枚举最多和最少的字符+最大子数组和
- 代码
2305. 公平分发饼干（子集状态压缩DP）
- 解法1——dfs回溯+剪枝
- 解法2——子集状压DP⭐⭐⭐⭐⭐（很**重要**！值得一学）
- - 代码技巧——如何枚举一个集合的所有子集⭐🐂
  - 代码的空间优化
- 补充：相似题目练习——1723. 完成所有工作的最短时间
2312. 卖木头块⭐⭐⭐
- 解法1——记忆化搜索
- 解法2——线性DP
2318. 不同骰子序列的数目
- - 解法1——三维DP
  - 解法2——二维DP⭐
2320. 统计放置房子的方式数
- 代码1
- 代码2——变量代替dp数组
- 代码3——static代码块预处理
2321. 拼接数组的最大分数
- 转换成最大子数组和
LCP 53. 守护太空城（子集状压DP）⭐⭐⭐⭐⭐🚹🚹🚹🚹🚹

https://leetcode.cn/circle/discuss/G0n5iY/

2140. 解决智力问题

2140. 解决智力问题
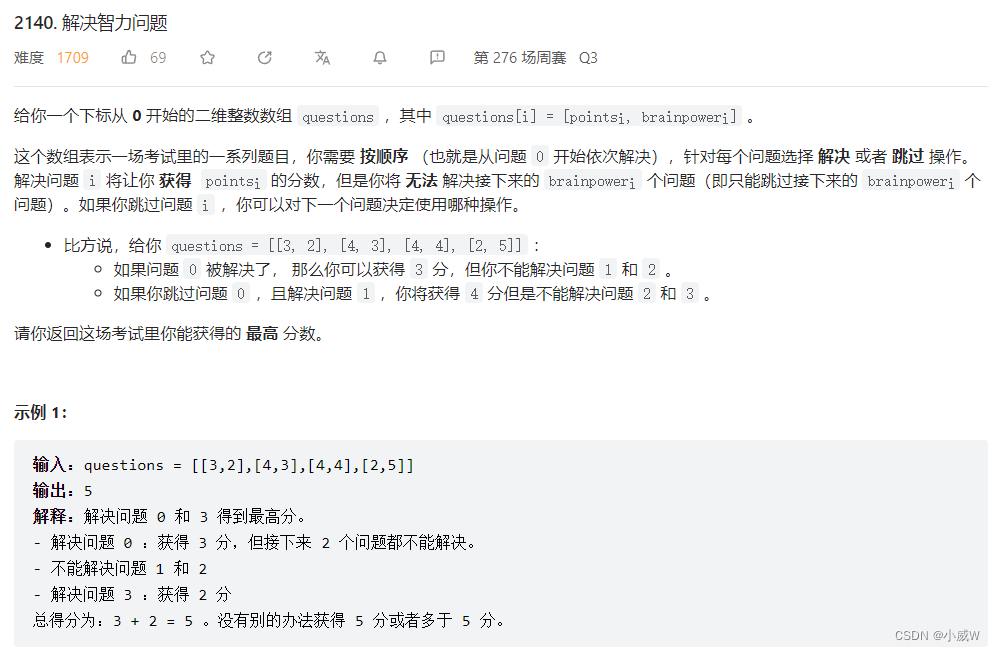
在这里插入图片描述

提示：

1 <= questions.length <= 10^5
questions[i].length == 2
1 <= pointsi, brainpoweri <= 10^5

解法1——倒序DP（填表法）

填表法适用于大多数 DP：通过当前状态所依赖的状态，来计算当前状态。

由于选择 i 时需要跳过后面的一部分，因此我们想要知道后面被选择的情况，所以倒序遍历会更加方便。

定义 f[i] 表示解决区间 [i,n−1] 内的问题可以获得的最高分数。

class Solution {
    public long mostPoints(int[][] questions) {
        int n = questions.length;
        long[] dp = new long[n];
        dp[n - 1] = questions[n - 1][0];    // dp[i]表示从i~n-1任意选择时的最大值
        for (int i = n - 2; i >= 0; --i) {
            // 计算选i的情况
            dp[i] = questions[i][0];
            if (i + questions[i][1] + 1 < n) dp[i] += dp[i + questions[i][1] + 1];
            // 与不选i的情况取最大值
            dp[i] = Math.max(dp[i], dp[i + 1]);
        }
        return dp[0];
    }
}

解法2——正序DP（刷表法）⭐⭐⭐

定义 f[i] 表示解决区间 [0,i) 内的问题可以获得的最高分数。
在这里插入图片描述

class Solution {
    public long mostPoints(int[][] questions) {
        int n = questions.length;
        long[] dp = new long[n + 1];
        for (int i = 0; i < n; ++i) {
            // 不选i
            dp[i + 1] = Math.max(dp[i + 1], dp[i]);
            // 选i
            int j = Math.min(n, i + questions[i][1] + 1);
            dp[j] = Math.max(dp[j], dp[i] + questions[i][0]);
        }
        return dp[n];
    }
}

居然还可以这样 dp？
枚举到 i 的时候可以不是更新 dp[i]，而是更新和它相关的另外一些位置。

2167. 移除所有载有违禁货物车厢所需的最少时间⭐⭐⭐

2167. 移除所有载有违禁货物车厢所需的最少时间
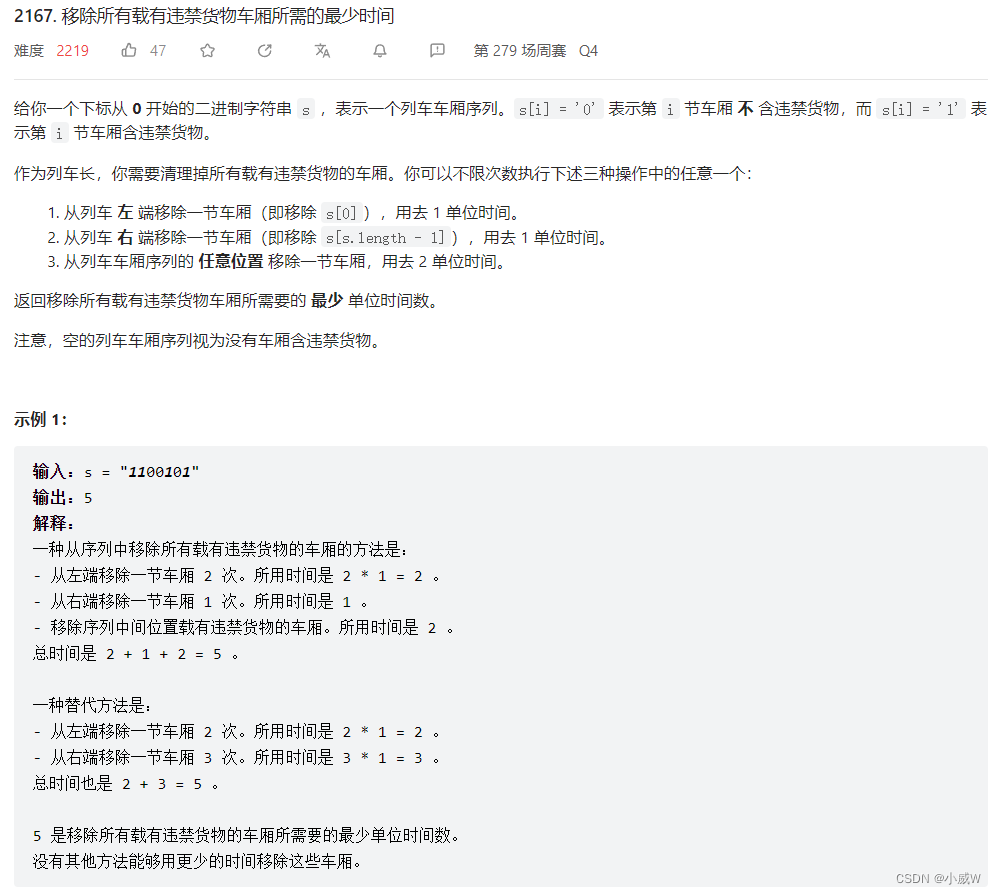
在这里插入图片描述

解法1——前缀和⭐⭐⭐⭐⭐

https://leetcode.cn/problems/minimum-time-to-remove-all-cars-containing-illegal-goods/solutions/1249244/yi-chu-suo-you-zai-you-wei-jin-huo-wu-ch-qinx/

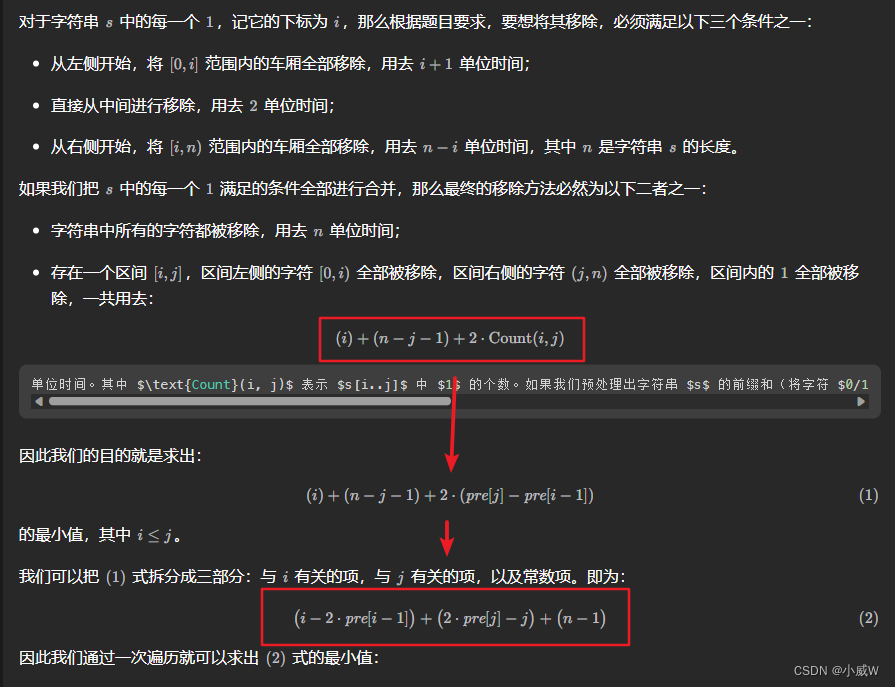
在这里插入图片描述

将求最后一个公式最小值的过程翻译成代码如下：

class Solution {
    public int minimumTime(String s) {
        int n = s.length(), preBest = 0, preSum = 0, ans = Integer.MAX_VALUE;
        for (int j = 0; j < n; ++j) {
            preBest = Math.min(preBest, j - 2 * preSum);
            preSum += (s.charAt(j) - '0');
            ans = Math.min(ans, preBest + 2 * preSum - j);
        }
        return ans + n - 1;
    }
}

解法2——前后缀分解 + 动态规划

在这里插入图片描述

代码1——看了思路之后自己写的

class Solution {
    public int minimumTime(String s) {
        int n = s.length();
        int[] dp1 = new int[n], dp2 = new int[n];
        dp1[0] = s.charAt(0) == '1'? 1: 0;
        dp2[n - 1] = s.charAt(n - 1) == '1'? 1: 0;
        for (int i = 1; i < n; ++i) {
            if (s.charAt(i) == '0') dp1[i] = dp1[i - 1];
            else dp1[i] = Math.min(dp1[i - 1] + 2, i + 1);
        }
        int ans = dp1[n - 1];
        for (int i = n - 2; i >= 0; --i) {
            if (s.charAt(i) == '0') dp2[i] = dp2[i + 1];
            else dp2[i] = Math.min(dp2[i + 1] + 2, n - i);
            ans = Math.min(ans, (i - 1 >= 0? dp1[i - 1]: 0) + dp2[i]);
        }
        return ans;
    }
}

代码2——代码1的优化（一次遍历）⭐

class Solution {
    public int minimumTime(String s) {
        int n = s.length();
        int ans = n, pre = 0;
        for (int i = 0; i < n; ++i) {
            if (s.charAt(i) == '1') pre = Math.min(pre + 2, i + 1);
            ans = Math.min(ans, pre + n - 1 - i);
        }
        return ans;
    }
}

2172. 数组的最大与和（状态压缩DP）⭐⭐⭐⭐⭐

2172. 数组的最大与和
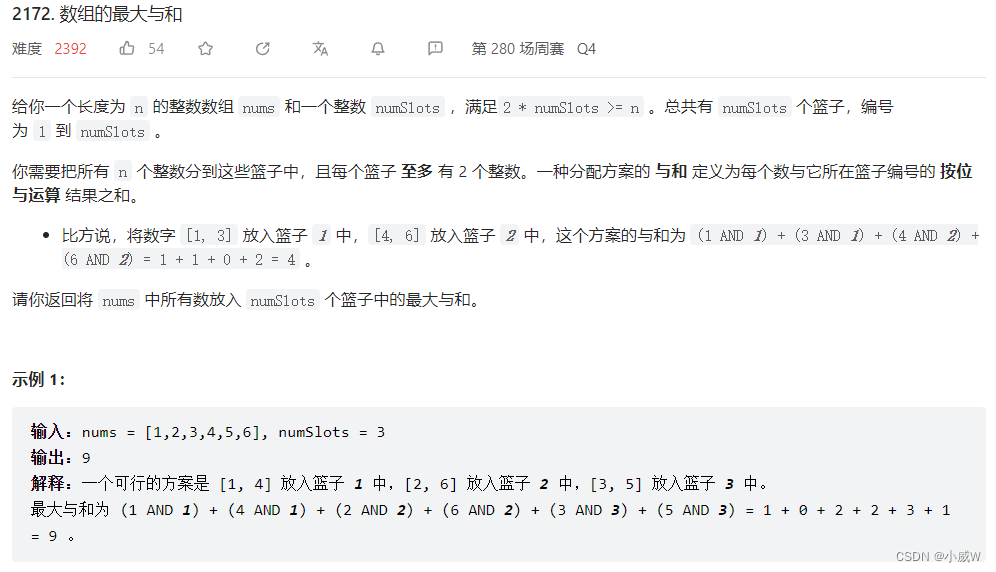
在这里插入图片描述

思路

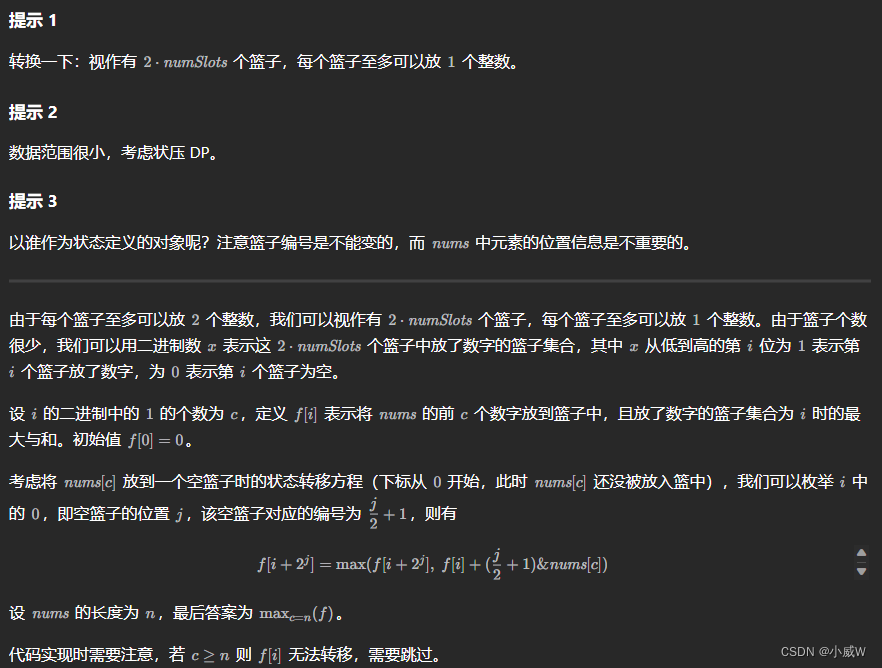
在这里插入图片描述
注意这里空蓝子的位置 j，对应的编号是 j / 2 + 1。
即位置 0, 1, 2, 3, 4, 5, 6, 7 会被映射成 1, 1, 2, 2, 3, 4, 4, 4。

代码

class Solution {
    public int maximumANDSum(int[] nums, int numSlots) {
        int n = nums.length, ans = 0;
        int[] dp = new int[1 << (numSlots * 2)];
        for (int i = 0; i < dp.length; ++i) {
            int c = Integer.bitCount(i);    // 1的个数,即已经放进篮子的数量
            if (c >= n) continue;
            for (int j = 0; j < numSlots * 2; ++j) {    // 枚举每个篮子(尝试是空蓝子的话放入nums[c])
                if ((i & (1 << j)) == 0) {              // 如果是空蓝子的话
                    int s = i | (1 << j);               // 在i的基础上放入j篮子
                    dp[s] = Math.max(dp[s], dp[i] + ((j / 2 + 1) & nums[c]));
                    ans = Math.max(ans, dp[s]);
                }
            }
        }   
        return ans;
    }
}

在循环 j 的过程中会尝试在每一个空蓝子中放入 nums[c]。

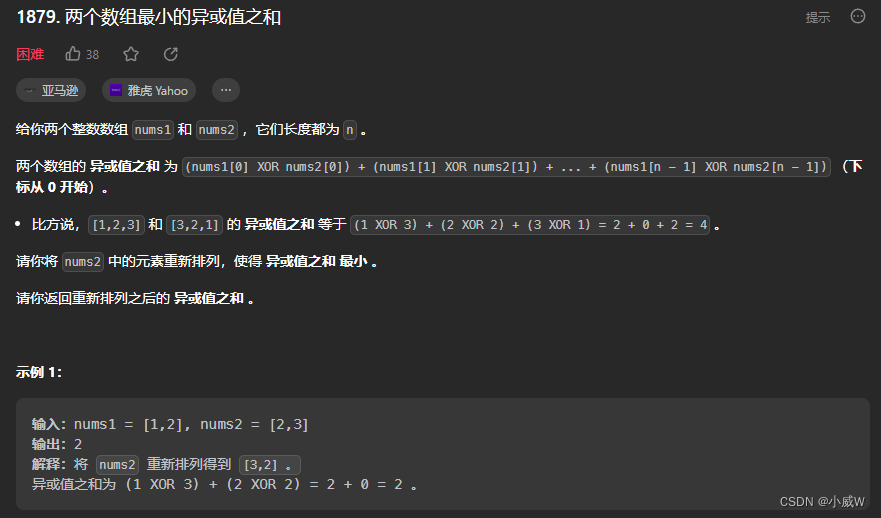
补充：相似题目——1879. 两个数组最小的异或值之和⭐⭐⭐

https://leetcode.cn/problems/minimum-xor-sum-of-two-arrays/
在这里插入图片描述

class Solution {
    public int minimumXORSum(int[] nums1, int[] nums2) {
        int n = nums1.length;
        int[] dp = new int[1 << n];
        Arrays.fill(dp, (int)2e9);
        dp[0] = 0;
        for (int mask = 1; mask < dp.length; ++mask) {
            int c = Integer.bitCount(mask);
            for (int j = 0; j < n; ++j) {
                if ((mask >> j & 1) == 1) {     // 检查这一位是否已经被设置了
                    // 如果已经被设置了，那就从没有被设置的状态转移过来
                    dp[mask] = Math.min(dp[mask], dp[mask ^ (1 << j)] + (nums1[c - 1] ^ nums2[j]));
                }
            }
        }
        return dp[dp.length - 1];
    }
}

代码中通过 mask ^ (1 << j) 将第 j 位的 1 去掉。

2188. 完成比赛的最少时间⭐⭐⭐⭐⭐

2188. 完成比赛的最少时间

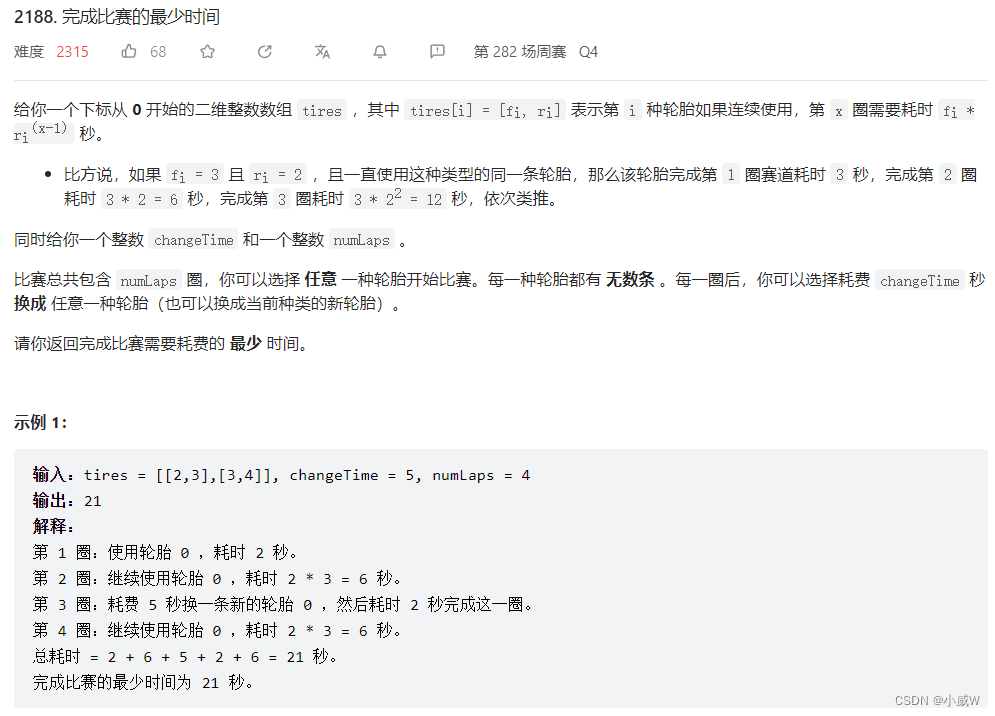
在这里插入图片描述

提示：

1 <= tires.length <= 10^5
tires[i].length == 2
1 <= fi, changeTime <= 10^5
2 <= ri <= 10^5
1 <= numLaps <= 1000

思路——结合性质巧妙线性DP （预处理每种圈数的最短时间 + 动态规划）

https://leetcode.cn/problems/minimum-time-to-finish-the-race/solutions/1295939/jie-he-xing-zhi-qiao-miao-dp-by-endlessc-b963/
在这里插入图片描述

代码

class Solution {
    public int minimumFinishTime(int[][] tires, int changeTime, int numLaps) {
        // minSec[i]表示连续使用同一个轮胎跑x圈的最小耗时
        int[] minSec = new int[18];     // 考虑题目数据范围，最多17圈就要换轮胎
        Arrays.fill(minSec, Integer.MAX_VALUE / 2);
        for (int[] tire: tires) {
            long f = tire[0], r = tire[1];
            for (int x = 1, sum = 0; f <= changeTime + tire[0]; ++x) {
                sum += f;
                minSec[x] = Math.min(minSec[x], sum);
                f *= r;     // 更新下一圈的花费
            }
        }
		
		// 动态规划
        int[] dp = new int[numLaps + 1];
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = -changeTime;	// 初始化值 方便后面的循环
        for (int i = 1; i <= numLaps; ++i) {
            for (int j = 1; j <= Math.min(17, i); ++j) {
                // i从i-j转移过来
                dp[i] = Math.min(dp[i], dp[i - j] + minSec[j]);
            }
            dp[i] += changeTime;
        }
        return dp[numLaps];
    }
}

2209. 用地毯覆盖后的最少白色砖块⭐⭐⭐⭐⭐

2209. 用地毯覆盖后的最少白色砖块
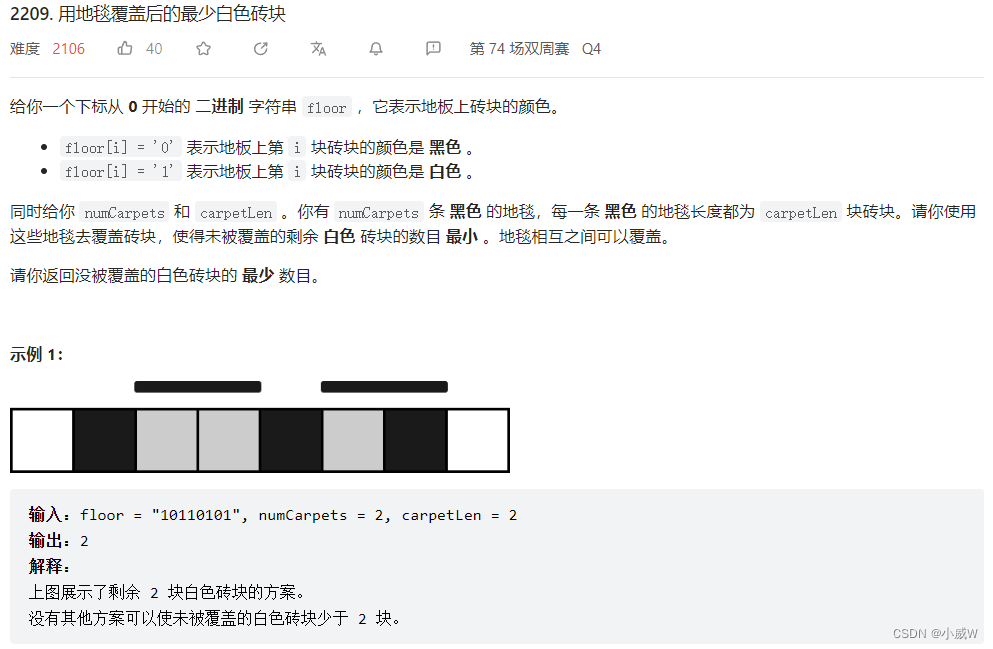
在这里插入图片描述

提示：

1 <= carpetLen <= floor.length <= 1000
floor[i] 要么是 '0' ，要么是 '1' 。
1 <= numCarpets <= 1000

思路——考虑是否使用第i条地毯且其末尾覆盖第j块板砖

在这里插入图片描述

代码

class Solution {
    public int minimumWhiteTiles(String floor, int numCarpets, int carpetLen) {
        int m = floor.length();
        if (numCarpets * carpetLen >= m) return 0;  // 全都能覆盖
        int[][] dp = new int[numCarpets + 1][m];    // 用前i个地毯覆盖前j个格子时，保留的最少白色砖块
        dp[0][0] = floor.charAt(0) % 2;             // 第0个地毯不能使用,即不能覆盖

        for (int i = 1; i < m; ++i) {
            dp[0][i] = dp[0][i - 1] + floor.charAt(i) % 2;  // 类似求前缀和的过程
        }
        for (int i = 1; i <= numCarpets; ++i) {             // 地毯
            for (int j = carpetLen * i; j < m; ++j) {       // 枚举格子
                // 不放在j或者放在j
                dp[i][j] = Math.min(dp[i][j - 1] + floor.charAt(j) % 2, dp[i - 1][j - carpetLen]);
            }
        }
        return dp[numCarpets][m - 1];
    }
}

2218. 从栈中取出 K 个硬币的最大面值和（分组背包）🐂🐂🐂

2218. 从栈中取出 K 个硬币的最大面值和
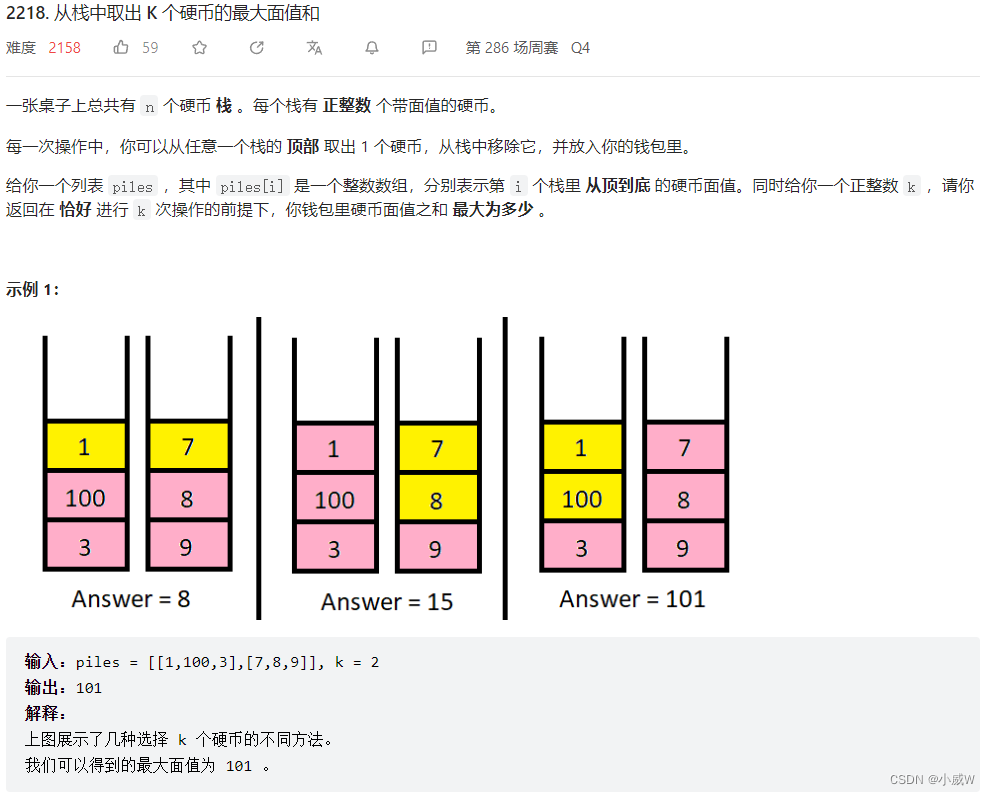
在这里插入图片描述

将问题转化成分组背包，每一个栈为一组。
每个组只能取出一个元素块，一个元素块即为栈顶的若干个元素。

class Solution {
    public int maxValueOfCoins(List<List<Integer>> piles, int k) {
        int n = piles.size();   // 有n个组
        int[] dp = new int[k + 1];
        for (List<Integer> pile: piles) {
            for (int i = 1; i < pile.size(); ++i) {
                // 将元素的价值修改为前缀和
                pile.set(i, pile.get(i - 1) + pile.get(i));
            }
        }

        for (int x = 0; x < n; ++x) {       // 循环每一组
            for (int i = k; i >= 1; --i) {  // 循环背包容量
                for (int j = 1; j <= piles.get(x).size(); j++) {     // 循环该组的每一个物品
                    if (i >= j) {
                        dp[i] = Math.max(dp[i], dp[i - j] + piles.get(x).get(j - 1));
                    }
                }
            }
        }
        return dp[k];
    }
}

分组DP模板

for (int k = 1; k <= ts; k++)           // 循环每一组
  for (int i = m; i >= 0; i--) // 循环背包容量
    for (int j = 1; j <= cnt[k]; j++)   // 循环该组的每一个物品
      if (i >= w[t[k][j]])  // 背包容量充足
        dp[i] = max(dp[i], dp[i - w[t[k][j]]] + c[t[k][j]]);  // 像0-1背包一样状态转移

资料来源：https://oi-wiki.org/dp/knapsack/#%E5%88%86%E7%BB%84%E8%83%8C%E5%8C%85

2246. 相邻字符不同的最长路径（树形DP）

2246. 相邻字符不同的最长路径
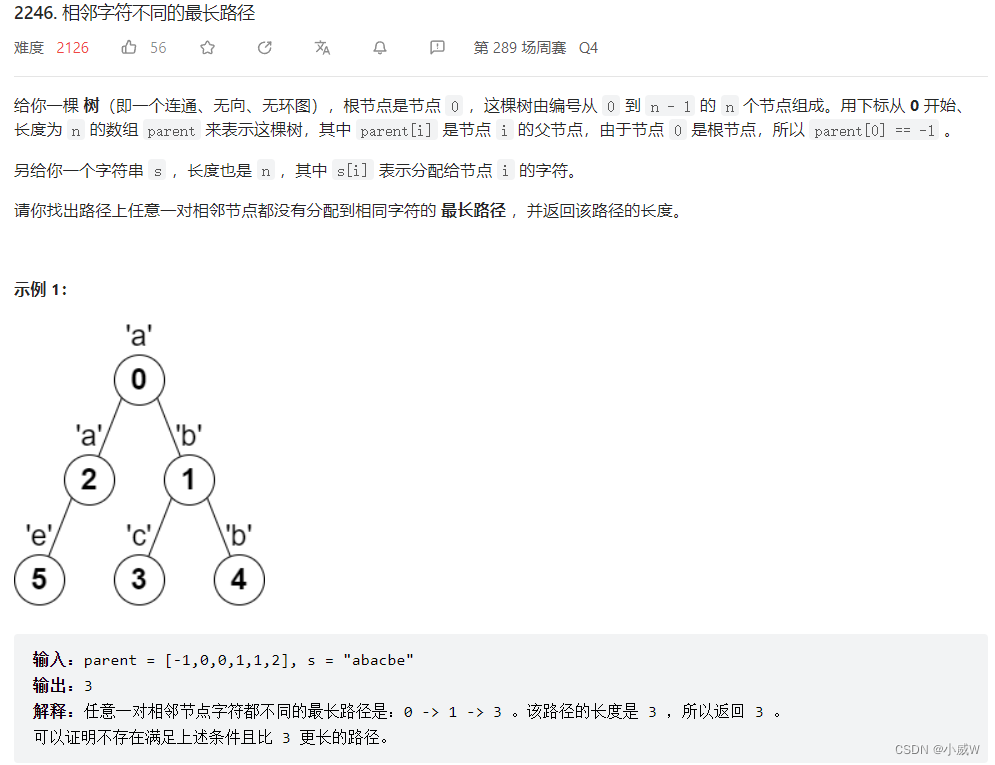
在这里插入图片描述

思路——树形DP

关于树形DP可见：
【算法】树形DP ①（树的直径）
【算法】树形DP ② 打家劫舍Ⅲ（树上最大独立集）

一道典型的树形DP，要求相邻节点不能相同。

这里的路径长度定义就是路径上节点的数量。

代码

下面这种代码风格适用于这种每个节点可能有多个孩子的树。

class Solution {
    List<Integer>[] g;
    char[] s;
    int ans = 1;

    public int longestPath(int[] parent, String s) {
        int n = parent.length;
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList());
        for (int i = 1; i < n; ++i) {
            g[parent[i]].add(i);
        }
        this.s = s.toCharArray();
        dfs(0, -1);
        return ans;
    }

    public int dfs(int x, int fa) {
        int mxL = 1;    // 这个节点往下的最长路径
        for (int child: g[x]) {
            if (child == fa) continue;
            int len = dfs(child, x);
            if (s[x] != s[child]) {
                ans = Math.max(ans, mxL + len); // 更新答案
                mxL = Math.max(mxL, len + 1);   // 更新当前往下的最长路径
            }
        }
        return mxL;     // 返回值是往下的最长路径
    }
}

2262. 字符串的总引力⭐⭐⭐⭐⭐

2262. 字符串的总引力
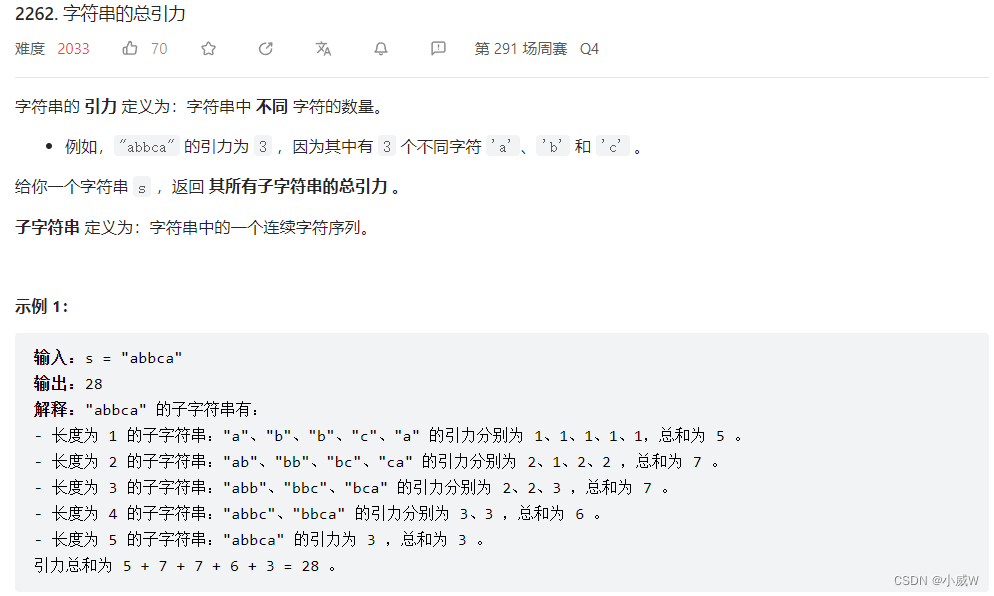
在这里插入图片描述

提示：
1 <= s.length <= 10^5
s 由小写英文字母组成

思路——记录各个字母上次出现的位置，考虑增加的引力值

从左往右遍历，考虑将 s[i] 加到 s[i - 1] 末尾之后，以 s[i] 为末尾的字符的引力值在以 s[i - 1] 为末尾的字符串的引力值的基础上增加了多少。

如果 s[i] 的字符在此前都没有出现过，那么引力值会增加 i。
如果出现过且下标为 j，那么引力值会增加 i - j。

代码

class Solution {
    public long appealSum(String s) {
        long ans = 0;
        int[] last = new int[26];
        Arrays.fill(last, -1);      // 记录各个字母上次出现的位置
        for (int i = 0, sumG = 0; i < s.length(); ++i) {
            int ch = s.charAt(i) - 'a';
            sumG += i - last[ch];	// i - last[ch]是增加的引力值
            ans += sumG;			
            last[ch] = i;
        }
        return ans;
    }
}

2266. 统计打字方案数

2266. 统计打字方案数
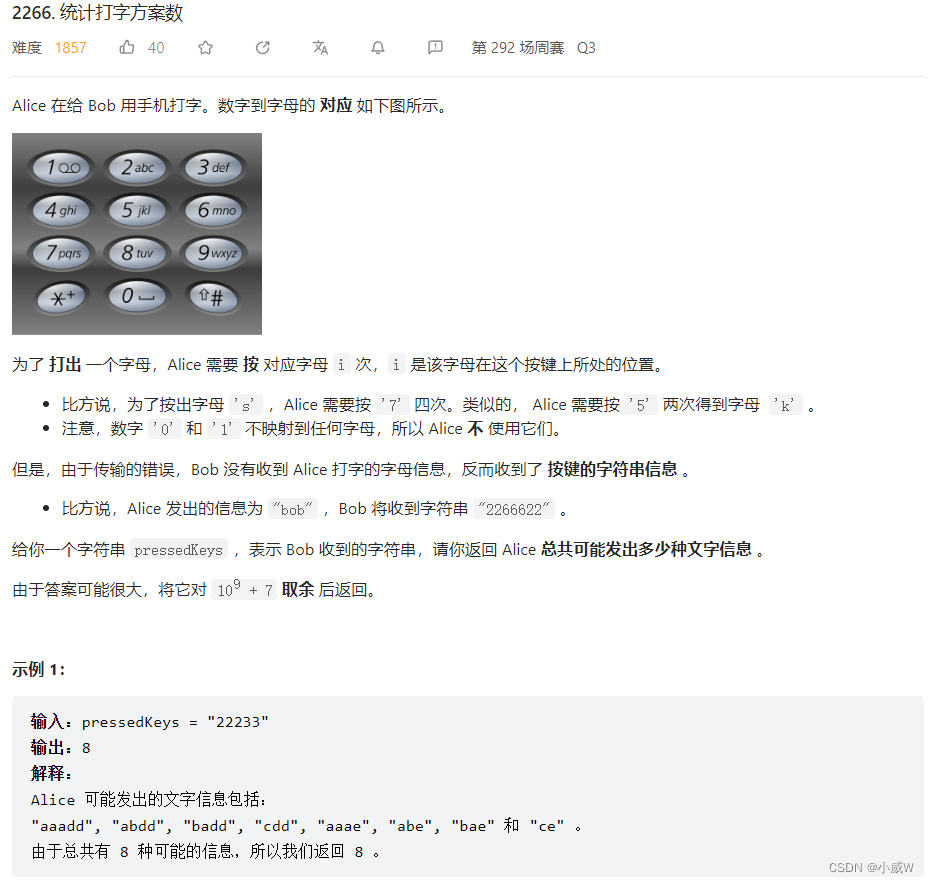
在这里插入图片描述

分组 + 线性DP + 乘法原理

把相同字符分为一组，每组内只有一种字符。

计算各组可能的方案，最后将各组方案相乘即可。

class Solution {
    final static int N = (int)1e5;
    final static long mod = (int)1e9 + 7;
    static long[] dp1 = new long[N], dp2 = new long[N];

    static {
        dp1[0] = dp2[0] = 1;
        dp1[1] = dp2[1] = 2;
        dp1[2] = dp2[2] = 4;
        dp1[3]= 7;
        dp2[3] = 8;
        for (int i = 4; i < N; ++i) {
            dp1[i] = (dp1[i - 1] + dp1[i - 2] + dp1[i - 3]) % mod;
            dp2[i] = (dp2[i - 1] + dp2[i - 2] + dp2[i - 3] + dp2[i - 4]) % mod;
        }
    }

    public int countTexts(String pressedKeys) {
        int n = pressedKeys.length();
        long ans = 1;
        for (int l = 0, r = 0; l < n; ++l) {
            char ch = pressedKeys.charAt(l);
            while (r < n && pressedKeys.charAt(r) == ch) r++;
            int len = r - l;
            if (ch == '7' || ch == '9') ans = (ans * dp2[len - 1]) % mod;
            else ans = (ans * dp1[len - 1]) % mod;
            l = r - 1;
        }
        return (int)ans;
    }
}

2272. 最大波动的子字符串⭐⭐⭐⭐⭐

2272. 最大波动的子字符串

在这里插入图片描述
提示：
1 <= s.length <= 10^4
s 只包含小写英文字母。

思路——枚举最多和最少的字符+最大子数组和

从 26 个字母中选出 2 个字母，分别作为最大值和最小值，一共需要枚举 $A_{26}^{2} = 26 × 25 = 650$ 种不同的字母组合。

对于每种组合，操作类似求最大子数组和。（但是要求必须两种字母都要出现）。

在这里插入图片描述

代码

class Solution {
    public int largestVariance(String s) {
        int n = s.length(), ans = 0;
        for (char a = 'a'; a <= 'z'; ++a) {
            for (char b = 'a'; b <= 'z'; ++b) {
                if (a == b) continue;
                // diff维护a和b之差 diffWithB维护包含了b的a和b之差
                int diff = 0, diffWithB = -s.length();
                // a作为最大值 b作为最小值时的答案
                for (int i = 0; i < n; ++i) {
                    if (s.charAt(i) == a) {
                        ++diff;
                        ++diffWithB;
                    } else if (s.charAt(i) == b) {
                        diffWithB = --diff;
                        diff = Math.max(diff, 0);
                    }
                }
                ans = Math.max(ans, diffWithB);
            }
        }
        return ans;
    }
}

这里 diff 维护 a 和 b 之差， diffWithB 维护包含了 b 的 a 和 b 之差。

初始化时 diffWithB 设置成了一个很小的负值，所以就算跟着 diff 一直增加，如果 b 不出现的话，diffWithB 也不会更新成 --diff，也就不会影响答案的最大值了。

2305. 公平分发饼干（子集状态压缩DP）

2305. 公平分发饼干
在这里插入图片描述
提示：

2 <= cookies.length <= 8
1 <= cookies[i] <= 10^5
2 <= k <= cookies.length

解法1——dfs回溯+剪枝

看到数据范围很小只有 8，可以先尝试一下暴力一点的做法。
比如尝试每一种分配的情况，使用每一种情况的最大值更新当前的答案。

class Solution {
    int[] sum, cookies;
    int ans = Integer.MAX_VALUE, k;

    public int distributeCookies(int[] cookies, int k) {
        this.cookies = cookies;
        this.k = k;
        sum = new int[k];
        dfs(0);
        return ans;
    }

    public void dfs(int i) {
        if (i == cookies.length) {
            // 更新答案
            ans = Math.min(ans, Arrays.stream(sum).max().getAsInt());
            return;
        }   
        for (int j = 0; j < k; ++j) {
            if (sum[j] + cookies[i] >= ans) continue;   // 剪枝
            sum[j] += cookies[i];
            dfs(i + 1);
            sum[j] -= cookies[i];
        }
    }
}

但是如果真的是纯暴力的话还是会超时，因此加了一个剪枝，就是在枚举分配情况的过程中如果检测到当前的值已经大于答案 ans了，那么就没有必要再继续 dfs 下去了，因为它一定不会影响到答案了。

除此之外，还可以先对 cookies 排序，在回溯的过程中先放入比较大的饼干，这样更容易触发剪枝的条件。

解法2——子集状压DP⭐⭐⭐⭐⭐（很重要！值得一学）

dp数组的定义：
dp[i][j] 表示将集合 j 分成 i 个集合时，这些集合的元素和的最大值的最小值是多少。

dp数组的递推：
考虑 dp[i][j] 如何转移出来，
此时已经组成了 i 个集合，那么考虑它可以从 i - 1 个集合的形式中转移出来
即 dp[i][j] = Math.min(dp[i][j], Math.max(dp[i - 1][j ^ s], sum[s]))
这里的 Math.max(dp[i - 1][j ^ s], sum[s])) 即在求这种分集合的方式时，各个集合元素和的最大值。
而我们需要求的是各种分法中得出的这些最大值里面的最小值是多少。

class Solution {
    public int distributeCookies(int[] cookies, int k) {
        // 答案的顺序和输入的顺序无关
        // 有消耗的概念 集合的划分
        // 状压DP

        // f[i][j] 消耗了 k 个子序列，这些子序列组成了集合 j
        // 这 k 个子序列的元素和的最大值的最小值为 f[i][j]
        
        // f[i][j] = 枚举 j 的子集 s
        // min max(f[i - 1][j ^ s], sum[s]) for s in j

        int n = cookies.length;
        int[] sum = new int[1<<n];    // 记录各个子集的和
        for (int i = 1; i < 1<<n; ++i) {    // 枚举每个子集
            for (int j = 0; j < n; ++j) {   
            	// 检查这个子集中是否有cookies[j]
                if ((i >> j & 1) == 1) sum[i] += cookies[j];
            }
        }

        int[][] dp = new int[k][1<<n];
        dp[0] = sum;                    // 只消耗了一个序列 相当于它本身
        for (int i = 1; i < k; ++i) {   // 计算分成i个子序列的答案
            for (int mask = 1; mask < 1<<n; ++mask) {
                dp[i][mask] = 0x3f3f3f3f;
                // 枚举mask的所有子集
                for (int s = mask; s != 0; s = (s - 1) & mask) {    // &mask 保证了是mask的子集
                    dp[i][mask] = Math.min(dp[i][mask], Math.max(dp[i - 1][mask ^ s], sum[s]));    // 相当于分走了一个子集s给新的序列
                }
            }
        }
        // 表示k个子集组成了这个大子集
        return dp[k - 1][(1<<n) - 1];
    }
}

代码技巧——如何枚举一个集合的所有子集⭐🐂

在这道题目中是在枚举 mask 的所有子集 s。
代码体现为：

// &mask 保证了是mask的子集
for (int s = mask; s != 0; s = (s - 1) & mask) {    

}

令 s 从 mask 开始，不断减小，同时将其与 mask 进行 & 运算，使其保证是 mask 的一个子集。

这种方法可以保证 s 作为 mask 的子集 不重不漏。

代码的空间优化

由于 dp[i] 只会从 dp[i - 1] 转移过来，因此可以删去第一个维度。

同时倒着枚举 mask。

修改之后的代码如下：

class Solution {
    public int distributeCookies(int[] cookies, int k) {
        // 答案的顺序和输入的顺序无关
        // 有消耗的概念 集合的划分
        // 状压DP

        // f[i][j] 消耗了 k 个子序列，这些子序列组成了集合 j
        // 这 k 个子序列的元素和的最大值的最小值为 f[i][j]
        
        // f[i][j] = 枚举 j 的子集 s
        // min max(f[i - 1][j ^ s], sum[s]) for s in j

        int n = cookies.length;
        int[] sum = new int[1<<n];    // 记录各个子集的和
        for (int i = 1; i < 1<<n; ++i) {    // 枚举每个子集
            for (int j = 0; j < n; ++j) {   // 检查这个子集中是否有cookies[j]
                if ((i >> j & 1) == 1) sum[i] += cookies[j];
            }
        }

        int[] dp = Arrays.copyOf(sum, 1 << n);
        for (int i = 1; i < k; ++i) {   // 计算分成i个子序列的答案
            for (int mask = (1 << n) - 1; mask >= 1; --mask) {
                // 枚举mask的所有子集
                for (int s = mask; s != 0; s = (s - 1) & mask) {    // &mask 保证了是mask的子集
                    dp[mask] = Math.min(dp[mask], Math.max(dp[mask ^ s], sum[s]));    // 相当于分走了一个子集s给新的序列
                }
            }
        }
        // 表示k个子集组成了这个大子集
        return dp[(1<<n) - 1];
    }
}

至于为什么要倒着枚举 mask，是因为它会在更小的 mask 转移过来，所以我们不能在使用其之前先将其覆盖了。

补充：相似题目练习——1723. 完成所有工作的最短时间

https://leetcode.cn/problems/find-minimum-time-to-finish-all-jobs/
在这里插入图片描述

class Solution {
    public int minimumTimeRequired(int[] jobs, int k) {
        int n = jobs.length;
        // dp[i][j]表示将集合j分成i个子集时最小的最大花费
        int[][] dp = new int[k][1 << n];

        // 计算各个集合对应的工作时间和
        int[] sum = new int[1 << n];
        for (int i = 1; i < 1<<n; ++i) {
            for (int j = 0; j < n; ++j) {
                if ((i >> j & 1) == 1) sum[i] += jobs[j];
            }
        }

        dp[0] = sum;    // 就是原数组作为一个集合
        for (int i = 1; i < k; ++i) {   // 枚举子集合数量
            for (int j = 1; j < 1 << n; ++j) {
                dp[i][j] = 0x3f3f3f3f;
                for (int s = j; s != 0; s = (s - 1) & j) {
                    dp[i][j] = Math.min(dp[i][j], Math.max(dp[i - 1][j ^ s], sum[s]));
                }
            }
        }

        return dp[k - 1][(1<<n) - 1];
    }
}

可以说跟上面那道题目是一模一样。

2312. 卖木头块⭐⭐⭐

2312. 卖木头块
在这里插入图片描述

提示：
1 <= m, n <= 200
1 <= prices.length <= 2 * 10^4
prices[i].length == 3
1 <= hi <= m
1 <= wi <= n
1 <= pricei <= 10^6
所有 (hi, wi) 互不相同。

解法1——记忆化搜索

dp[i][j] 表示一个 i * j 的木块可以获得的最多钱数。

class Solution {
    long[][] dp;
    int[][] prices;
    Map<String, Integer> value = new HashMap();

    public long sellingWood(int m, int n, int[][] prices) {
        this.prices = prices;
        // dp[i][j] 表示一个 i * j 的木块可以获得的最多钱数
        dp = new long[m + 1][n + 1];
        for (int i = 0; i <= m; ++i) Arrays.fill(dp[i], -1);
        for (int[] p: prices) {
            value.put(p[0] + " " + p[1], p[2]);
        }
        return dfs(m, n);
    }

    public long dfs(int m, int n) {
        if (dp[m][n] != -1) return dp[m][n];
        long res = value.getOrDefault(m + " " + n, 0);
        for (int i = 1; i < m; ++i) res = Math.max(res, dfs(i, n) + dfs(m - i, n));
        for (int j = 1; j < n; ++j) res = Math.max(res, dfs(m, j) + dfs(m, n - j));
        return dp[m][n] = res;
    }
}

对于一块木头，我们可以选择横着将其切开或者竖着将其切开。

解法2——线性DP

使用 prices 对 dp 数组进行初始化。
由于 m 和 n 的数据范围是 200，因此可以使用三次循环。
关于数据范围可见：由数据范围反推算法复杂度以及算法内容

class Solution {
    public long sellingWood(int m, int n, int[][] prices) {
        long[][] dp = new long[m + 1][n + 1];
        for (int[] p: prices) dp[p[0]][p[1]] = p[2];
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                for (int k = 1; k < i; ++k) dp[i][j] = Math.max(dp[i][j], dp[i - k][j] + dp[k][j]);
                for (int k = 1; k < j; ++k) dp[i][j] = Math.max(dp[i][j], dp[i][j - k] + dp[i][k]);
            }
        }
        return dp[m][n];
    }
}

2318. 不同骰子序列的数目

2318. 不同骰子序列的数目
在这里插入图片描述
提示：
1 <= n <= 10^4

解法1——三维DP

代码写起来很长，但是思路很清晰。

注意好 dp 数组的定义：
dp[i][j][k] 表示长度为 i，最后一个数字是 j ，倒数第二个数字是 k 的不同的序列个数。

其中当前数字和上一个数字不能相同且最大公约数是 1，当前数字和倒数第二个数字不能相同。

class Solution {
    static final int MOD = (int)1e9 + 7, MX = (int)1e4 + 1;
    static int[][][] dp = new int[MX][6][6];

    static {
        for (int i = 0; i < 6; ++i) {
            for (int j = 0; j < 6; ++j) {
                if (j != i && gcd(i + 1, j + 1) == 1) dp[2][i][j] = 1;
            }
        }

        for (int i = 3; i < MX; ++i) {             	// 枚举每个长度
            for (int j = 0; j < 6; ++j) {           // 枚举当前数字
                for (int k = 0; k < 6; ++k) {       // 枚举上一个数字
                    if (k != j && gcd(k + 1, j + 1) == 1) {     
                        for (int last = 0; last < 6; ++last) {    // 枚举上上个数字
                            if (last != j) {
                                dp[i][j][k] = (dp[i - 1][k][last] + dp[i][j][k]) % MOD;
                            }
                        }
                    }
                }
            }
        }
    }

    public int distinctSequences(int n) {
        if (n == 1) return 6;
        int ans = 0;
        for (int i = 0; i < 6; ++i) {
            for (int j = 0; j < 6; ++j) {
                ans = (ans + dp[n][i][j]) % MOD;
            }
        }
        return ans;
    }

    static int gcd(int a, int b) {
        return b == 0? a: gcd(b, a % b);
    }
}

解法2——二维DP⭐

TODO

在这里插入代码片

2320. 统计放置房子的方式数

2320. 统计放置房子的方式数
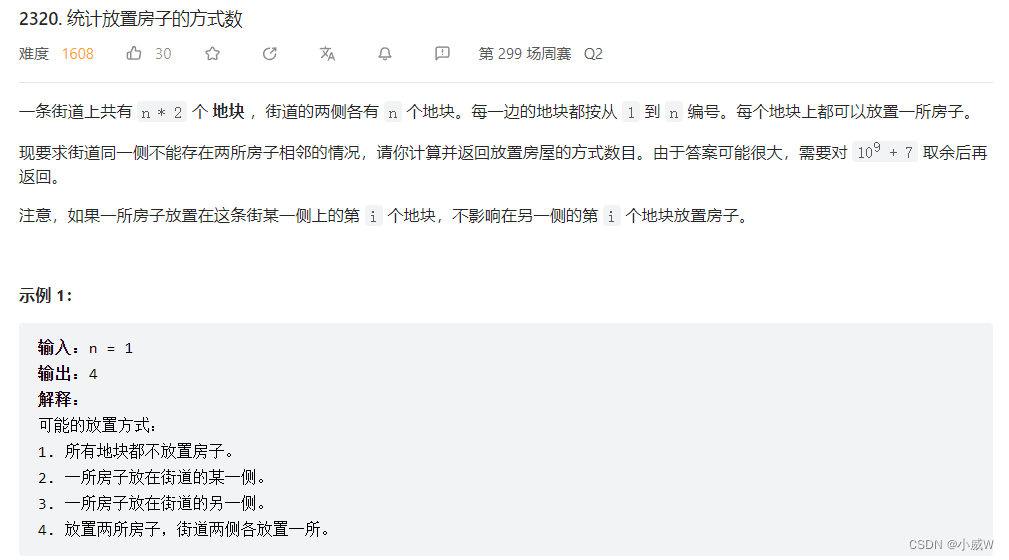
在这里插入图片描述
街道两侧的 dp 情况相同而又互不影响，只需计算其中一侧，最后结果是两边方案数的乘积。

代码1

class Solution {
    public int countHousePlacements(int n) {
        long[][] dp = new long[n][2];
        final long mod = (long)1e9 + 7;
        dp[0][0] = dp[0][1] = 1;
        for (int i = 1; i < n; ++i) {
        	// 这块不放，所以上块可以放也可以不放
            dp[i][0] = (dp[i - 1][0] + dp[i - 1][1]) % mod;
            // 这块放，所以上块不能放
            dp[i][1] = dp[i - 1][0];
        }
        long s = dp[n - 1][0] + dp[n - 1][1];
        return (int)(s * s % mod);
    }
}

代码2——变量代替dp数组

class Solution {
    public int countHousePlacements(int n) {
        long a = 1, b = 1;
        final long mod = (long)1e9 + 7;
        for (int i = 1; i < n; ++i) {
            long t = a;
            a = (a + b) % mod;
            b = t;
        }
        long s = a + b;
        return (int)(s * s % mod);
    }
}

代码3——static代码块预处理

class Solution {
    static final int mod = (int)1e9 + 7, N = (int)1e4 + 1;
    static final int[] dp = new int[N];

    static {
        dp[0] = 1;
        dp[1] = 2;
        for (int i = 2; i < N; ++i) dp[i] = (dp[i - 1] + dp[i - 2]) % mod;
    }

    public int countHousePlacements(int n) {
        return (int)((long)dp[n] * dp[n] % mod);
    }
}

2321. 拼接数组的最大分数

2321. 拼接数组的最大分数
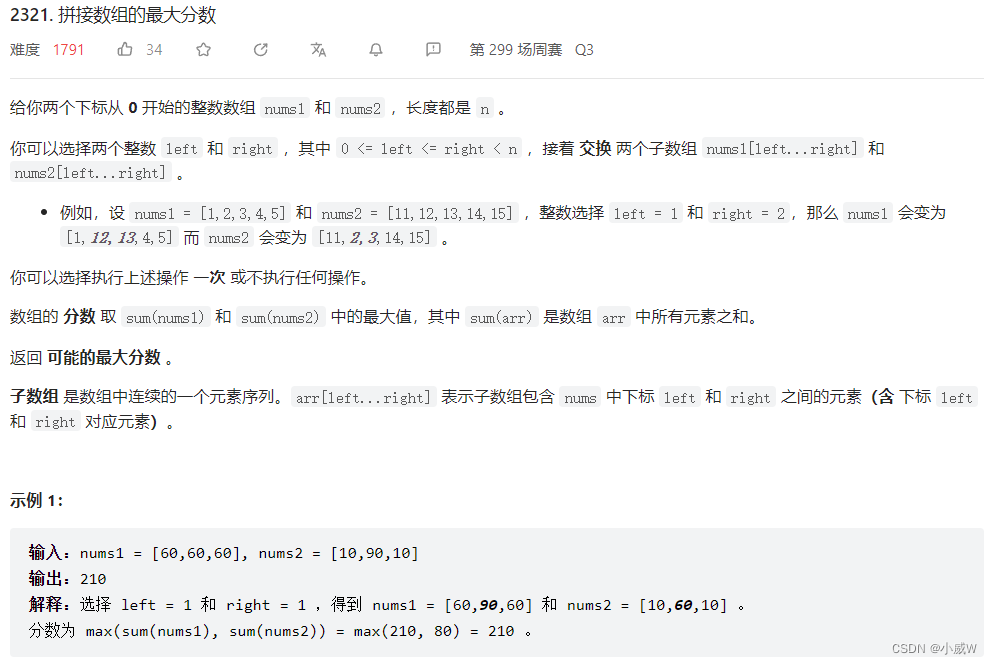
在这里插入图片描述

转换成最大子数组和

转换成 53. 最大子数组和。
即计算两数组的差分数组的最大子数组和，即可找到可以选择的最佳 left 和 right 下标。

class Solution {
    public int maximumsSplicedArray(int[] nums1, int[] nums2) {
        int a = Arrays.stream(nums1).sum(), b = Arrays.stream(nums2).sum();
        return Math.max(a + op(nums1, nums2), b + op(nums2, nums1));
    }
	
	// op(a, b) 计算 b里面大的数字交给a
    public int op(int[] nums1, int[] nums2) {
        int ans = 0, n = nums1.length, sum = 0;
        for (int i = 0; i < n; ++i) {
            sum += nums2[i] - nums1[i];
            if (sum < 0) sum = 0;
            else ans = Math.max(ans, sum);
        }
        return ans;
    }
}

注意有可能是 1 换给 2 ，也有可能是 2 中大的元素换给 1。

LCP 53. 守护太空城（子集状压DP）⭐⭐⭐⭐⭐🚹🚹🚹🚹🚹

LCP 53. 守护太空城
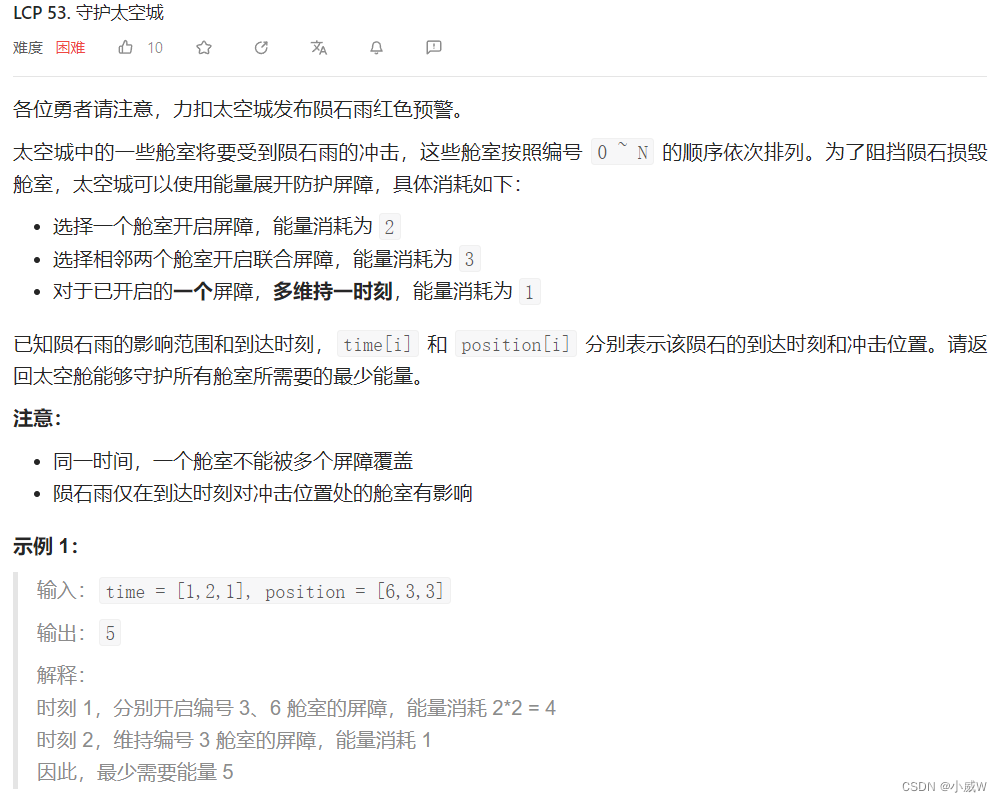
在这里插入图片描述
https://leetcode.cn/problems/EJvmW4/solutions/1426981/by-endlesscheng-pk2q/

定义 dp[i][j] 表示考虑前 i 个舱室，且第 i 个舱室与第 i + 1 个舱室开启联合屏障的时间点集合为 j 时，所需的最小能量。

我们使用 union[i] 和 single[i] 分别记录开启联合/单独屏障的时间点集合恰好为 i 时，所需要的最少能量。

对于位置 0 ，联合保护罩的开启时间集合是 j ，则它的最小消耗就是 union[j] + single[((m - 1) ^ j) & rain[0]]。（即除去联合时间外，剩下且下雨的时间集合）

dp[i][j] 从 dp[i - 1][pre] 转移过来，其中 pre 是枚举 j 的补集。

class Solution {
    public int defendSpaceCity(int[] time, int[] position) {
        int n = Arrays.stream(position).max().getAsInt();
        int m = 1 << Arrays.stream(time).max().getAsInt();
        int[] rain = new int[n + 1];    // 记录每个位置下雨的时刻
        for (int i = 0; i < time.length; ++i) {
            rain[position[i]] |= 1 << (time[i] - 1);
        }

        // union和single分别表示开启时间点为j时所需的最小能量
        int[] union = new int[m], single = new int[m];
        for (int i = 1; i < m; ++i) {
            // j是去掉二进制最后一个1的i
            int lb = i & -i, j = i ^ lb, lb2 = j & -j;
            union[i] = union[j] + (lb == (lb2 >> 1)? 1: 3); // 检查i和j是否时间点相邻
            single[i] = single[j] + (lb == (lb2 >> 1)? 1: 2);
        }

        // dp[i][j] 表示考虑前 i 个舱室，且第 i 个舱室与第 i + 1 个舱室开启联合屏障的时间点集合为 j 时，所需的最小能量。
        int[][] dp = new int[n + 1][m];
        for (int j = 0; j < m; ++j) {
            dp[0][j] = union[j] + single[((m - 1) ^ j) & rain[0]];
        }
        for (int i = 1; i <= n; ++i) {
            Arrays.fill(dp[i], Integer.MAX_VALUE / 2);
            for (int j = 0; j < m; ++j) {	// 枚举位置i在时间集合j开启联合保护罩
                // 枚举 j 的补集 mask 中的子集 pre (即与j不重叠的所有其它时间集合pre)
                for (int mask = (m - 1) ^ j, pre = mask; ; pre = (pre - 1) & mask) {
                    int cost = dp[i - 1][pre] + union[j] + single[(mask ^ pre) & rain[i]];
                    dp[i][j] = Math.min(dp[i][j], cost);
                    if (pre == 0) break;	// 注意必须写在这里,不能在if里写pre != 0
                }
            }
        }
        return dp[n][0];
    }
}