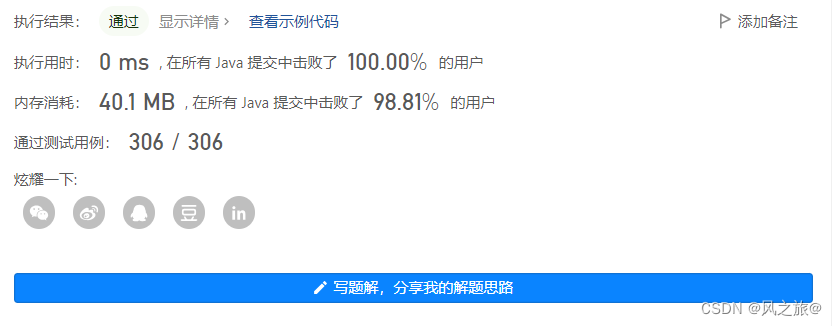
题目链接：力扣
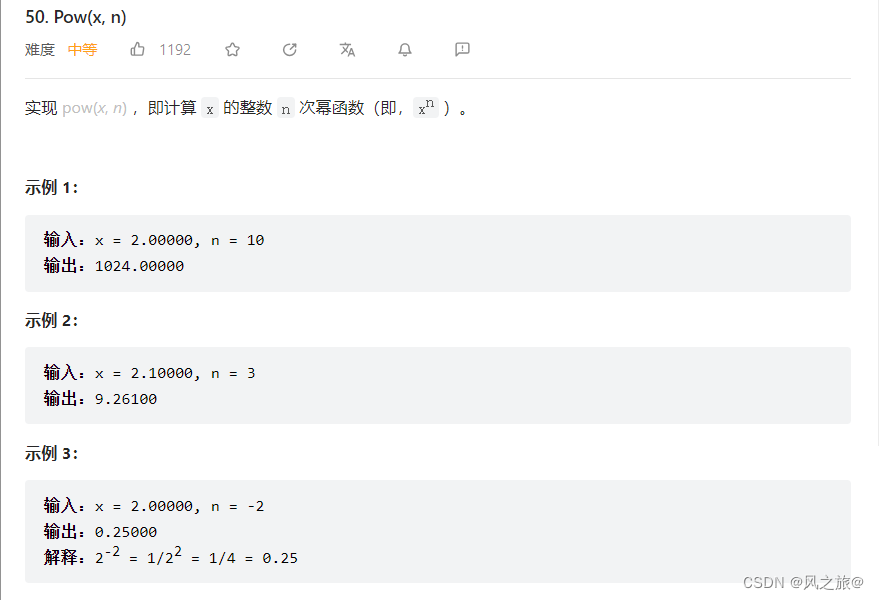解题思路：直接使用for进行累乘会超时（时间复杂度O(n)，n为指数n的大小），可以使用快速幂进行更快的幂运算(时间复杂度为O(logn))
快速幂：核心思想就是每一次把指数缩小一半，底数平方。对于a^n（a为底数，n为指数）
- 当n为偶数时，比如：a^10 = a^(2*5) = (a^2)^5，指数10缩小一般变为5，将底数a平方变为a^2（这个时候如果使用for循环求幂运算，只需要对a^2做5次累乘就可以了，相比10次累乘减少了一半的运算量）
- 当n为奇数时，比如：a^11，这个时候指数11缩小一半为5.5，但是指数不能为小数，可以先提取出一个底数a，a^11=a * a^10，然后对a^10进行指数缩小一半，底数平方的操作。
- 重复1和2，直到指数n为0
在上述过程中当指数为奇数时，都会分离出一个底数，最终指数一定会变为1，这个时候结果为b^1, 此时n为奇数，提取出一个底数b，b^1=b * b^0，提取后n=0，算法结束。可见，只需要每次在指数为奇数的时候，把提取出来的底数累乘到最终结果result上（n为偶数时不进行累乘），当n=0时，result即为所求。
比如2^11，按照上述算法流程，初始时result=1：
- 2^11，n为奇数，2^11=2 * 2^10，将提取出的底数累乘到result上，result=1*2=2，然后对2^10进行上述操作
- 2^10，n为偶数，2^10 = (2^2)^5=4^5，然后对4^5进行上述操作
- 4^5，n为奇数，4^5=4 * 4^4，将提取出来的底数累乘到result上，result = 2*4=8，然后对4^4进行上述操作
- 4^4，n为偶数，4^4 = (4^2)^2=16^2，然后对16^2进行上述操作
- 16^2，n为偶数，16^2 = (16^2)^1=256^1，然后对256^1进行上述操作
- 256^1，n为奇数，256^1 = 256 * 256^0，将提取出来的底数累乘到result上，result=8*256=2048，然后对256^0进行上述操作
- 256^0，n=0，算法结束，result=2048=2^11
由上述过程可见，只需要在n为奇数的时候，将提取出了的底数累乘到result上
快速幂代码
public static long quickPower(int base, int power) {
long result = 1;
while (power > 0) {
if (power%2==0){//如果指数为偶数
power = power /2 ;//把指数缩小为一半
base = base * base;//把底数变大为原来的平方
}else {//如果指数为奇数
power = power-1;//把指数减去1，使其变为一个偶数
result = result * base;//需要把提取出来的底数记录到结果中
power=power/2; //减1后，指数为偶数，可以继续进行指数缩小为一半
base = base *base; //底数变为原来的平方
}
}
return result;
}上述if和else代码中有重复性的代码，可以进行简化
n为偶数时
power = power /2;n为奇数时
power = power-1;
power=power/2;其实n为奇数时的这两行代码可以合并为一句
power = power /2;因为当n为奇数时，power/2 = (power-1)/2，因为在整形运算中，是向下取整的，比如(5-1)/2=5/2=4
简化后的快速幂算法：
public static long quickPower(int base, int power) {
long result = 1;
while (power != 0) {
if (power % 2 == 1) {
result = result * base;//需要把提取出来的底数记录到结果中
}
power = power / 2;//把指数缩小为一半
base = base * base;//把底数变大为原来的平方
}
return result;
}上述代码已经很简洁了，但是还可以进行优化，在计算机中位运算要比普通的加减乘除运算更快
power%2==1可以使用位运算代替，power为奇数时，二进制位的最后一位一定为1，如果最后一位不为1，则power为偶数，所以可以使用 power&1 得到power的最后一位。
power = power/2也可以替换为 power >>=1 的位运算
最终的快速幂算法实现：
public static long quickPower(int base, int power) {
long result = 1;
while (power != 0) {
if ((power & 1) == 1) {
result = result * base;//需要把提取出来的底数记录到结果中
}
power >>= 1;//把指数缩小为一半
base = base * base;//把底数变大为原来的平方
}
return result;
}明白了上述快速幂过程，这道题也就容易做了，因为n可能为负数，可以在n小于0时，令x=1/x，n=-n，这个时候就可以转化为正数的快速幂算法了，注意，转为正数时可能会发生整数溢出（当n为整数的最小值时），需要使用long类型保存n，然后对long类型进行负数转整数操作.
AC代码：
class Solution {
public static double myPow(double x, int n) {
double result = 1;
//防止溢出
long N = n;
if (N < 0) {
N = -N;
x = 1 / x;
}
while (N != 0) {
if ((N & 1) == 1) {
result = result * x;
}
x *= x;
N >>= 1;
}
return result;
}
}
