一、排序的概念

排序的概念

排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。

排序的稳定性

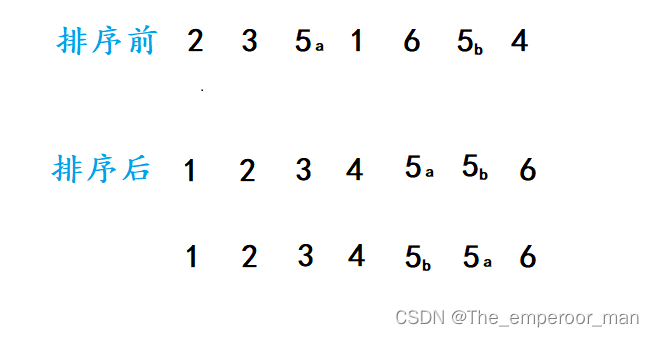
上述待排序的数中，有两个5。将前面的5标记一个a，将后面的5标记一个b。

通过算法进行排序后，这一组数就有序了，但是要看两个相同的5的位置是否有改变。
5a仍在5b前面，那么这个排序算法就是稳定的，
5a跑到了5b后面，那么这个排序算法就是不稳定的。
一个稳定的排序算法可以做到不稳定，
不稳定的排序算法一定做不到稳定。

至于为什么要讨论这个稳定性，是为了以后应用到实际场景上。比如，一场数学考试，假设a用了30分钟做完了，并得了满分。
假设b用了一个小时做完了，并得了满分。此时a与b都是得了满分，但是用的时间不一样，所以两个人的排名又会有所不同。

七大排序算法

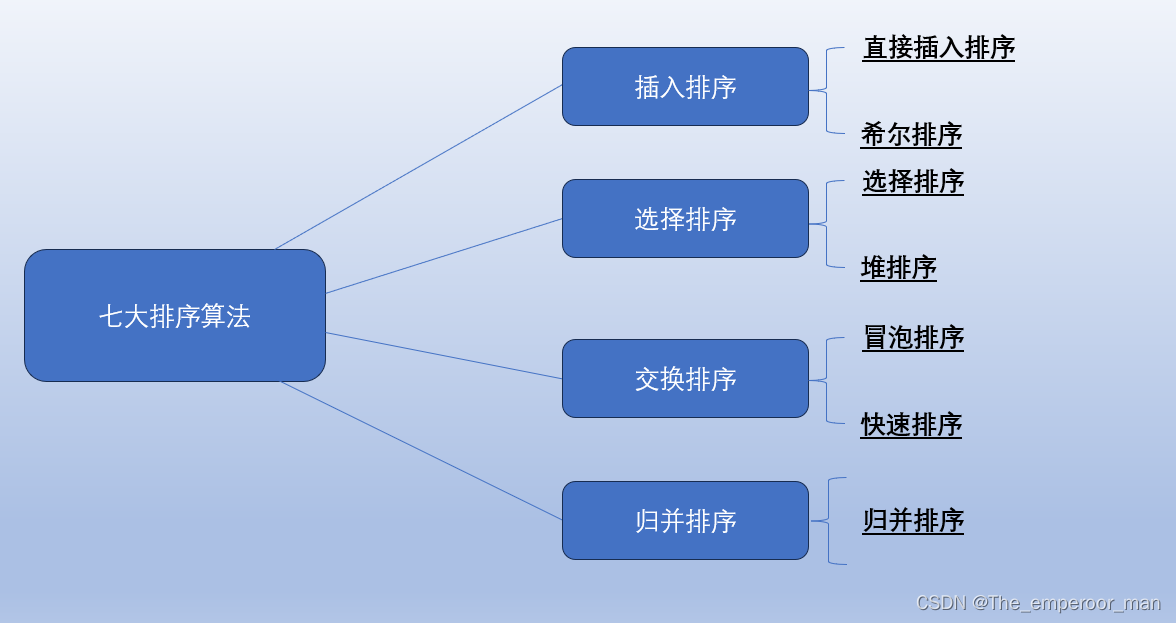
在这里插入图片描述

二、希尔排序

核心思想

基本思想： 希尔排序法又称缩小增量法。希尔排序法的基本思想是：

先选定一个整数，把待排序文件中所有记录分成多个组。
所有距离为的记录分在同一组内，并对每一组内的记录进行直接插入排序。
然后，取，重复上述分组和排序的工作。
当到达=1时，所有记录在统一组内排好序。

图解

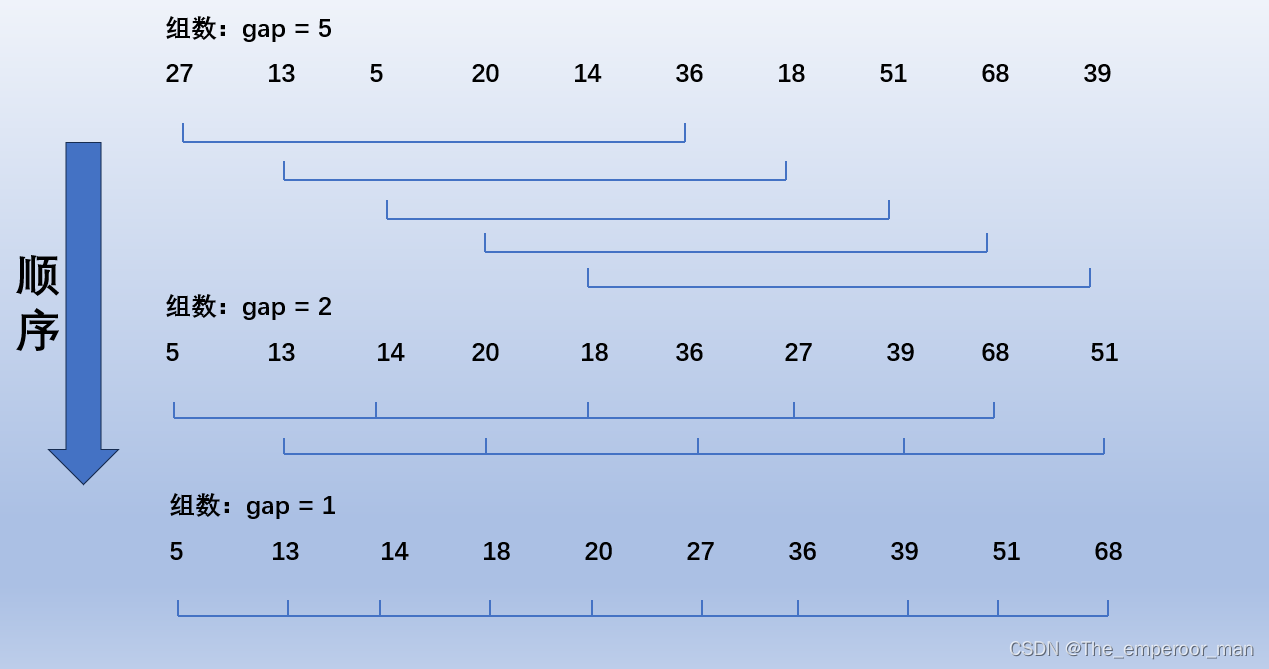
有一组待排序数列，我们进行升序排序。
排序过程：
说白了就是，将这些数分为几个组，这几个组再分别直接插入排序，然后分的组数减少，重复上述过程，直到只剩1组时，再对这个组排序，就完成了排序。

组数多则每组的数据少，组数少则每组的数据多。

代码实现

代码实现

public class ShellSort {
    /**
     * 希尔排序
     * 时间复杂度：O（n^1.3） - O(n^1.5)
     * 空间复杂度：O(1)
     * 稳定性：不稳定
     * @param array
     */
    public static void shell(int[] array) {
        // 组数
        int gap = array.length;
        while (gap > 1) {
            // gap组数变换比较随意，
            // gap /= 3;也可以
            gap /= 2;
            shell(array,gap);
        }
        // 最后让组数为1再排序一次
        shell(array,1);
    }
    public static void shell(int[] array,int gap) {
        for (int i = gap; i < array.length; i++) {
            // 默认每组内第一个数据都是有序的，
            // 从每组的第二个数据开始进行直接插入排序
            // i++即是跳到下一组，
            // 每组排序一个数，然后跳到下一组，如此循环。
            int tmp = array[i];
            int j = i - gap;
            
            // 跳跃式的组内直接插入排序
            for (; j >= 0 ; j-=gap) {
                if(array[j] > tmp) {
                    array[j+gap] = array[j];
                } else {
                    break;
                }
            }
            array[j + gap] = tmp;
        }
    }
}

三、性能分析

希尔排序的特性总结：
希尔排序是对直接插入排序的优化。直接插入排序的特定就是数据越有序，速度越快。

当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。

时间复杂度：
希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，因此在好些树中给出的希尔排序的时间复杂度都不固定：有学者通过大量的试验统计，得出结果为：O(n^1.25) - O(1.6*n^1.25)

空间复杂度：O(1)

稳定性：
不相邻的元素也会进行位置交换，是不稳定。