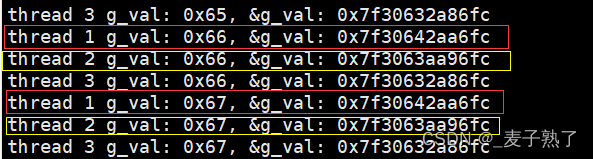
3.1 设置问题

根据图片的尺寸，把图片分为纵向图像和横向图像。这种把图像分成两种类别的问题，就是二分类问题。

纵向图片示例：
 

 横向图片示例：

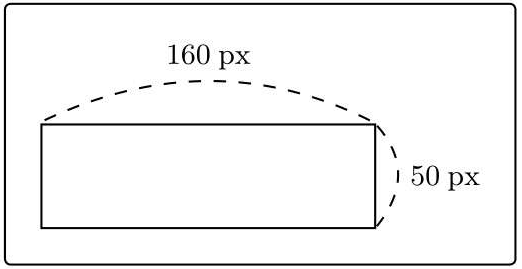
 这样就有了两个训练数据：

 增加训练数据，并在图像中表示出来：

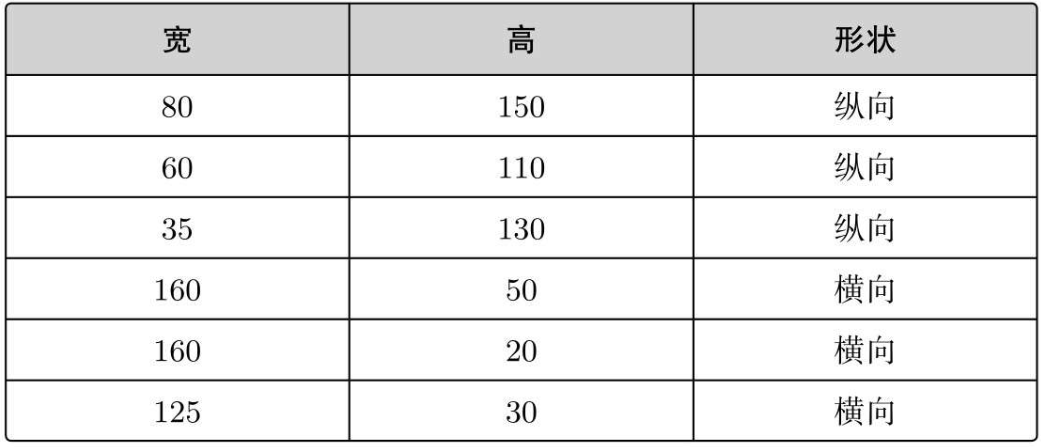
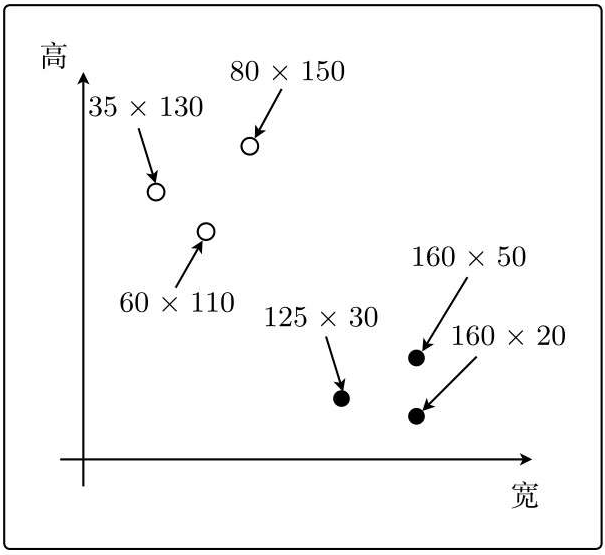
 可以得到一条分隔两边的线，这次分类的目的就是找到这条线：
 

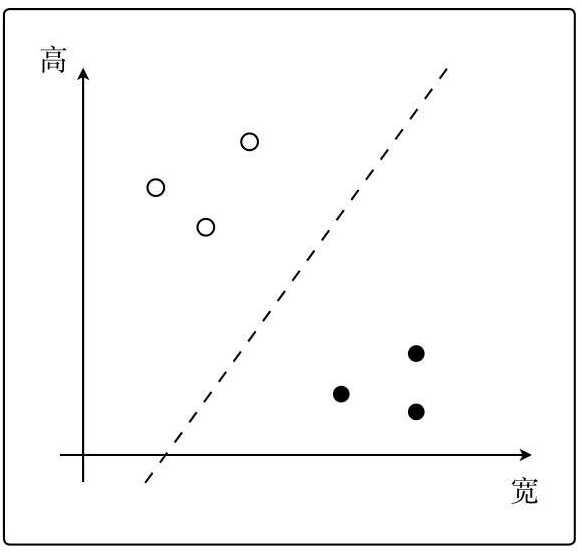
 只要找到这条线，就可以根据点在线的哪一边来判断图像是横向的还是纵向的了。

3.2 内积

上面图中的直线像学习回归时的一次函数一样，但是这次我们不是求斜率与截距了，而是找向量了。

图中的虚线，是使权重向量成为法线向量的直线。

设权重向量为w ,那么那条直线的表达式就是这样的：

 实向量空间的内积是各元素乘积的和，表达式也可以写成：

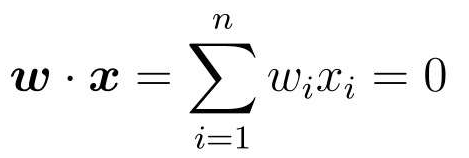
 法线是与某条直线相垂直的向量。现在我们假设权重向量w = (1,1)，代入表达式中可得：

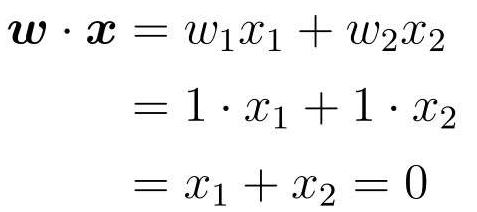
 在图中表示：

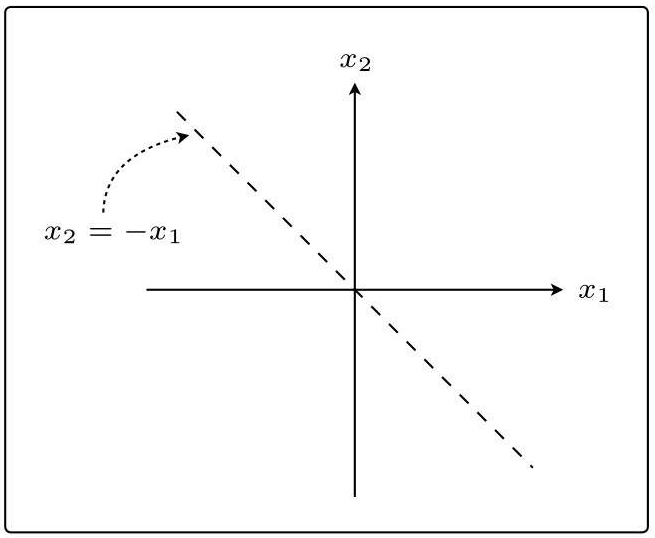
 然后再把权重向量加上：

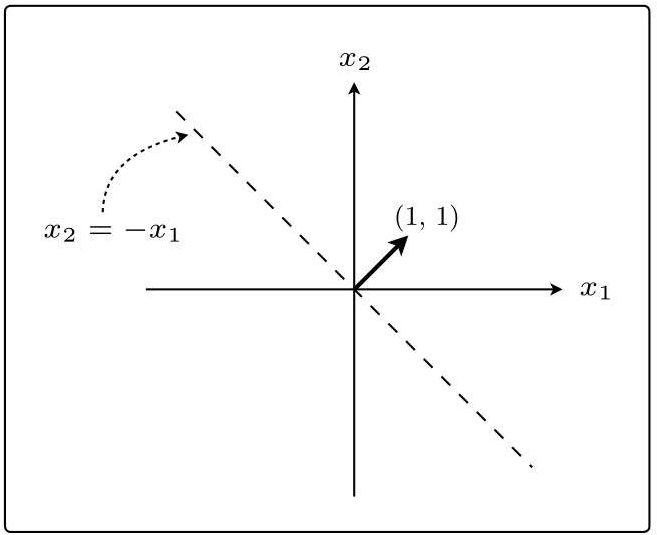
 回到刚开始，一开始并不存在画的那条虚线，我们要先通过训练找到权重向量，最后才能得到与这个向量垂直的直线，最后根据这条直线就可以对数据进行分类了。

3.3 感知机

那么具体要怎么求出权重向量呢？

基本的做法和回归时相同，就是将权重向量用作参数，创建更新表达式来更新参数。

感知机模型（perceptron）

接受多个输入后将每个值与各自的权重相乘，最后输出总和的模型：

 先准备一些训练数据。设表示宽的轴为x1，表示高的轴为x2，用y来表示图像是横向还是纵向的，横向的值为1，纵向的值为-1。

 根据参数向量x来判断图像是横向还是纵向的函数，即返回1或者-1的函数fw(x)的定义如下:

 这个被称为判别函数。

与权重向量w的内积为负的向量x是什么样的向量？

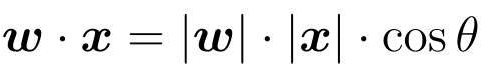
 因为|w|和|x|必定为正数，所以决定内积符号的是cos θ。

 cos θ的图：

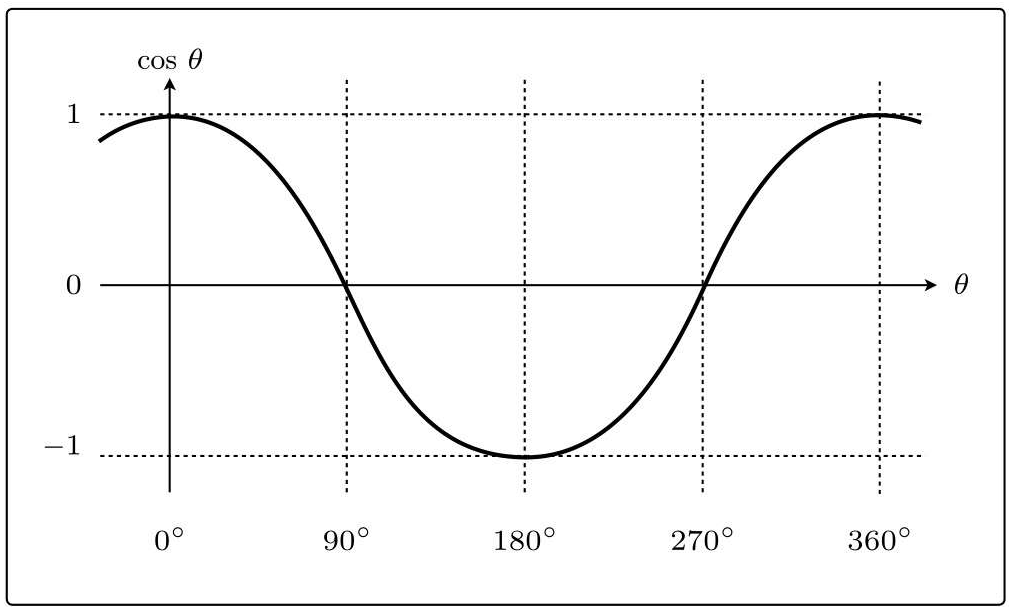
 在90◦＜θ＜270◦的时候cos θ为负。

在图中的体现：

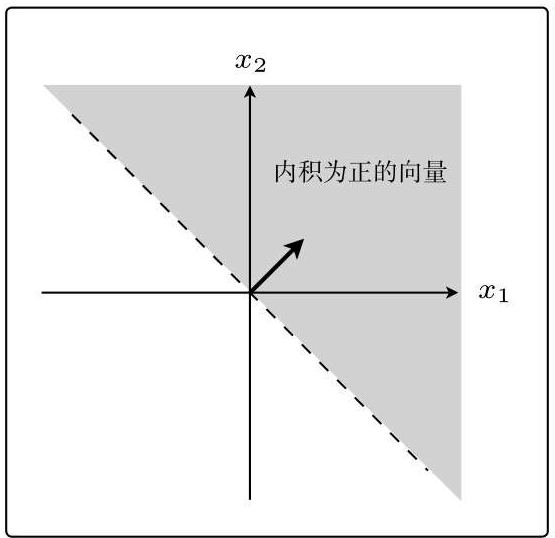
 积是衡量向量之间相似程度的指标。结果为正，说明二者相似；为0则二者垂直；为负则说明二者不相似。

根据上面的内容，可以推导出权重向量的更新表达式：

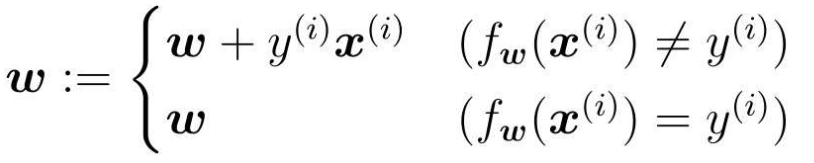
 通过判别函数对宽和高的向量x进行分类的结果与实际的标签y是否相同：

判别结果准确，fw(x(i))=y(i)，即分类成功，直接代入w。

判别结果失败，即分类失败，不能直接代入w。

更新示例：

先随意画一个权重向量：

 在这个状态下，假设第一个训练数据是x(1)=(125,30)：

 

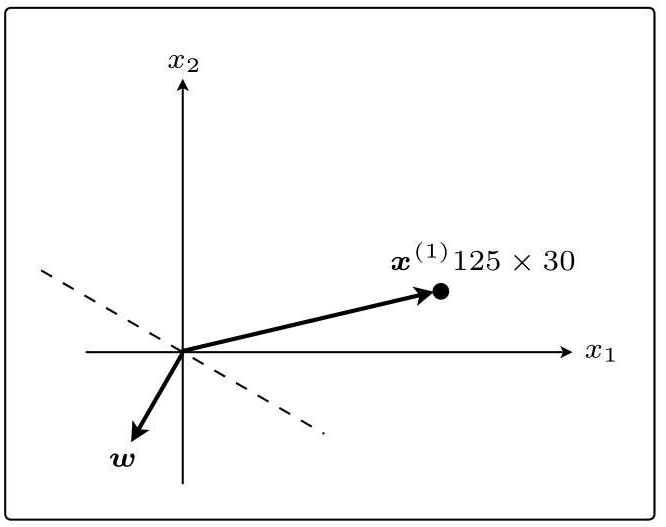
 w和x(1)之间的夹角θ的范围是90◦＜θ＜270◦，内积为负。也就是说，判别函数fw(x(1))的分类结果为-1，说明分类失败。

随后更新表达式：

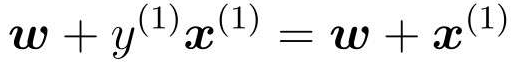
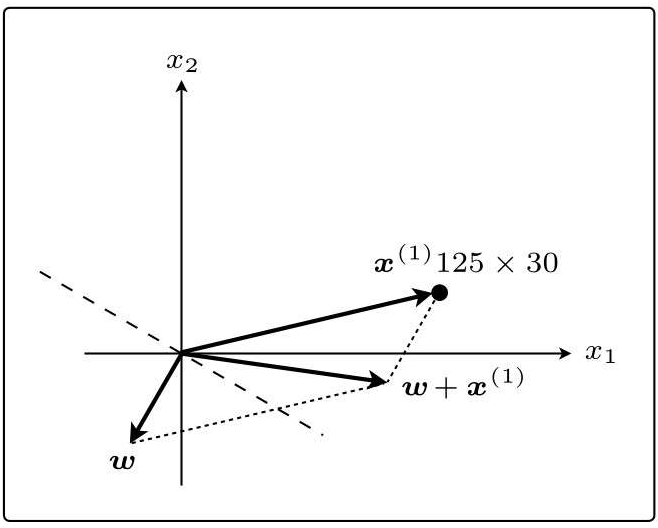
这个w+x(1)就是下一个新的w，画一条与新的权重向量垂直的直线，相当于把原来的线旋转了一下：

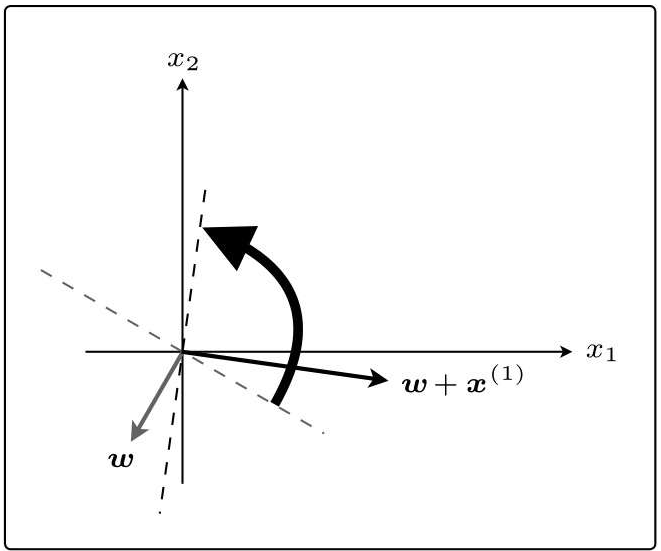
 刚才x(1)与权重向量分居直线两侧，现在它们在同一侧了：

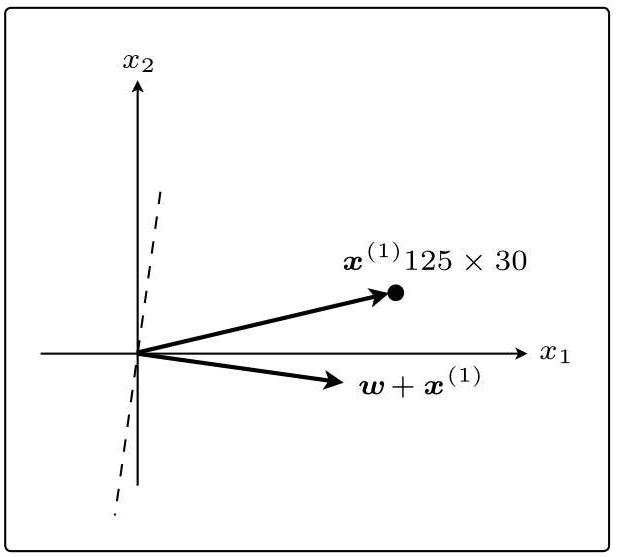
 这次θ＜90◦，所以内积为正，判别函数fw(x)的分类结果为1。而且x(1)的标签也为1，说明分类成功了。

这就是更新参数的权重向量。

3.4 线性可分

因为感知机只是简单的模型，他有一个很大的缺点，就是它只能解决线性可分的问题。

有下面这张图里的数据，其中圆点为1，叉号为-1，这样的图形无法用一条直线对这些数据进行分类。

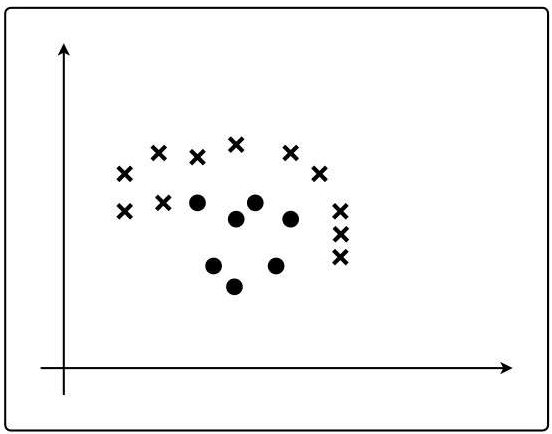
 这种感知机被称为简单感知机或单层感知机，实际上使用的神经网络是多层感知机。

3.5 逻辑回归

能应用于线性不可分问题的算法，这个算法与感知机的不同之处在于，它是把分类作为概率来考虑的。即图片为纵向的概率是，为横向的概率是，这里设横向的值为1、纵向的值为0。

需要能够将未知数据分类为某个类别的函数fθ(x)：

 这个函数的名字叫sigmoid函数：

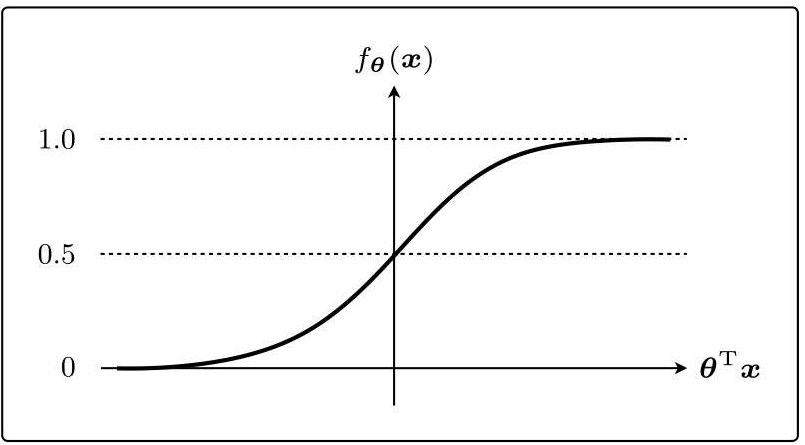
把未知数据x是横向图像的概率作为fθ(x)，表达式为：

P中的竖线是条件概率。

阈值为0.5，从而分类横向或纵向：

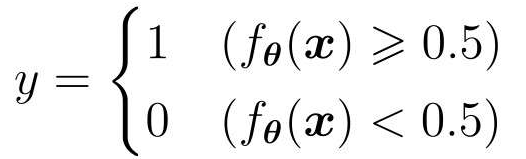
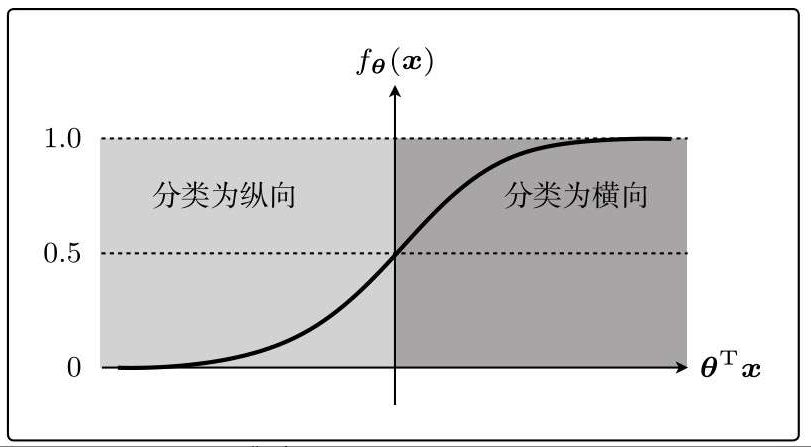
 表达式改写：

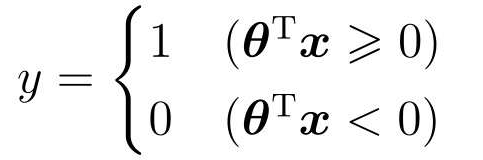
下面像学习感知机时那样，设横轴为图像的宽（x1）、纵轴为图像的高（x2）。

然后像学习回归时那样，先随便确定θ再具体地去考虑。比如当θ是这样的向量时，画一下θTx≥0的图像：

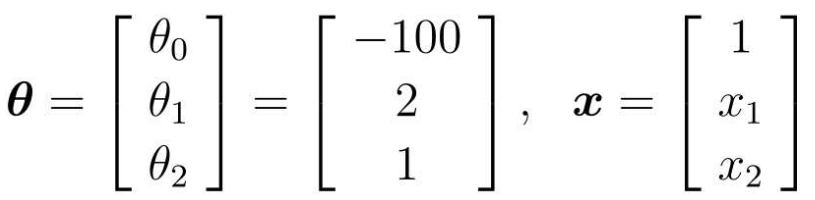
 代入数据：

 画出不等式对应的图：

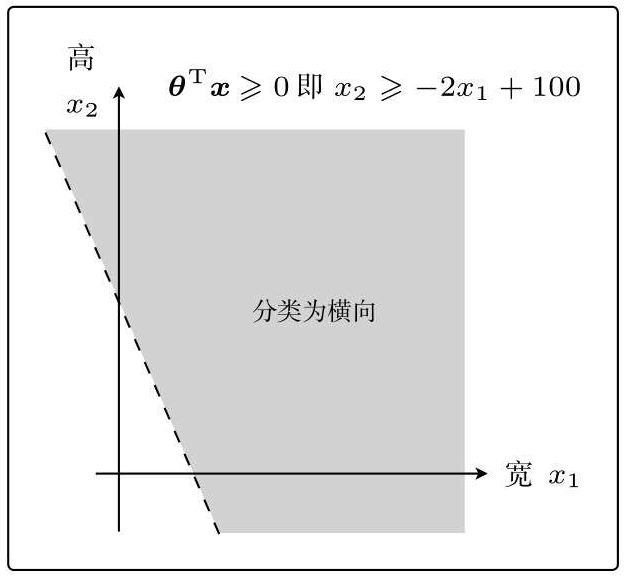
也就是说，我们将θTx=0这条直线作为边界线，就可以把这条线两侧的数据分类为横向和纵向了。

这种勇于数据分类的直线称为决策边界。

实际应用时这个决策边界并不能正确地分类图像，是因为我们刚开始决定参数的时候太随意了。

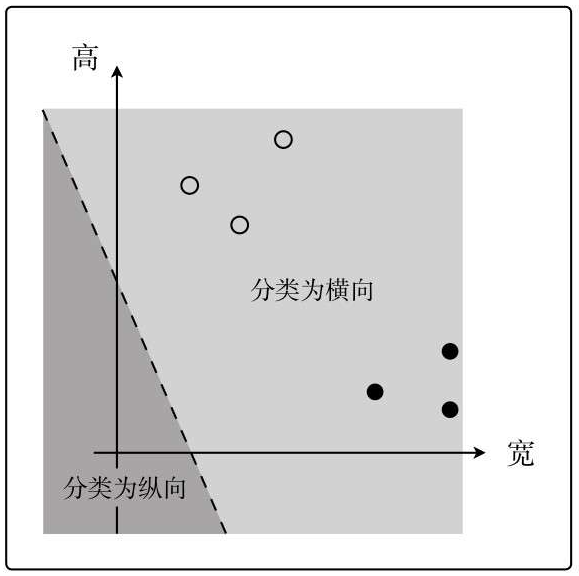
 为了求得正确的参数θ而定义目标函数，进行微分，然后求参数的更新表达式。这种算法就称为逻辑回归。

3.6 似然函数

现在来求参数的更新表达式。

首先要明确，既然fθ(x)是x为横向时的概率，那么在y=1时fθ(x)=1, y=0时fθ(x)=0的关系就是理想的。

简单来说：

- y = 1的时候，我们希望概率P（y = 1 | x）是最大的。

- y = 0的时候，我们希望概率P（y = 0 | x）是最大的。

作用在训练数据上：

假定所有的训练数据都是互不影响、独立发生的，这种情况下整体的概率就可以用下面的连个概率来表示：

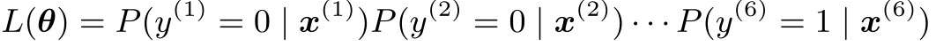
想一想扔2次骰子的情况。第1次的结果是1点，且第2次的结果是2点的概率是多少呢？首先1点出现的概率是1/6，接下来2点出现的概率是1/6，二者连续发生的概率就要使用乘法计算，其表达式是这样的：

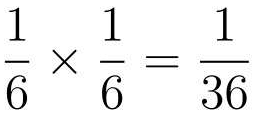
同理，第1次的概率是P(y(1)=0|x(1))，第2次的概率是P(y(2)=0|x(2))……我们要计算的是连续发生6次的概率。

联合概率的表达式一般化：

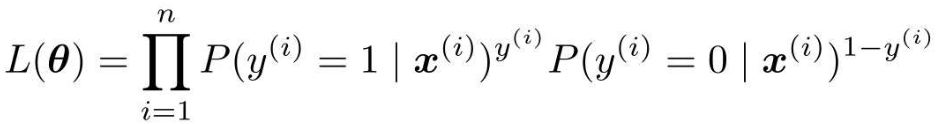
 分开考虑，首先向指数y(i)代入1：

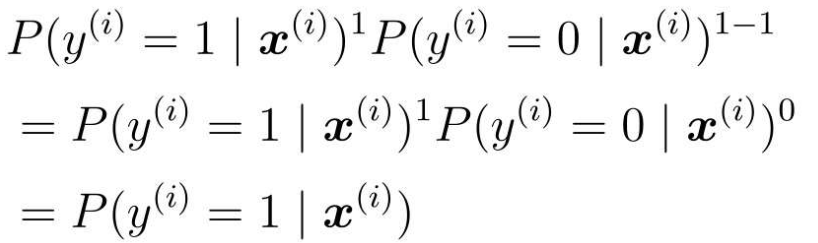
 再代入y(i)代入0：

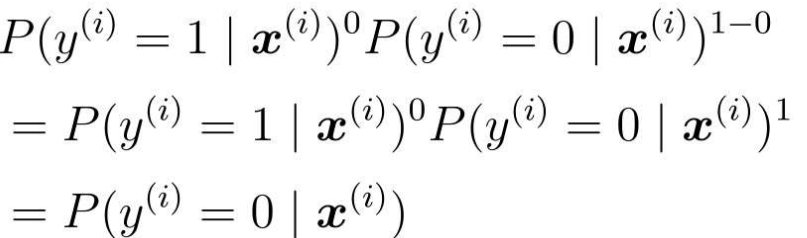
这就是它的目标函数，接下来考虑的是使这个目标函数最大化的参数θ。

回归的时候处理的是误差，所以要最小化，而现在考虑的是联合概率，我们希望尽可能大。

这里的目标函数L(θ)也被称为似然，函数的名字L取自似然的英文单词Likelihood的首字母。

3.7 对数似然函数

下面就是对似然函数进行微分，求出参数θ。

但是，直接对似然函数进行微分有点困难，在此之前要把函数变形，取似然函数的对数，两边加上log即可，如下：

 然后把对数似然函数进行变形：

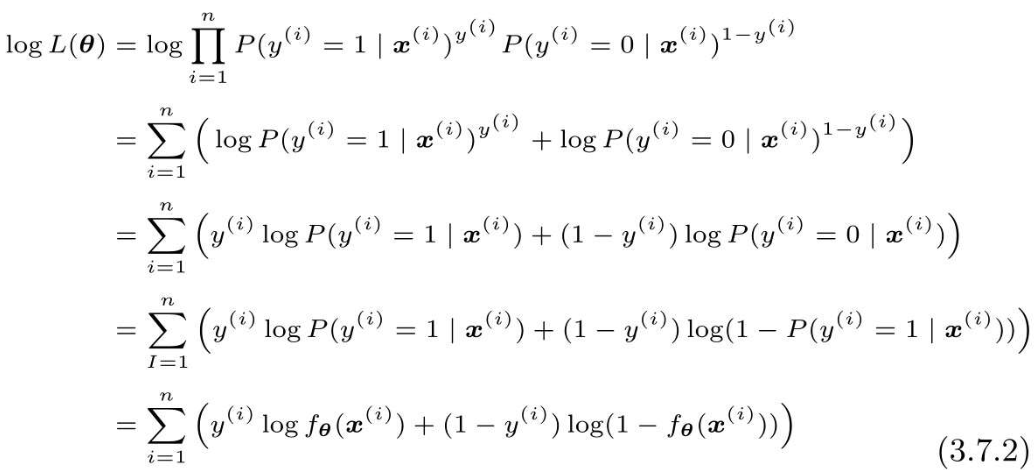
 最后，逻辑回归就是将这个对数似然函数用作目标函数：

 接下来，对各个参数θj求微分：

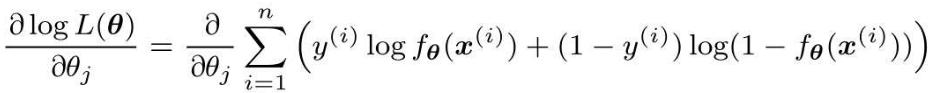
 和回归的时候是一样的，我们把似然函数也换成这样的复合函数，然后依次求微分：

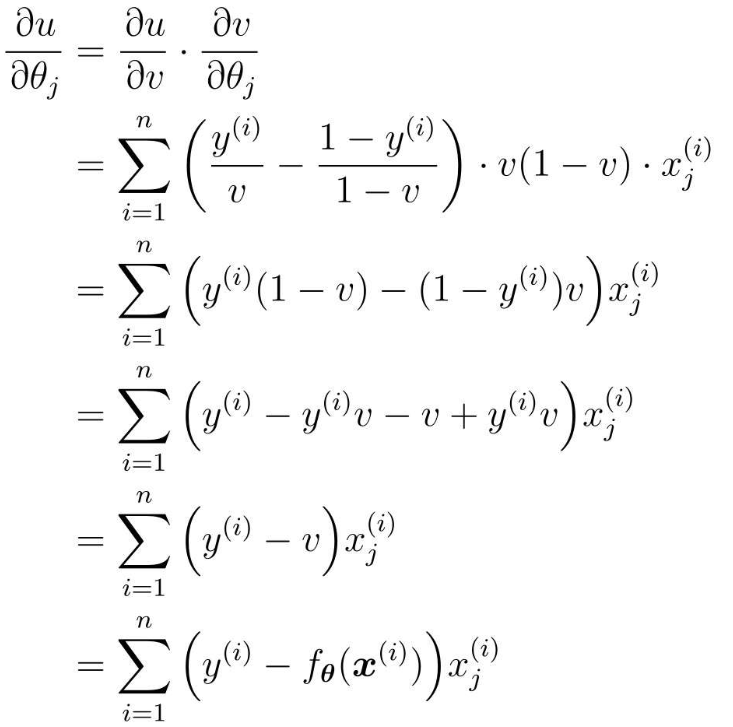
不过现在是以最大化为目标，所以必须按照与最小化时相反的方向移动参数：

 为了与回归时的符号保持一致，也可以将表达式调整为下面这样：

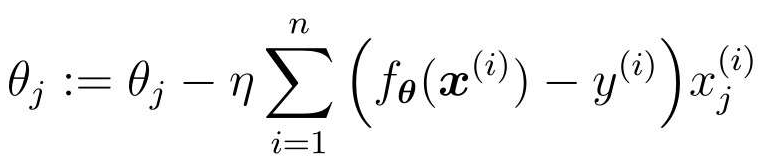
3.8 线性不可分

逻辑回归应用于线性不可分问题。

下面的图像是线性不可分的：

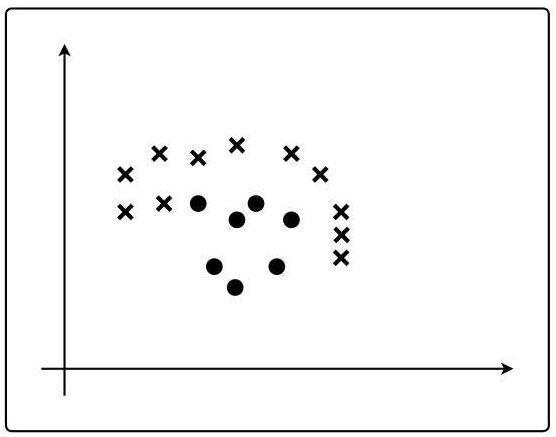
 对于这个问题，虽然直线不能分类，但是曲线可以分类：

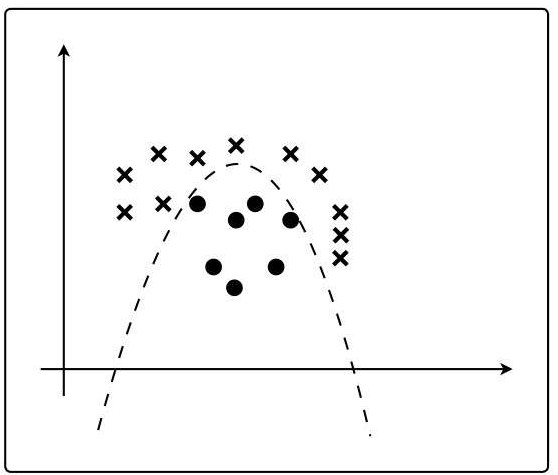
 我们可以像多项式回归一样，增加函数的次数：

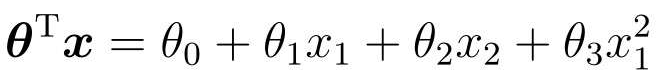
 假设参数，代入试试：

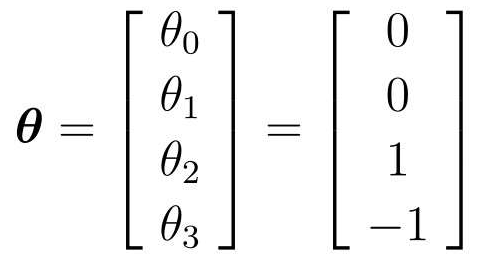
 在图中的表示：

之前的决策边界是直线，现在则是曲线了。参数θ是随便定的，所以数据完全没有被正确地分类。

之后通过随意地增加次数，就可以得到复杂形状的决策边界了。比如在x1*2之外再增加一个x2*2，就会有圆形的决策边界。