文章目录

1、TopK问题

主要思路

程序代码

优越性

2.堆排序

主要思路

程序代码

时间复杂度

---

        堆这个结构实际上还是很有用的，比如TopK问题。

        现在有N个数，要求找最大的前K个。很多人会觉得，这不是很容易吗，排序然后取前K个即可。但是，此时假设N很大，K很小，比如N=100亿，K=10。那么，在这100亿个数字里面，找到最大的前10个，要如何找呢？

        最最重要的是：100亿个数据，实在是太大了，1G 约等于 10亿字节，100亿个数字，就是400亿个字节，则100亿数据约占40G空间。那么，40G在内存中完全开不出来，也就不可能对这么多数据排序。在这里，要用到堆的思想。

1、TopK问题

主要思路

       首先，建立一个有10个数据的小堆（为什么是小堆？）。然后依次遍历数据，只要比堆顶数据大，那么该数据就替换堆顶数据，然后向下调整，重复此过程直到数据遍历结束。最后得到的这个小堆就是100亿个数据里面最大的前10个。

        为什么要建一个小堆呢？而不是大堆？首先要明白，一个堆最能明确的是什么。小堆的堆顶元素，一定是这个堆里面最小的；大堆的堆顶元素，一定是这个堆里面最大的。由于是要寻找最大的前K个数字，那么，建立一个小堆，只要遍历到的数据 A 比堆顶数据 B 大，那么 A 就有资格成为TopK之一，而 B 只能被踢出TopK，相当于用 A 替换 B。

        至于数据 A 是TopK里面最大的还是最小的或者中间的，都不知道，所以要向下调整：数据A 在堆顶，其左右子树没变过，都是小堆，所以向下调整之后，堆里面的最小数据到了堆顶。一直遍历，重复此过程直到结束。

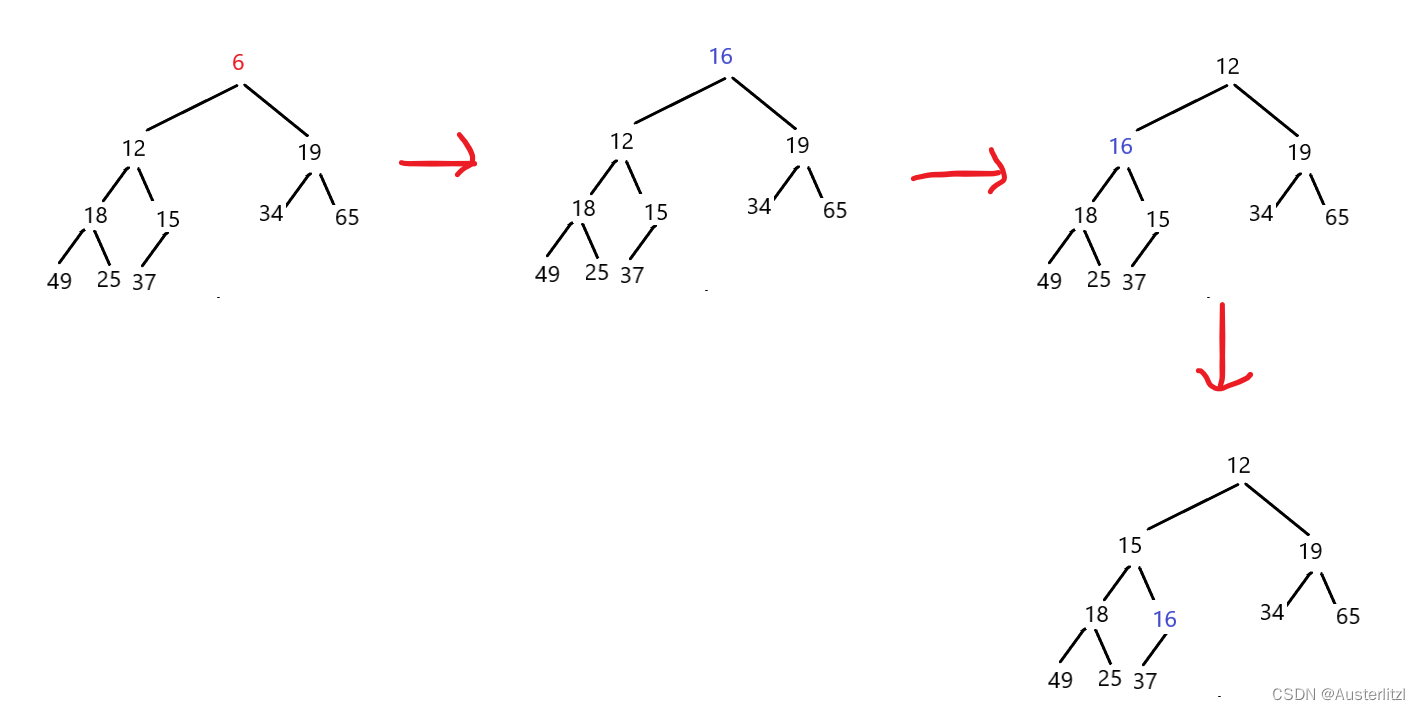
        如下，当前小堆的堆顶数据是6，然后遍历到的数据是16，所以16直接替换堆顶数据，然后向下调整，替换之后的小堆里面 最小的数据到了堆顶 ，而新进的数据 16 也到了该在的位置上。并且，向下调整是十分优越的：在K=10的情况下，每一次向下调整算法，最多只需要移动三次数据。

        当那些数据遍历完之后，在内存中建立的这个小堆，自然就是那100亿个数据里面最大的十个。且不一定是有序的，但是唯一能确定的就是：堆顶数据是最大的十个数据里面，最小的那一个。

程序代码

TopK()
{
	FILE* fout = fopen("test.txt", "w");
	if (fout == NULL)
	{
		perror("fopen fail::");
		return;
	}

	int arr[5] = { 0 };  // k个数据的小堆
	for (int i = 0;i < 5;i++)
	{
		fscanf(fout, "%d", &arr[i]);
		AdjustDown(arr, i);
	}

	int val = 0;
	while (fscanf(fout, "%d", &val) != NULL)//一个一个读取，大于堆顶元素，那么把堆顶变成那个数字，并且向下调整
	{
		if (val > arr[0])
		{
			arr[0] = val;
			AdjustDown(arr, 5);
		}
	}
}

优越性

        其优越性具体体现在时间复杂度上面。如下所示，假设也是寻找最大的前K个数字，除去最开始建堆的K个元素，一共要遍历 N-K 次，不同算法在最坏情况下，每次遍历调整的次数不一样，用堆来做是最好的。

2.堆排序

主要思路

        一个堆，只能明确其堆顶元素是最大还是最小，下面的孩子节点数据，根据其实际存储结构来看，未必是有序的。比如下图，是一个小堆，在实际存储结构上，也只能保证其首元素是最小的，后面的那些元素并不是有序的。所以，堆排序就是要把实际存储结构变成有序。

        那么，以小堆为例，一个小堆，能确定堆顶是最小的，那么可不可以这样想：建堆之后，把堆顶元素单独取出来，就得到了最小的，存到另外一个数组里，再在剩下的数据里面找最小的，循环此过程，新开的数组里就是升序。可是此时又遇到一个问题了：如下，把堆顶元素取出来之后，剩下的就不是一个堆，那么就需要重新建堆。如果数据量小，其实还好，但是数据多了之后，一直建堆就很麻烦。有没有一种方法可以避免这样呢？

         此时，我们可以参考堆操作里面的删除堆顶元素：把堆尾元素拷贝到堆顶，然后去除堆尾元素，进行向下调整，就能把当前堆的最小数据找出来。如下，先把37拷贝到堆顶，然后去掉堆尾的37，再以此从堆顶进行向下调整。

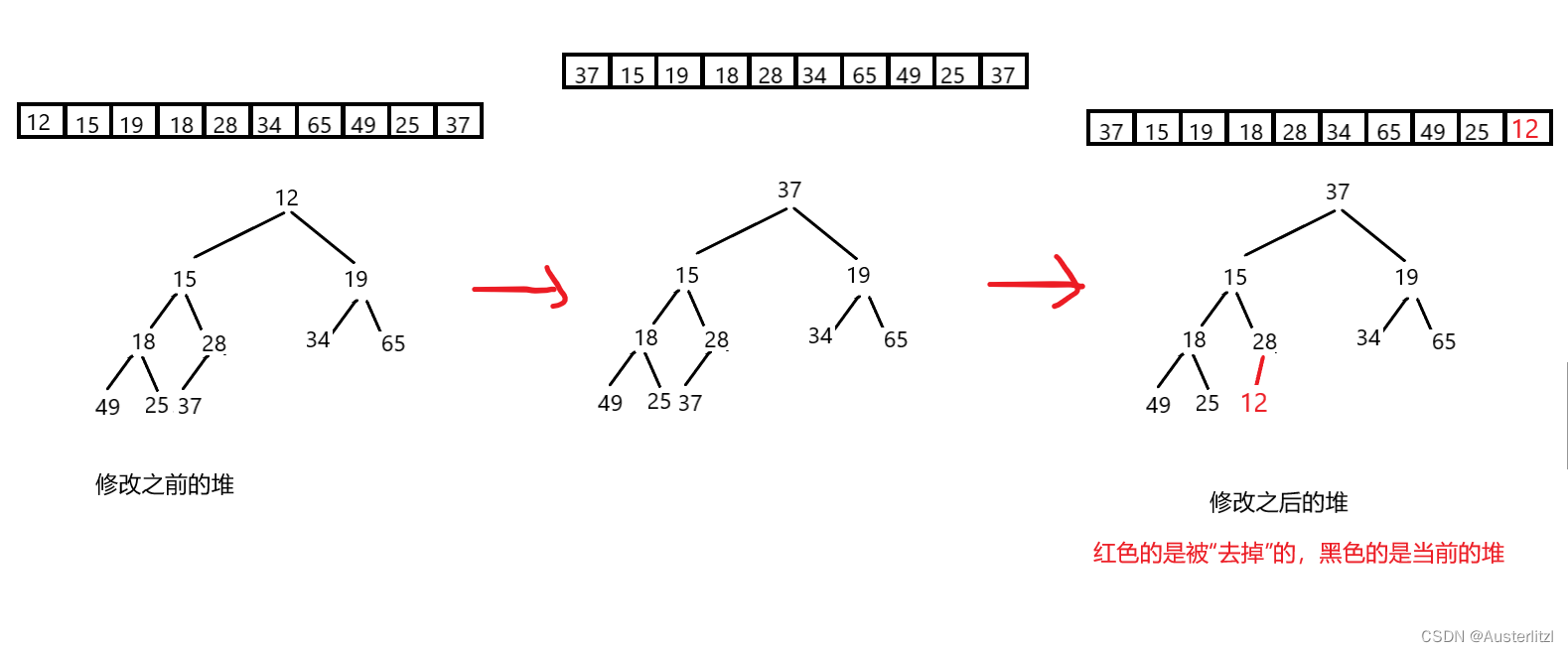
       去掉堆尾 在其物理结构上就相当于 size-- ，实际上那块空间还在，数据也还在，只不过由于size的原因，取不到那里。那么这时我们思考一下，能不能“废物利用”一下下？把“去掉”的那块空间利用起来，存储什么数据？  之前提到，我们要把修改前的堆顶元素放到一个新数组，那么，我们可不可以把堆顶元素放到去掉的那块空间里呢？

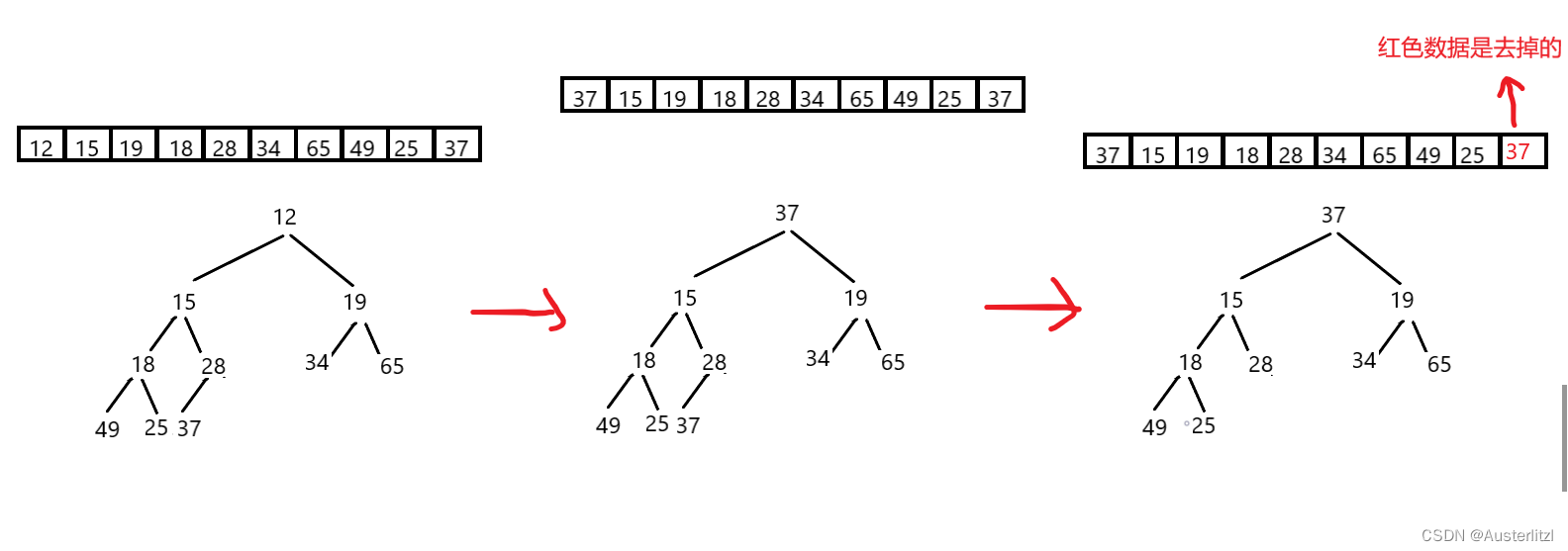
        如下，把修改之前的堆顶元素，放到了被“去掉”的那块空间。下面最右边的那个堆，黑色的才是当前堆，红色是去掉的（画出来只是便于理解）。然后对当前堆（黑色的）进行向下调整，堆顶元素就是当前堆最小的，然后把堆顶元素和当前堆尾元素交换（黑色的）。

        不难想象，一直重复上述操作，最后得到的实际存储结构，从尾到头是从小到大的顺序。那么反过来，正向就是从大到小的顺序，降序。

        当然，如果想要得到升序序列，反着看：在存储结构中，越靠后的数据必然是越大的，所以，要建大堆，大堆的堆顶数据是当前堆里面最大的，堆顶数据从存储结构的末尾依次往前放置，这样子最后得到的就是升序序列。 

程序代码

void Swap(HeapDataType* a, HeapDataType* b)
{
	int c = *a;
	*a = *b;
	*b = c;
}

void HeapSort(HeapDataType* a, int n)
{
	
	//向上调整,时间复杂度是 O（N*log(N)）
	// 每层节点少，调整次数少，节点多，调整次数多，且除了根节点，都要调整。
	//for (int i = 1;i < n;i++)
	//{
	//	AdjustUp(a, i);
	//}

	//向下调整, 时间复杂度是 O(N)
	// 每层节点数量多，调整次数少，节点数量少，调整次数多。且跳过最后一层，接近一半的节点不要调整。
	for (int i = (n - 1 - 1) / 2;i >= 0;i--)
	{
		AdjustDown(a, n, i);
	}
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}

}

时间复杂度

       如下：