【LeetCode热题100】打卡第36天：多数元素&打家劫舍

⛅前言

大家好，我是知识汲取者，欢迎来到我的LeetCode热题100刷题专栏！

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。在此专栏中，我们将会涵盖各种类型的算法题目，包括但不限于数组、链表、树、字典树、图、排序、搜索、动态规划等等，并会提供详细的解题思路以及Java代码实现。如果你也想刷题，不断提升自己，就请加入我们吧！QQ群号：827302436。我们共同监督打卡，一起学习，一起进步。

博客主页💖：知识汲取者的博客

LeetCode热题100专栏🚀：LeetCode热题100

Gitee地址📁：知识汲取者 (aghp) - Gitee.com

题目来源📢：LeetCode 热题 100 - 学习计划 - 力扣（LeetCode）全球极客挚爱的技术成长平台

PS：作者水平有限，如有错误或描述不当的地方，恳请及时告诉作者，作者将不胜感激

多数元素

🔒题目

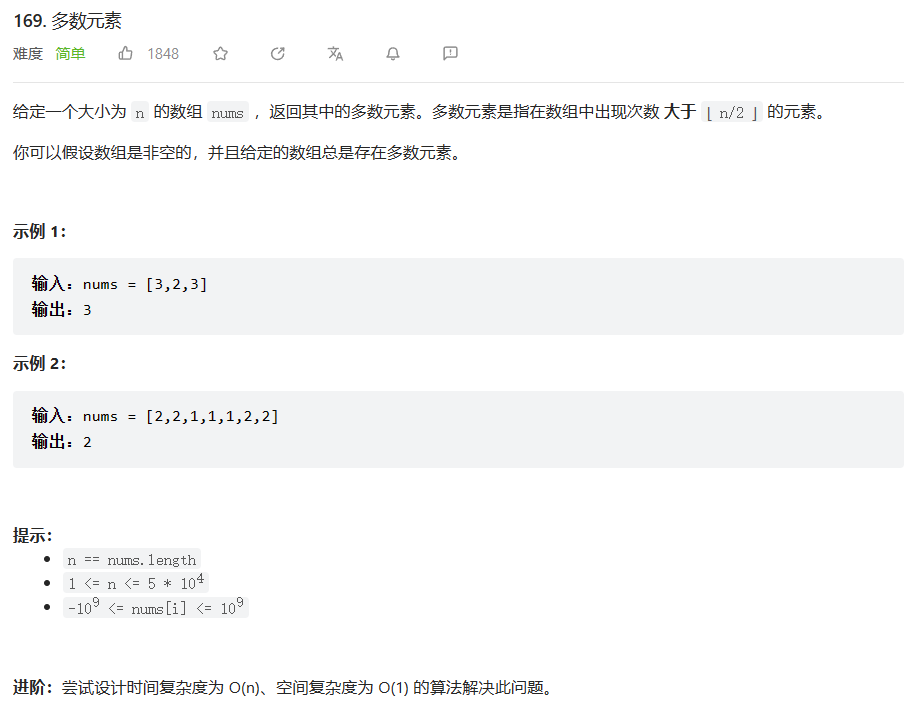
原题链接：169.多数元素

🔑题解

• 解法一：哈希表

  这个思路很简单，使用一个哈希表来映射数组元素与数组元素出现的次数即可

  class Solution {
      public int majorityElement(int[] nums) {
          int target = nums.length / 2;
          Map<Integer, Integer> map = new HashMap<>(16);
          for (int i = 0; i < nums.length; i++) {
              map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);
              Integer value = map.get(nums[i]);
              if (value > target) {
                  return nums[i];
              }
          }
          // 根据题意，这里必不可达，所以这里返回啥都无所谓
          return -1;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(n)$

  其中 $n$ 为数组中元素的个数

• 解法二：排序

  这个相比较哈希表，就更加简单粗暴了🤣我感觉简单题写的采用意思，可以一题多解，拓展思路，对于中等以上的题，很多都只有那一种方式才显得更加优雅（可能是我题写的少吧）

  class Solution {
      public int majorityElement(int[] nums) {
          Arrays.sort(nums);
          return nums[nums.length / 2];
      }
  }
  

  复杂度分析：

  • 时间复杂度：最好$O(nlogn)$，最坏$O(n^2)$，Arrays.sort底层是快排
  • 空间复杂度：$O(logn)$，快排需要logn的栈空间

  其中 $n$ 为数组中元素的个数

• 解法三：Boyer-Moore投票算法（摩尔投票算法）

  这个算法可以说是所有求众数问题的究极解法了🤣，这个算法的诞生就是为了求众数，大家可以自行百度了解一下Boyer-Moore投票算法的诞生。算法的思想也很简单，这里我就详解讲解一下(●’◡’●)

  我们数分为两类，一类是众数，一类不是众数，遇到众数+1，遇到非众数-1。在+1和-1的过程中，可能会出现如下几种情况：

  情况一：count由负数 ==> 0；情况二：count由0 ==> 负数；情况三：count由正数 ==> 0；情况四：count由0 ==> 正数

  由于这群数中，众数的个数>=n/2，所以在遍历的过程中count一定会存在一种状态也就是 0，为什么呢？因为在+1和-1的消耗中，count最开始是0，最终count一定会是一个>=1的值。

  count状态为0可以有两种由来，一种是从正数过来，一种是从负数过来，显然从负数过来的才是众数，最后状态0，也一定是从负数过来的，为什么呢？因为众数的数量要多，count最后一定是正数

  以下是算法的三个示例，大家可以对比着代码看一下

  PS：你可能会感到疑惑，为什么count没有负数❓我们可以把它看成相反数，因为遇到不同的count会-1

  nums    1 1 1 2 2
  mode  0 1 1 1 1 1
  count 0 1 2 3 2 1   
  

  nums    2 2 1 1 1
  mode  0 2 2 2 2 1
  count 0 1 2 1 0 1   
  

  nums    2 1 2 1 1
  mode  0 2 2 2 2 1
  count 0 1 0 1 0 1  
  

  class Solution {
      public int majorityElement(int[] nums) {
          int count = 0;
          int mode = 0;
          for (int num : nums) {
              if (count == 0) {
                  // 状态为0
                  mode = num;
              }
              count += (num == mode) ? 1 : -1;
          }
          return mode;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(1)$

  其中 $n$ 为数组中元素的个数

  趁热打铁：使用摩尔投票算法做完这题，可以接着写这题 【229.多数元素 II】

  略……这里直接给出一种万能解法
  

  /**
   * @author ghp
   * @title 摩尔投票算法万能解法（GPT写的，仅供参考）
   * @description 求解n个数中，次数大于 n/k 的数
   */
  public class Solution {
      private int k = 3;
      public List<Integer> majorityElement(int[] nums) {
          List<Integer[]> majority = new ArrayList<>();
          for (int i = 0; i < k - 1; i++) {
              majority.add(new Integer[]{0, 0});
          }
          for (int num : nums) {
              boolean exist = false;
              Integer idx = null;
              for (int i = 0; i < k - 1; i++) {
                  if (majority.get(i)[0] == 0 && idx == null) {
                      idx = i;
                  }
                  if (majority.get(i)[1] != null && num == majority.get(i)[1]) {
                      majority.get(i)[0] += 1;
                      exist = true;
                      break;
                  }
              }
              if (!exist) {
                  if (idx != null) {
                      majority.get(idx)[0] += 1;
                      majority.get(idx)[1] = num;
                  } else {
                      for (int i = 0; i < k - 1; i++) {
                          majority.get(i)[0] -= 1;
                      }
                  }
              }
          }
          Map<Integer, Integer> checks = new HashMap<>();
          for (Integer[] items : majority) {
              if (items[0] != 0) {
                  checks.put(items[1], 0);
              }
          }
  
          for (int num : nums) {
              if (checks.containsKey(num)) {
                  checks.put(num, checks.get(num) + 1);
              }
          }
          List<Integer> result = new ArrayList<>();
          int s = nums.length / k;
          for (Map.Entry<Integer, Integer> entry : checks.entrySet()) {
              if (entry.getValue() > s) {
                  result.add(entry.getKey());
              }
          }
          return result;
      }
  }
  

打家劫舍

🔒题目

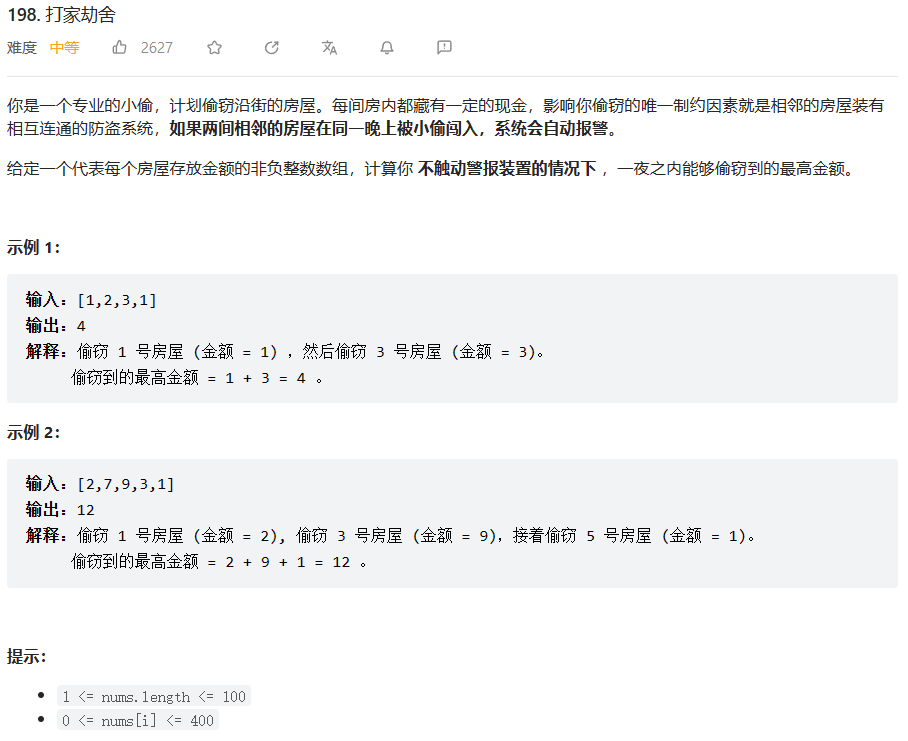
原题链接：198.打家劫舍

🔑题解

• 解法一：暴力枚举+动态规划（能过，但是提交排名超级低，只有5%）

  暴力枚举实现起来也没有想象中的那么简单，我们需要枚举每一种组合，并且做到全局更新最大可偷金额，这里面运用了一点动态规划的思想在里面，当前房子可偷最大金额，①可以是从上一间房子推导而来，②也可以是从上两间房子+当前房子推导而来，也就是cur = Math.max(pre1, pre2 + nums[j])，因为我们不能连续偷，只能至少间隔一间房子偷。

  这里是pre1是存储着上一间房子的最大可偷金额，pre2记录着前两件房子的最大可偷金额，cur代表当前房子最大可偷金额，通过不断更新，最终通过ans = Math.max(ans, cur)更新就可以得到所有房子可偷金额的最大值

  /**
   * @author ghp
   * @title
   * @description
   */
  class Solution {
      public int rob(int[] nums) {
          int ans = 0;
          // 遍历所有可能出现的起始位置
          for (int i = 0; i < nums.length; i++) {
              int cur = 0;
              int pre1 = 0;
              int pre2 = 0;
              // 从当前起始位置开始偷
              for (int j = i; j < nums.length; j++) {
                  cur = Math.max(pre1, pre2 + nums[j]);
                  pre2 = pre1;
                  pre1 = cur;
              }
              ans = Math.max(ans, cur);
          }
          return ans;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n^2)$
  • 空间复杂度：$O(1)$

  其中 $n$ 为数组中元素的个数

• 解法二：动态规划

  其实，从上面的题解中，我们就已经大致可以摸清那个状态转移的规律了。前面的题解中，每次我们都要从重新计算 i 到 nums.length 之间的最大值，然后计算 i+1 到 nums.length 之间的最大值，很明显 i 是包括了 i+1 的，所以我们可以使用一个dp数组来记录每一个房间可偷的最大值，则当前房间可偷最大值①可以是从上一间房子推导而来，②也可以是从上两间房子+当前房子推导而来，也就有了dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i])，唯一需要注意的就是初始化时要防止NPE，这题应该也算是一个入门级别的 动态规划题了

  class Solution {
      public int rob(int[] nums) {
          if (nums.length == 1){
              return nums[0];
          }
          int n = nums.length;
          int[] dp = new int[n];
          dp[0] = nums[0];
          dp[1] = Math.max(nums[0], nums[1]);
          for (int i = 2; i < n; i++) {
              // 更新当前房间可偷最大值
              dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
          }
          return dp[n - 1];
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(n)$

  其中 $n$ 为数组中元素的个数

  代码优化：空间优化

  解法一中，我们通过使用一个pre1和pre2来记录上一间房子可偷最大金额和前两间房子能偷的最大金额，我们可以直到当前房子的状态至于前两个防止的状态有关，所以我们完全可以使用两个变量来记录这两个状态，而不是使用dp数组

  pre1：前一间（也就是第i-1间）房子可偷最大金额；pre2：前两间房子（也就是第i-2间）房子可偷最大金额；cur：当前（第i间）房子可偷最大金额

  class Solution {
      public int rob(int[] nums) {
          if (nums.length == 1) {
              return nums[0];
          }
          int pre1 = Math.max(nums[0], nums[1]);
          int pre2 = nums[0];
          int cur = Math.max(pre1, pre2);
          for (int i = 2; i < nums.length; i++) {
              cur = Math.max(pre1, pre2 + nums[i]);
              pre2 = pre1;
              pre1 = cur;
          }
          return cur;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(1)$

  其中 $n$ 为数组中元素的个数