数据结构初阶--顺序表

news2024/9/24 1:24:09

目录

一.顺序表的定义

二.顺序表的分类

2.1.静态顺序表

2.2.动态顺序表

三.顺序表的特点

四.顺序表的功能实现

4.1.顺序表的定义

4.2.顺序表的初始化

4.3.顺序表的销毁

4.4.顺序表的容量检查

4.5.顺序表的打印

4.6.顺序表的尾插

4.7.顺序表的头插

4.8.顺序表的尾删

4.9.顺序表的头删

4.10.顺序表的任意位置插入

4.11.顺序表的任意位置删除

4.12.顺序表的查找某个元素

4.13.顺序表的某个位置上的值的修改

4.14.完整程序

SeqList.h

SeqList.c

test.c

五.顺序表刷题

题一：移除元素

题二：去重算法

题三：合并两个有序数组

一.顺序表的定义

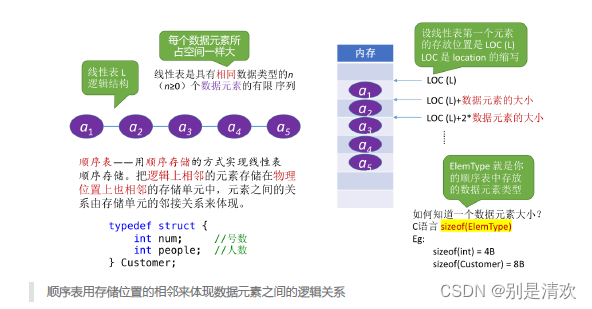
线性表：是具有相同数据类型的n(n>=0)个数据元素的有限序列。

顺序表：用顺序存储的方式实现线性表。

顺序存储：把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中，元素之间的关系由存储单元的邻接关系来体现。

二.顺序表的分类

2.1.静态顺序表

#define MaxSize 100 //定义最大长度
typedef int ElemType;

typedef struct
{
	ElemType data[MaxSize];//用静态的数组存放数据元素
	int length;//顺序表的当前长度
}SeqList;//顺序表的类型定义

//初始化一个顺序表
void InitList(SeqList* L)
{
	L->length = 0;//顺序表初始长度为0
}

声明一个顺序表时在内存中分配存储顺序表L的连续空间。包括：MaxSize*sizeof(ElemType)和存储Length的空间。                                                                                                                                         初始化顺序表时可以不用把各个数据元素的值设为默认值，直接将Length的值设为0即可。尽管内存中会有遗留的“脏数据”，但是因为访问超过当前长度的值是违法的，所以并不会有什么影响。尽量使用基本操作来访问顺序表中的各个数据元素。

2.2.动态顺序表

因为静态顺序表的表长开始确定后就无法更改(存储空间是静态的)，刚开始就声明一个很大的内存空间又很浪费。所以可以用动态分配的方式实现顺序表大小可变。

#define InitSize 100  //顺序表的初始长度
typedef int ElemType;

typedef struct
{
	ElemType* data;//指示动态分配数组的指针
	int MaxSize;//顺序表的最大容量
	int length;//顺序表的当前长度
}SeqList;//顺序表的类型定义

//初始化一个顺序表
void InitList(SeqList* L)
{
	L->length = 0;//顺序表初始长度为0
	L->MaxSize = InitSize;
}

C提供了malloc和free函数来实现动态申请和释放内存空间。使用时加头文件#include<stdlib.h>。malloc函数会申请一整片连续的存储空间，返回指向这片存储空间开始地址的指针。需要强制转型来决定这片存储空间用来存储什么类型的数据元素。如

L.data=(ElemType*)malloc(sizeof(ElemType)*InitSize);

就强制转型为了你定义的数据元素类型指针，并让data指针变量指向这一整片存储空间的起始地址，也就是顺序表的第一个数据元素。

三.顺序表的特点

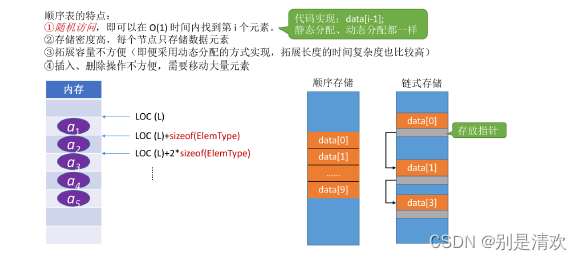
四.顺序表的功能实现

4.1.顺序表的定义

typedef int SLDataType;

//静态顺序表：N太小，可能不够用；N太大，可能浪费空间
//动态顺序表：大小可以自动调节
typedef struct SeqList
{
	SLDataType* a;//动态数组
	int size;//当前元素个数
	int capacity;//空间大小
}SL;

4.2.顺序表的初始化

void SLInit(SL* ps)
{
	assert(ps);
	//assert(ps!=NULL);

	ps->a = NULL;
	ps->size = ps->capacity = 0;
}

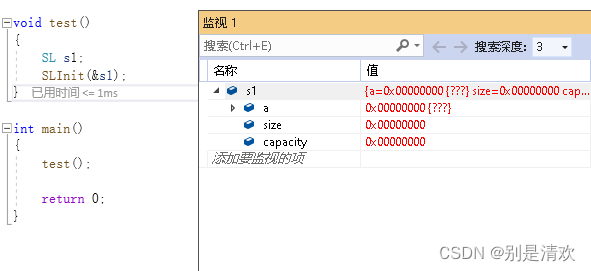
需要注意的是：实参传给形参，是将实参的值拷贝给形参，对形参的值进行修改并不会影响实参，因为它是值传递，所以需要改成传地址。

调试分析：

4.3.顺序表的销毁

void SLDestory(SL* ps)
{
	assert(ps);

	if (ps->a)
	{
		free(ps->a);
		ps->a = NULL;

		ps->capacity = ps->size = 0;
	}
}

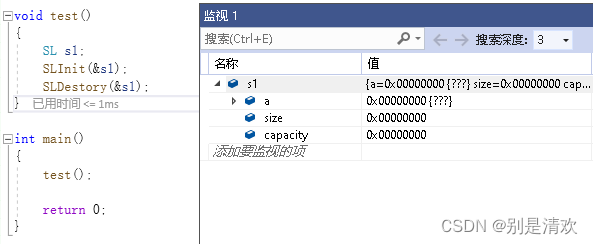
在进行动态内存分配时，需要调用malloc，realloc等函数进行内存空间的开辟。在使用完毕之后，要对所开辟的内存空间进行回收，这时就要调用free函数进行内存空间的释放。

调试分析：

4.4.顺序表的容量检查

void SLCheckCapacity(SL* ps)
{
	assert(ps);

	//检查容量空间，若容量为空，则将元素个数设置为4；若容量满了，则将空间容量设置为起始容量的二倍
	if (ps->size == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;//若capacity的初始值为0，则扩容4个元素，否则，容量扩大两倍

		SLDataType* tmp = (SLDataType*)realloc(ps->a, newCapacity * sizeof(SLDataType));//原地扩容，异地扩容

		if (tmp == NULL)
		{
			perror("realloc");
			//return;
			exit(-1);
		}

		ps->a = tmp;
		ps->capacity = newCapacity;
	}
}

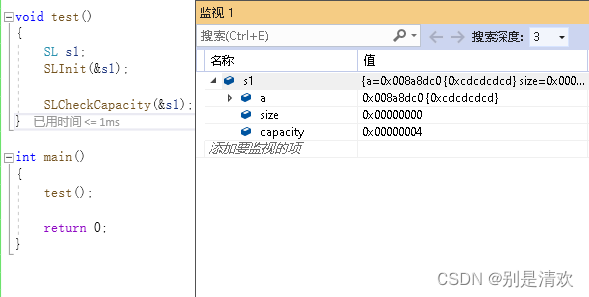
当ps->size < ps->capacity时，此时进行元素的插入显然是不需要对容量进行检查的。只有当ps->size == ps->capacity时，此时进行元素的插入才会对容量进行检查。                                      当ps->size == ps->capacity == 0时，若要插入元素，此时容量为空，无法插入新的元素，通过调用realloc函数开辟4个元素的内存空间。当ps->size == ps->capacity != 0时，若要插入元素，此时容量已满，无法插入新的元素，通过调用realloc函数开辟2*ps->capacity个元素的内存空间。

调试分析：

4.5.顺序表的打印

void SLPrint(SL* ps)
{
	assert(ps);

	for (int i = 0; i < ps->size; ++i)
	{
		printf("%d ",ps->a[i]);
	}

	printf("\n");
}

即将顺序表的元素依次输出。

4.6.顺序表的尾插

void SLPushBack(SL* ps, SLDataType x)
{
	assert(ps);

	//检查容量
	SLCheckCapacity(&ps);

	ps->a[ps->size] = x;
	ps->size++;
}

在插入元素之前，首先要做的就是对空间容量的检查。若空间已满，则进行扩容再在末尾插入新的元素；若空间未满，则直接在末尾插入新的元素。                                                                                    先在数组下标为size的位置插入新的元素x，再将ps->size++。

调试分析：

运行结果：

4.7.顺序表的头插

void SLPushFront(SL* ps, SLDataType x)
{
	assert(ps);

	//检查容量
	SLCheckCapacity(ps);

	//从后往前移
	int end = ps->size - 1;
	while (end >= 0)
	{
		ps->a[end + 1] = ps->a[end];
		--end;
	}
	
	//放入数据
	ps->a[0] = x;
	ps->size++;
}

同尾插一样，在插入元素之前需要对空间容量进行判断。若空间充足，则要把第0个位置开始的ps->size个元素全部后移一位，再在第0个位置上填入要插入的元素x；若空间不足，则先扩容再在数组头部插入元素x。

调试分析：

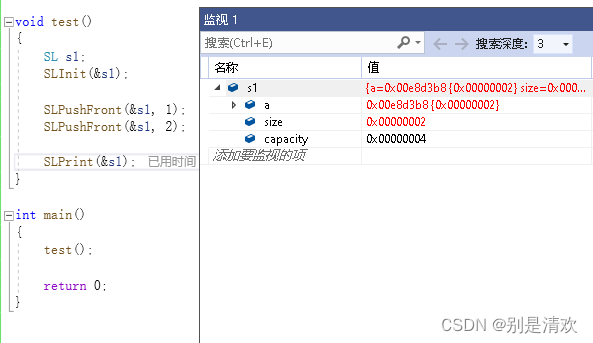
运行结果：

4.8.顺序表的尾删

void SLPopBack(SL* ps)
{
	assert(ps);

	//温柔检查
	//if (ps->size == 0)
	//{
	//	printf("SeqList is empty\n");
	//	return;
	//}
	
	//暴力检查
	assert(ps->size > 0);

	ps->size--;
}

在对数组进行尾删时，可能会存在越界问题。当不使用assert(ps->size > 0)时，越界并不报错，只有在销毁SLDestory(&s1)之后，才会对越界问题进行检查与报错。需要注意的是：越界是不一定报错的，系统对越界的检查，是设岗抽查。

案例分析：

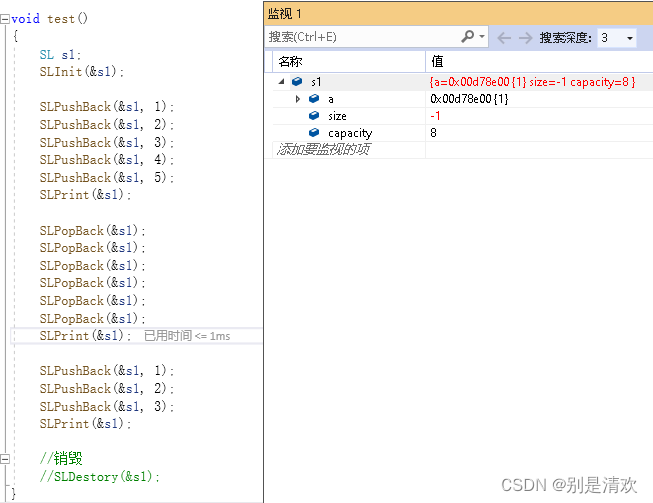
在尾插了5个元素之后，又进行了6次尾删，此时的ps->size=-1，显然已经越界，但是系统并没有报错。 所以针对潜在的越界问题，需要进行特殊处理。通常采用的方法是：在执行ps->size--时，先进行assert(ps->size > 0)判断。

在加上assert(ps->size > 0)判断之后，再执行程序得：

4.9.顺序表的头删

void SLPopFront(SL* ps)
{
	assert(ps);

	assert(ps->size > 0);

	//从前往后移动数据
	int begin = 1;
	while (begin < ps->size)
	{
		ps->a[begin - 1] = ps->a[begin];
		++begin;
	}

	ps->size--;
}

头删与尾删相类似，都存在数组越界问题，在删除之前都需要进行assert(ps->size > 0)的判断，案例与尾删相同，这里就不再进行举例分析。

调试分析：

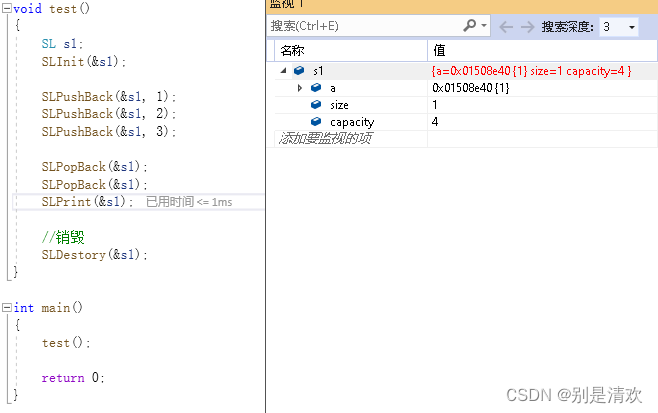
运行结果：

4.10.顺序表的任意位置插入

void SLInsert(SL* ps, int pos, SLDataType x)
{
	assert(ps!=NULL);
	assert(pos >= 0 && pos <= ps->size);

	//检查容量
	SLCheckCapacity(ps);

	//从后往前移动数据
	int end = ps->size - 1;

	while (end >= pos)
	{
		ps->a[end + 1] = ps->a[end];
		--end;
	}

	ps->a[pos] = x;
	ps->size++;
}

在插入数据之前，要进行插入位置pos合法性的判断。首先pos >= 0，因为数组的下标是从0开始的。其次pos <= ps->size，因为数组的最大下标为ps->size-1，而插入的位置可以在最后一个元素的后面。插入的位置一定要保证数组的连贯性，中间不能存在空缺。因此，为了避免下标越界，在插入数据之前，需要进行assert(pos >= 0 && pos <= ps->size)的判断。

同时，在插入元素时，一定要判断空间容量的大小，若不足则直接调SLCheckCapacity(ps)进行扩容。

调试分析：

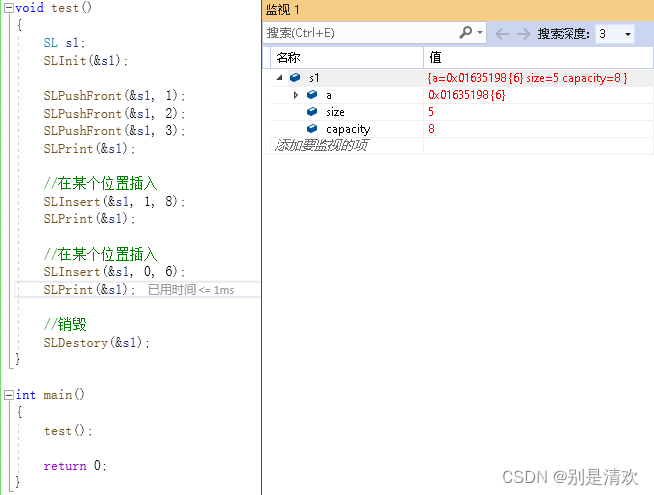
运行结果：

拓展：

既然函数void SLInsert(SL* ps, int pos, SLDataType x)是在任意位置进行插入，那么我们可以将顺序表的头插函数void SLPushFront(SL* ps, SLDataType x)与尾插函数void SLPushBack(SL* ps, SLDataType x)进行改写：

顺序表的头插：

void SLPushFront(SL* ps, SLDataType x)
{
	SLInsert(ps, 0, x);
}

顺序表的尾插：

void SLPushBack(SL* ps, SLDataType x)
{
	SLInsert(ps, ps->size, x);
}

4.11.顺序表的任意位置删除

void SLErase(SL* ps, int pos)
{
	assert(ps);
	assert(pos >= 0 && pos < ps->size);//不能等于size

	/*
	//注意越界问题
	//法1：
	int begin = pos;
	while (begin < ps->size-1)
	{
		ps->a[begin] = ps->a[begin+1];
		++begin;
	}
	*/

	//法2
	int begin = pos + 1;
	while (begin < ps->size)
	{
		ps->a[begin - 1] = ps->a[begin];
		++begin;
	}

	ps->size--;
}

在删除数据之前，要进行删除位置pos合法性的判断。首先pos >= 0，因为数组的下标是从0开始的。其次pos < ps->size，因为数组的最大下标为ps->size-1。因此，为了避免下标越界，在删除数据之前，需要进行assert(pos >= 0 && pos < ps->size)的判断。

调试分析：

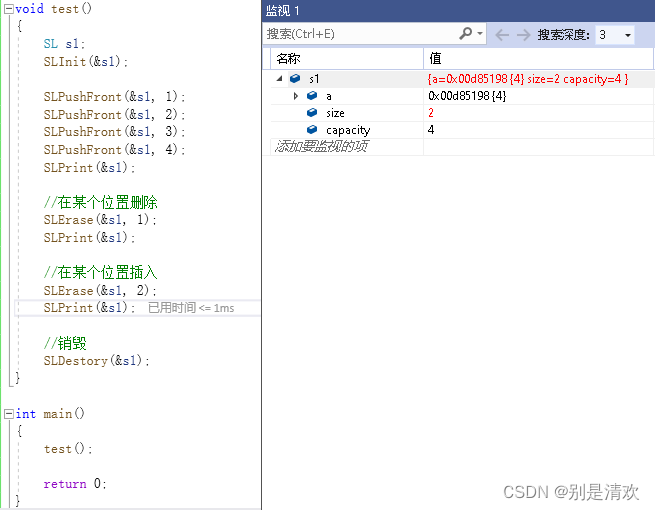
运行结果：

4.12.顺序表的查找某个元素

int SLFind(SL* ps, SLDataType x)
{
	assert(ps);

	for (int i = 0; i < ps->size; ++i)
	{
		if (ps->a[i] == x)
		{
			return i;
		}
	}

	return -1;
}

案例： 

void test()
{
	SL s1;
	SLInit(&s1);

	SLPushFront(&s1, 1);
	SLPushFront(&s1, 2);
	SLPushFront(&s1, 3);
	SLPushFront(&s1, 4);
	SLPushFront(&s1, 5);
	SLPrint(&s1);

	int x = 0;
	printf("请输入你要查找的值：");
	scanf("%d", &x);
	int pos = SLFind(&s1, x);
	//返回对应元素的下标
	printf("查找元素的下标为：%d\n",pos);

	//销毁
	SLDestory(&s1);
}

int main()
{
	test();

	return 0;
}

运行结果：

扩展：

如何查找顺序表中某个元素，并删除所有相同的元素？

与函数int SLFind(SL* ps, SLDataType x)不同的是，函数int SLFindPlus(SL* ps, SLDataType x, int begin)多了一个起始的begin值以及修改了这个循环的起始条件。

案例：

int SLFindPlus(SL* ps, SLDataType x, int begin)
{
	assert(ps);
	for (int i = begin; i < ps->size; ++i)
	{
		if (ps->a[i] == x)
		{
			return i;
		}
	}
	return -1;
}

void Test()
{
	SL s1;
	SLInit(&s1);

	SLPushFront(&s1, 1);
	SLPushFront(&s1, 2);
	SLPushFront(&s1, 3);
	SLPushFront(&s1, 4);
	SLPushFront(&s1, 3);
	SLPrint(&s1);

	int x = 0;
	printf("请输入你要删除的值：");
	scanf("%d", &x);
	//查找某个值
	int pos = SLFind(&s1, 3, 0);

	while (pos != -1)
	{
		SLErase(&s1, pos);
		pos = SLFind(&s1, 3, pos);//更新下一个位置
	}

	SLPrint(&s1);
}

int main()
{
	Test();

	return 0;
}

运行结果：

4.13.顺序表的某个位置上的值的修改

void SLModify(SL* ps, int pos, SLDataType x)
{
	assert(ps);
	assert(pos >= 0 && pos < ps->size);

	ps->a[pos] = x;
}

案例：

void test()
{
	SL s1;
	SLInit(&s1);

	SLPushFront(&s1, 1);
	SLPushFront(&s1, 2);
	SLPushFront(&s1, 3);
	SLPushFront(&s1, 4);
	SLPushFront(&s1, 5);
	SLPrint(&s1);

	int y, z = 0;
	printf("请输入你要修改的值和修改后的值：");
	scanf("%d %d", &y, &z);
	//查找某个位置
	int pos = SLFind(&s1, y);

	if (pos != -1)
	{
		SLModify(&s1, pos, z);
	}
	else
	{
		printf("没有找到：%d\n", y);
	}

	//打印
	SLPrint(&s1);

	//销毁
	SLDestory(&s1);
}

int main()
{
	test();

	return 0;
}

运行结果：

4.14.完整程序

SeqList.h

#pragma once

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>

typedef int SLDataType;

//静态顺序表：N太小，可能不够用；N太大，可能浪费空间
//动态顺序表：大小可以自动调节
typedef struct SeqList
{
	SLDataType* a;//动态数组
	int size;//当前元素个数
	int capacity;//空间大小
}SL;

//尾插，尾删的时间复杂度为：O(1)
//头插，头删的时间复杂度为：O(N)

//初始化
void SLInit(SL* ps);

//检查容量
void SLCheckCapacity(SL* ps);

//打印
void SLPrint(SL* ps);

//销毁
void SLDestory(SL* ps);

//尾插
void SLPushBack(SL* ps, SLDataType x);

//头插
void SLPushFront(SL* ps, SLDataType x);

//尾删
void SLPopBack(SL* ps);

//头删
void SLPopFront(SL* ps);

//在某个位置插入
void SLInsert(SL* ps, int pos, SLDataType x);

//在某个位置删除
void SLErase(SL* ps, int pos);

//查找某个元素
int SLFind(SL* ps, SLDataType x);

//修改某个位置上的值
void SLModify(SL* ps, int pos, SLDataType x);

SeqList.c

#define _CRT_SECURE_NO_WARNINGS 1

#include"SeqList.h"


//初始化
void SLInit(SL* ps)
{
	assert(ps);
	//assert(ps!=NULL);

	ps->a = NULL;
	ps->size = ps->capacity = 0;
}


//检查容量
void SLCheckCapacity(SL* ps)
{
	assert(ps);

	//检查容量空间，若容量为空，则将元素个数设置为4；若容量满了，则将空间容量设置为起始容量的二倍
	if (ps->size == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;//若capacity的初始值为0，则扩容4个元素，否则，容量扩大两倍

		SLDataType* tmp = (SLDataType*)realloc(ps->a, newCapacity * sizeof(SLDataType));//原地扩容，异地扩容

		if (tmp == NULL)
		{
			perror("realloc");
			//return;
			exit(-1);
		}

		ps->a = tmp;
		ps->capacity = newCapacity;
	}
}


//打印
void SLPrint(SL* ps)
{
	assert(ps);

	for (int i = 0; i < ps->size; ++i)
	{
		printf("%d ",ps->a[i]);
	}

	printf("\n");
}


//销毁
void SLDestory(SL* ps)
{
	assert(ps);

	if (ps->a)
	{
		free(ps->a);
		ps->a = NULL;

		ps->capacity = ps->size = 0;
	}
}


//尾插
void SLPushBack(SL* ps, SLDataType x)
{
	/*
	assert(ps);

	//检查容量
	SLCheckCapacity(&ps);

	ps->a[ps->size] = x;
	ps->size++;
	*/

	SLInsert(ps, ps->size, x);
}


//头插
void SLPushFront(SL* ps, SLDataType x)
{
	/*
	assert(ps);

	//检查容量
	SLCheckCapacity(ps);

	//从后往前移
	int end = ps->size - 1;
	while (end >= 0)
	{
		ps->a[end + 1] = ps->a[end];
		--end;
	}
	
	//放入数据
	ps->a[0] = x;
	ps->size++;
	*/

	SLInsert(ps, 0, x);
}


//尾删
void SLPopBack(SL* ps)
{
	/*
	assert(ps);

	//温柔检查
	//if (ps->size == 0)
	//{
	//	printf("SeqList is empty\n");
	//	return;
	//}
	
	//暴力检查
	//assert(ps->size > 0);

	ps->size--;
	*/
	
	SLErase(ps, ps->size-1);
}


//头删
void SLPopFront(SL* ps)
{
	/*
	assert(ps);

	assert(ps->size > 0);

	//从前往后移动数据
	int begin = 1;
	while (begin < ps->size)
	{
		ps->a[begin - 1] = ps->a[begin];
		++begin;
	}

	ps->size--;
	*/

	SLErase(ps, 0);
}


//在某个位置插入
void SLInsert(SL* ps, int pos, SLDataType x)
{
	assert(ps!=NULL);
	assert(pos >= 0 && pos <= ps->size);

	//检查容量
	SLCheckCapacity(ps);

	//从后往前移动数据
	int end = ps->size - 1;

	while (end >= pos)
	{
		ps->a[end + 1] = ps->a[end];
		--end;
	}

	ps->a[pos] = x;
	ps->size++;
}


//在某个位置删除
void SLErase(SL* ps, int pos)
{
	assert(ps);
	assert(pos >= 0 && pos < ps->size);//不能等于size

	/*
	//注意越界问题
	//法1：
	int begin = pos;
	while (begin < ps->size-1)
	{
		ps->a[begin] = ps->a[begin+1];
		++begin;
	}
	*/

	//法2
	int begin = pos + 1;
	while (begin < ps->size)
	{
		ps->a[begin - 1] = ps->a[begin];
		++begin;
	}

	ps->size--;
}


//查找某个元素
int SLFind(SL* ps, SLDataType x)
{
	assert(ps);

	for (int i = 0; i < ps->size; ++i)
	{
		if (ps->a[i] == x)
		{
			return i;
		}
	}

	return -1;
}

//修改某个位置上的值
void SLModify(SL* ps, int pos, SLDataType x)
{
	assert(ps);
	assert(pos >= 0 && pos < ps->size);

	ps->a[pos] = x;
}

test.c

#define _CRT_SECURE_NO_WARNINGS 1

#include "SeqList.h"

void TestList7()
{
	SL s1;

	//初始化
	SLInit(&s1);//实参传给形参，是将实参的值拷贝给形参，形参值的修改并不会影响实参，它是值传递，需要改成传地址

	//尾插
	SLPushFront(&s1, 1);
	SLPushFront(&s1, 2);
	SLPushFront(&s1, 3);
	SLPushFront(&s1, 4);
	SLPushFront(&s1, 5);

	//打印
	SLPrint(&s1);

	//在某个位置删除
	SLErase(&s1, 3);
	SLErase(&s1, 2);

	//打印
	SLPrint(&s1);

	//头删
	SLPopFront(&s1);

	//尾删
	SLPopBack(&s1);

	//打印
	SLPrint(&s1);

	//销毁
	SLDestory(&s1);
}

int main()
{
	TestList7();

	return 0;
}

五.顺序表刷题

题一：移除元素

题目描述：

给你一个数组nums和一个值val，你需要原地移除所有数值等于val的元素，并返回移除后数组的新长度
不要使用额外的数组空间，你必须仅使用O(1)额外空间并原地修改输入数组
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素
要求时间复杂度：O(N)，空间复杂度：O(1)

分析：

法一：

覆盖删除  时间复杂度：O(N^2)，空间复杂度：O(1)

找到所有的val，每次挪动val后的数据覆盖删除val。重复执行，直到删除所有的val。

实现：

int find(int* nums, int numsSize, int val)
{
	int i = 0;
	for (i = 0; i < numsSize; i++)
	{
		if (nums[i] == val)
			return i;
	}
	return -1;
}

int removeElement(int* nums, int numsSize, int val)
{
	int ret = 0;
	while ((ret = find(nums, numsSize, val)) != -1)
	{
		for (int i = ret; i < numsSize - 1; i++)
		{
			nums[i] = nums[i + 1];
		}
		numsSize--;
	}
	return numsSize;
}

法二：

保留不是val的值，移到新数组  时间复杂度：O(N)，空间复杂度：O(N)

创建一个临时数组tmp，然后遍历nums数组，把不是val的数值全都放到tmp数组，最后把tmp数组的内容依次拷贝到nums数组，并返回tmp数组长度。

int removeElement(int* nums, int numsSize, int val)
{
	if (numsSize == 0)//特殊处理
		return 0;

	int i = 0;
	int tmp[numsSize] = { 0 };

	int count = 0;
	for (i = 0; i < numsSize; i++)
	{
		if (nums[i] != val)
		{
			tmp[count] = nums[i];
			count++;
		}
	}

	for (i = 0; i < numsSize; i++)
	{
		nums[i] = tmp[i];
	}

	return count;
}

法三：

保留不是val的值，覆盖前面的值  时间复杂度：O(N)，空间复杂度：O(1)

创建两个变量src和dst，初始时均指向nums首部。首先判断nums[src]是否等于val，如果等于val，则src向后移动，dst保持则不动。重复上述操作，当nums[src]!=val，令nums[dst]=nums[src]，然后src、dst均向后偏移，直至src遍历完整个nums数组。

实现：

int removeElement(int* nums, int numsSize, int val)
{
	int src = 0;
	int dst = 0;

	while (src < numsSize)
	{
		if (nums[src] != val)
		{
			nums[dst++] = nums[src++];
		}
		else
		{
			src++;
		}
	}

	return dst;
}

题二：去重算法

描述：

删除有序数组中的重复项
给你一个升序排序的数组nums，请你原地删除重复出现的元素，使每个元素只出现一次，返回删除后数组的新长度，元素的相对顺序应该保持一致
不要使用额外的空间，你必须在原地修改输入数组并在使用O(1)额外空间的条件下完成

法一：

创建两个变量src和dst，初始时src=1,dst=0。首先判断nums[src]是否等于nums[dst]，如果相等，则src向后移动，dst保持则不动；若不相等，则dst向后移动，同时将nums[src]的值赋给nums[dst]，赋值成功之后，再将src向后移动一位。重复上述操作，直至scr遍历完整个数组。

实现：

int removeDuplicates(int* nums, int numsSize)
{
	int src = 1;
	int dst = 0;
	while (src < numsSize)
	{
		if (nums[src] == nums[dst])
		{
			src++;
		}
		else
		{
			dst++;
			nums[dst] = nums[src];
			src++;
		}
	}

	return dst + 1;
}

法二：

覆盖删除  时间复杂度：O(N)，空间复杂度：O(1)
遍历整个数组，比较相邻两个元素是否相等，如果相等就把后一个相等元素后面的所有元素都往前移动，同时numsSize–。

int removeDuplicates(int* nums, int numsSize)
{
	for (int i = 0; i < numsSize - 1; i++) 
	{
		//如果相邻的元素相等，那么就用后面的元素覆盖前面的元素
		if (nums[i] == nums[i + 1]) 
		{
			for (int j = i; j < numsSize - 1; j++) 
			{
				nums[j] = nums[j + 1];
			}
			numsSize--; //覆盖结束后，数组元素个数-1 

			i--; //上面的程序执行完毕之后，i会自动i++，而因为后面的元素会覆盖前面的元素，所以下标要更新
		}

	}
	return numsSize;
}

题三：合并两个有序数组

描述：

给你两个按非递减顺序排列的整数数组nums1和nums2，另有两个整数m和n，分别表示nums1和nums2的元素数目
请你合并nums2到nums1中，使合并后的数组同样按非递减顺序排列
注意：最终，合并后的数组不应由函数返回，而是存在存储在数组nums1中。为了应对这种情况，nums1的初始长度为m+n

分析：

法一：开辟一个额外的数组  时间复杂度：O(n+m)，空间复杂度：O(n+m)
法二：从后向前比较，然后逐一拷贝  时间复杂度：O(n+m)，空间复杂度：O(1)
从nums1和nums2的最后一位有效位开始比较，然后由后向前，哪个元素大就放到数组nums1的最后的位置，重复上述操作，直到其中一个数组比较完毕。在比较完后也要进行一次判断：如果nums1已经比较完毕，而nums2还没有，那么直接把nums2剩余的元素都拷贝到nums1即可。

实现：

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n)
{
	int end1 = m - 1;
	int end2 = n - 1;
	int end = m + n - 1;

	while (end1 >= 0 && end2 >= 0)
	{
		if (nums1[end1] > nums2[end2])
		{
			nums1[end--] = nums1[end1--];
		}
		else
		{
			nums1[end--] = nums2[end2--];
		}
	}

	//end1结束则合并结束，若end2未结束，则将end2剩余的元素全部拷贝到end1中
	while (end2 >= 0)
	{
		nums1[end--] = nums2[end2--];
	}
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/749027.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

用ChatGPT搞定12 种编程语言：看看它如何表现

用ChatGPT搞定12 种编程语言：看看它如何表现

众所周知ChatGPT可以写代码&#xff0c;但当有一堆语言一起抛向它时&#xff0c;它的表现如何呢&#xff1f;答案是&#xff1a;还不错&#xff08;但并不完美&#xff09;。 在过去的几个月里&#xff0c;我们已经领教了ChatGPT的编码能力。我对它进行了PHP和WordPress的测试…
阅读更多...
前端学习——Web API (Day6)

前端学习——Web API (Day6)

正则表达式 语法 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"widthdevice…
阅读更多...
SPEC CPU 2017 1.0.5 不同版本CentOS 7 8 安装笔记

SPEC CPU 2017 1.0.5 不同版本CentOS 7 8 安装笔记

CentOS 7.9.2009 x86_64 gcc版本 安装成功 runcpu编译报错 gcc版本太低&#xff0c;不识别-fno-tree-loop-vectorize 去掉config/gcc.cfg中 -fno-tree-loop-vectorize编译优化参数。 用例编译中 CentOS 8.3.2011 x86_64 gcc版本 安装失败&#xff0c;需要自行编译tools 手动…
阅读更多...
#{} 和 ${} 的区别？

#{} 和 ${} 的区别？

一、区别概述 1.1、主要区别&#xff1a; 1、#{} 是预编译处理&#xff0c;${} 是直接替换&#xff1b;2、${} 存在SQL注入的问题&#xff0c;而 #{} 不存在&#xff1b;Ps&#xff1a;这也是面试主要考察的部分~ 1.2、细节上&#xff1a; 1、${} 可以实现排序查询&#xff…
阅读更多...
亚马逊云科技联合Nolibox定制工业设计AIGC解决方案

亚马逊云科技联合Nolibox定制工业设计AIGC解决方案

从机器学习算法到深度学习再到强化学习&#xff0c;AI创新浪潮奔流不息。而AIGC&#xff08;AI-generated Content&#xff0c;人工智能生成内容&#xff09;的到来&#xff0c;更是让AI成为众多企业的得力助手&#xff0c;开拓了文本、图像、音视频等领域的天花板。 在洞悉到…
阅读更多...
企业云性能监控是一项关键的任务

企业云性能监控是一项关键的任务

企业云性能监控是一项关键的任务&#xff0c;它不仅可以保障企业云服务的稳定性和可靠性&#xff0c;还可以加强企业对云服务的掌控和管理&#xff0c;提供卓越的用户体验。 首先&#xff0c;企业云性能监控可以保障云服务的稳定和可靠。在云计算环境下&#xff0c;企业的核心业…
阅读更多...
#1336 .「找树根和孩子」. [树的基本使用]（内附封面）

#1336 .「找树根和孩子」. [树的基本使用]（内附封面）

【题目描述】 给定一棵树&#xff0c;输出树的根root&#xff0c;孩子最多的结点max以及他的孩子。 【输入】 第一行&#xff1a;n&#xff08;结点个数≤100&#xff09;&#xff0c;m&#xff08;边数≤200&#xff09;。 以下m行&#xff1a;每行两个结点x和y&#xff0…
阅读更多...
Hyperledger Fabric测试网络运行官方Java链码[简约版]

Hyperledger Fabric测试网络运行官方Java链码[简约版]

文章目录 启动测试网络使用peer CLI测试链码调用链码 启动测试网络 cd fabric-samples/test-networknetwork.sh的脚本语法是&#xff1a;network.sh <mode> [flag] ./network.sh up./network.sh createChannel在java源码路径下 chmod 744 gradlew vim gradlew :set ffu…
阅读更多...
PostgreSQL技术内幕（九）libpq通信协议

PostgreSQL技术内幕（九）libpq通信协议

libpq通信协议是基于TCP/IP 协议的一套消息通信协议&#xff0c;它允许 psql、JDBC、PgAdmin等客户端程序传递查询给PostgreSQL后端服务器&#xff0c;并接收返回查询的结果。 在这次的直播中&#xff0c;我们为大家介绍了libpq通信协议的实现原理和执行机制&#xff0c;以下内…
阅读更多...
发挥AMS、PMS和WMS在框架层服务作用，简化开发过程

发挥AMS、PMS和WMS在框架层服务作用，简化开发过程

Framework底层服务是Android操作系统提供的一组核心服务和功能&#xff0c;用于支持应用程序的开发和运行。这些底层服务提供了许多功能和特性&#xff0c;帮助开发者构建稳定、高效和功能丰富的Android应用程序。 Framework底层服务作用&#xff1a; 管理应用程序的生命周期…
阅读更多...
小白到运维工程师自学之路 第五十一集 （三剑客之sed）

小白到运维工程师自学之路 第五十一集 （三剑客之sed）

一、概述 sed是一个流式文本编辑器&#xff0c;可以对文本进行搜索、替换、删除等操作。它是一个非交 互式的命令行工具&#xff0c;通常用于处理大量的文本数据。sed的工作方式是逐行读取输入文 本&#xff0c;按照预定义的命令对每一行进行处理&#xff0c;并输出结果。它…
阅读更多...
[Linux] 最基础简单的线程池 及其 单例模式的实现

[Linux] 最基础简单的线程池 及其 单例模式的实现

本篇文章主要用到线程相关内容, 下面是博主关于线程相关内容的文章: [Linux] 线程同步分析&#xff1a;什么是条件变量&#xff1f;生产者消费者模型是什么&#xff1f;POSIX信号量怎么用&#xff1f;阻塞队列和环形队列模拟生产者消费者模型 [Linux] 线程互斥分析: 多线程的问…
阅读更多...
Python接口自动化测试--requests高级进阶

Python接口自动化测试--requests高级进阶

Cookies与会话对象 如果某个响应中包含一些Cookie&#xff0c;你可以快速访问它们&#xff1a; import requests r requests.get(http://www.google.com.hk/) print(r.cookies[NID]) print(tuple(r.cookies)) 要想发送你的cookies到服务器&#xff0c;可以使用 cookies 参…
阅读更多...
xShell中使用vim编辑时，无法粘贴外来文本

xShell中使用vim编辑时，无法粘贴外来文本

鼠标右键弹出菜单时&#xff0c;vim直接变成了视图模式了&#xff0c;不能粘贴了。。 好&#xff0c;执行命令 vim ~/.vimrc输入: set mousec即可。 此时便可以粘贴了。
阅读更多...
「观察者（Observer）」设计模式 Swift实现

「观察者（Observer）」设计模式 Swift实现

这里写目录标题 介绍设计模式介绍举例 iOS 中已有的 观察者设计模式实现Notification什么是通知机制或者说如何实现通知机制&#xff1f; KVOKVO底层实现如何实现手动KVO&#xff1f; 介绍 设计模式介绍 观察者设计模式&#xff08;Observer Pattern&#xff09;是一种行为型…
阅读更多...
win10电脑出现网络问题时，如何解决？

win10电脑出现网络问题时，如何解决？

我们的Windows可能会出现各种网络连接问题&#xff1a; 尝试连接Wi-Fi网络时出现错误&#xff1a;Windows无法连接到此网络&#xff1b;您可以通过Wifi访问互联网&#xff0c;但通过电缆访问以太网却无法正常工作&#xff1b;尝试通过电缆连接互联网时出现错误&#xff1a; Wi…
阅读更多...
图数据库：neo4j学习笔记

图数据库：neo4j学习笔记

参考资料&#xff1a;neo4j 教程_w3cschool Springboot集成Neo4j_喝醉的咕咕鸟的博客-CSDN博客 SpringBoot 整合 Neo4j_springboot neo4j_$懒小猿$的博客-CSDN博客 图数据库Neo4j实战&#xff08;全网最详细教程&#xff09;_neo4j使用教程_星川皆无恙的博客-CSDN博客 代码片段…
阅读更多...
Flink DataStream之输出数据到File中

Flink DataStream之输出数据到File中

新建类 package test01;import org.apache.flink.api.common.serialization.SimpleStringEncoder; import org.apache.flink.configuration.Configuration; import org.apache.flink.configuration.MemorySize; import org.apache.flink.connector.file.sink.FileSink; import…
阅读更多...
Model, ViewModel, EnvironmentObject 的使用

Model, ViewModel, EnvironmentObject 的使用

1. Model 数据模型的定义与使用 1.1 案例 struct UserModel: Identifiable{let id: String UUID().uuidStringlet dispalyName: Stringlet userName: Stringlet followerCount: Intlet isVerified: Bool }/// 数据模型 struct ModelBootcamp: View {State var users:[Use…
阅读更多...
web 禁用 OPTIONS方法启用【原理扫描】

web 禁用 OPTIONS方法启用【原理扫描】

Web服务器上启用了HTTP OPTIONS方法。 OPTIONS方法提供了Web服务器支持的方法列表&#xff0c;它表示对有关由Request-URI标识的请求/响应链上可用的通信选项的信息的请求。 直接在IIS上进行关闭即可&#xff1a;
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023