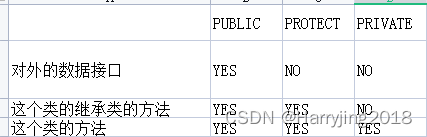
让我们回忆一下共同趋势模型。给定两个时间序列和
,我们有
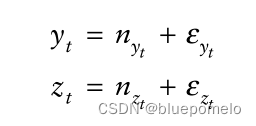
其 中和
是随机游走,即非平稳部分,或者说共同趋势部分(common trends)。
以及
是平稳的部分,即特定部分(specific component)。如果两个时间序列是协整的, 那么他们的共同趋势部分某种程度上(按照一定的比例)是相同的。,即
。
是协整系数。让我们看看共同趋势模型的一些含意:
推论1:如果两时间序列是协整的,那么从共同趋势部分得到的新息序列(innovations sequence)必须是完全相关(即相关系数是或者
)。
从两个时间序列的共同趋势部分得到的新息序列用以及
表示。新息序列表示为:
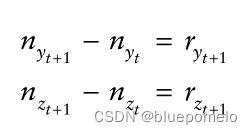
根据在协整系统中,共同趋势部分某种程度上(按照一定的比例)是相同的,即
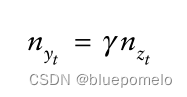
如果我们也要求,
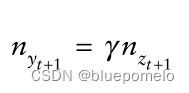
那么,
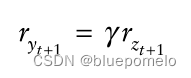
也就是说得到的新息序列某种程度上(按照一定的比例)是相同的,而且这个比例恰好也是协整系数。如果两个变量按照一定的比例相同,那么他们必定是完全相关的,如果协整系数是正的,那么相关系数是+1,如果协整系数是负的,那么相关系数是-1。
推论2:协整系数可以通过两个时间序列的共同趋势的新息序列相互之间的回归得到。
根据推论1,我们有,
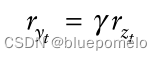
因此,可以通过对一个新息序列与另一个进行简单回归来获得协整系数。因此,协整系数如下
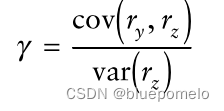
我们要注意两种相关性,即以及
的相关性(从共同趋势部分得到的新息序列)。还有就是完整的时间序列
以及
的相关性。
对于两个协整的时间序列,他们的共同趋势部分可以是平稳的,也可以是非平稳的,没啥特殊的限制。但是对于特定部分(specific component),需要它是平稳的。言外之意,特定部分的一阶差分一定不是白噪声,因为如果差分序列是白噪声,那么特定序列将是随机游动,即非平稳序列。这违反了特定部分必须是平稳的条件。因此,特定部分的一阶差分不能是白噪声。
总结,在共同趋势模型中,协整需要满足两个条件。首先,从共同趋势部分得到的新息序列某种程度上(按照一定的比例)是相同的。其次,两个时间序列的特定部分必须是平稳的。如果要把共同趋势模型应用到股票中,要把时间序列分成两部分,即非平稳的部分/共同趋势部分以及平稳的部分/特定部分。这样的话,我们需要用到套利定价理论APT,建立共同趋势模型与APT之间的联系。