文章目录
- 题目
- 1.错误示范
- 2. 分析
- 逆序对的判断
- 统计出某个数后面有多少个数比它小
- 举例(完整过程解析)
- 第一次循环
- 第二次循环
- 第三次循环
- 第四次循环
- 第五次循环
- 循环结束的两种存在情况
- 3. 正确代码
- 4.递归展开图
题目
1.在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
示例 1:
输入: [7,5,6,4]
输出: 5
1.错误示范
int reversePairs(int* nums, int numsSize) {
int i = 0;
int j = 0;
int sum = 0;
for (i = 0; i < numsSize; i++)
{
for (j = i + 1; j < numsSize; j++)
{
if (nums[i] > nums[j])
{
sum++;
}
}
}
return sum;
}
我们用正常的思路去写,发现就会超出时间限制,因为这样做 时间复杂度为O(N^2),很显然不符合条件
2. 分析
从归并排序(递归)中,可知 ,我们可以通过临时数组tmp 先排序左数组
再排序右数组,最后将左右数组进行排序
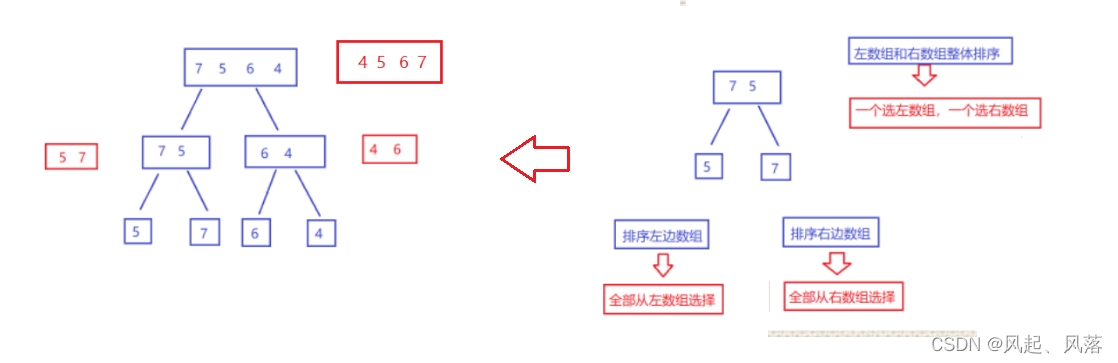
而这三种情况,正好对应 逆序对中的 全部从左数组选择、 全部从右数组中选择。 一个选左数组一个选右数组
逆序对的判断
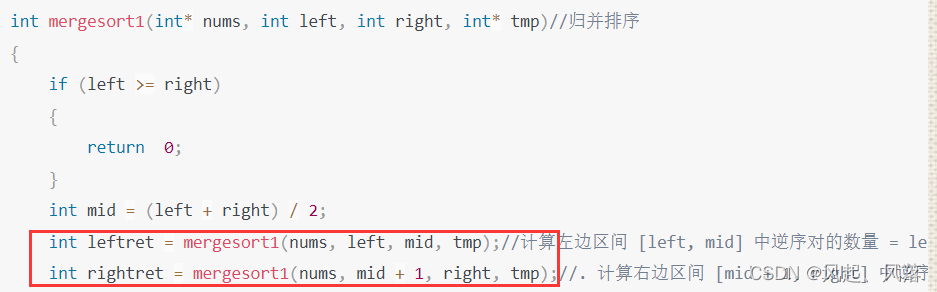
全部从左数组选择、 全部从右数组中选择,我们只需加上返回值即可
统计出某个数后面有多少个数比它小
在归并合并的过程中,可以 得到两个有序的数组,通过有序性快速统计出你逆序对的数量
举例(完整过程解析)
假定left与right数组有序
left=[5,7,9] right=[4,5,8] tmp=[]
第一次循环
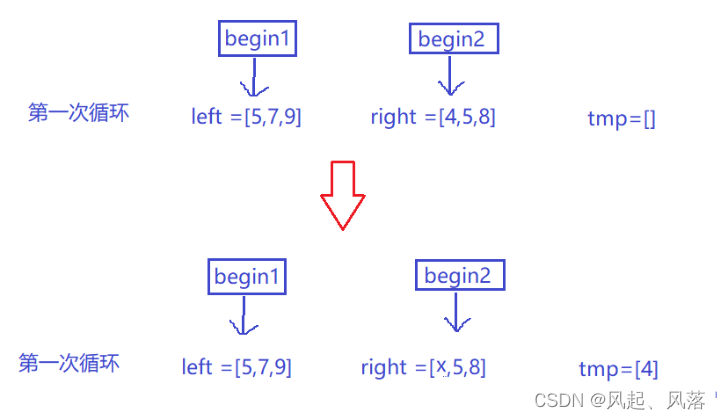
left[begin1] (5)>right[begin2] (4) ,将 right[begin2]放入tmp数组中,并将begin2++
由于是 升序排列, 所以left数组第一个必是最小的数,而这个最小的数比right所取的数大,则right所取的数(4)比left数组中所有数都小,即为tmp进入排序的第一个数
由于4<5,我们要统计 在right数组中有多少数比5小,所以 begin2++
第二次循环
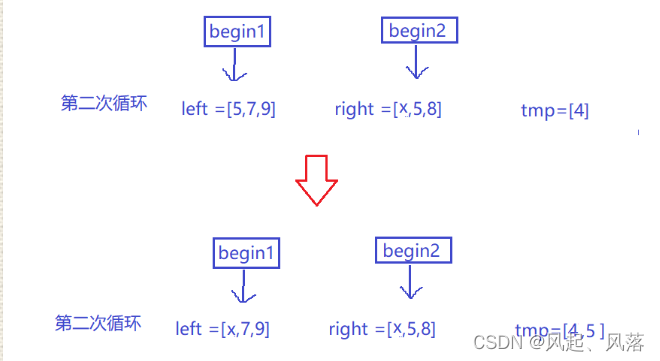
left[begin1] (5) <= right[begin2] (5) 将left[begin1] 放入 tmp数组中 ,并将 begin1++
最小的数已经放入tmp数组中,此时left[begin1] (5) 就是次小的数 即tmp数组中的第二个数
此时在right数组中 [0,begin2)区间的数 都比left[begin1] (5) 小
即 ret += begin2-0
left[begin1] (5) 已经找到>=它的数,begin1++ 遍历下一个left数组中的数
第三次循环
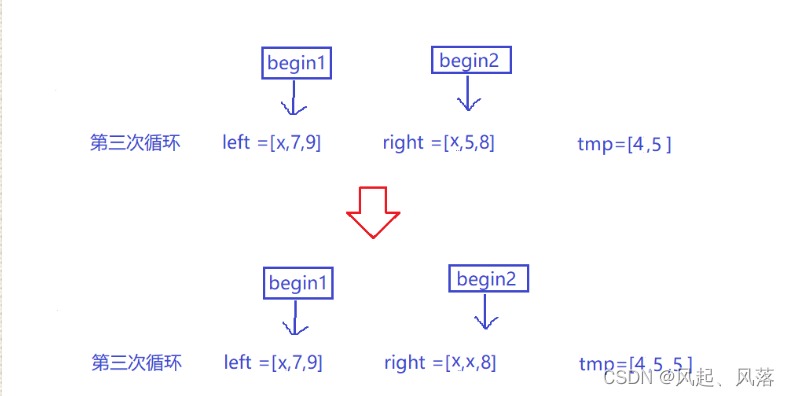
left[begin1] 1(7) > right [beign2] (5) 将right[begin2] 放入tmp数组中,并将begin2++
在剩余的数中,由于7>5 ,所以 5就为目前最小的数 ,将其放入 tmp数组中
同时7也没有找到>= 它的数,所以需要 beign2++
第四次循环
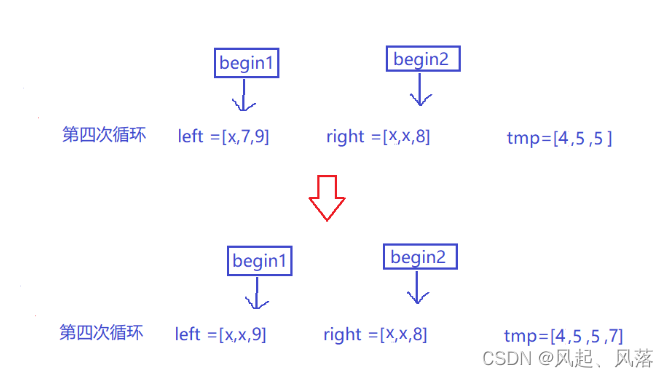
left[begin1] (7) < right[begin2] (8) 将left[begin1] 放入tmp数组中,并将begin1++
在剩余的数中,由于 7<8 ,所以 7就为目前最小的数 ,放入tmp数组中
此时 right数组[0,beign2)区间 小于7
ret+=begin2-0
left[begin1] (7) 已经找到>=它的数,将 begin1++ ,遍历下一个 left数组中的数
第五次循环
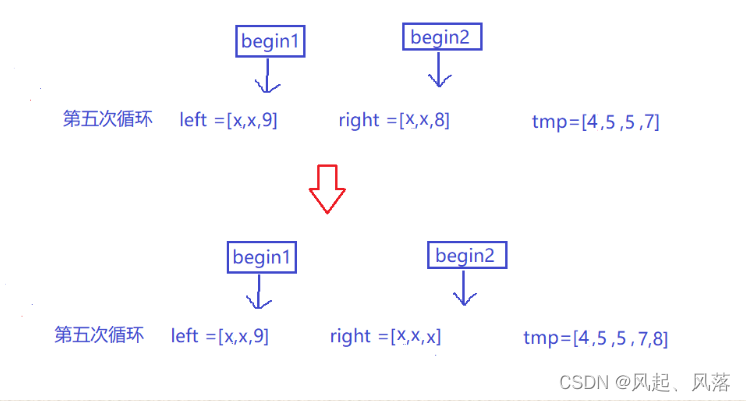
left[begin1] (9) > right[begin2] (8) 将right[begin2]放入tmp数组中,并将begin2++
在剩余的数中,由于 8<9 ,所以 8就为目前最小的数 ,放入tmp数组中
同时begin2++ ,继续寻找right数组中是否存在>=9的数
循环结束的两种存在情况
由于right数组已经遍历完,所以循环停止,再次判断两个数组是否存在数
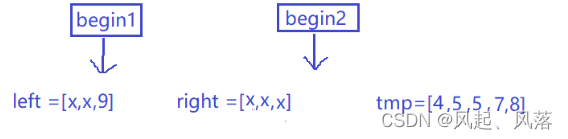
若 left数组没有走完,则left剩余的每一个数 都 > 原right数组存在的数
right数组区间[0,begin2) 正好为 right数组的所有数
所以还需累加 ret+= begin2-0
若 right数组没有走完,题中要求为逆序对,即左边大于右边的数,
不成立,所以不用统计无意义
3. 正确代码
int mergesort1(int* nums, int left, int right, int* tmp)//归并排序
{
if (left >= right)
{
return 0;
}
int mid = (left + right) / 2;
int leftret = mergesort1(nums, left, mid, tmp);//计算左边区间 [left, mid] 中逆序对的数量 = leftRet,并排序;
int rightret = mergesort1(nums, mid + 1, right, tmp);//. 计算右边区间 [mid + 1, right] 中逆序对的数量 = rightRet,并排序
int begin1 = left;
int end1 = mid;
int begin2 = mid + 1;
int end2 = right;
int i = left;
int voeret = 0;//合并左右两个有序区间,并且计算逆序对的数量
while (begin1 <= end1 && begin2 <= end2)
{
if (nums[begin1] <= nums[begin2])
{
//当 nums[begin1] <= nums[begin2] 时,说明此时右边数组已经遍历过的元素都是比
// nums[begin1] 小的,因此累加到 voeret 中去
voeret += begin2 - (mid + 1);//因为计算的begin2刚开始的边界就为 mid+1
tmp[i++] = nums[begin1++];
}
else
{
//当 nums[begin1] > nums[begin2] 时,无需统计,直接归并
tmp[i++] = nums[begin2++];
}
}
//处理归并排序中剩余的元素;
//当左边有剩余的时候,还需要统计逆序对的数量;
//当右边还有剩余的时候,无需统计,直接归并。
while (begin1 <= end1)
{
voeret += begin2 - (mid + 1);
tmp[i++] = nums[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = nums[begin2++];
}
memcpy(nums + left, tmp + left, sizeof(int) * (right - left + 1));
return leftret + rightret + voeret;//返回 左区间逆序对数量 + 右区间逆序对数量 + 当前合并过程中产生的逆序对数量
}
int mergesort(int* nums, int numsSize)
{
int* tmp = (int*)malloc(sizeof(int) * numsSize);//因为我们不想一直malloc创建数组所以在外面开辟
int ret = mergesort1(nums, 0, numsSize - 1, tmp);
free(tmp);
tmp = NULL;
return ret;
}
int reversePairs(int* nums, int numsSize) {
return mergesort(nums, numsSize);
}
4.递归展开图
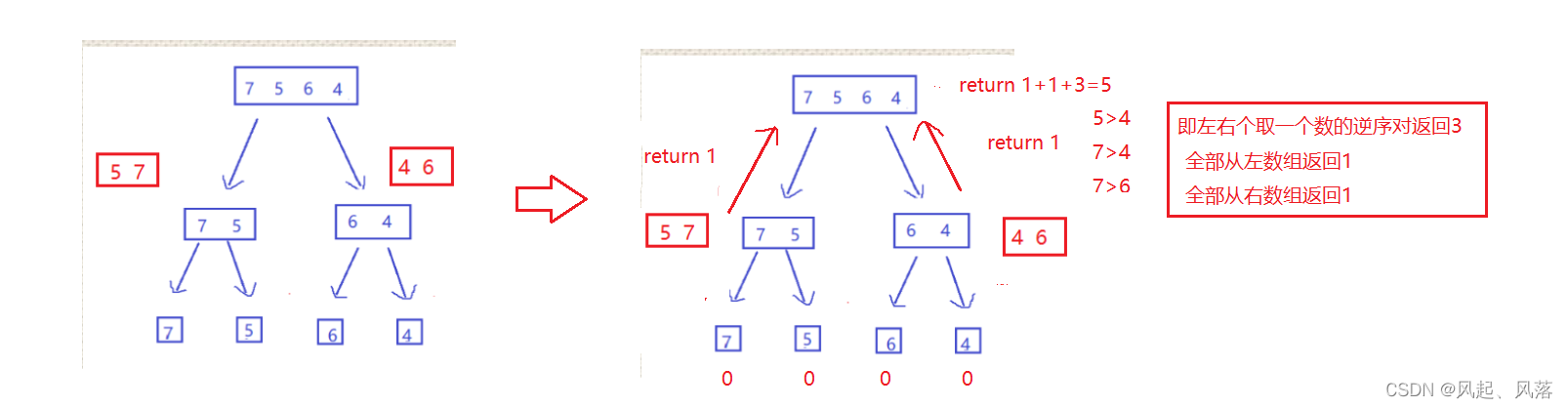
以下标从0到3 的数组进行演示