持续了十期的《计算之魂》主题周赛告一段落,可能上周就已经告一段落了,以致于也出现了重复的考题。这本书确实不错,里面提到的计算机思维我认为是理解和学习计算机科学的基础。第一次读此书的时候就一口气读到第八章,读到精彩之处,不禁拍案叫绝。在此也强烈推荐对计算机、算法感兴趣的朋友都能读到这本书。
本期周赛换了个主题,说实话我是不懂这本书的。

从比赛中的选择题来看,貌似是和数据库以及大数据有关? 所幸四道选择题没什么难度,手机度娘一下就有答案。——这也是我一直觉得把非编程题放进周赛不妥的地方,考察的东西要么不太公平,(并不是所有人都了解数据库),要么就很容易从网上搜到答案(那考它还有什么意义?)
按你胃,作为一种以练代学的形式,周赛放进更贴合学生人群考试会用到的选择、填空等题型,也是可以理解的,不必过多纠结。
下面说说本期两道编程题。
看到题目的时候,我就大概想到这两道题会被不少人吐槽。不是指题目的难度,而是题目的数据输入形式。我们分别来看。
第一题:覆盖面积
给你二维平面上两个 由直线构成且边与坐标轴平行/垂直 的矩形,请你计算并返回两个矩形覆盖的总面积。 每个矩形由其 左下 顶点和右上顶点坐标表示: 第一个矩形由其左下顶点 (ax1, ay1) 和右上顶点 (ax2, ay2) 定义。 第二个矩形由其左下顶点 (bx1, by1) 和右上顶点 (bx2, by2) 定义。 参数限制: -10e4 <= ax1, ay1, ax2, ay2, bx1, by1, bx2, by2 <= 10e4
题目说得还算比较明白,但是这四个坐标点、八个参数是什么形式输入的呢?
再看题目给出的两个示例:

你一定以为是一行字符串?甚至脑海中马上想到要先对其进行复杂的字符串处理,提取出八个代表坐标的数字。。。
然鹅, 输入的八个数字实际上是分行录入的,一行一个数字,共八行,而且除了数字,并没有其他乱七八糟的等号、逗号等字符。惊不惊喜?
而当你怀着这种惊喜来看第二题的时候,
第二题:机器猫
小光买了一个可编程机器猫,机器猫初始位置在原点(0, 0)。 小伙伴事先给机器猫输入一串指令command,机器猫就会无限循环这条指令的步骤进行移动。指令有两种: U: 向y轴正方向移动一格 R: 向x轴正方向移动一格。 D: 向y轴负方向移动一格 L: 向x轴负方向移动一格。不幸的是,在 xy 平面上还有一些遮挡物,他们的坐标用 barriers 表示。机器猫一旦碰到遮挡物就会被损毁。 限制: 2 <= command的长度 <= 1000 command由 U,R,D,L构成(个数不限制) 0 <= x <= 1e9 0 <= y <= 1e9 0 <= barriers 的长度 <= 1000 barriers[i]不为原点或者终点
给出的输入数据是这种形式:

有了第一题的经验,这题自然可以想到不用去考虑变量名、等号、逗号之类。没错,的确是输入四行,每行一个变量值。但是第二个变量,barriers的值直接给出的是 [[4,2]] 这样的字符串。意不意外?
当然,使用 Python 处理这样的字符串,可以直接通过 eval() 函数将其一步转换成列表,但是用其它语言的童鞋就不知道有没有好的处理办法了。我有理由怀疑一些之前的比赛好手,以及大多数选手,都是因为这个原因花了不少时间,甚至卡住都有可能。
本期两道编程题数据输入部分极不规范,也没有描述数据输入的形式,是最大的bug。
如果你解决了数据输入的问题,那这两道题本身实际上并没有什么难点。下面我也简单说说我的理解。
第一题题解
解法一:
用暴力穷举模拟的方法就可以通过此题(因为数据量太弱)。我们都知道“点多成面”,坐标系里的矩形,实际上是由该矩形空间里的点组成,而每个点又都可以用坐标表示。比如,矩形(0,0, 2, 2)包含了 (0, 0),(0, 1),(1, 0),(1, 1) 这四个点。而该矩形的面积是4,正好等于点的数量。注意:矩形其中两条边上的点是不包含的。——这是比较基础的数学计数问题,类似于0到9虽然有10个数,但是0到9的距离是9。
所以,我们就可以暴力地构建两个矩形集合,把矩形内的所有坐标点都放进去。然后对这两个集合取并集。其中重复的点,就相当于两个矩形重合的部分,并集操作的时候就自然去重了。最后再统计新的集合里有多少个点,就是总的覆盖面积了。
解法二:
如上所述,暴力穷举法可以通过此题的原因是该题目前的测试数据范围太小,因为它的时间复杂度是 ,n 和 m 分别代表矩形的长和宽。如果该数字变大,很容易就会超时。
实际上,这也是一道数学问题,可以用数学方法的 常数级复杂度来解。
早在去年的时候,我就在问答频道解过类似的题目:Python解数学题-编程语言-CSDN问答
本题也是一样,答案就是两个矩形的面积之和减去相交部分的面积:

我们暂时先考虑两个矩形相交的情况,稍后你会发现不相交的情况其实是相交的变种。
如何得到图中相交部分的长和宽,继而求出面积呢?
进一步分析,不难看出, y 的长度,实际上等于两个矩形顶部较矮(小)的那条边的高度,减去矩形底部较高(大)的那条边的高度。写成公式就是 。
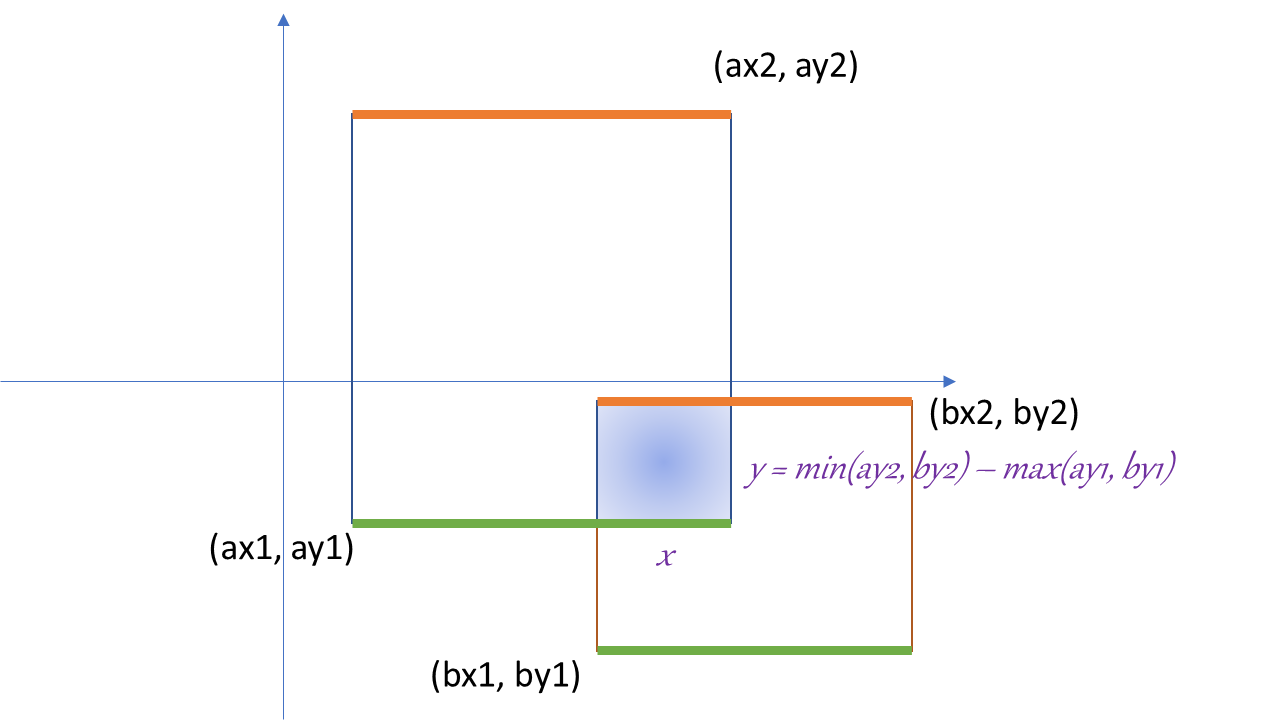
而同理,可得出 x 的长度,等于两个矩形右侧靠左的那条边的位置,减去两个矩形左侧靠右的那条边的位置。

可见,x 和 y 都可以通过已有的变量计算得到。那不相交的情况呢?
我们将上面的矩形水平拉开,就可以看到,通过上面的公式计算出的 x 是会小于 0 的。纵向的 y 也是一样。

于是,我们可以加个判断,或使用 max() 函数,当 x 或 y 小于 0 时,他们的值就取 0 。这样一来,相交部分的面积等于 x * y,如果不相交,那这个计算结果是 0,符合预期。
所以最终答案就是
第二题题解
本题如果解决了上面提到的列表的输入问题,实际上也没有什么难度。而且本题的答案不是 "true" 就是 "false",对于这种只有两个答案的二元题目,面向输入编程(骗分)往往更简单更快。
即使打算认真做,本题只要模拟机器猫的运动轨迹即可,机器猫的初始位置为(0, 0)。因为是不断地循环指令集,每个指令集里又分别有上(U)、下(D)、左(L)、右(R)四个方向的组合,可以设置双循环。外层循环重复读取指令集,内层循环用于读取指令,向相应的方向移动一步。每移动一步就进行判断,是否遇到障碍,还是遇到终点。两种情况都直接退出双循环,前者输出"false",后者输出"true"。
这便是这道题的基本逻辑,甚至逻辑都谈不上,纯粹模拟。
然鹅,如果一直遇不到障碍,也到不了终点呢?理论上应该输入"false",但代码会无限运行下去。简单来说,何时判定终止外层循环呢?
C语言的选手可以设定一个循环时间,超过此时间即输出 "false",也算是个物理外挂。
让我们想想如果真有机器猫这个玩具,在给定的指令集下不断循环移动,在没有障碍物也没碰到终点的情况下,什么时候你会停下它呢?
很显然,当你发现它离终点越来越远的时候——永远不可能到达终点了,你会手动把它停下。
于是,很直观地,我们可以设定一个距离,当这个距离越来越大时,就表示不可能到达终点了。此处,我们使用曼哈顿距离即可。在外层循环加上一个判断,每执行完一次指令集后,判断机器猫的位置到终点的距离,相比上一次是否更远了。如果更远,则直接结束循环,输出 "false",也不用管障碍了(遇到障碍也是 "false",所以不用管)。
注意,这个判断不能加在内循环中,因为每走一步(而不是走完一次指令集),机器猫的位置相对上一次,都有可能更近或更远,并没有判断的意义。只有当执行完一次指令集后,我们才能得到判断:这个指令集会使机器猫更近还是更远。如果从一个更远的地点,执行相同的指令集,得到的结果必然比现在距离终点更远。