方法1: 从前往后进行分析
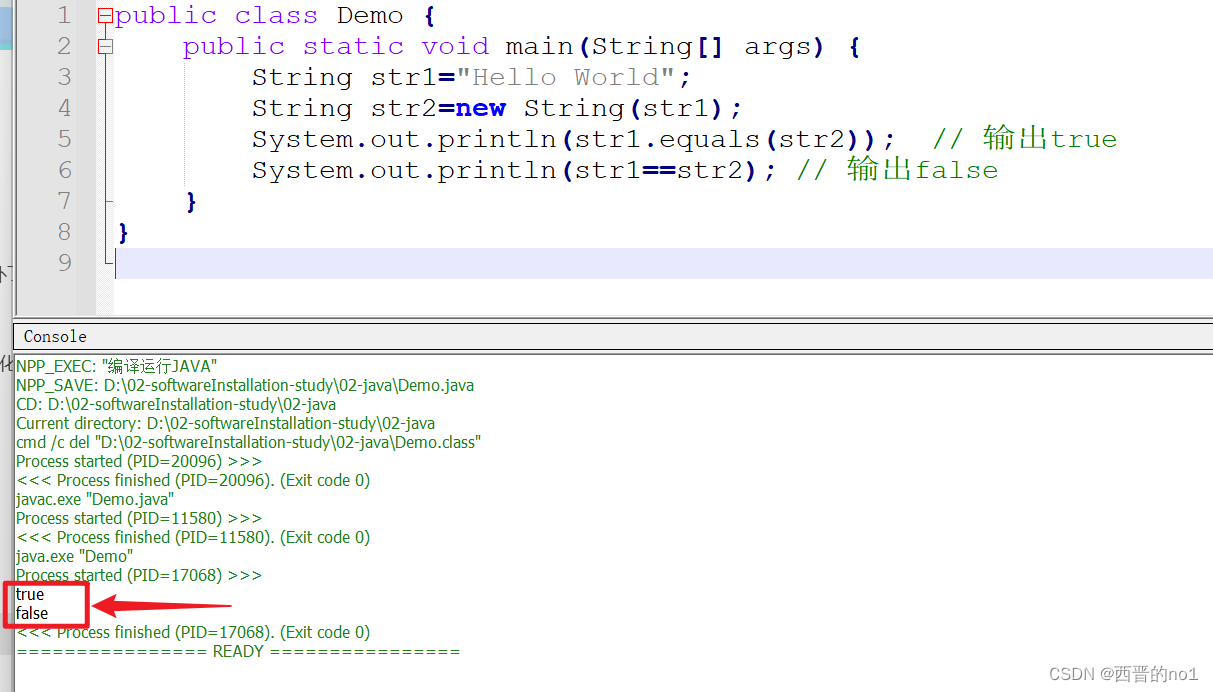
代码展示:
class Solution {
public int minCostClimbingStairs(int[] cost) {
int length = cost.length;
//定义dp数组
int[] dp = new int[length + 1];
//初始化
dp[0] = 0;
dp[1] = 0;
//填充dp数组
for (int i = 2; i <= length; i++) {
dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
//返回值
return dp[length];
}
}以示例1为例,我们爬到下标为0的台阶的最小花费为0,即dp[0]=0
爬到下标为1的台阶的最小花费为0,即dp[1]=0
计算爬到下标为2的台阶的最小花费,我们需要判断是先到下标为0的台阶再到下标为2的台阶还是先到下标为1的台阶再到下标为2的台阶,第一种方式所需要的花费是到下标为0的台阶的最小花费0+下标为0的台阶到下标为2的台阶的花费10=10,第二种方式所需要的花费是到下标为1的台阶的最小花费0+下标为1的台阶到下标为2的台阶的花费15=15,由于要求最小花费,所以我们选择花费少的方法,即dp[2]=10
爬到楼顶的花费同理,我们需要判断是先到下标为1的台阶再到楼顶还是先到下标为2的台阶再到楼顶,第一种方式所需要的花费是到下标为1的台阶的最小花费0+下标为1的台阶到楼顶的花费15=15,第二种方式所需要的花费是到下标为2的台阶的最小花费10+下标为2的台阶到楼顶的花费20=30,由于要求最小花费,所以我们选择花费少的方法,即dp[3]=15
根据以上分析我们可以得到状态转移方程 dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
得到了状态转移方程。接下来定义dp数组,初始化dp数组,填充dp数组,返回值就可以了
方法2:从后往前分析
代码展示:
class Solution {
public int minCostClimbingStairs(int[] cost) {
int length = cost.length;
//定义dp数组
int[] dp = new int[length];
//初始化
dp[length - 1] = cost[length - 1];
dp[length - 2] = cost[length - 2];
//填充dp数组
for (int i = length - 3; i >= 0; i--) {
dp[i] = cost[i] + Math.min(dp[i + 1], dp[i + 2]);
}
return Math.min(dp[0], dp[1]);
}
}以示例1为例,我们从下标n-1的位置到楼顶的最小花费是20,即dp[n-1]=cost[n-1]=20
从下标n-2的位置到楼顶的最小花费是15,即dp[n-2]=cost[n-2]=15
所以我们从n-3的位置到楼顶的最小花费要判断是先到n-1位置再到楼顶,还是先到n-2位置再到楼顶,到n-1位置再到楼顶的花费为cost[n-3]+dp[n-1]=10+20=30;到n-2位置再到楼顶的花费为cost[n-3]+dp[n-2]=25,所以dp[n-3]=min(cost[n-3]+dp[n-1],cost[n-3]+dp[n-2])=min(dp[n-1],dp[n-2])+cost[n-3]
获得了dp[0]=25,dp[1]=15,我们可以选择从台阶0位置出发,也可以选择从台阶1位置出发,所以选择较小的台阶1位置出发,即最小花费为min(dp[0],dp[1])=15
根据以上的分析我们得到了状态转移方程为dp[i]=min(dp[i+1],dp[i+2])+cost[i]
返回的值为min(dp[0],dp[1])