- 基本初等函数的输入
- 系统运算与操作函数的输入
- 函数值的计算
- 1. 数值计算方式
- 2. 符号计算方式
- 2.1 函数:sym
- 2.2 函数:syms
- 函数的作图
- 1. 一般函数 y=f(x) 的作图(二维)
- 作图基本形式
- 作多重线
- 作图的线型和颜色
- 作图的网格和标记、图例、字号
基本初等函数的输入
在 MATLAB 中,函数输入的总体原则是 将变量整体用括号括起来。
如
c
o
s
2
x
3
cos2x^3
cos2x3 的 MATLAB 输入为
c
o
s
(
2
∗
(
x
3
)
)
cos(2*(x^3))
cos(2∗(x3)),
x
3
x^3
x3 本来不需要用括号括起来,但括起来后,运算次序更加清晰。

系统运算与操作函数的输入
在 MATLAB 中,通常以由基本初等函数扩展的数学函数作为处理的对象。
此外,MATLAB 系统还设计了具有运算和操作性质方面的函数,它们常作为处理的工具。这类函数常见的有以下几种:
- 绝对值函数 ∣ x ∣ |x| ∣x∣ : a b s ( x ) abs(x) abs(x)
- 符号函数 s i g n x signx signx : s i g n ( x ) sign(x) sign(x)
- 求和函数: s u m sum sum
- 求积函数: p r o d prod prod
- 求最大值: m a x max max
- 求最小值: m i n min min
函数值的计算
- 在数学运算中,运算的结果如果是一个 数值,可以称这类运算为 数值运算;
- 如果运算结果为 表达式,在
MATLAB中称为 符号运算,符号计算是对 未赋值的符号对象 (可以是常数、变量、表达式)进行运算和处理。
在符号运算中是以表达式形式呈现结果的,而在数值运算中是以数值表示结果的。
1. 数值计算方式
>>x=… %输入 x 的数值(不能为字母)
>>y=… %输入 y 的表达式(表达式中除 x 外不能有其他字母)
【例题1】设
y
=
3
x
2
−
2
3
x
+
2
x
3
−
4
e
2
x
y=3x^2- \frac{2}{3^x}+\frac{2^x}{3}-4e^{2x}
y=3x2−3x2+32x−4e2x,用 MATLAB 计算
y
(
1
)
y(1)
y(1) 的值。
MATLAB 程序如下:

【例题2】设
y
=
{
x
2
+
1
,
x
<
0
2
x
−
1
,
0
<
x
≤
10
2
x
+
3
,
x
>
10
y = \begin{cases} x^2 + 1, & x < 0 \\ 2^x - 1, & 0<x \leq 10 \\ 2x+3, & x > 10 \end{cases}
y=⎩
⎨
⎧x2+1,2x−1,2x+3,x<00<x≤10x>10 用 MATLAB 计算
y
(
5
)
y(5)
y(5) 的值。
MATLAB 程序如下:

【注意】elseif 中的 else 与 if 之间不能空格,否则要用两个 end。

2. 符号计算方式
建立符号变量的方法有两种,通常
- 用
sym建立单个符号对象, - 用
syms同时定义多个符号对象。
2.1 函数:sym
功能:用来建立 单个 符号对象。
a = sym('a'); %定义符号变量 a,下同
b = sym('b')
c = sym('c')
d = sym('d') %至此定义了 4 个符号变量

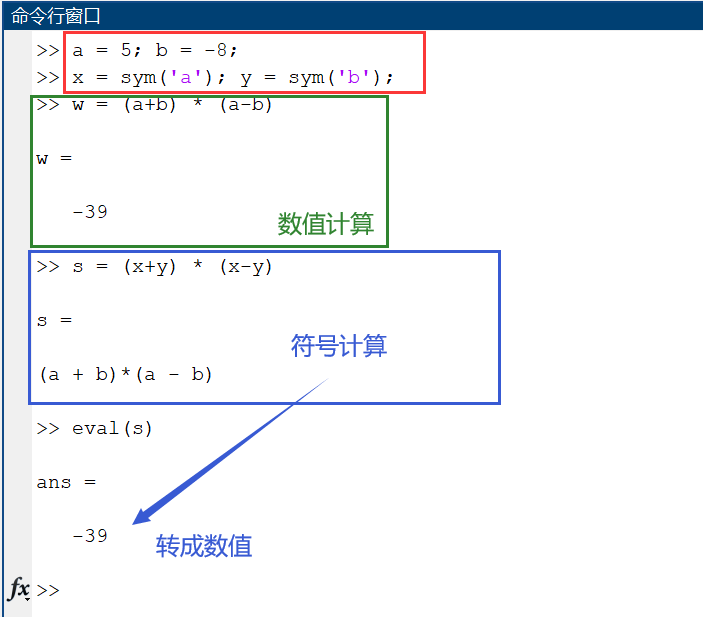
由以上例子可以看出:
- 符号计算 的结果是一个 表达式。
- 数值计算 的结果是一个 数值。
2.2 函数:syms
功能:定义 多个 符号对象。
syms x y z %同时定义 x,y,z 为符号变量
>>syms x 其他字母 %定义 x 和其他字母为符号
>>y=f(x); %输入 y 的表达式
>>subs(y,x,a) %计算 x=a 时 y 的值
【注意】
- 如果要计算在 多个点 x = a 1 , … , x = a n x=a_1,…,x=a_n x=a1,…,x=an 处 y y y 的值,则可用 [ a 1 , a 2 , … , a n ] [a_1,a_2,…,a_n] [a1,a2,…,an] 替换 a a a,即 s u b s ( y , x , a ) subs(y,x,a) subs(y,x,a) 改为 s u b s ( y , x , [ a 1 , a 2 , . . . , a n ] ) subs(y,x,[a_1,a_2,...,a_n]) subs(y,x,[a1,a2,...,an])。
- 如果结果
“ans=”是以 符号形式 给出时,输入 d o u b l e ( a n s ) double(ans) double(ans) 即可得到 数值型结果。
【例题1】设
y
=
3
l
n
x
2
−
l
o
g
2
x
⋅
l
o
g
10
(
3
x
)
+
1
2
l
o
g
3
(
4
x
)
y=3lnx^2-log_2x · log_{10}(\frac{3}{x})+\frac{1}{2}log_3(4x)
y=3lnx2−log2x⋅log10(x3)+21log3(4x) ,用 MATLAB 计算
y
(
1
)
y(1)
y(1)、
y
(
2
)
y(2)
y(2) 的值。
MATLAB 程序如下:
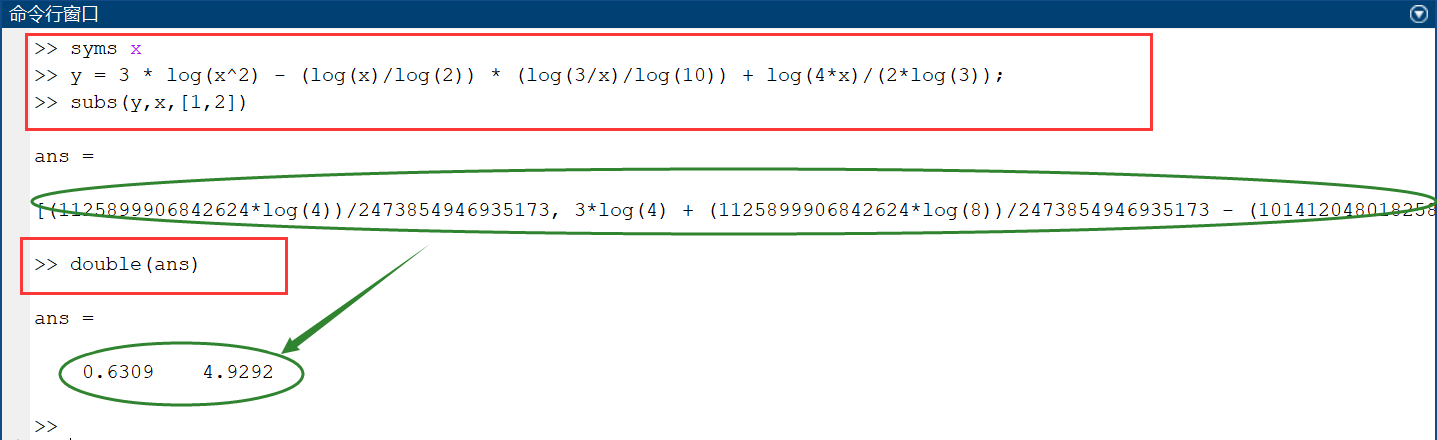
试验 l o g 2 x log_2x log2x 和 l o g 10 x log_{10}x log10x 不用换底公式,得到的结果同上。
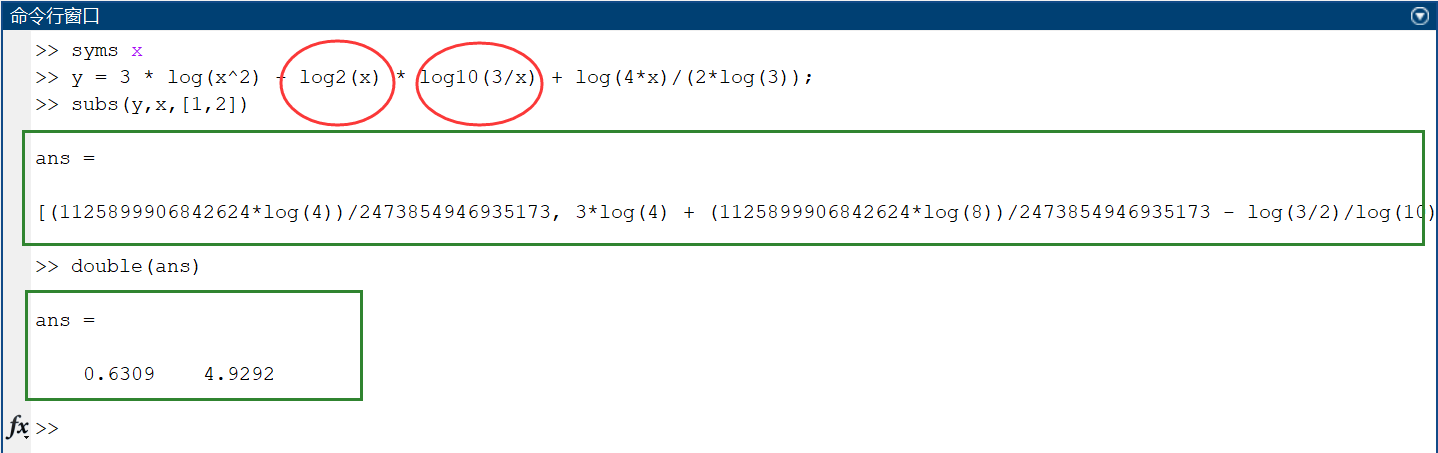
【例题2】设
y
=
x
2
−
2
a
x
y=x^2-2ax
y=x2−2ax,用 MATLAB 计算
y
(
a
)
y(a)
y(a)、
y
(
b
)
y(b)
y(b) 的值。
MATLAB 程序如下:
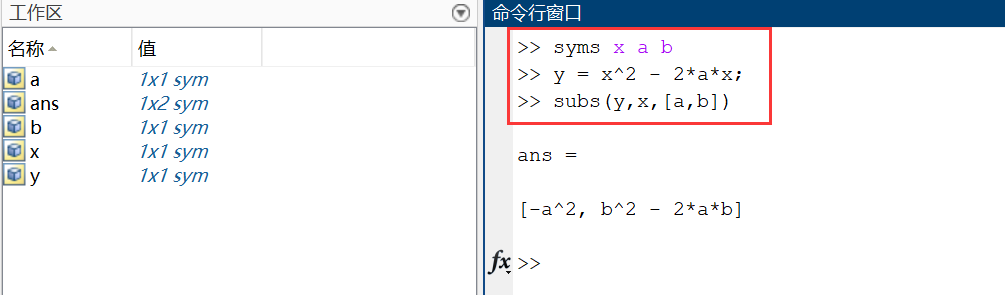
【注意】用 符号计算方法 时,相关式子中的所有字母都要先定义为符号,其运算结果依然是一个 符号表达式。
函数的作图
MATLAB 有很强的图形功能,可以方便地实现 数据的视觉化。下面着重介绍二维图形的画法。
1. 一般函数 y=f(x) 的作图(二维)
作图基本形式
二维图形的绘制是 MATLAB 语言图形处理的基础,MATLAB 最常用的画二维图形的命令是 plot,MATLAB 命令格式:
>>x=a:c:b %输出 x 的范围[a,b],步长为 c
>>y=f(x); %输出 y 的表达式
>>plot(x,y) %画出函数的图像
plot- 二维线图
此MATLAB函数 创建Y中数据对X中对应值的二维线图。 要绘制由线段连接的一组坐标,请将X和Y指定为相同长度的向量。
要在同一组坐标区上绘制多组坐标,请将X或Y中的至少一个指定为矩阵。向量和矩阵数据 plot(X,Y) plot(X,Y,LineSpec) plot(X1,Y1,...,Xn,Yn) plot(X1,Y1,LineSpec1,...,Xn,Yn,LineSpecn) plot(Y) plot(Y,LineSpec)
【例子】

生成的图形如下图所示,是 [ 0 , 2 π ] [0, 2π] [0,2π] 上 30 个点连成的光滑的正弦曲线。
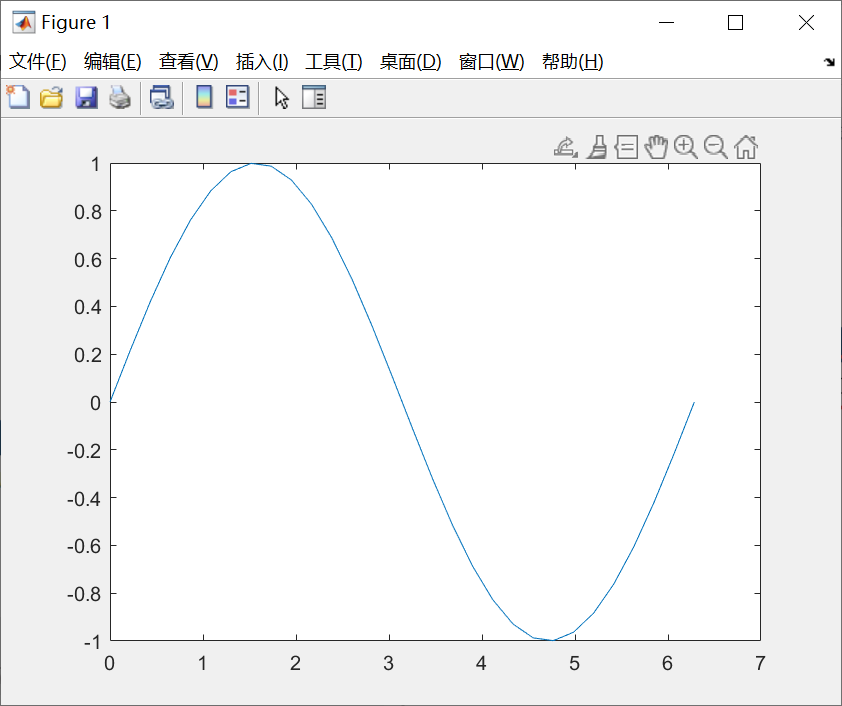
关于 linspace 的说明文档如下:

作多重线
在 同一个画面上可以画许多条曲线,只需多给出几个数组,MATLAB 命令程序格式:
>>x=a:c:b
>>y1=f(x); y2=g(x);
>>plot(x, y1, x, y2) %在同一平面画出两个函数的图像
【例子】

则可以画出下图:
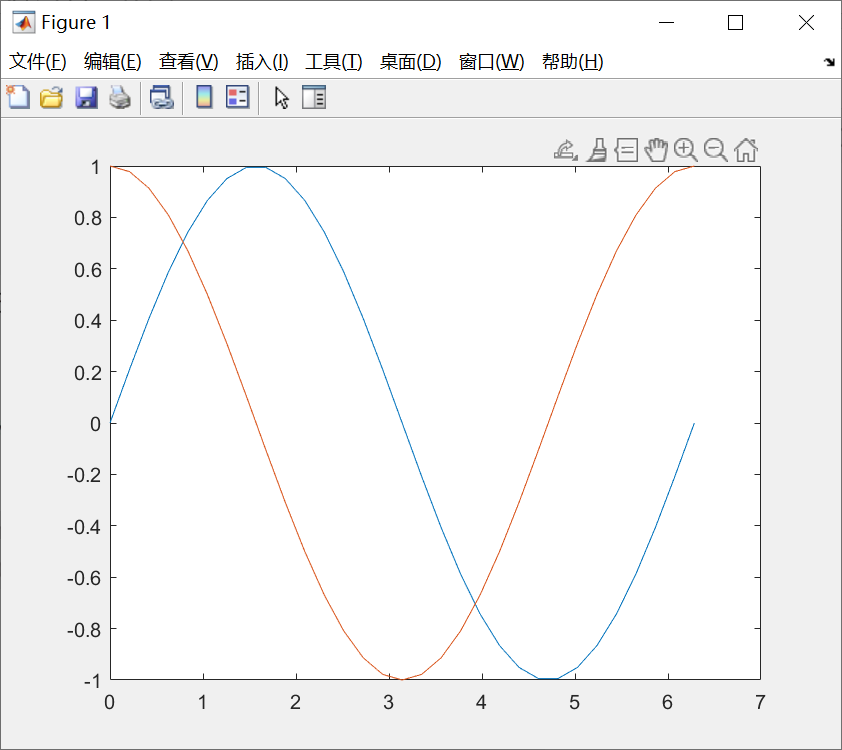
【注意】
- 也可用
hold on语句,达到作多重图的效果,MATLAB命令格式:
>>plot(表达式 1, [a,b])
>>hold on
>>plot(表达式 2, [a,b])
- 如果要在一个画布上作
k个小图,则可用subplot(m, n, k),MATLAB命令格式:
>>subplot(m, n, k);
>>fplot(表达式 1, [a, b])
即表达式 1 所表示的曲线画在 m 行 n 列第 k 个位置上(从左至右,再从上至下计数)。
作图的线型和颜色
为了适应各种绘图需要,MATLAB 提供了用于控制线色、数据点和线型的 3 组基本参数。它的使用格式如下:plot(x, y, color_point_linestyle)

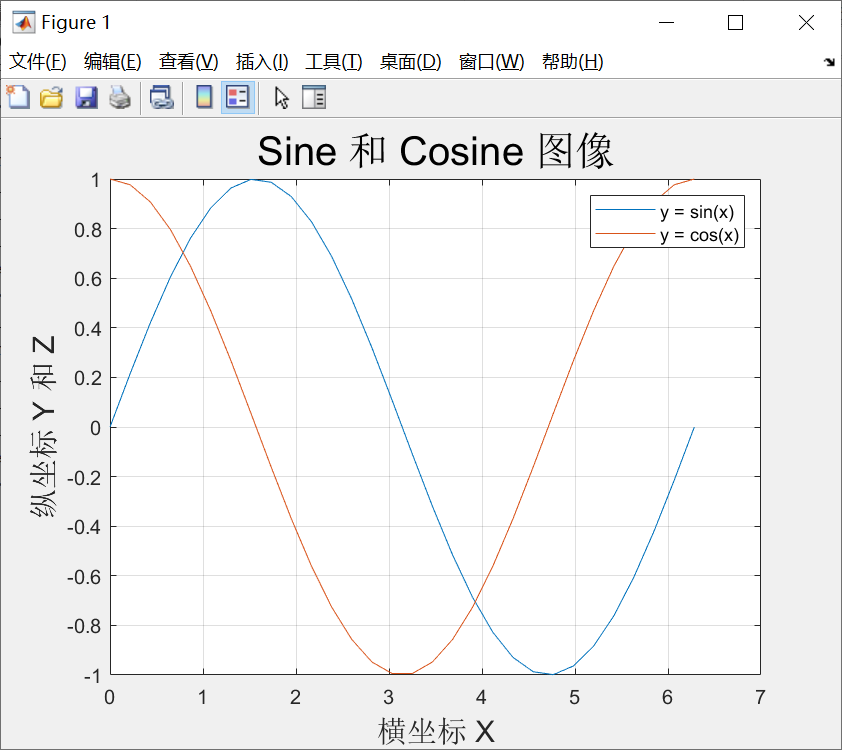
作图的网格和标记、图例、字号
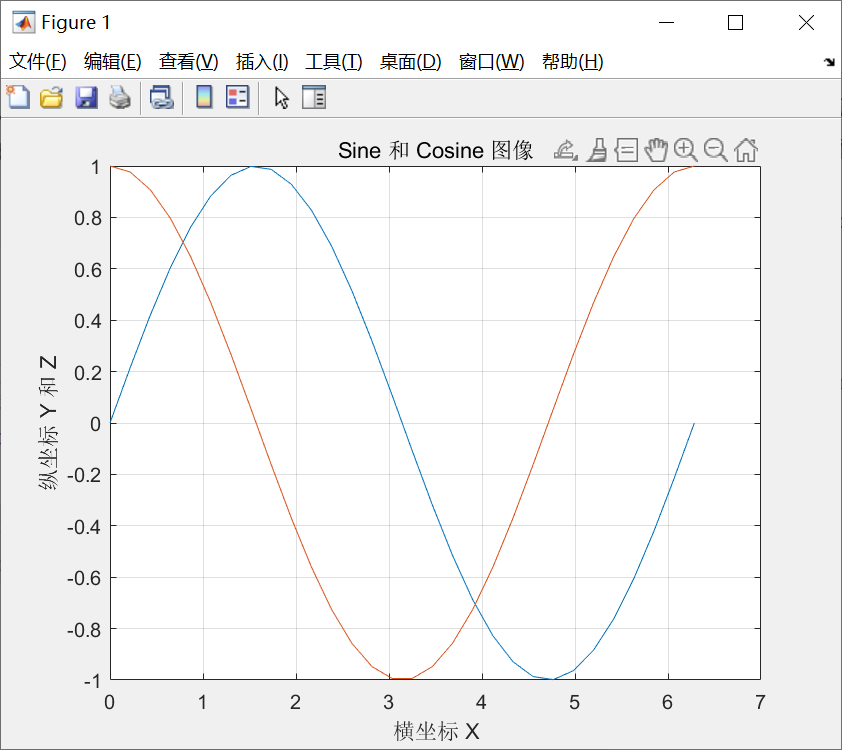
在一个图形上可以加网格、标题、x 轴标记、y 轴标记,用下列命令完成这些工作。
x=linspace(0, 2*pi, 30); y=sin(x); z=cos(x);
plot(x, y, x, z)
grid %网格
xlabel('横坐标 X') %横坐标标签
ylabel('纵坐标 Y 和 Z') %纵坐标标签
title('Sine 和 Cosine 图像') %标题
【注意】 shift + Enter 换行且不执行。

效果如下图:
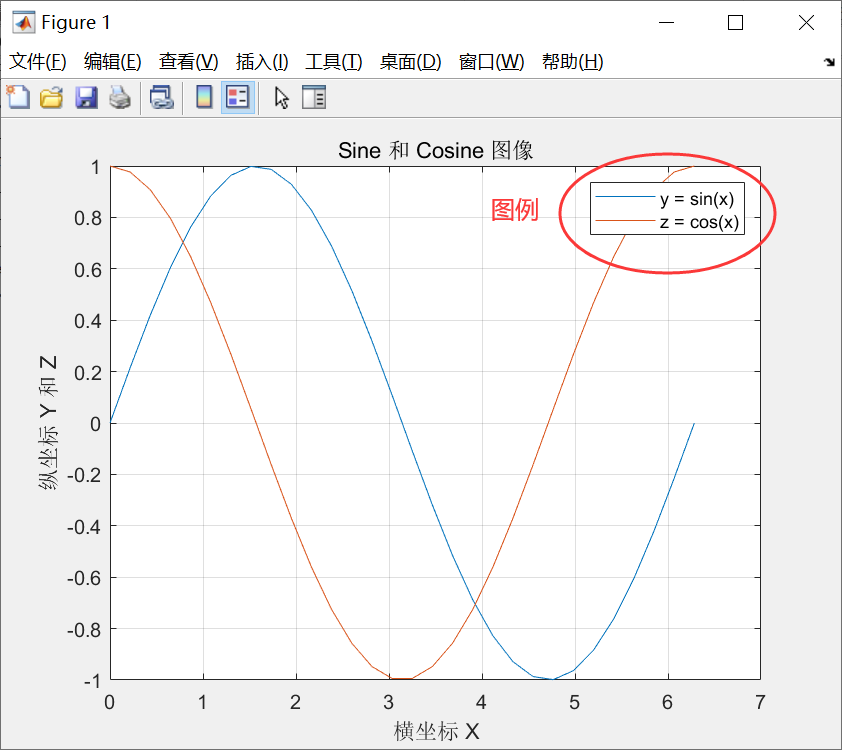
【添加图例】
legend:按绘图顺序添加图例。
x=linspace(0, 2*pi, 30); y=sin(x); z=cos(x);
plot(x, y, x, z)
grid %网格
xlabel('横坐标 X') %横坐标标签
ylabel('纵坐标 Y 和 Z') %纵坐标标签
title('Sine 和 Cosine 图像') %标题
% 按绘图顺序添加图例
legend('y = sin(x)','y = cos(x)')
【限制画布】
如果限制画布,则需在输入 plot 语句前输入 >>axis([a, b, c, d]),这个命令是将图形限制在
[
a
,
b
]
×
[
c
,
d
]
[a,b]×[c,d]
[a,b]×[c,d] 上,其中
a
a
a,
b
b
b,
c
c
c,
d
d
d 必须是数值。
【'FontSize' 字号属性】
x=linspace(0, 2*pi, 30); y=sin(x); z=cos(x);
plot(x, y, x, z)
grid %网格
xlabel('横坐标 X','FontSize',15) %横坐标标签
ylabel('纵坐标 Y 和 Z','FontSize',15) %纵坐标标签
title('Sine 和 Cosine 图像','FontSize',20) %标题
legend('y = sin(x)','y = cos(x)')