二叉树的定义

在数据结构中，二叉树是n（n>=0）个节点的有限集，它或者是空集（n=0），或者由一个根节点及两棵互不相交的分别称为左子树和右子树。二叉树通常用于实现搜索和排序算法，同时也可以用于存储表达式和计算表达式的值等应用场景。
完全二叉树：
除了最后一层节点可以不满，其他层节点都必须是满的，最后一层的节点从左到右依次排列,如上左图就是完全二叉树
满二叉树：
除了叶子节点，每个节点都有两个子节点。
特点：
1、每个节点最多有两个孩子（二叉树中不存在度大于2的节点）。
2、子树有左右之分，其次序不能颠倒。
3、二叉树可以是空集合，根可以有空的左子树或者空的右子树。
注意二叉树不是树的特殊情况，他们是两个概念。
在这里插入图片描述

二叉树的5种基本形态

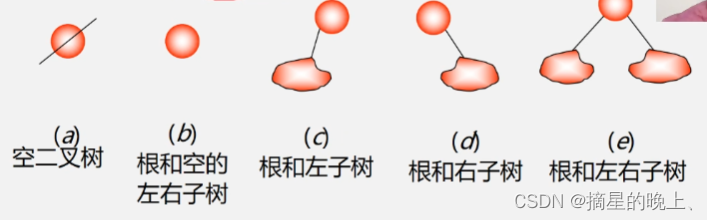
在这里插入图片描述

二叉树的抽象类型定义

CreateBiTree(&Tdefinition)
初始条件：definition给出二叉树T的定义。
操作结果：按definition构造二叉树T。
PreOrderTraverse(T)
初始条件：二叉树T存在。
操作结果：先序遍历T，对每个结点访问一次。
InOrderTraverse(T)
初始条件：二叉树T存在。
操作结果：中序遍历T，对每个结点访问一次。
PostOrderTraverse(T)
初始条件：二叉树T存在。
操作结果：后序遍历T，对每个结点访问一次。
在这里插入图片描述

二叉树的特殊类型

完全二叉树：
除了最后一层节点可以不满，其他层节点都必须是满的，最后一层的节点从左到右依次排列。叶子只能分布在最大的两层上面。

满二叉树：
除了叶子节点，每个节点都有两个子节点，深度为k的满二叉树，有2的k次幂-1个节点。叶子结点都在最底层。
在这里插入图片描述
满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。

二叉树的性质

二叉树的存储结构

1、顺序存储

按照顺序存储结构的二叉树节点数值如下：
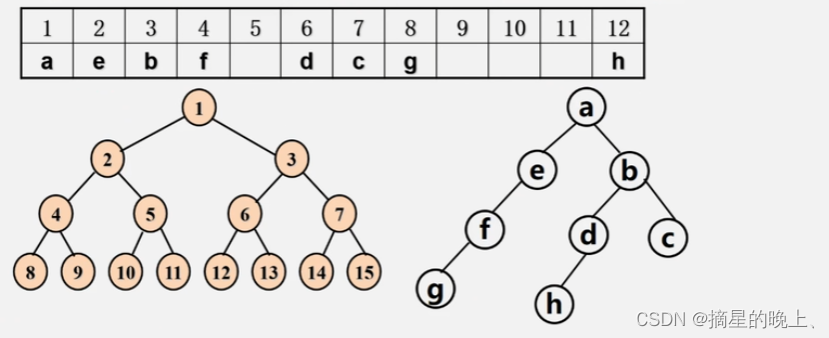
在这里插入图片描述

2、链式存储

链式存储结构的二叉树如下：
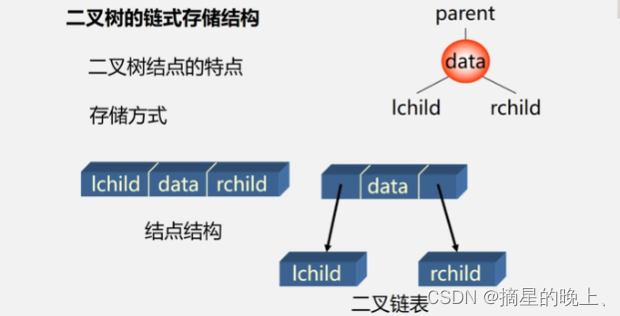
在这里插入图片描述

在这里插入图片描述
实现：

struct BTreeNode{
	elemType data;
	struct BTreeNode *left, *right;  // 左右孩子指针
};

遍历二叉树

二叉树的遍历是指从二叉树的根结点出发，按照某种次序依次访问二叉树中的所有结点，使得每个结点被访问一次，且仅被访问一次。
1、LDR 中序遍历：左子树—》根节点—》右子树
2、DLR 前序遍历：根节点—》左子树—》右子树
3、LRD 后序遍历：左子树—》右子树—》根节点

前序遍历

定义
前序遍历通俗的说就是从二叉树的根结点出发，当第一次到达结点时就输出结点数据，按照先向左在向右的方向访问。
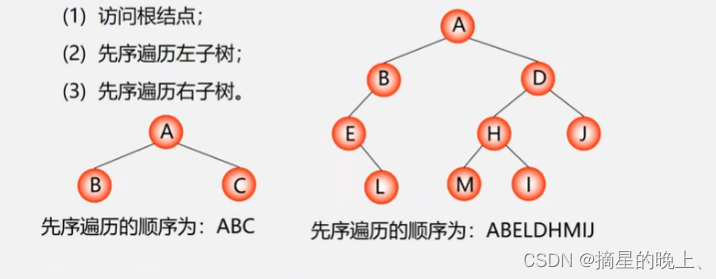
在这里插入图片描述

中序遍历

定义
中序遍历就是从二叉树的根结点出发，当第二次到达结点时就输出结点数据，按照先向左在向右的方向访问。
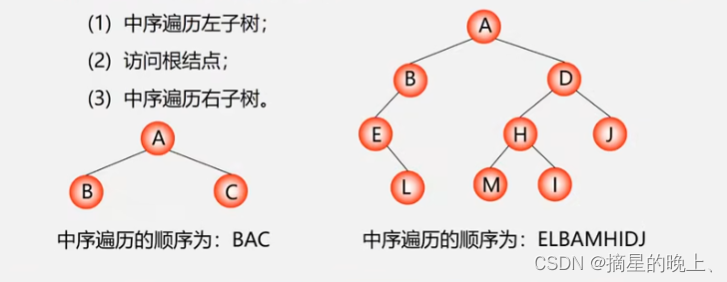
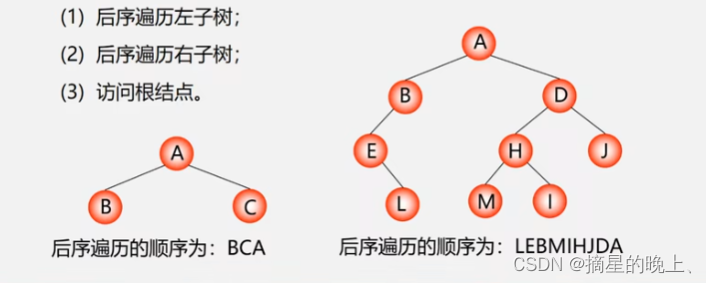
在这里插入图片描述

后序遍历

定义
后序遍历就是从二叉树的根结点出发，当第三次到达结点时就输出结点数据，按照先向左在向右的方向访问。
在这里插入图片描述

注意：
已知前序遍历序列和后序遍历序列，不可以唯一确定一棵二叉树。
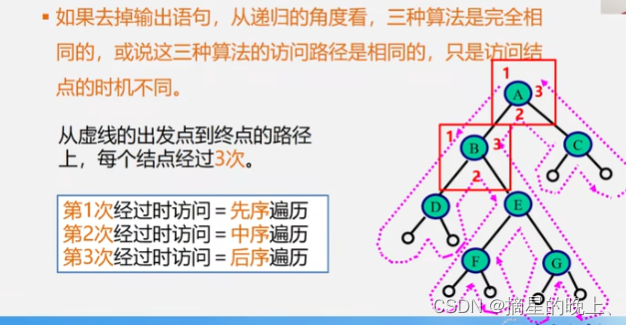
在这里插入图片描述

遍历算法的分析

在这里插入图片描述
时间效率：O(n) // 每个节点只访问一次
空间效率：O(n) // 栈占用的最大辅助空间

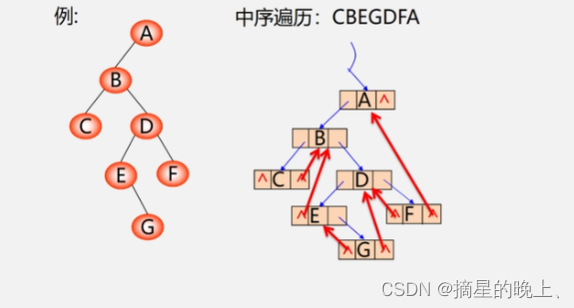
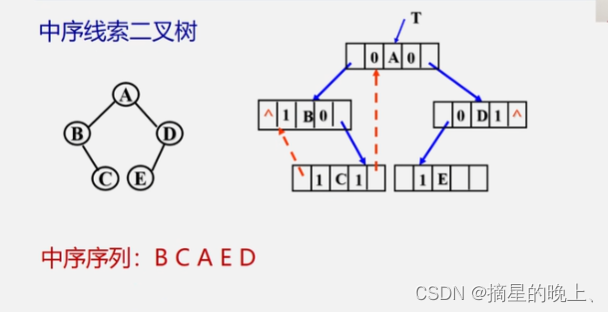
线索二叉树

如果某个结点的左孩子为空，则将空的左孩子指针域改为指向其前驱;如果某结点的右孩子为空，则将空的右孩子指针域改为指向其后继，这种改变指向的指针称为“线索”
加上了线索的二叉树称为线索二叉树(Threaded Binary Tree)。
对二叉树按某种遍历次序使其变为线索二叉树的过程叫线索化。
在这里插入图片描述