图源:文心一言
Chat GPT生成,代码的核心思想与王道咸鱼老师的视频虽然类似,但是在具体实现上毕竟还是略有差别~~因此,如果对考研方向的并查集代码感兴趣,可以查看——
王道咸鱼老师的视频:{5.5_2_并查集_哔哩哔哩_bilibili}
Pecco大佬的博文:算法学习笔记(1) : 并查集 - 知乎 (zhihu.com)
第1版:查资料、画导图、画配图~🧩🧩
参考用书:王道考研《2024年 数据结构考研复习指导》
特别感谢: Chat GPT老师、文心一言老师、BING AI老师~
📇目录
目录
📇目录
🦮思维导图
🧵基本概念
⏲️定义
⌨️代码实现
🧵分段代码
🔯P0:调用库文件
🔯P1:定义数组存储变量
🔯P2:初始化
🔯P3:查询元素的根结点
🔯P4:合并集合
🔯P5:查询结点是否在同一集合
🔯P6:main函数
🧵完整代码
🔯P0:完整代码
🔯P1:执行结果
🔚结语
🦮思维导图
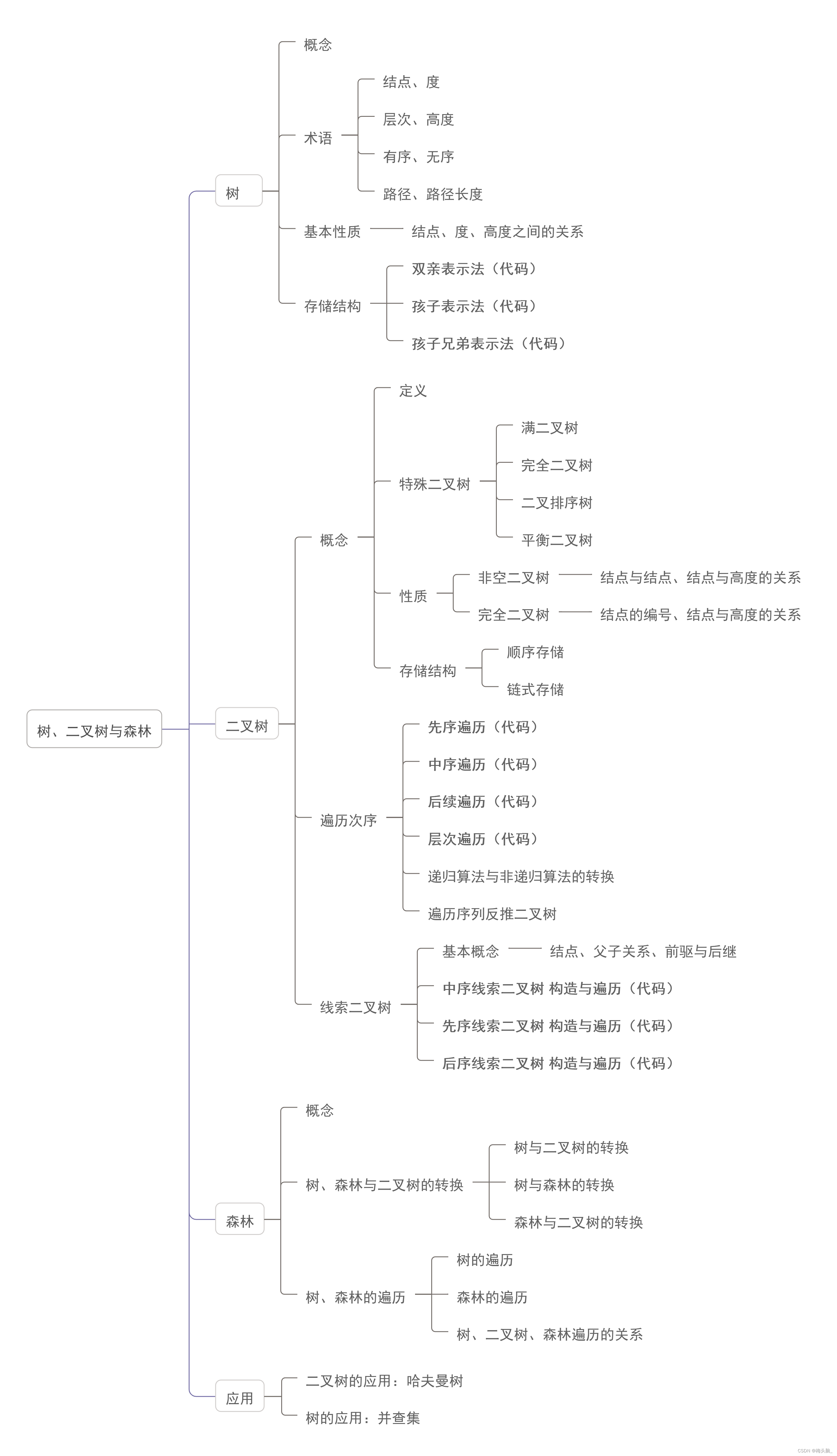
备注:
- 思维导图为整理王道教材第5章 查找的所有内容;
- 本篇仅涉及到哈夫曼树HuffmanTree的代码;
- 本章节往期博文,涉及到树与二叉树的内容如下~
- 🌸[树:双亲、孩子、兄弟表示法][二叉树:先序、中序、后序遍历]
- 🌸数据结构05:树与二叉树[C++][线索二叉树:先序、中序、后序]
- 🌸数据结构05:树与二叉树[C++][哈夫曼树HuffmanTree]
🧵基本概念
⏲️定义
首先,让我们来了解一下并查集是什么。并查集是一种可以维护一些元素之间等价关系的数据结构。说得直白一点,就是可以用来管理一些“兄弟关系”。
并查集的核心操作:查找和合并。(1)查找操作就像是问某个过路人:“请问你是他兄弟吗?”(2)而合并操作就像在说:“以后我们就是兄弟了!”
- 查找(Find):查找元素所属的集合,即找到该集合的代表元素。通过递归或迭代,可以找到代表元素。
- 合并(Union):将两个集合合并成一个集合。首先找到两个集合的代表元素,然后将其中一个集合的代表元素指向另一个集合的代表元素。
并查集的优化技巧:路径压缩和按秩合并。(1)路径压缩就像是一个人在寻找他的老大时,叫上自己所有的兄弟,堵在家族大佬的门口。(2)而按秩合并则像是一个家族中的老大,他把一些小弟合并到自己的家族中,这样可以保证家族的规模不会太大,从而优化查询和合并的效率。
- 路径压缩(path compression):在查找操作 find 中,通过将当前节点的父节点设置为根节点来压缩路径。这样可以使得树的高度变得更小,从而加快后续查找操作的速度。
- 按秩合并(union by rank):在合并操作 unite 中,通过根据集合的大小(秩)决定合并方向,将较小的集合合并到较大的集合上。这样可以避免将较大的树合并到较小的树上,从而保持整体树的平衡性,减少查找操作的平均时间复杂度。
以上的举栗可能过于抽象,且术语可能过于拗口。下面我们以代码+配图的方式说明如何创建并查集~

图源:文心一言
⌨️代码实现
🧵分段代码
🔯P0:调用库文件
- 输入输出流文件iostream{用于输入与输出};
- 动态数组的向量文件vector{用于创造元素的集合};
#include <iostream>
#include <vector>🔯P1:定义数组存储变量
- 向量parent:存储元素的父结点;
- 向量size:存储以当前结点为根结点的子集合数量;
备注:个人还是习惯把向量叫做动态数组,因为实现的逻辑确实与动态的数组很类似~
std::vector<int> parent; // parent数组 用于存储每个元素的父节点
std::vector<int> size; // size数组 用于存储每个集合的大小,即集合中元素的数量🔯P2:初始化
- 向量parent初始化:长度为在main函数中定义的长度,每个元素的值为1,表示当前结点的子集合数量为n;
- 向量size初始化:长度为在main函数中定义的长度,每个元素的值为自身,表示当前结点的父结点为自身;
说明1:执行的效果大概如下图所示~

说明2:
- size初始化为1,是因为此时的结点没有从属关系,每个结点都没有孩子;
- parent初始化为自身,可能与后面介绍的find函数使用路径压缩频繁递归调用自身有关~
UnionFind(int n) { // 初始化并查集,长度为n
parent.resize(n); // 定义 parent数组长度为n
size.resize(n, 1); // 定义 size数组长度为n,每个元素的值为1
for (int i = 0; i < n; ++i) { // 定义 parent数组的父结点为自身
parent[i] = i;
}
}🔯P3:查询元素的根结点
这段代码的功能是查询某个集合内的祖先结点,核心是“parent[x] = find(parent[x]);”:
- 若仅执行 find(parent[x]); 会递归查询父结点,可以完成查询功能,不会改变树的结构,是最最常规的操作~
- 若执行 parent[x] = find(parent[x]); 会递归查询父结点,不仅可以完成查询功能,而且会将本结点祖先们的父结点{parent}都修改为树的根结点的值~
这样做,由于会调整树形,因此本次查询的操作时间实际会略微增长,但是在下次查询时的次数就会变短~
我们举个栗子,在一棵瘦树上查找结点3:

- 左侧是普通查询:查询结点3每次都会是3次;
- 右侧是压缩路径:查询结点3第1次是3次{同普通查询},然后将路径上的点都挂在根结点下,之后每次查询结点3{甚至是同路径上的结点2、结点1}都会是1次~
int find(int x) { // 查询集合的根
if (x != parent[x]) { // 若{查询的元素 ≠ 父结点}
parent[x] = find(parent[x]); // 递归调用本函数,将本函数到根结点路径上的所有结点都挂在最末端的结点(即根结点)下
}
return parent[x]; 说实话,这段代码我理解了很久,因为涉及到递归调用栈,因此像我一样有点迷糊的同学可以替换成下面这段代码进行测试——
int find(int x) {
std::cout << "传入参数find(x=" << x << ")" << std::endl;
if (x != parent[x]) {
std::cout << "parent[x]=" << parent[x] << ", x != parent[x]" << std::endl;
parent[x] = find(parent[x]);
std::cout << "将结点" << x << "的parent设置为结点" << parent[x] << std::endl;
} else {
std::cout << "parent[x]=" << parent[x] << ", x == parent[x]" << std::endl;
std::cout << "返回parent[x] = " << parent[x] << std::endl;
}
return parent[x];
}
就会很清楚地看到栈是怎么运行的~

🔯P4:合并集合
这段代码的功能是传入两个元素x、y,使用找到两个集合的根rootx、rooty{在寻找的过程中调用了find函数,因此也会执行路径压缩的操作},然后将小树{元素更少的树}合并到大树{元素更多的树}下~
为什么这样合并呢?因为树的层数直接决定了查找与合并的效率。如果频繁地把大树合并到小树的下面,那么这棵树肯定会倾向于又瘦又高,不利于我们执行频繁的查询操作~
void unite(int x, int y) { // 合并集合
int rootX = find(x); // 寻找x元素所在集合的根 rootx
int rootY = find(y); // 寻找y元素所在集合的根 rooty
if (rootX != rootY) { // 若{两个集合的根不等}
if (size[rootX] < size[rootY]) { // 若{集合x的元素数量 < 集合y的元素数量}
parent[rootX] = rootY; // 将x元素的祖先结点rootx 挂在 y元素的祖先结点rooty 的后代位置
size[rootY] += size[rootX]; // 集合y的元素数量 = 集合y的元素数量 + 集合x的元素数量
} else { // 若不满足{集合x的元素数量 < 集合y的元素数量}
parent[rootY] = rootX; // 将y元素的祖先结点rooty 挂在 x元素的祖先结点rootx 的后代位置
size[rootX] += size[rootY]; // 集合x的元素数量 = 集合x的元素数量 + 集合y的元素数量
}
}
}🔯P5:查询结点是否在同一集合
这段代码的功能是传入两个元素x、y,使用找到两个集合的根rootx、rooty{在寻找的过程中调用了find函数,因此也会执行路径压缩的操作}:根结点相同则在同一个集合内~
void isConnected(int x, int y) { // 查询是否为同一集合
if (find(x) == find(y)){ // 若{x元素所在集合的根 = y元素所在集合的根}
std::cout << x << "与" << y << "属于同一集合" << std::endl; // 输出x与y属于同一集合
}else{ // 若不满足{x元素所在集合的根 = y元素所在集合的根}
std::cout << x << "与" << y << "不属于同一集合" << std::endl; // 输出x与y不属于同一集合
}
}🔯P6:main函数
main函数除了P0~P5的函数调用,就创建了3棵小树,进行了并、查操作,如果我没有理解错,完整的过程应该是这样的~
- 第1步:设定数组元素、初始化;
- 第2步:经过元素合并{main函数从合并(0,6)执行到合并(2,5)},创建如图所示的3棵小树,注意创建时,尺寸size数组和父结点parent数组都会更改~

- 第3~4步:合并(4,8)(2,9)即将3棵树合并为1棵大树,如果不执行路径压缩与按秩合并,结果应该是下面这样的;

根据上图的话,如果查询根结点,结点1、3、5都会查询1次, 结点0、4、9都会查询2次, 结点0、4、9都会查询3次,平均下来就是平均每个结点查询2次~
- 第3~4步:合并(4,8)(2,9)即将3棵树合并为1棵大树,如果执行路径压缩与按秩合并,结果应该是下面这样的;
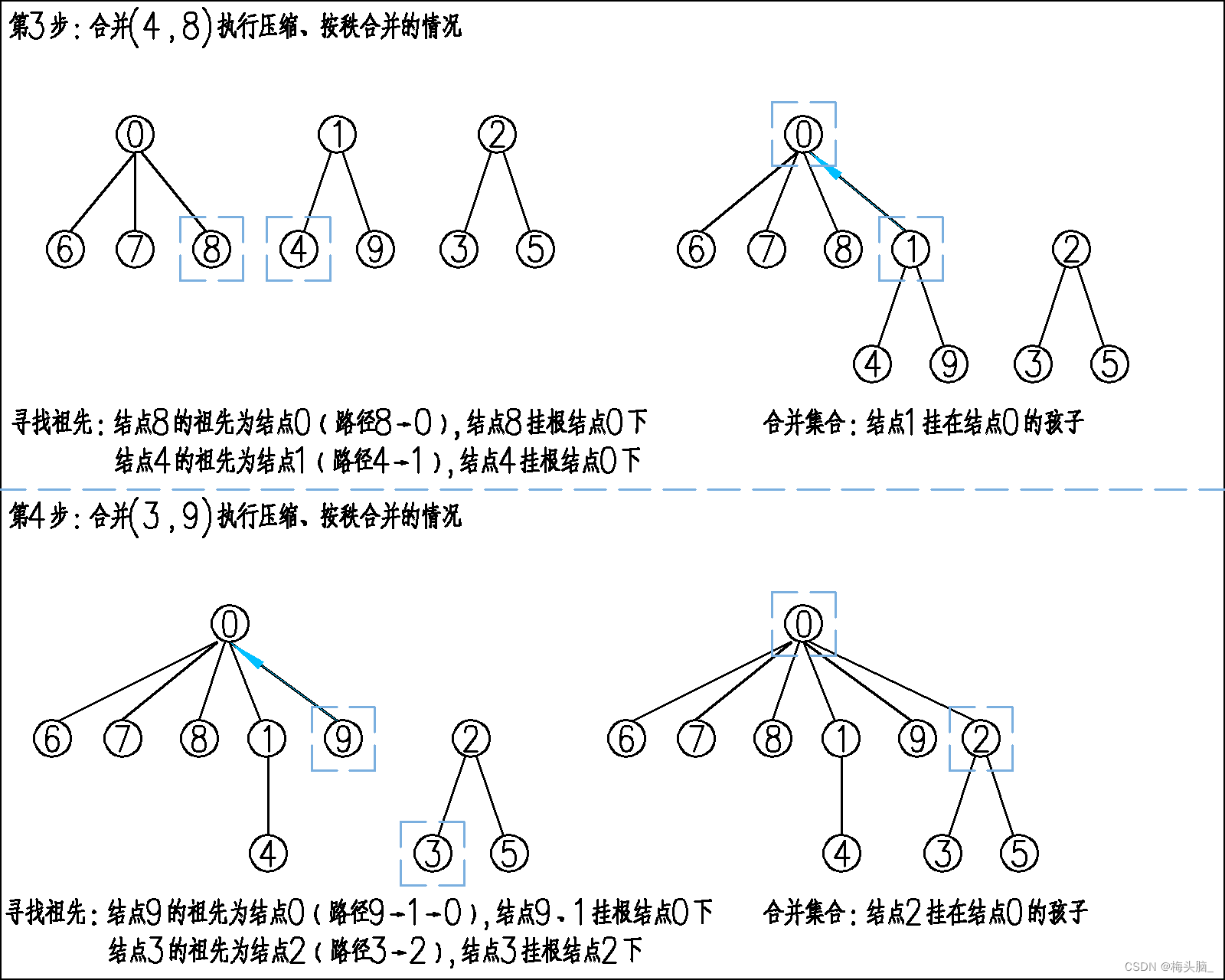
根据上图的话,如果查询根结点,结点6、7、8、1、9、2都会查询1次, 结点4、3、5都会查询2次,平均下来就是平均每个结点查询1.3次~
相比不优化,平均每个结点节省了35%的效率~当然如果元素越多,节省的查询效率也就越多哦~
int main() {
int n = 10; // 设置数组共有10个元素
UnionFind uf(n); // 初始化
uf.unite(0, 6); // 合并集合{0,6}
uf.unite(0, 7); // 合并集合{0,7}
uf.unite(0, 8); // 合并集合{0,8}
uf.unite(1, 4);
uf.unite(1, 9);
uf.unite(2, 3);
uf.unite(2, 5);
// uf.isConnected(0, 6); // 输出 0,不属于同一个集合
// uf.isConnected(0, 9); // 输出 1,属于同一个集合
uf.unite(4, 8); // 合并集合{8,1}
uf.unite(3, 9); // 合并集合{3,9}
uf.isConnected(0, 5); // 输出 1,属于同一个集合
return 0;
}🧵完整代码
🔯P0:完整代码
为了凑本文的字数,我这里贴一下整体的代码,删掉了细部注释~
#include <vector>
#include <iostream>
// UnionFind类,用于实现并查集算法
class UnionFind {
// 私有变量
private:
std::vector<int> parent; //成员变量,用于存储每个元素的父节点
std::vector<int> size; //成员变量,用于存储每个集合的大小,即集合中元素的数量
// 公共变量
public:
// 初始化并查集,参数 n 表示集合中元素的数量
UnionFind(int n) {
parent.resize(n);
size.resize(n, 1);
for (int i = 0; i < n; ++i) {
parent[i] = i;
}
}
// 查询集合的根,参数 x 表示要查询的元素
int find(int x) {
if (x != parent[x]) {
parent[x] = find(parent[x]);
}
return parent[x];
}
// 合并集合,参数 x 和 y 表示要合并的两个元素
void unite(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
if (size[rootX] < size[rootY]) {
parent[rootX] = rootY;
size[rootY] += size[rootX];
} else {
parent[rootY] = rootX;
size[rootX] += size[rootY];
}
}
}
// 查询是否为同一集合,参数 x 和 y 表示要查询的两个元素
void isConnected(int x, int y) {
if (find(x) == find(y)){
std::cout << x << "与" << y << "属于同一集合" << std::endl;
}else{
std::cout << x << "与" << y << "不属于同一集合" << std::endl;
}
}
};
int main() {
int n = 10;
UnionFind uf(n);
uf.unite(0, 6);
uf.unite(0, 7);
uf.unite(0, 8);
uf.unite(1, 4);
uf.unite(1, 9);
uf.unite(2, 3);
uf.unite(2, 5);
uf.isConnected(0, 6);
uf.isConnected(0, 9);
uf.unite(4, 8);
uf.unite(3, 9);
uf.isConnected(0, 5);
std::cout << "x = 4的根是:" << uf.find(4) << std::endl;
return 0;
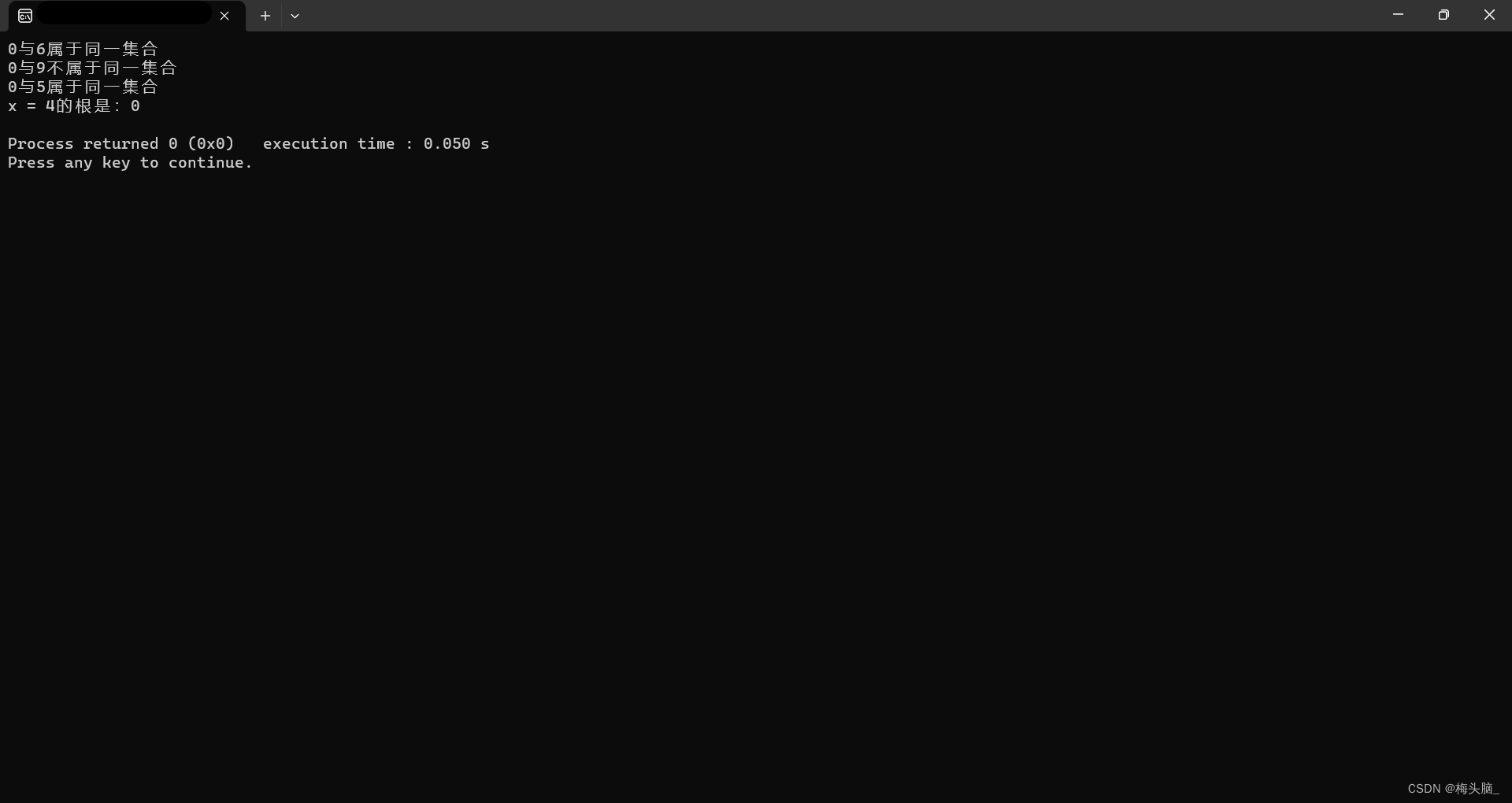
}🔯P1:执行结果
运行结果如下图所示~
🔚结语
博文到此结束,写得模糊或者有误之处,欢迎小伙伴留言讨论与批评,督促博主优化内容~😶🌫️😶🌫️博文若有帮助,欢迎小伙伴动动可爱的小手默默给个赞支持一下~🌟🌟