【国密】SM3密码杂凑算法（附源码分析）

news2025/10/31 8:44:16

一、前言

SM3 算法是中国国家密码管理局于 2010 年发布的一种密码杂凑算法，广泛地应用于数据的完整性校验、数字签名、消息认证码、密钥交换和数据加密等。密码杂凑算法需要满足三种基本属性：抗原像攻击、抗第二原像攻击、抗碰撞攻击，这三种基本属性分别对应三个问题：

  • 原像问题，已知哈希值 y y y 找出 x x x 使得 h ( x ) = y h(x)=y h(x)=y，其中 h ( ) h() h() 为哈希函数；
  • 第二原像问题，已知 x x x，找出 x ′ x^{\prime} x′ 满足 h ( x ) = h ( x ′ ) h(x) = h(x^{\prime}) h(x)=h(x′) ；
  • 碰撞问题，找出 x x x与 x ′ x^{\prime} x′ ，使其 h ( x ) = h ( x ′ ) h(x) = h(x^{\prime}) h(x)=h(x′) 。

SM3 算法采用了类似于 SHA-256 算法的 Merkle-Damgård 结构，并且使用了置换压缩和消息扩展算法，以提高算法的安全性和效率。SM3 算法的安全性已经得到了广泛认可，并且已被国际标准化组织 ISO/IEC 和国际电信联盟 ITU-T 接受为国际标准。

二、迭代哈希函数

迭代哈希函数是一种常见的密码杂凑函数，其基本思想是将输入数据分成固定长度的数据块，并对每个数据块进行迭代计算，最终输出一个固定长度的哈希值。迭代哈希函数的安全性和效率都比较高，因此在实际应用中得到了广泛的应用。

迭代哈希函数通常分为以下几个部分：

  • 消息填充，将输入数据按照一定规则进行填充，使其长度符合特定的要求。
  • 消息分组，将填充后的数据分成固定长度的数据块。
  • 压缩函数，对每个数据块进行压缩计算，得到一个中间状态值。
  • 消息扩展，根据中间状态值进行消息扩展，得到下一个数据块的输入。
  • 输出变换，将最后一个数据块的中间状态值进行处理，得到固定长度的哈希值。

[3] 给出压缩函数进行迭代压缩计算的示例：
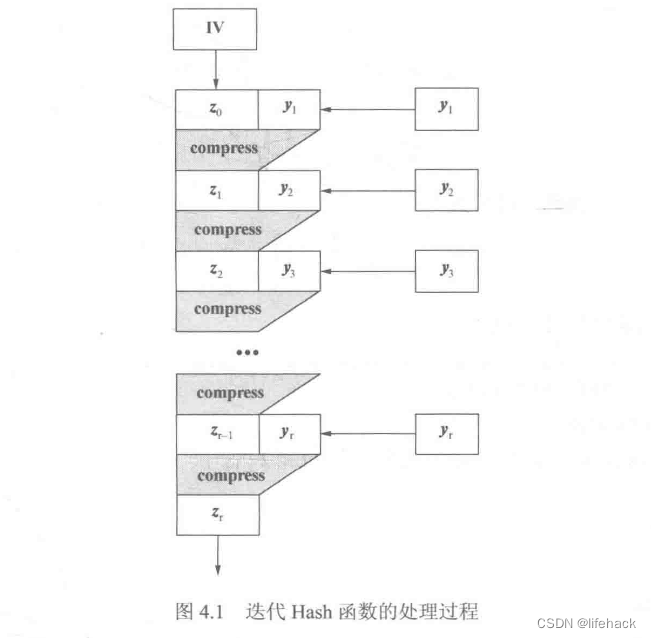
在这里插入图片描述
在这里插入图片描述
其中， z i z_i zi​ 为压缩计算的中间状态值， y i y_i yi​ 为消息分组后的数据块。

迭代哈希函数的安全性主要依赖于消息填充、压缩函数和消息扩展算法的设计。消息填充需要满足一定的安全性要求，以防止恶意攻击者对填充后的数据进行修改。压缩函数需要满足抗碰撞和抗原像性的要求，以保证哈希值的安全性。消息扩展算法需要满足一定的扩展性和安全性要求，以保证哈希函数的效率和安全性。迭代哈希函数的优点是输出长度固定，且能够处理任意长度的输入数据，具有高效性和安全性。常见的迭代哈希函数包括 MD5、SHA-1、SHA-2 和 SM3 等。在实际应用中，迭代哈希函数通常用于数字签名、消息认证码、密钥交换和数据加密等领域。

Merkle-Damgård 结构是一种常见的迭代哈希函数的实现方式，它将输入数据分成固定长度的数据块，并对每个数据块进行迭代计算，最终输出一个固定长度的哈希值。Merkle-Damgård 结构的主要特点是简单、高效、安全，因此在实际应用中得到了广泛的应用。Merkle-Damgård 结构主要由以下两个部分组成：

  • 压缩函数：对每个数据块进行压缩计算，得到一个中间状态值。
  • 消息扩展：根据中间状态值进行消息扩展，得到下一个数据块的输入。

Merkle-Damgård 结构将输入数据分成固定长度的数据块，然后对每个数据块调用压缩函数进行计算，得到一个中间状态值。中间状态值被用作消息扩展的输入，以生成下一个数据块的输入。迭代计算的过程一直持续到最后一个数据块处理完毕，然后将最后一个数据块的中间状态值进行处理，得到固定长度的哈希值。

Merkle-Damgård 结构的优点是简单、高效、安全，能够处理任意长度的输入数据，且输出长度固定。在实际应用中，Merkle-Damgård 结构通常用于实现 MD5、SHA-1、SHA-2 和 SM3 等常见的哈希函数。

三、SM3 算法

算法介绍

SM3 算法的设计目标是满足密码学的强度要求，具有高效性、安全性和灵活性。SM3 算法的输入为任意长度的消息，输出为一个 256 位的杂凑值。SM3 算法主要包括以下几个部分：

  • 消息填充，将消息进行填充，使其长度满足 512 位的倍数。
  • 消息分组，将填充后的消息分按512 比特进行分组。
  • 压缩函数，并对每个数据块进行压缩计算，得到中间状态值。
  • 消息扩展：根据中间状态值进行消息扩展，得到下一个数据块的输入。
  • 输出变换，将最后一个数据块的中间状态值进行处理，得到 256 比特的杂凑值。

在这里插入图片描述
在这里插入图片描述

SM3 密码杂凑算法特点：SM3 压缩函数整体结构与SHA-256 类似，但是增加了许多新的设计技术，包括：增加16步全异或操作，消息双字介入、增加快速雪崩效应的P置换等；能有效率地避免高概率的局部碰撞，有效地抵抗强碰撞性的差分分析、弱碰撞性的线性分析和比特追踪法等密码分析 [2]。

详细介绍与示例请参看SM3算法标准文档[1] 。

源码分析

GmSSL 库实现SM3 算法，相关源码分析如下：

// SM3 哈希长度，32字节=512比特
#define SM3_DIGEST_SIZE		32
// SM3 处理的消息分组为512比特，对应字节数为64
#define SM3_BLOCK_SIZE		64
#define SM3_STATE_WORDS		8
#define SM3_HMAC_SIZE		(SM3_DIGEST_SIZE)

/*
 * SM3 上下文信息
 */
typedef struct {
    // 字寄存器
	uint32_t digest[SM3_STATE_WORDS];
    // 已参与压缩函数计算数据块的长度（单位为数据块数）
	uint64_t nblocks;
    // 待参与压缩函数计算的数据块
	uint8_t block[SM3_BLOCK_SIZE];
    // 待参与压缩函数计算的数据块的长度（单位为字节）
	size_t num;
} SM3_CTX;


/**
 * 多个数据块迭代压缩，
 * @param digest 出参，压缩计算后字寄存器的状态值
 * @param data 入参，数据块
 * @param blocks 入参，数据块的数量
 */
void sm3_compress_blocks(uint32_t digest[8], const uint8_t *data, size_t blocks) {
    uint32_t A;
    uint32_t B;
    uint32_t C;
    uint32_t D;
    uint32_t E;
    uint32_t F;
    uint32_t G;
    uint32_t H;
    uint32_t W[68];
    uint32_t SS1, SS2, TT1, TT2;
    int j;

#ifdef SM3_SSE3

#endif

    while (blocks--) {

        A = digest[0];
        B = digest[1];
        C = digest[2];
        D = digest[3];
        E = digest[4];
        F = digest[5];
        G = digest[6];
        H = digest[7];


#ifdef SM3_SSE3

#else
        // 消息扩展，生成字 W_i，其中字W'_i 在此处并未计算，在压缩函数中计算
        for (j = 0; j < 16; j++)
            W[j] = GETU32(data + j * 4);

        for (; j < 68; j++)
            W[j] = P1(W[j - 16] ^ W[j - 9] ^ ROL32(W[j - 3], 15))
                   ^ ROL32(W[j - 13], 7) ^ W[j - 6];
#endif


        j = 0;

#define FULL_UNROLL
#ifdef FULL_UNROLL
        /*
         * 压缩函数 V^{i+1} = CF(V^{i}, B^{i})
         * 宏定义等价于下面两个for 循环
         */
        R8(A, B, C, D, E, F, G, H, 00);
        R8(A, B, C, D, E, F, G, H, 00);
        R8(A, B, C, D, E, F, G, H, 16);
        R8(A, B, C, D, E, F, G, H, 16);
        R8(A, B, C, D, E, F, G, H, 16);
        R8(A, B, C, D, E, F, G, H, 16);
        R8(A, B, C, D, E, F, G, H, 16);
        R8(A, B, C, D, E, F, G, H, 16);
#else

#endif

        digest[0] ^= A;
        digest[1] ^= B;
        digest[2] ^= C;
        digest[3] ^= D;
        digest[4] ^= E;
        digest[5] ^= F;
        digest[6] ^= G;
        digest[7] ^= H;

        data += 64;
    }
}

/*
 * 初始化上下文
 */
void sm3_init(SM3_CTX *ctx) {
    memset(ctx, 0, sizeof(*ctx));
    // 初始值IV
    ctx->digest[0] = 0x7380166F;
    ctx->digest[1] = 0x4914B2B9;
    ctx->digest[2] = 0x172442D7;
    ctx->digest[3] = 0xDA8A0600;
    ctx->digest[4] = 0xA96F30BC;
    ctx->digest[5] = 0x163138AA;
    ctx->digest[6] = 0xE38DEE4D;
    ctx->digest[7] = 0xB0FB0E4E;
}

/*
 * 将消息数据更新到上下文中
 */
void sm3_update(SM3_CTX *ctx, const uint8_t *data, size_t data_len) {
    size_t blocks;

    // 只保留低6位，通过按位与 0x3f=0b111111，限制ctx->num 在区间[0, 64]
    ctx->num &= 0x3f;
    if (ctx->num) {
        // 对于参与压缩函数计算的数据块，计算其凑齐64字节的剩余量 left
        size_t left = SM3_BLOCK_SIZE - ctx->num;
        // 输入数据块的长度小于 left，只拷贝，不参与压缩函数计算
        if (data_len < left) {
            memcpy(ctx->block + ctx->num, data, data_len);
            ctx->num += data_len;
            return;
        }
        // 输入数据块能凑齐64字节，计算1个分组下的压缩函数
        else {
            memcpy(ctx->block + ctx->num, data, left);
            sm3_compress_blocks(ctx->digest, ctx->block, 1);
            ctx->nblocks++;
            data += left;
            data_len -= left;
        }
    }

    // 针对剩下的输入数据块，计算压缩函数
    blocks = data_len / SM3_BLOCK_SIZE;
    if (blocks) {
        sm3_compress_blocks(ctx->digest, data, blocks);
        ctx->nblocks += blocks;
        data += SM3_BLOCK_SIZE * blocks;
        data_len -= SM3_BLOCK_SIZE * blocks;
    }

    // 剩余不足64字节输入数据块
    ctx->num = data_len;
    if (data_len) {
        memcpy(ctx->block, data, data_len);
    }
}

/*
 * 计算消息的哈希值
 */
void sm3_finish(SM3_CTX *ctx, uint8_t *digest) {
    int i;

    ctx->num &= 0x3f;
    // 将0x80 添加到消息末尾
    ctx->block[ctx->num] = 0x80;

    // 有余量添加64比特的消息长度l 二进制，直接添加k 个 0
    if (ctx->num <= SM3_BLOCK_SIZE - 9) {
        memset(ctx->block + ctx->num + 1, 0, SM3_BLOCK_SIZE - ctx->num - 9);
    }
    // 没有余量添加64比特的消息长度l 二进制，先补齐64个字节数据块，再补齐56个字节0，用于与消息长度l 构造下一个数据块
    else {
        memset(ctx->block + ctx->num + 1, 0, SM3_BLOCK_SIZE - ctx->num - 1);
        sm3_compress_blocks(ctx->digest, ctx->block, 1);
        memset(ctx->block, 0, SM3_BLOCK_SIZE - 8);
    }

    // 计算消息长度 l =(nblocks*2^9 + num*2^3) 二进制表示
    // block[56..59] = nblocks 的高9位
    PUTU32(ctx->block + 56, ctx->nblocks >> 23);
    // block[60..63] = nblocks 的低23位与num*2^3 之和
    PUTU32(ctx->block + 60, (ctx->nblocks << 9) + (ctx->num << 3));

    // 压缩函数计算最后一个数据分块
    sm3_compress_blocks(ctx->digest, ctx->block, 1);

    // 将字寄存器值转为256比特（32位 u8）杂凑值
    for (i = 0; i < 8; i++) {
        PUTU32(digest + i * 4, ctx->digest[i]);
    }
    memset(ctx, 0, sizeof(SM3_CTX));
}

/**
 * 计算SM3 哈希摘要
 * @param msg 入参，输入消息
 * @param msglen 入参，输入消息长度
 * @param dgst 出参，哈希摘要
 */
void sm3_digest(const uint8_t *msg, size_t msglen,
                uint8_t dgst[SM3_DIGEST_SIZE]) {
    SM3_CTX ctx;
    sm3_init(&ctx);
    sm3_update(&ctx, msg, msglen);
    sm3_finish(&ctx, dgst);
}

四、参考资料

[1] 国家密码管理局，SM3密码杂凑算法, 2010.
[2] 王小云,于红波.SM3密码杂凑算法[J].信息安全研究,2016,2(11):983-994.
[3] Douglas R. Stinson 著，冯登国 等译，密码学原理与实践（第三版），电子工业出版社，2016.

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/745562.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【动手学习深度学习--逐行代码解析合集】14多输入多输出通道

【动手学习深度学习--逐行代码解析合集】14多输入多输出通道

【动手学习深度学习】逐行代码解析合集 14多输入多输出通道 视频链接&#xff1a;动手学习深度学习–多输入多输出通道 课程主页&#xff1a;https://courses.d2l.ai/zh-v2/ 教材&#xff1a;https://zh-v2.d2l.ai/ 1、多输入通道 import torch from d2l import torch as d2l …
阅读更多...
[C语言][小游戏][猜拳游戏]

[C语言][小游戏][猜拳游戏]

C语言的奇妙旅行 一、模块化编程二、游戏基本设计2.1 确定计算机要出的手势2.2 显示“石头剪刀布”&#xff0c;然后玩家输入自己要出的手势2.3进行输赢判断&#xff0c;显示结果2.4询问是否继续2.5 基本程序 三、游戏实现的过程3.1将玩家的手势和电脑的手势显示出来 三、总代码…
阅读更多...
复习java基础

复习java基础

复习一天有点忘了的知识&#xff1a; 结构化编程 结构化程式设计(英语:Structured programming)是1960年代开始发展起来的一种编程典范。它采用子程序、程式码区块、for循环以及while循环等结构来取代传统的goto。 指导思想 自顶向下、逐步求精、模块化 编程过程 流程图是…
阅读更多...
CVPR 2023 | OVSeg: Open-Vocabulary Semantic Segmentation with Mask-adapted CLIP

CVPR 2023 | OVSeg: Open-Vocabulary Semantic Segmentation with Mask-adapted CLIP

CVPR 2023 | OVSeg: Open-Vocabulary Semantic Segmentation with Mask-adapted CLIP 论文&#xff1a;https://arxiv.org/abs/2210.04150代码&#xff1a;https://github.com/facebookresearch/ov-seg 架构设计 类别无关的 mask proposal generator&#xff1a;MaskFormer手动…
阅读更多...
linux端口被占用 关闭端口

linux端口被占用 关闭端口

1.查看端口是否被占用 netstat -anp |grep [端口号]2.查看占用的进程 lsof -i:[端口号]3.关闭进程 kill -9 [进程PID]LISTEN 表示被占用&#xff0c;3061/java 分别是&#xff1a;进程PID/进程 通过进程PID关闭进程
阅读更多...
桥接模式：解耦抽象与实现

桥接模式：解耦抽象与实现

桥接模式是一种结构型设计模式&#xff0c;它将抽象部分与实现部分分离&#xff0c;使它们可以独立地变化。本文将深入探讨桥接模式的原理、结构和使用方法&#xff0c;并通过详细的 Java 示例代码来说明。 1. 桥接模式的定义 桥接模式是一种将抽象部分与实现部分分离的设计模…
阅读更多...
数字信号处理复习知识点

数字信号处理复习知识点

目录 第一章&#xff1a;时域离散系统 1.什么是因果性和稳定性 2.模拟频率&#xff0c;模拟角频率&#xff0c; 数字频率之间的关系 3.什么是频谱混叠&#xff1f; 第二章&#xff1a;时域离散信号和系统的频域分析 1.时域离散信号傅立叶变换的定义 2.如何用模拟信号的傅立…
阅读更多...
电信青年员工踏上三千里数字化追梦之旅，数字员工为电信高质量发展注智赋能

电信青年员工踏上三千里数字化追梦之旅，数字员工为电信高质量发展注智赋能

导语&#xff1a; 近年来&#xff0c;广西电信紧紧围绕集团战略&#xff0c;聚焦产业数字化发展机遇&#xff0c;加强前瞻性技术研究和人工智能产业应用研究&#xff0c;为夯实高质量发展增添科技动力。 在数字中国建设的大背景下&#xff0c;广西电信全资子公司广西壮族自治区…
阅读更多...
推荐一款适合前端宝宝体质的数据库文档工具

推荐一款适合前端宝宝体质的数据库文档工具

先看效果 首页 安心食用 npx dbshowlatest按照提示输入相关信息 Welcome to the DB Show! v0.0.7? Use config from local? no ? Select a database type MySQL ? Enter the host name localhost ? Enter the port number 3306 ? Enter the user name root ? Ente…
阅读更多...
Linux slab 分配器源码解析

Linux slab 分配器源码解析

文章目录 前言一、slab分配器1.1 简介1.2 高速缓存描述符1.3 架构图 二、相关结构体2.1 struct array_cache2.2 struct kmem_list32.3 struct slab2.3.1 简介2.3.2 OFF_SLAB 三、创建和释放slab3.1 创建slab3.1.1 kmem_getpages3.1.2 alloc_slabmgmt3.1.3 slab_map_pages 3.2 释…
阅读更多...
常用数据分类算法原理介绍、优缺点分析与代码实现[LR/RF/DT/SVM/NavieBayes/GBDT/XGBoost/DNN/LightGBM等]

常用数据分类算法原理介绍、优缺点分析与代码实现[LR/RF/DT/SVM/NavieBayes/GBDT/XGBoost/DNN/LightGBM等]

本文的主要目的是总结记录日常学习工作中常用到的一些数据分类算法&#xff0c;对其原理简单总结记录&#xff0c;同时分析对应的优缺点&#xff0c;以后需要的时候可以直接翻看&#xff0c;避免每次都要查询浪费时间&#xff0c;欢迎补充。 机器学习领域中常用的分类模型包括以…
阅读更多...
分布式事物【Seata实现、下载启动Seata服务、搭建聚合父工程构建】(四)-全面详解（学习总结---从入门到深化）

分布式事物【Seata实现、下载启动Seata服务、搭建聚合父工程构建】(四)-全面详解（学习总结---从入门到深化）

目录 分布式事物解决方案_XA方案 分布式事物解决方案_Seata实现 Seata提供XA模式实现分布式事务_业务说明 Seata提供XA模式实现分布式事务_下载启动Seata服务 Seata提供XA模式实现分布式事务_搭建聚合父工程构建 创建工程distribute-transaction 字符编码 注解生效激活 Jav…
阅读更多...
three js模型旋转

three js模型旋转

如何让立方体模型旋转到指定的面 父页面 <b-modal ref"modal_mini" size"lg" centered static :hide-footer"true":dialog-class"[modal_mini]":content-class"position-static":body-class"p-0":header-class…
阅读更多...
上海亚商投顾：沪指放量调整 两市超4000只个股下跌

上海亚商投顾：沪指放量调整 两市超4000只个股下跌

上海亚商投顾前言&#xff1a;无惧大盘涨跌&#xff0c;解密龙虎榜资金&#xff0c;跟踪一线游资和机构资金动向&#xff0c;识别短期热点和强势个股。 市场情绪 沪指今日震荡调整&#xff0c;深成指、创业板指午后跌超1%。AI概念股集体下挫&#xff0c;CPO、算力等方向领跌&am…
阅读更多...
感知网络安全态势是什么？感知网络安全态势如何实施

感知网络安全态势是什么？感知网络安全态势如何实施

网络安全是当今社会中一个非常重要的话题。随着互联网的普及和信息技术的发展&#xff0c;网络安全问题日益突出。为了有效应对各种网络威胁和攻击&#xff0c;网络安全态势感知成为了一种关键的技术手段。 网络安全态势感知的定义 网络安全态势感知是指通过对网络环境中的各种…
阅读更多...
2023-07-11力扣每日一题

2023-07-11力扣每日一题

链接&#xff1a; https://leetcode.cn/problems/maximum-alternating-subsequence-sum/ 题意&#xff1a; 给定一个数组&#xff0c;求一个子序列&#xff0c;使这个子序列的奇数位和-偶数位和最大&#xff08;下标从1开始的话|反正第一个数是&#xff09; 解&#xff1a;…
阅读更多...
基于linux下的高并发服务器开发（第一章）-Linux环境开发搭建1.1

基于linux下的高并发服务器开发（第一章）-Linux环境开发搭建1.1

1、安装虚拟机 2、在虚拟机中安装Linux系统 &#xff08;1&#xff09;新建虚拟机向导 点击虚拟机设置&#xff0c;使用ISO映像文件(M) &#xff08;2&#xff09;Ubuntu18安装 点击现在安装 点击继续 静静地接下来的安装即可 安装好后&#xff0c;安装VMware Tools 将压缩…
阅读更多...
设计原则及设计模式基础

设计原则及设计模式基础

设计模式是一套被反复使用的、多数人知晓的、经过分类编目的代码设计经验的总结&#xff0c;使用设计模式是为了可以重用代码&#xff0c;让代码更容易被他人理解并且提高代码的可靠性。 1 设计模式概述 GoF(Gang Of Four 四人组&#xff0c;指4位著名软件工程学者)&#xff…
阅读更多...
ubuntu安装单个redis服务

ubuntu安装单个redis服务

1.apt-get install redis-server 使用lighthouse用户这样操作会报与权限有关的错误&#xff0c; 改成使用root账号操作 2.安装完成后&#xff0c;Redis服务器会自动启动&#xff0c;查看进程是否正常启动 ps -axu|grep redis redis 18689 0.1 0.4 40136 6860 ? …
阅读更多...
第3讲 Camera Sensor 数据流

第3讲 Camera Sensor 数据流

Camera Sensor Block Camera Sensor Output Format raw8 一个像素点用8bit来表示&#xff0c;范围0&#xff5e;256 raw10 一个像素点用10bit来表示&#xff0c;范围0&#xff5e;1024 raw12 一个像素点用12bit来表示&#xff0c;范围0&#xff5e;4096 Camera Sensor Fr…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023