博客中所有内容均来源于自己学习过程中积累的经验以及对yalmip官方文档的翻译:YALMIP
1.Yalmip工具箱的下载与安装
1.1下载
Yalmip的作者是Johan Löfberg,是由Matlab平台编程实现的一个免费开源数学优化工具箱,在官网上就可以下载。官方下载链接如下:
Download - YALMIP
下载时可以选择最新版本或者旧版本(如果使用的Matlab版本比较旧,有可能与最新版Yalmip工具箱不兼容,这时候就可以选择下载旧版本的Yalmip)
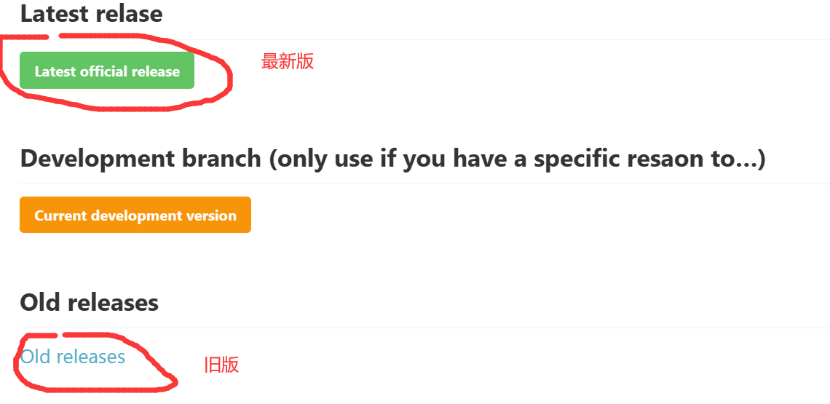
图1 Yalmip工具箱下载
1.2安装
Yamlip工具箱所有功能都是基于m文件实现的,因此安装过程实际上就是把Yalmip工具箱的路径添加到Matlab平台中,具体安装方式有以下几种:
1)手动添加路径
第一步,将下载的压缩包解压,然后把解压后的文件夹放在Matlab路径中的toolbox中(也可以随便放在其他的文件夹中,只要保证该文件夹不会被删除,被移动即可)。

第二步,将Yalmip工具箱添加到Matlab的路径中。

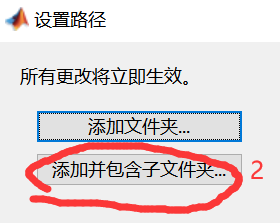
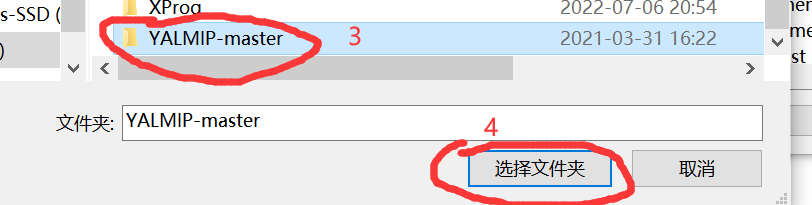
 图2 Matlab手动添加路径示意
图2 Matlab手动添加路径示意
2)使用addpath(genpath(pwd))命令
pwd表示当前路径,这个命令表示将当前文件夹下的所有子文件夹都添加到Matlab的路径中。首先使用时首先将下载的压缩包解压,然后把解压后的文件夹放在Matlab路径中的toolbox中(也可以随便放在其他的文件夹中,只要保证该文件夹不会被删除,被移动即可)。然后使用addpath(genpath(pwd))命令,并将其中的pwd修改为对应的路径即可,例如:
addpath(genpath(‘D:\Program Files\MATLAB\R2016b\toolbox\YALMIP-master’))1.3测试
安装成功后,可以使用yalmiptest函数测试是否安装成功。使用时在命令行输入yalmiptest并回车,Yalmip会自动求解一组优化问题来测试工具箱是否安装成功(中间有一段需要输入任意内容并回车,才能继续测试):
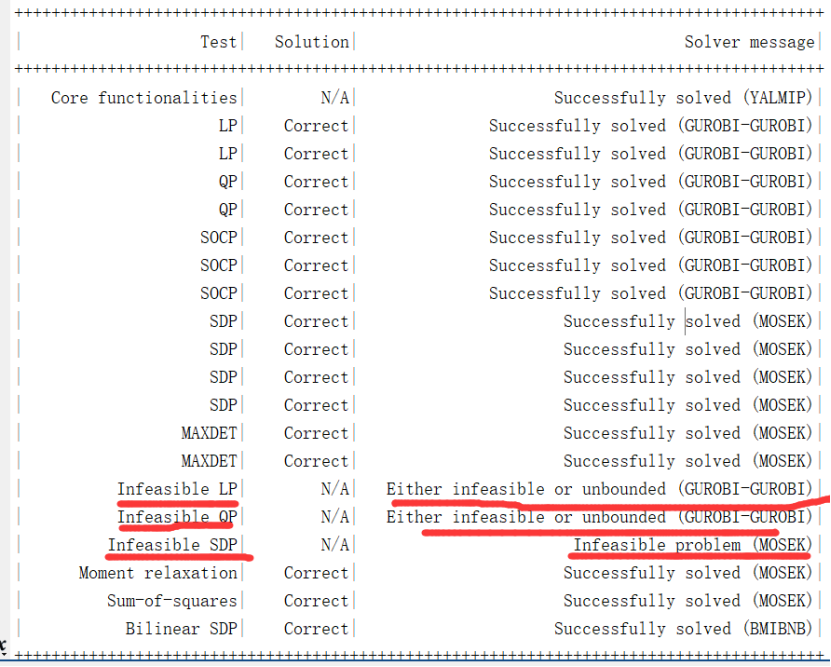
图3 Yalmip测试结果
如果和图3的求解结果一样,除了三个无解的问题,都显示”successfully solved”,表示工具箱可以正常使用了。但是,在求解优化问题时,Yalmip其实相当于“中间商”的地位,只是将各类求解器不同的数学建模方式修改为统一的形式,真正求解优化问题的还是那些求解器。工具箱中已经内置了一些免费的求解器,可以求解简单的优化问题,但针对复杂问题这些求解器的性能可能不是很好,这时候就需要功能更强大的商业求解器了。具有学术免费版的商业求解器主要有Gurobi、Cplex、Mosek,它们的下载地址和优缺点如表1所示:
表1 常用的学术免费版商业求解器
| 求解器 | 官网地址 | 优点 | 缺点 |
| Gurobi | http://www.gurobi.com | 1.集成了启发式算法 2.MILP求解性能排名前列 3.有官方中文网站,学术许可证申请容易 4.学术版没有规模限制 | 1.学术许可证只有一年有效,到期需要重新申请 2.使用人数较少,遇到问题时通过检索不容易找到答案 |
| Cplex | IBM Products | 1.拥有自己的建模环境 Ilog,也支持Java、C++、C 等语言 2.目前使用人数最多,通过检索较容易找到相关问题的解答 | 免费版和学术版都有规模限制,无法求解大规模问题 |
| Mosek | http://www.mosek.com | 内点法性能比较好,解SOCP、SDP等锥优化性能最优。 | 学术许可申请比较麻烦,需要学校邮箱支持 |
2.Yalmip使用方法介绍
使用Yalmip工具箱包括定义变量、定义约束条件、定义目标函数、定义求解器选项、求解优化问题以及检查优化结果并获取优化问题的解。下面的代码是Yalmip官方给出的示例,包括了上述所有步骤(PS:下文代码选择的求解器为cplex,如果没有安装cplex,只需在定义options时删除该求解器的设置,Yalmip将自动选择其他已安装的求解器):
% 定义变量
x = sdpvar(10,1);
% 设置约束条件
Constraints = [sum(x) <= 10, x(1) == 0, 0.5 <= x(2) <= 1.5];
for i = 1 : 7
Constraints = [Constraints, x(i) + x(i+1) <= x(i+2) + x(i+3)];
end
% 定义目标函数
Objective = x'*x + norm(x,1);
% 使用options结构体来为YALMIP和所需求解器指定优化参数
options = sdpsettings('verbose',1,'solver','cplexg');
% 将约束条件、目标函数和选项作为输入传递给优化函数,进行问题求解
sol = optimize(Constraints,Objective,options);
% 获取最终解或进行错误分析
if sol.problem == 0
% 获取解的值
disp(‘求解成功’)
solution = value(x);
else
disp('出错了!');
sol.info
yalmiperror(sol.problem)
end下面将对以上步骤分别进行介绍。
2.1定义决策变量
工具箱中定义决策变量的命令包括Binvar,blkvar,intvar,sdpvar和semivar,这里仅介绍sdpvar的用法,其余命令和sdpvar的用法相似。
sdpvar用于定义连续型的决策变量,其基本语法如下:
x = sdpvar(n)
x = sdpvar(n,m)
x = sdpvar(n,m,'type')
x = sdpvar(n,m,'type','field')
x = sdpvar(dim1,dim2,dim3,...,dimn,'type','field')
sdpvar x例如定义一个n行m列决策变量P的方法如下:
P = sdpvar(n,m);需要注意的是,使用sdpvar定义决策变量时,若决策变量为方阵,则默认其为对称阵(如果使用sdpvar定义了方阵x,则x(i,j) = x(j,i))。
例如,定义一个3行3列决策变量P的语法如下:
P = sdpvar(3,3);这时候变量P默认为一个对称矩阵,也就是P(1,2) = P(2,1),P(1,3) = P(3,1),P(2,3) = P(3,2)。如果需要定义一个不对称的变量P,则需要添加’full’,语法如下:
P = sdpvar(3,3,’full’);定义矩阵时没有添加参数’full’,导致变量默认为方阵,这是初学Yalmip工具箱最容易犯一个错误,需要留意!!!!我们很多时候定义变量时,维度都是不确定的,为了避免出错,就可以在不需要定义对称矩阵时,都添加参数’full’。
另外一点需要说明的是,Matlab中对于标量和矩阵的绝大部分函数都可以用于sdpvar类型变量,记住这一点可以简化很多代码量。
例如:
x = sdpvar(1,6);
len_x = length(x)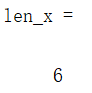
对于sdpvar类型变量,建模时其他常用的命令还有diag、eye、end等等,这就需要在使用过程中慢慢地尝试。定义决策变量的更多内容将在后文进行介绍。
2.2定义约束条件
Yalmip工具箱中可以非常方便的定义约束条件,针对决策变量使用约束条件定义函数或约束条件定义运算符即可表示一个约束条件。最常用的约束条件定义运算符包括’>=’、’<=’、’==’,分别表示大于等于、小于等于和等于。
例如,假设二维决策变量x的约束条件包括:
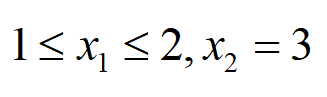
上面的式子实际上包含三个约束条件,可以分别写成:
x = sdpvar(1,2);
C1 = [x(1) >= 1];
C2 = [x(1) <= 2];
C3 = [x(2) == 3];将每个约束条件通过矩阵拼接或者使用’+’相加的方式连接在一起,便可以组合多个约束条件。
C = [C1 , C2 , C3];或者
C_dot = C1 + C2 + C3;两种表达方式是完全等价的。上面的例子中,变量x1的约束是一个连续不等式,也可以同时进行定义,方式如下:
C4 = [1 <= x(1) <= 2];需要注意的是,Yalmip中不支持严格的不等式约束(也就是不含等号的不等式),如果使用了严格的不等号,将会收到非常经典的Yalmip“猫猫警告”,例如,运行下面这份代码,将会弹出如图4的警告:
x = sdpvar(1,2);
C1 = [x(1) > 1];
图4 严格不等号收到的错误提示
除了最常用的约束条件定义运算符包括’>=’、’<=’、’==’之外,Yalmip中还支持使用其他命令定义约束,如alldifferent, binary, complements, cone, cut, expcone, iff, implies, integer, ismember等等,将在后文进行详细介绍。
2.3定义目标函数
Yalmip优化时默认的目标函数是取最小值。如果目标函数是取最大值,在目标函数前加上一个负号就可以了。
例如,有两个不同的目标函数分别为:
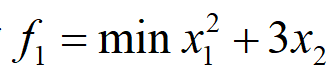
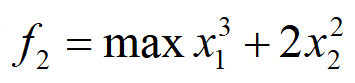
定义这两个目标函数的代码如下:
x = sdpvar(1,2);
f1 = x(1)^2 + 3*x(2);
f2 = -(x(1)^3 + 2*x(2)^2);2.4设置求解参数
使用sdpsettings函数可以对求解的相关参数进行设置。最常用的设置选项包括求解器的选择(solver)、命令行结果展示的详细程度(verbose)与步骤展示(showprogress)。例如,下面的代码就是将求解器选择为cplex,结果展示的详细程度为0(最少的命令行展示,最大值为3),不显示步骤(showprogress为0):
ops = sdpsettings('solver','cplex','verbose',0,'showprogress',0);也可以先对选项结构体进行赋值,然后通过结构体操作修改具体选项的内容,例如:
ops = sdpsettings;
ops.solver = cplex;
ops.verbose = 0;
ops.showprogress = 0;Yalmip求解的参数非常多,如果想要查看完整的参数,可以先定义一个默认的参数选项ops,然后在工作区或者命令行查看该结构体的内容:
>> ops
ops =
包含以下字段的 struct:
solver: ''
verbose: 1
debug: 0
usex0: 0
warning: 1
cachesolvers: 0
showprogress: 0
saveduals: 1
removeequalities: 0
savesolveroutput: 0
savesolverinput: 0
saveyalmipmodel: 0
convertconvexquad: 1
assertgpnonnegativity: 1
thisisnotagp: 0
radius: Inf
relax: 0
dualize: 0
savedebug: 0
expand: 1
allowmilp: 1
allownonconvex: 1
shift: 0
dimacs: 0
beeponproblem: [-5 -4 -3 -2 -1]
mosektaskfile: ''
bisection: [1×1 struct]
bilevel: [1×1 struct]
bmibnb: [1×1 struct]
bnb: [1×1 struct]
cutsdp: [1×1 struct]
kkt: [1×1 struct]
moment: [1×1 struct]
mp: [1×1 struct]
mpcvx: [1×1 struct]
plot: [1×1 struct]
robust: [1×1 struct]
sos: [1×1 struct]
refiner: [1×1 struct]
baron: []
bintprog: [1×1 struct]
bonmin: []
cdcs: [1×1 struct]
cdd: [1×1 struct]
cbc: [1×1 struct]
clp: [1×1 struct]
cplex: [1×1 struct]
coneprog: []
csdp: [1×1 struct]
dsdp: [1×1 struct]
ecos: []
filtersd: [1×1 struct]
fmincon: [1×1 struct]
fminsearch: [1×1 struct]
frlib: [1×1 struct]
glpk: [1×1 struct]
gurobi: [1×1 struct]
ipopt: [1×1 struct]
intlinprog: [1×1 optim.options.Intlinprog]
knitro: [1×1 struct]
linprog: [1×1 struct]
lmilab: [1×1 struct]
lmirank: [1×1 struct]
logdetppa: [1×1 struct]
lpsolve: [1×1 struct]
lsqnonneg: [1×1 struct]
lsqlin: [1×1 struct]
kypd: [1×1 struct]
kktqp: [1×1 struct]
nag: [1×1 struct]
mosek: [1×1 struct]
nomad: []
ooqp: []
penbmi: [1×1 struct]
penlab: []
pensdp: [1×1 struct]
pop: [1×1 struct]
qpoases: []
osqp: []
qsopt: [1×1 struct]
quadprog: [1×1 struct]
quadprogbb: [1×1 struct]
scip: [1×1 struct]
scs: [1×1 struct]
sdpa: [1×1 struct]
sdplr: [1×1 struct]
sdpt3: [1×1 struct]
sdpnal: [1×1 struct]
sedumi: [1×1 struct]
sparsepop: [1×1 struct]
snopt: [1×1 struct]
sparsecolo: [1×1 struct]
vsdp: [1×1 struct]
xpress: []
default: [1×1 struct]求解参数设置的更多内容将在后文进行介绍,此处不再赘述。
2.5求解优化问题
Yalmip中求解优化问题用到的函数为optimize,使用的语法为:
sol = optimize(Constraints,Objective,options);其中,Constraints表示约束条件,Objective表示目标函数,options表示求解的参数。
如果只需要在约束条件中找到决策变量的一组解,就可以省略目标函数,例如:
x = sdpvar(1,2);
Constraints = [x <= 3 , x(1) >= 2 , x(2) >= 1];
ops = sdpsettings;
sol = optimize(Constraints);或者将最后一行代码改为:
sol = optimize(Constraints , [] , ops);就可以在省略目标函数的同时,使用自己定义的求解参数。想要求解完整的优化问题,在加上目标函数即可:
x = sdpvar(2,1);
Constraints = [x <= 3 , x(1) >= 2 , x(2) >= 1];
Objective = [1 3]*x;
ops = sdpsettings;
sol = optimize(Constraints , Objective , ops);上面2.3节提到,因为Yalmip默认是求目标函数最小值,所以求最大值时可以在目标函数前加一个负号。当然,也可以在定义目标函数时保持原有的形式,使用optimize求解时给目标函数添加负号,可实现一样的效果。
sol = optimize(Constraints , Objective , ops);2.6检查并获取优化问题的解
optimize函数的返回值sol是一个包含六个字段的结构体:
>> sol
sol =
包含以下字段的 struct:
yalmipversion: '20210331'
matlabversion: '9.1.0.441655 (R2016b)'
yalmiptime: 0.0851
solvertime: 0.0439
info: 'Successfully solved (GUROBI-GUROBI)'
problem: 0其中,yalmipversion表示Yalmip工具箱的版本,matlabversion表示Matlab的版本,yalmiptime表示Yalmip的建模时间,solvertime表示求解器的求解时间,info表示返回的信息,problem为求解成功的标志,0表示求解成功,1表示求解失败。
其中最重要的参数就是problem和info,可以显示求解是否成功,以及可能遇到的问题。因此通常可以在optimize函数求解之后再加一部分代码来展示是否求解成功和求解失败的原因:
if sol.problem == 0
disp('求解成功')
else
disp('求解失败,失败原因为:')
disp(sol.info)
end以下的代码是一个能求解成功的例子:
x = sdpvar(2,1);
Constraints = [x <= 3 , x(1) >= 2 , x(2) >= 1];
Objective = [1 3]*x;
ops = sdpsettings;
sol = optimize(Constraints , Objective , ops);
if sol.problem == 0
disp('求解成功')
else disp('求解失败,失败原因为:')
disp(sol.info)
end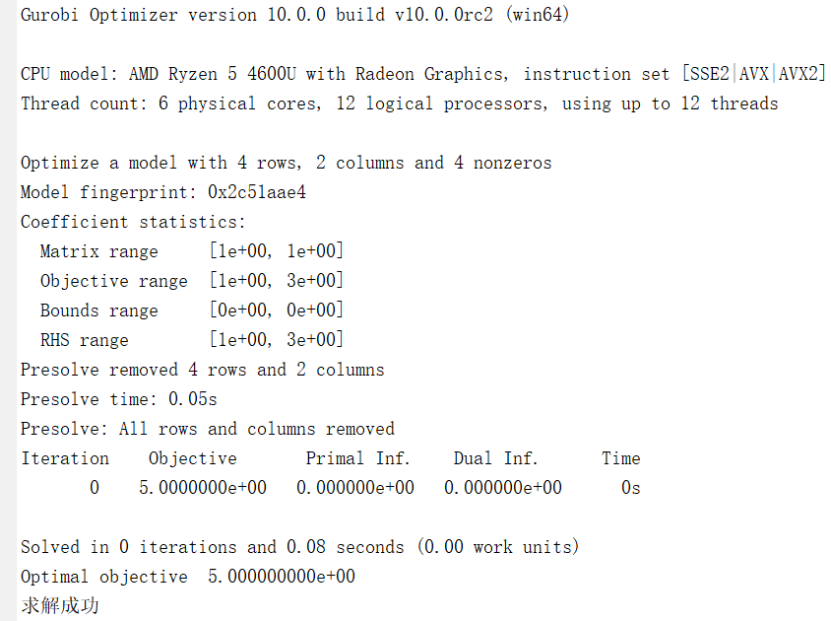
下面的例子是一个求解失败的代码:
x = sdpvar(2,1);
Constraints = [x <= 1 , x(1) >= 2 , x(2) >= 1];
Objective = [1 3]*x;
ops = sdpsettings;
sol = optimize(Constraints , Objective , ops);
if sol.problem == 0
disp('求解成功')
else
disp('求解失败,失败原因为:')
disp(sol.info)
end
因为约束条件中x1≤1且x1≥2,所以导致优化问题无解。
在确保优化问题求解成功的情况下,可以采用value命令或者目标函数或者决策变量的取值,例如:
x = sdpvar(2,1);
Constraints = [x <= 3 , x(1) >= 2 , x(2) >= 1];
Objective = [1 3]*x;
ops = sdpsettings;
sol = optimize(Constraints , Objective , ops);
if sol.problem == 0
disp('求解成功')
x1 = value(x(1))
x2 = value(x(2))
Objective = value(Objective)
else
disp('求解失败,失败原因为:')
disp(sol.info)
end结果为:
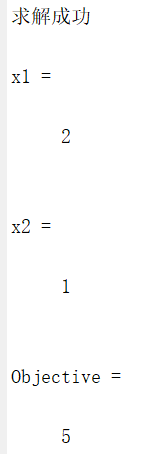
表示这个优化问题的最优解为x1=2,x2=1,目标函数最小值为5。
3.测试题
3.1测试1
求如下优化问题的解
max z=3x1+x2
s.t. x1-x2≥-2
x1-2x2≤3
3x1+2x2≤14
x1≥0, x2≥0
3.2测试2
找出下列代码中的错误并修改,使优化问题可以正常求解:
clc
clear
x = sdpvar(2,2);
Constraints = [x >= 1 , 5 >= x(1,:) >= 3 , 8 >= x(2,:) >= 6];
Objective = sum(x(:));
ops = sdpsettings('solver' , 'BNB' , 'verbose' , 3 , 'showprogress' , 1);
sol = optimize(Constraints , Objective , ops);
if sol.problem == 0
disp('求解成功')
else
disp('求解失败,失败原因为:')
disp(sol.info)
end3.3测试3
某厂生产甲乙两种口味的饮料,每吨甲饮料需用原料6千克,工人10名,可获利10万元。每吨乙饮料需用原料5千克,工人20名,可获利9万元。今工厂共有原料60千克,工人150名,又由于其他条件所限甲饮料产量不超过8吨。问如何安排生产计划,即两种饮料各生产多少使获利最大?使用Matlab+Yalmip工具箱求解上述问题。
3.4测试题参考答案
第一章测试题的参考答案可以从下面的链接中获取:
https://download.csdn.net/download/weixin_44209907/88035061