运动控制--双S型 + PID
- 1 介绍
- 1.1 概述
- 1.2 梯形速度曲线 VS 双S型速度曲线
- 2 运动控制器
- 2.1 运动控制器的构成
- 2.2 轨迹生成器
- 2.3 插补器
- 2.4 控制回路
- 3 PID
- 4 双 S 型
- 4.1 介绍
- 4.2 双S模型(7段S型)
- 规划参数
- 算法公式
- 轨迹分类
- 5 多种速度规划对比 【引用 Marc Pony】
- 6 示例
- 基于PID控制策略的机械臂轨迹跟踪控制
- Kinematically Constrained Jerk–Continuous S-Curve Trajectory Planning in Joint Space for Industrial Robots
- Time-Optimal Asymmetric S-Curve Trajectory Planning of Redundant Manipulators under Kinematic Constraints
- 参考
1 介绍
1.1 概述
实现单电机的双 S 型轨迹规划,加上PID控制。
理想状态下,双S型完全可以平滑的控制速度达到自己的期望。实际运算和控制时,周期不稳定,响应不及时等,会造成偏差,这个时候就需要PID来控制,进一步保证运动平滑。
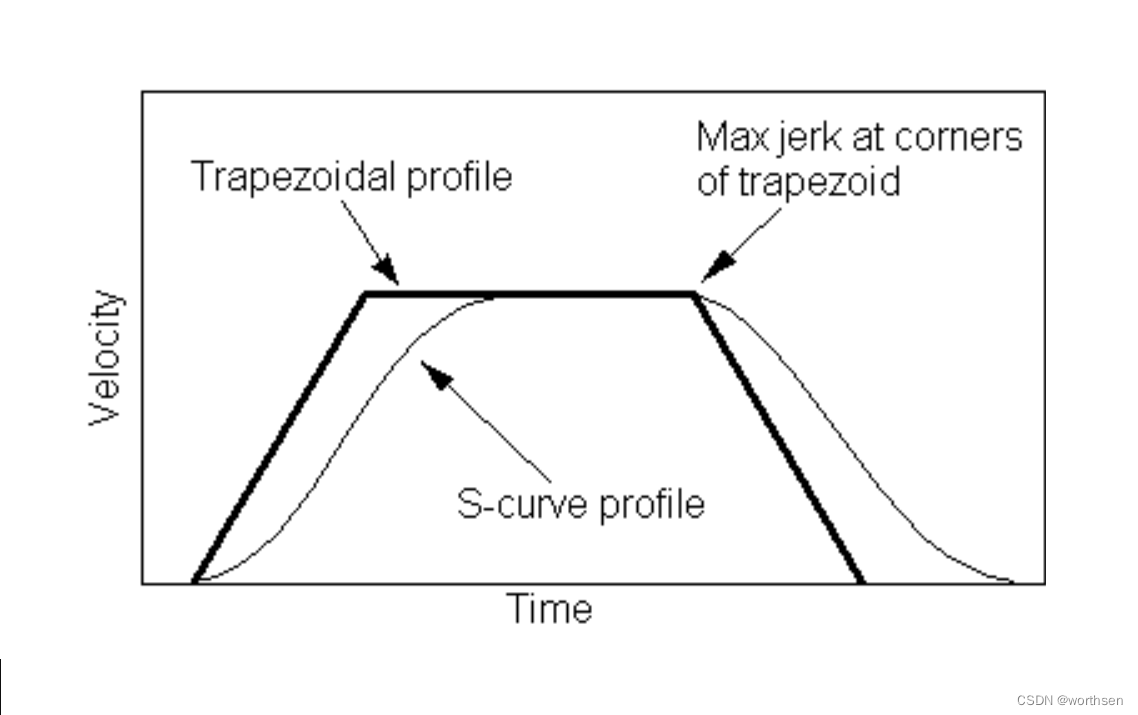
1.2 梯形速度曲线 VS 双S型速度曲线
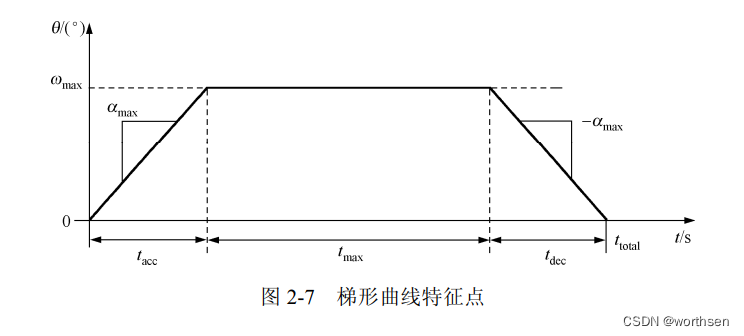
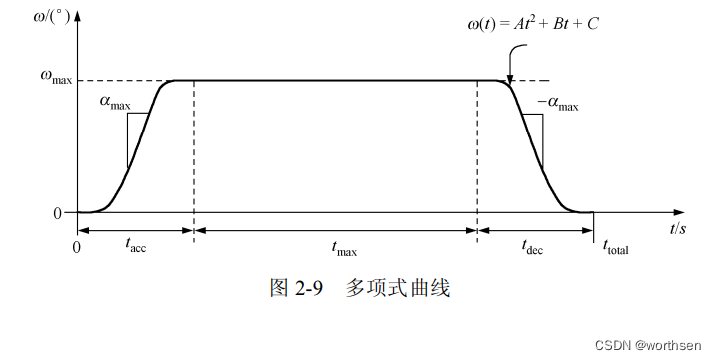
梯形速度规划的加速度曲线是不连续的,这对于系统是有害的。从机械系统的角度来说,不连续的加速度会产生不必要的冲击力,使得机械系统产生抖动甚至破坏。双S型速度规划采用两段线性区间组合的方法解决加速度不连续的问题,线性段端点处采用抛物线过渡的方法,保证连接处的加速度曲线连续。
2 运动控制器
2.1 运动控制器的构成
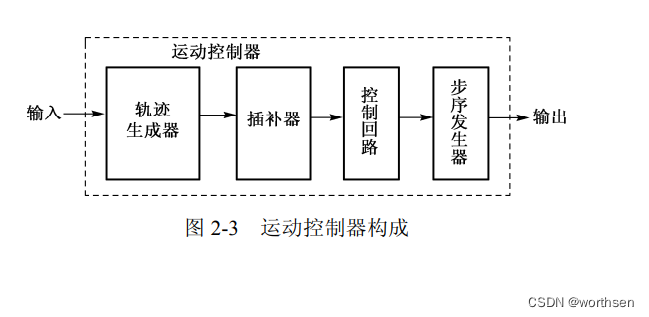
运动控制器由轨迹生成器、插补器、控制回路和步序发生器四部分构成,如图 2-3 所示。其基本原理为:运动控制器根据任务的需要,首先由轨迹生成器计算出任务希望的理想轨迹,插补器根据位置或者速度反馈单元的实际状态,按照轨迹生成器的要求,计算出驱动单元下一步将要执行的命令,然后交由控制回路进行精确控制。如果是步进电机,则还有一部分就是步序发生器,步序发生器根据控制回路控制指令进一步生成控制相序和脉冲,达到控制运动对象的目的。
2.2 轨迹生成器
轨迹生成器的主要作用就是根据运动任务要求,为系统生成运动轨迹,作为运动系统控制器插补器的输入设定。轨迹生成器的职责是把运动控制器的输入转化为系统希望得到的理想轨迹。运动轨迹是运动系统必须要完成的运动任务。就运动控制器而言,轨迹生成器是运动控制器三个核心部件之一,轨迹生成器性能好与坏对运动控制器起着至关重要的作用。我们这里所说的轨迹是广义上的轨迹,广义上的轨迹可以是路径或者轮廓轨迹,也可以是速度轨迹,还可以是加速度轨迹。狭义上的轨迹则特指路径或者轮廓轨迹。
如下是单轴点对点运动轨迹:
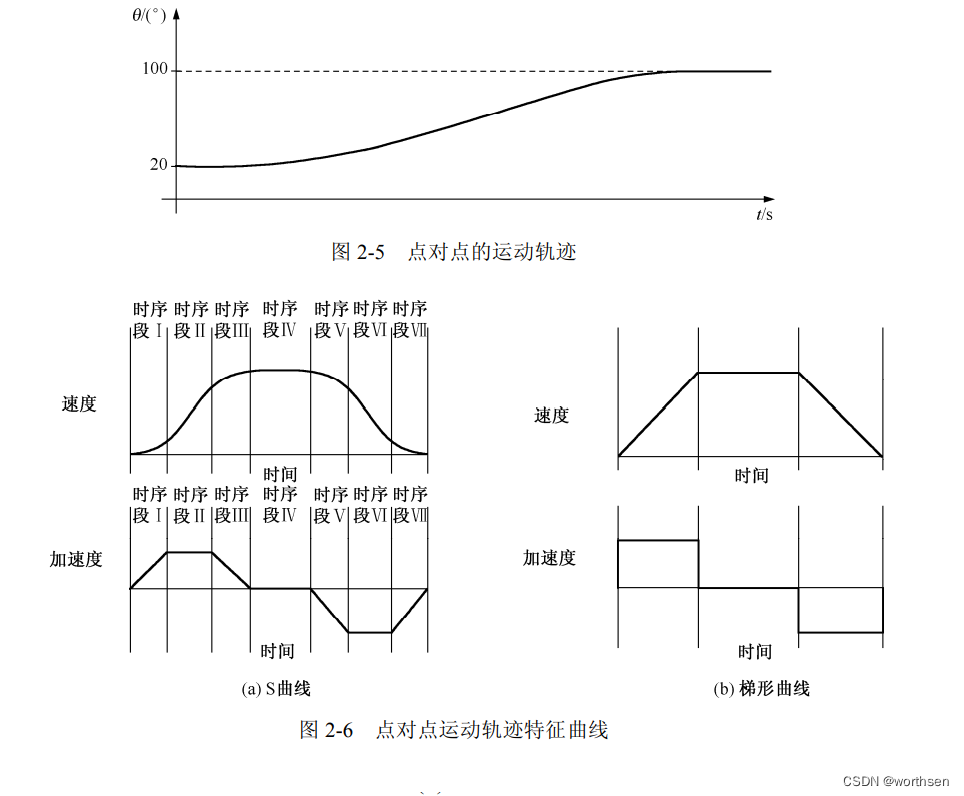
2.3 插补器
插补器是运动控制器中的算法。所谓“插补”,就是在一条已知起点和终点的曲线上进行数据点的密化。通常,可以采用的形式有简单的一次插补、二次插补或者更为复杂一些的三次样条函数插补。插补结果将送入控制回路。
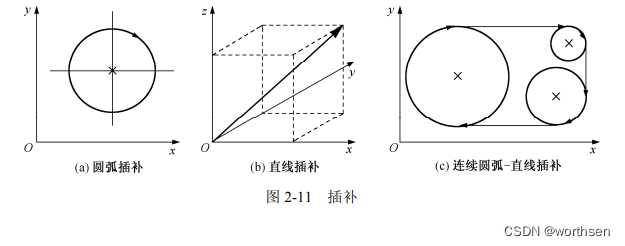
按照数学模型,可分为一次(直线插补)、二次(圆弧插补、抛物线插补、椭圆、双曲线、二次样条曲线)和高次(样条线插补)。
目前,应用最多的插补分为两类:基准脉冲插补和数据采样插补。
2.4 控制回路
在运动控制器中固化有控制算法,由算法依据期望的位置或速度与实际的位置或速度的差值信号进行计算。运动控制器通常使用增强型 PID(比例、积分、微分)算法,使得控制功能更加强大。PID 的增益设定值决定控制回路的控制能力。
3 PID


e
(
t
)
=
K
p
e
(
t
)
+
K
i
∫
0
t
e
(
t
)
d
t
+
K
d
d
e
(
t
)
d
t
t
≈
k
τ
(
k
=
0
,
1
,
2
,
.
.
.
)
u
(
t
)
≈
u
(
k
)
e
(
t
)
≈
e
(
k
)
∫
0
t
e
(
τ
)
d
τ
≈
τ
∑
j
=
0
k
e
(
j
τ
)
=
τ
∑
j
=
0
k
e
j
d
e
(
t
)
d
t
≈
e
(
k
τ
)
−
e
(
(
k
−
1
)
τ
)
τ
=
e
k
−
e
k
−
1
τ
u
(
k
)
=
K
p
e
(
k
)
+
K
i
τ
∑
j
=
0
k
e
(
j
)
+
K
d
e
(
k
)
−
e
(
k
−
1
)
τ
u
(
k
−
1
)
=
K
p
e
(
k
−
1
)
+
K
i
τ
∑
j
=
0
k
−
1
e
(
j
)
+
K
d
e
(
k
−
1
)
−
e
(
k
−
2
)
τ
K
i
=
K
p
T
i
K
d
=
K
p
T
d
K
I
=
K
p
∗
τ
T
i
=
K
i
τ
K
D
=
K
p
T
d
τ
=
K
D
τ
Δ
u
k
=
u
(
k
)
−
u
(
k
−
1
)
=
K
p
(
e
(
k
)
−
e
(
k
−
1
)
+
τ
T
i
e
(
k
)
+
T
d
e
(
k
)
−
2
e
(
k
−
1
)
+
e
(
k
−
2
)
τ
)
=
K
p
(
1
+
τ
T
i
+
T
d
τ
)
e
(
k
)
−
K
p
(
1
+
2
T
d
τ
)
e
(
k
−
1
)
+
K
p
T
d
τ
e
(
k
−
2
)
=
A
e
(
k
)
+
B
e
(
k
−
1
)
+
C
e
(
k
−
2
)
\begin{align} e(t) & = K_pe(t) + K_i\int_{0}^{t}e(t)dt + K_d\frac{de(t)}{dt} \tag{1-1} \\ \notag \\ t & ≈ k \tau (k=0,1,2,...) \notag\\ u(t) & ≈ u(k) \notag \\ e(t) & ≈ e(k) \notag \\ \int_{0}^{t}e(τ)dτ & ≈ \tau \sum_{j=0}^k e(j \tau) = \tau \sum_{j=0}^k e_j \tag{1-2} \\ \dfrac{de(t)}{dt} & ≈ \dfrac{e(k\tau)-e((k-1)\tau)}{\tau} = \dfrac{e_k-e_{k-1}}{\tau} \notag \\ \notag \\ u(k) & =K_pe(k)+K_i \tau \sum_{j=0}^{k}e(j) + K_d \dfrac{e(k)-e(k-1)}{\tau} \tag{1-3} \\ u(k-1) & = K_pe(k-1)+K_i \tau \sum_{j=0}^{k-1}e(j) + K_d \dfrac{e(k-1)-e(k-2)}{\tau} \tag{1-4} \\ \notag \\ K_i & = \dfrac{K_p}{T_i} \notag\\ K_d & = K_pT_d \notag\\ K_I & = \dfrac{K_p*\tau}{T_i} = K_i \tau \tag{1-5} \\ K_D & = K_p\dfrac{T_d}{\tau} = \dfrac{K_D}{\tau} \notag\\ \notag \\ \Delta u_k = u(k) - u(k-1) & = K_p \Bigl(e(k)-e(k-1)+ \dfrac{\tau}{T_i} e(k) + T_d \dfrac{e(k)-2e(k-1)+e(k-2)}{\tau} \Bigl) \notag \\ & = K_p(1+\dfrac{\tau}{T_i}+\dfrac{T_d}{\tau})e(k) - K_p(1+\dfrac{2T_d}{\tau})e(k-1)+K_p\dfrac{T_d}{\tau}e(k-2) \tag{1-6} \\ & = Ae(k) + Be(k-1) + Ce(k-2) \notag \end{align}
e(t)tu(t)e(t)∫0te(τ)dτdtde(t)u(k)u(k−1)KiKdKIKDΔuk=u(k)−u(k−1)=Kpe(t)+Ki∫0te(t)dt+Kddtde(t)≈kτ(k=0,1,2,...)≈u(k)≈e(k)≈τj=0∑ke(jτ)=τj=0∑kej≈τe(kτ)−e((k−1)τ)=τek−ek−1=Kpe(k)+Kiτj=0∑ke(j)+Kdτe(k)−e(k−1)=Kpe(k−1)+Kiτj=0∑k−1e(j)+Kdτe(k−1)−e(k−2)=TiKp=KpTd=TiKp∗τ=Kiτ=KpτTd=τKD=Kp(e(k)−e(k−1)+Tiτe(k)+Tdτe(k)−2e(k−1)+e(k−2))=Kp(1+Tiτ+τTd)e(k)−Kp(1+τ2Td)e(k−1)+KpτTde(k−2)=Ae(k)+Be(k−1)+Ce(k−2)(1-1)(1-2)(1-3)(1-4)(1-5)(1-6)
4 双 S 型
4.1 介绍
双S型速度规划采用两段线性区间组合的方法解决加速度不连续的问题,线性段端点处采用抛物线过渡的方法,保证连接处的加速度曲线连续。从而减少机械系统的抖动。
双S型规划也叫铃型规划(Bell)、七段S型速度规划。


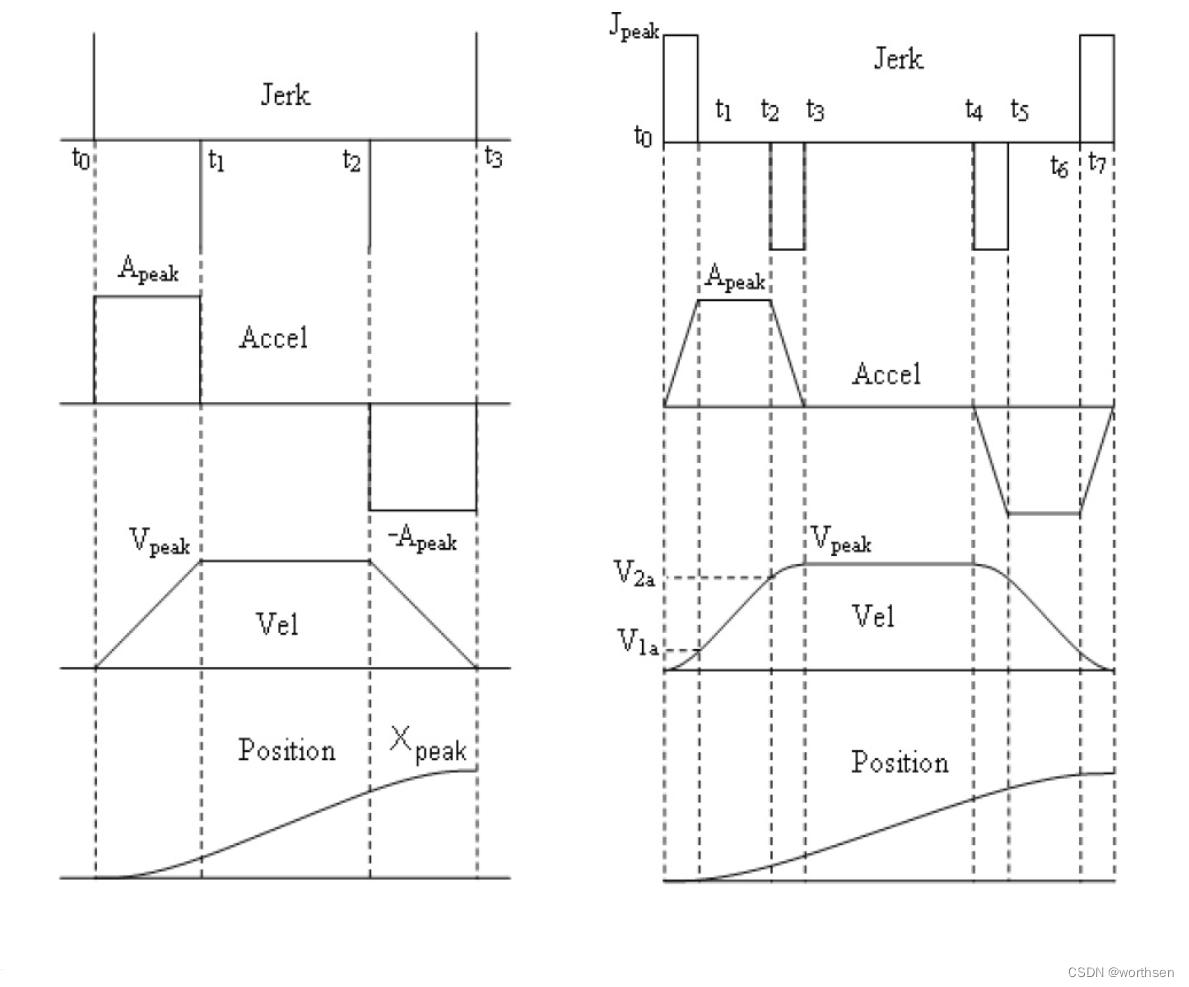
4.2 双S模型(7段S型)
如下参考:
- 《ADAPTIVE MOTION PLANNING FOR A MOBILE ROBOT》CLARA GIFRE OLIVERAS. Master’s Thesis Degree Programme in Computer Science and Engineering June 2013
- 一文教你快速搞懂速度曲线规划之S形曲线(超详细+图文+推导+附件代码)
- 【自动驾驶】运动规划丨速度规划丨T型/S型速度曲线
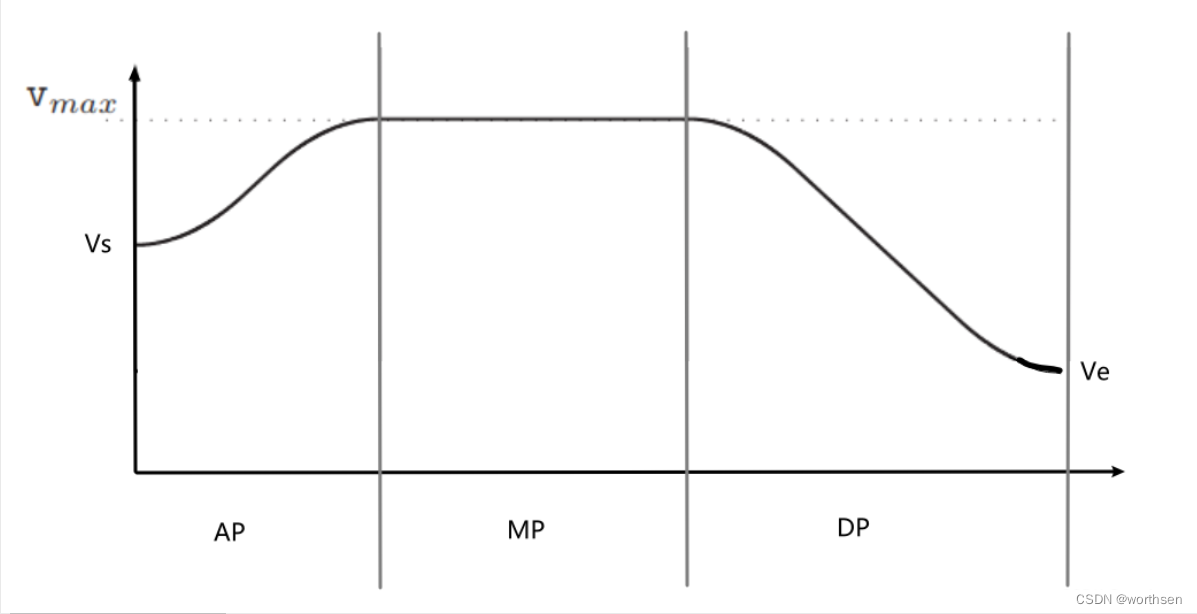
观察上述速度曲线图,可以将整个运动可分为A M D三个过程,分别是:
- 加速阶段(Acceleration Phase, AP)
- 最大速度阶段(Maximum Phase, MP)
- 减速阶段(Deceleration Phase, DP)
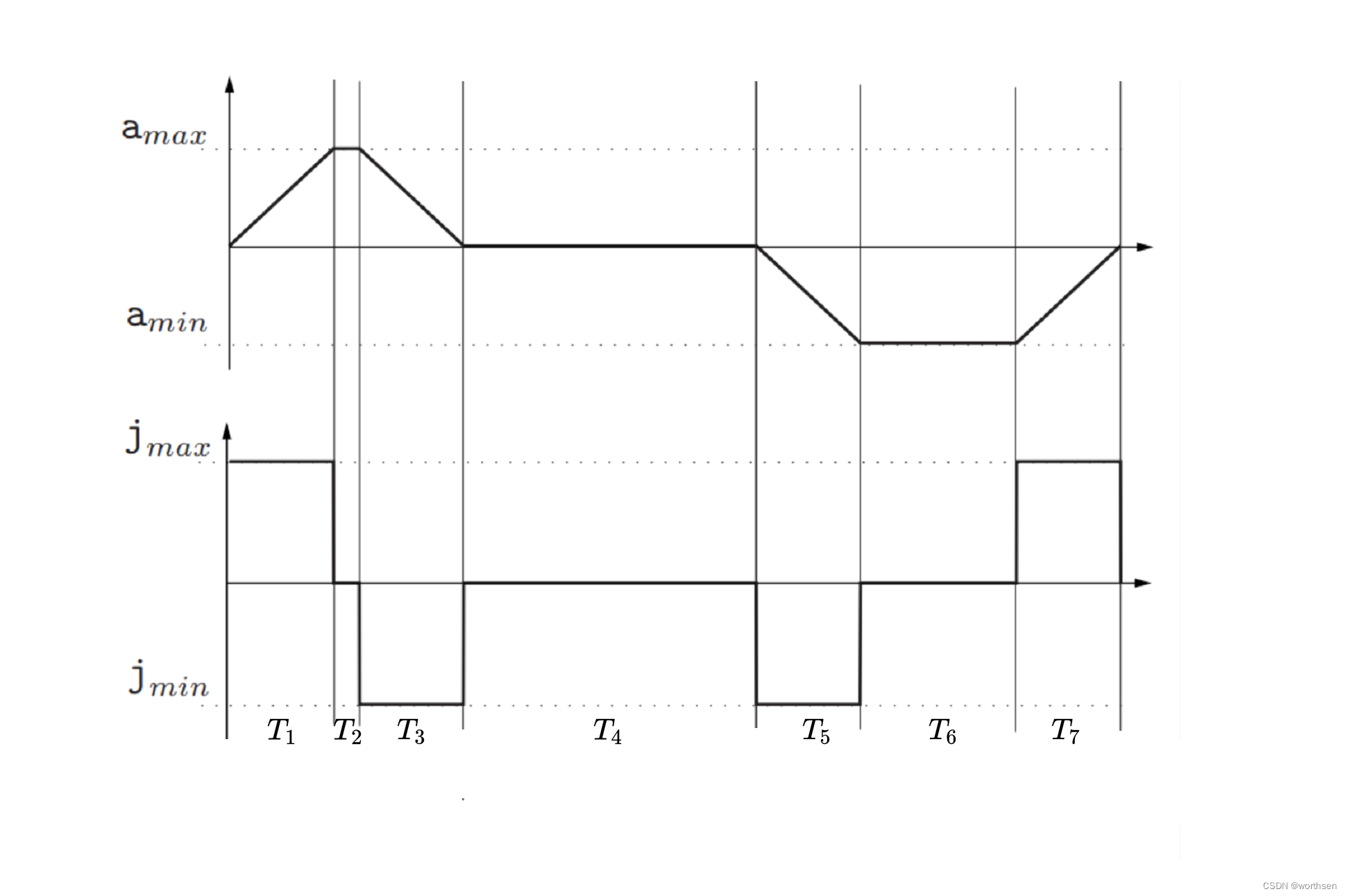
规划参数
J:Jerk,加加速度;
A
m
a
x
A_{max}
Amax:最大加速度;
D
m
a
x
D_{max}
Dmax:最大减速度;
V
s
V_s
Vs:系统初速度;
V
e
V_e
Ve:系统末速度;
T
i
(
i
=
1
,
2
,
.
.
,
7
)
T_i(i=1,2,..,7)
Ti(i=1,2,..,7):表示各个阶段的运行时间;
v
i
(
i
=
1
,
2
,
.
.
,
7
)
v_i(i=1,2,..,7)
vi(i=1,2,..,7):表示各个运行结束时的速度值;
τ
i
=
t
−
t
i
−
1
,
(
i
=
1
,
2
,
.
.
,
7
)
\tau_i = t - t_{i - 1}, (i=1,2,..,7)
τi=t−ti−1,(i=1,2,..,7):
τ
i
∈
(
t
i
−
1
,
t
i
)
\tau_i \in (t_{i - 1}, t_i)
τi∈(ti−1,ti)
F:系统可以达到的最大进给速度;
算法公式
j ( t ) = { J 0 ≤ t < t 1 0 t 1 ≤ t < t 2 − J t 2 ≤ t < t 3 0 t 3 ≤ t < t 4 − J t 4 ≤ t < t 5 0 t 5 ≤ t < t 6 J t 6 ≤ t < t 7 a ( t ) = { a 0 + J τ 1 0 ≤ t < t 1 A m a x t 1 ≤ t < t 2 A m a x − J τ 3 t 2 ≤ t < t 3 0 t 3 ≤ t < t 4 − J τ 5 t 4 ≤ t < t 5 − D m a x t 5 ≤ t < t 6 − D m a x + J τ 7 t 6 ≤ t < t 7 v ( t ) = { v 0 + a 0 τ 1 + 1 2 J τ 1 2 0 ≤ t < t 1 v 1 = v 0 + a 0 T 1 + 1 2 J T 1 2 v 1 + A m a x τ 2 t 1 ≤ t < t 2 v 2 = v 1 + A m a x T 2 v 2 + A m a x τ 3 − 1 2 J τ 3 2 t 2 ≤ t < t 3 v 3 = v 2 + A m a x T 3 − 1 2 J T 3 2 v 3 t 3 ≤ t < t 4 v 4 = v 3 v 4 − 1 2 J τ 5 2 t 4 ≤ t < t 5 v 5 = v 4 − 1 2 J T 5 2 v 5 − D m a x τ 6 t 5 ≤ t < t 6 v 6 = v 5 − D m a x T 6 v 6 − D m a x τ 7 + 1 2 J τ 7 2 t 6 ≤ t < t 7 v 7 = v 6 − D m a x T 7 + 1 2 J T 7 2 s ( t ) = { s 0 + v 0 τ 1 + 1 2 a 0 τ 1 2 + 1 6 J τ 1 3 0 ≤ t < t 1 s 1 = s 0 + v 0 T 1 + 1 2 a 0 T 1 2 + 1 6 J T 1 3 s 1 + v 1 τ 2 + 1 2 A m a x τ 2 2 t 1 ≤ t < t 2 s 2 = s 1 + v 1 T 2 + 1 2 A m a x T 2 2 s 2 + v 2 τ 3 + 1 2 A m a x τ 3 2 − 1 6 J τ 3 3 t 2 ≤ t < t 3 s 3 = s 2 + v 2 T 3 + 1 2 A m a x T 3 2 − 1 6 J T 3 3 s 3 + v 3 τ 4 t 3 ≤ t < t 4 v 4 = s 3 + v 3 T 4 s 4 + v 4 τ 5 − 1 6 J τ 5 3 t 4 ≤ t < t 5 s 5 = s 4 + v 4 T 5 − 1 6 J T 5 3 s 5 + v 5 τ 6 − 1 2 D m a x τ 6 2 t 5 ≤ t < t 6 s 6 = s 5 + v 5 T 6 − 1 2 D m a x T 6 2 s 6 + v 6 τ 7 − 1 2 D m a x τ 7 2 + 1 6 J τ 7 3 t 6 ≤ t < t 7 s 7 = s 6 + v 6 T 7 − 1 2 D m a x T 7 2 + 1 6 J T 7 3 \begin{align} j(t) & = \tag{2-1} \begin{cases} J &\qquad \qquad 0 \leq t < t_1 \\ 0 &\qquad \qquad t_1 \leq t < t_2 \\ -J &\qquad \qquad t_2 \leq t < t_3 \\ 0 &\qquad \qquad t_3 \leq t < t_4 \\ -J &\qquad \qquad t_4 \leq t < t_5 \\ 0 &\qquad \qquad t_5 \leq t < t_6 \\ J &\qquad \qquad t_6 \leq t < t_7 \\ \end{cases} \\ a(t) & = \tag{2-2} \begin{cases} a_0 + J \tau_1 &\qquad 0 \leq t < t_1 \\ A_{max} &\qquad t_1 \leq t < t_2 \\ A_{max} - J \tau_3 &\qquad t_2 \leq t < t_3 \\ 0 &\qquad t_3 \leq t < t_4 \\ -J \tau_5 &\qquad t_4 \leq t < t_5 \\ -D_{max} &\qquad t_5 \leq t < t_6 \\ -D_{max} + J \tau_7 &\qquad t_6 \leq t < t_7 \\ \end{cases} \\ v(t) & = \tag{2-3} \begin{cases} v_0 + a_0 \tau_1 + \frac{1}{2}J \tau^2_1 & 0 \leq t < t_1 \qquad v_1 = v_0 + a_0 T_1 + \frac{1}{2}J T^2_1 \\ v_1 + A_{max} \tau_2 & t_1 \leq t < t_2 \qquad v_2 = v_1 + A_{max}T_2 \\ v_2 + A_{max} \tau_3 - \frac{1}{2}J \tau^2_3 & t_2 \leq t < t_3 \qquad v_3 = v_2 + A_{max}T_3 - \frac{1}{2}J T^2_3 \\ v_3 & t_3 \leq t < t_4 \qquad v_4 = v_3 \\ v_4 - \frac{1}{2}J \tau^2_5 & t_4 \leq t < t_5 \qquad v_5 = v_4 - \frac{1}{2}J T^2_5\\ v_5 - D_{max}\tau_6 & t_5 \leq t < t_6 \qquad v_6 = v_5 - D_{max} T_6 \\ v_6 -D_{max}\tau_7 + \frac{1}{2}J \tau^2_7 & t_6 \leq t < t_7 \qquad v_7 = v_6 - D_{max}T_7 + \frac{1}{2}J T^2_7\\ \end{cases} \\ s(t) & = \tag{2-4} \begin{cases} s_0 + v_0 \tau_1 + \frac{1}{2}a_0 \tau^2_1 + \frac{1}{6}J \tau^3_1 & 0 \leq t < t_1 \qquad s_1 = s_0 + v_0 T_1 + \frac{1}{2}a_0 T^2_1 + \frac{1}{6}J T^3_1 \\ s_1 + v_1 \tau_2 + \frac{1}{2}A_{max} \tau^2_2 & t_1 \leq t < t_2 \qquad s_2 =s_1 + v_1 T_2 + \frac{1}{2} A_{max}T^2_2 \\ s_2 + v_2 \tau_3 + \frac{1}{2}A_{max} \tau^2_3 - \frac{1}{6}J \tau^3_3 & t_2 \leq t < t_3 \qquad s_3 = s_2 + v_2 T_3 + \frac{1}{2} A_{max}T^2_3 - \frac{1}{6}J T^3_3 \\ s_3 + v_3 \tau_4 & t_3 \leq t < t_4 \qquad v_4 = s_3 + v_3T_4 \\ s_4 + v_4 \tau_5 - \frac{1}{6}J \tau^3_5 & t_4 \leq t < t_5 \qquad s_5 = s_4 + v_4 T_5 - \frac{1}{6}J T^3_5\\ s_5 + v_5 \tau_6 - \frac{1}{2}D_{max}\tau^2_6 & t_5 \leq t < t_6 \qquad s_6 = s_5 + v_5 T_6 - \frac{1}{2}D_{max} T^2_6 \\ s_6 + v_6 \tau_7 -\frac{1}{2} D_{max}\tau^2_7 + \frac{1}{6}J \tau^3_7 & t_6 \leq t < t_7 \qquad s_7 = s_6 + v_6T_7 - \frac{1}{2}D_{max}T^2_7 + \frac{1}{6}J T^3_7\\ \end{cases} \\ \end{align} j(t)a(t)v(t)s(t)=⎩ ⎨ ⎧J0−J0−J0J0≤t<t1t1≤t<t2t2≤t<t3t3≤t<t4t4≤t<t5t5≤t<t6t6≤t<t7=⎩ ⎨ ⎧a0+Jτ1AmaxAmax−Jτ30−Jτ5−Dmax−Dmax+Jτ70≤t<t1t1≤t<t2t2≤t<t3t3≤t<t4t4≤t<t5t5≤t<t6t6≤t<t7=⎩ ⎨ ⎧v0+a0τ1+21Jτ12v1+Amaxτ2v2+Amaxτ3−21Jτ32v3v4−21Jτ52v5−Dmaxτ6v6−Dmaxτ7+21Jτ720≤t<t1v1=v0+a0T1+21JT12t1≤t<t2v2=v1+AmaxT2t2≤t<t3v3=v2+AmaxT3−21JT32t3≤t<t4v4=v3t4≤t<t5v5=v4−21JT52t5≤t<t6v6=v5−DmaxT6t6≤t<t7v7=v6−DmaxT7+21JT72=⎩ ⎨ ⎧s0+v0τ1+21a0τ12+61Jτ13s1+v1τ2+21Amaxτ22s2+v2τ3+21Amaxτ32−61Jτ33s3+v3τ4s4+v4τ5−61Jτ53s5+v5τ6−21Dmaxτ62s6+v6τ7−21Dmaxτ72+61Jτ730≤t<t1s1=s0+v0T1+21a0T12+61JT13t1≤t<t2s2=s1+v1T2+21AmaxT22t2≤t<t3s3=s2+v2T3+21AmaxT32−61JT33t3≤t<t4v4=s3+v3T4t4≤t<t5s5=s4+v4T5−61JT53t5≤t<t6s6=s5+v5T6−21DmaxT62t6≤t<t7s7=s6+v6T7−21DmaxT72+61JT73(2-1)(2-2)(2-3)(2-4)
T 1 = { A m a x J F ≥ v s + A m a x 2 J F − v s J F < v s + A m a x 2 J T 2 = { F − v s A m a x − A m a x J F ≥ v s + A m a x 2 J 0 F < v s + A m a x 2 J T 5 = { D m a x J F ≥ v e + D m a x 2 J F − v e J F < v e + D m a x 2 J T 6 = { F − v e D m a x − D m a x J F ≥ v s + D m a x 2 J 0 F < v e + D m a x 2 J \begin{align} T_1 & = \tag{2-1} \begin{cases} \frac{A_{max}}{J} &\qquad F \geq v_s + \frac{A^2_{max}}{J} \\ \sqrt{\frac{F - v_s}{J}} &\qquad F < v_s + \frac{A^2_{max}}{J} \end{cases} \\ T_2 & = \tag{2-2} \begin{cases} \frac{F - v_s}{A_{max}}- \frac{A_{max}}{J} & F \geq v_s + \frac{A^2_{max}}{J} \\ 0 & F < v_s + \frac{A^2_{max}}{J} \end{cases} \\ T_5 & = \tag{2-3} \begin{cases} \frac{D_{max}}{J} &\qquad F \geq v_e + \frac{D^2_{max}}{J} \\ \sqrt{\frac{F - v_e}{J}} &\qquad F < v_e + \frac{D^2_{max}}{J} \end{cases} \\ T_6 & = \tag{2-4} \begin{cases} \frac{F - v_e}{D_{max}} - \frac{D_{max}}{J} & F \geq v_s + \frac{D^2_{max}}{J} \\ 0 & F < v_e + \frac{D^2_{max}}{J} \end{cases} \\ \end{align} T1T2T5T6=⎩ ⎨ ⎧JAmaxJF−vsF≥vs+JAmax2F<vs+JAmax2={AmaxF−vs−JAmax0F≥vs+JAmax2F<vs+JAmax2=⎩ ⎨ ⎧JDmaxJF−veF≥ve+JDmax2F<ve+JDmax2={DmaxF−ve−JDmax0F≥vs+JDmax2F<ve+JDmax2(2-1)(2-2)(2-3)(2-4)
v 1 = v s + 1 2 J T 1 2 v 2 = v 1 + J T 1 T 2 v 3 = v s + J T 1 2 + J T 1 T 2 v 4 = v 3 v 5 = v 4 − 1 2 J T 5 2 v 6 = v 5 − J T 5 T 6 \begin{align} v_1 & = v_s + \frac{1}{2}JT^2_1 \notag \\ v_2 &= v_1 + J T_1 T_2 \notag \\ v_3 &= v_s + J T^2_1 + J T_1 T_2 \notag \\ v_4 &= v_3 \tag{2-5} \\ v_5 &= v_4 - \frac{1}{2}J T^2_5 \notag \\ v_6 &= v_5 - J T_5 T_6 \notag \\ \end{align} v1v2v3v4v5v6=vs+21JT12=v1+JT1T2=vs+JT12+JT1T2=v3=v4−21JT52=v5−JT5T6(2-5)
轨迹分类
5 多种速度规划对比 【引用 Marc Pony】
From 速度规划(梯形、余弦、多项式、7段S型、7段修正S型、15段S型、31段S型)
连续性与平滑性:31段S型 > >> 多项式 ≈ 15段S型 > >> 7段修正S型 > >> 余弦 > >> 7段S型 > >> 梯形;
可控性:31段S型> >> 15段S型 > >> 7段修正S型 = 7段S型 = 多项式 > >> 余弦 = == 梯形;
规划总时间:多项式 > >> 余弦 > >> 31段S型 > >> 15段S型 > >> 7段修正S型 > >> 7段S型 > >> 梯形;
算法计算量:31段S型 > >> 15段S型 > >> 7段修正S型 > >> 7段S型 > >> 多项式 ≈ 余弦 > >> 梯形。
根据对比,7种速度规划算法大致可分为低中高端三档。
低档:梯形、余弦
中档:多项式、7段S型、7段修正S型
高档:15段S型、31段S型
| 规划模型 | 描述 | 速度 加速度 高阶导数 | 规划时间 | 算法难度 计算量 | 图示 |
|---|---|---|---|---|---|
| 梯形 | 位置平滑 速度连续但不平滑 加速度跳变 二次加速度出现无穷大跳变 | 速度、加速度可控 更高阶不可控 | 所有速度规划算法中 规划时间最短 | 算法最简单 计算量最小 | 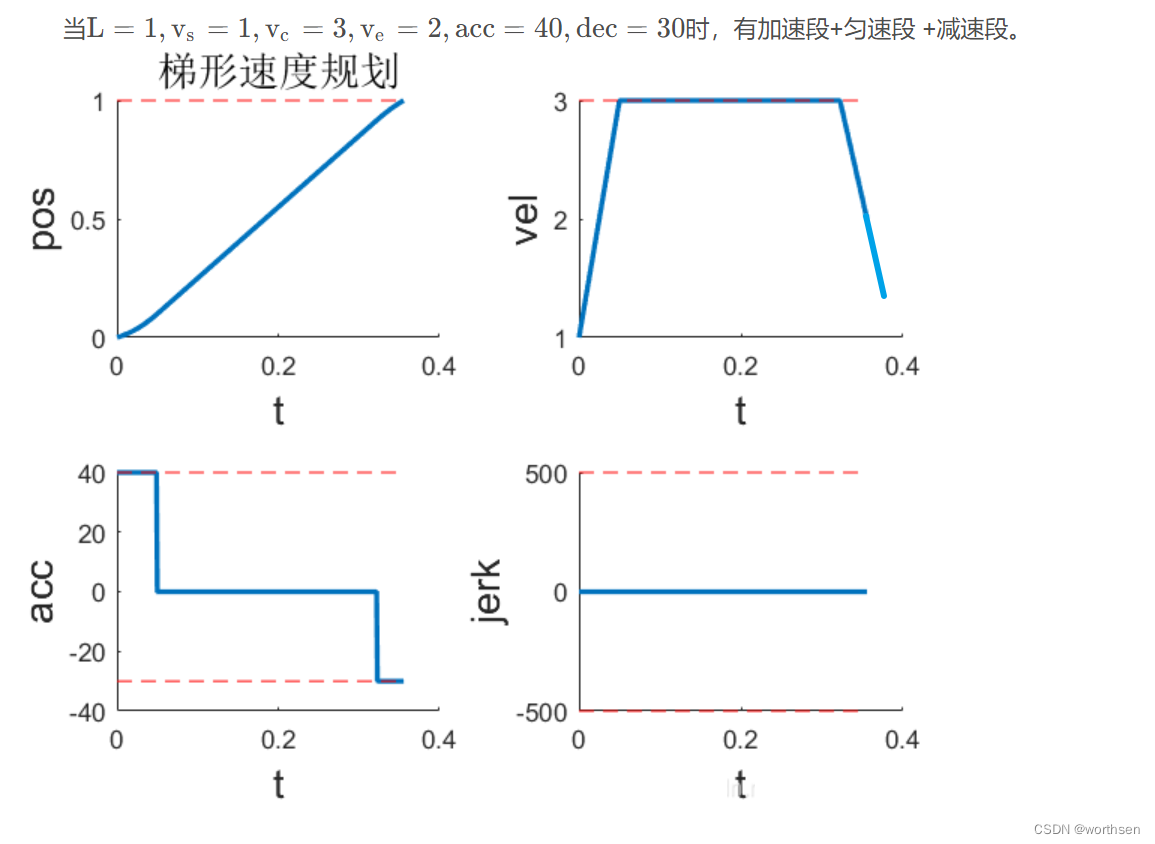 |
| 余弦 | 位置平滑 速度平滑 加速度连续但不够平滑 二次加速度跳变 | 速度、加速度可控 更高阶不可控 | 规划时间较长 | 算法较简单 计算量较小 | 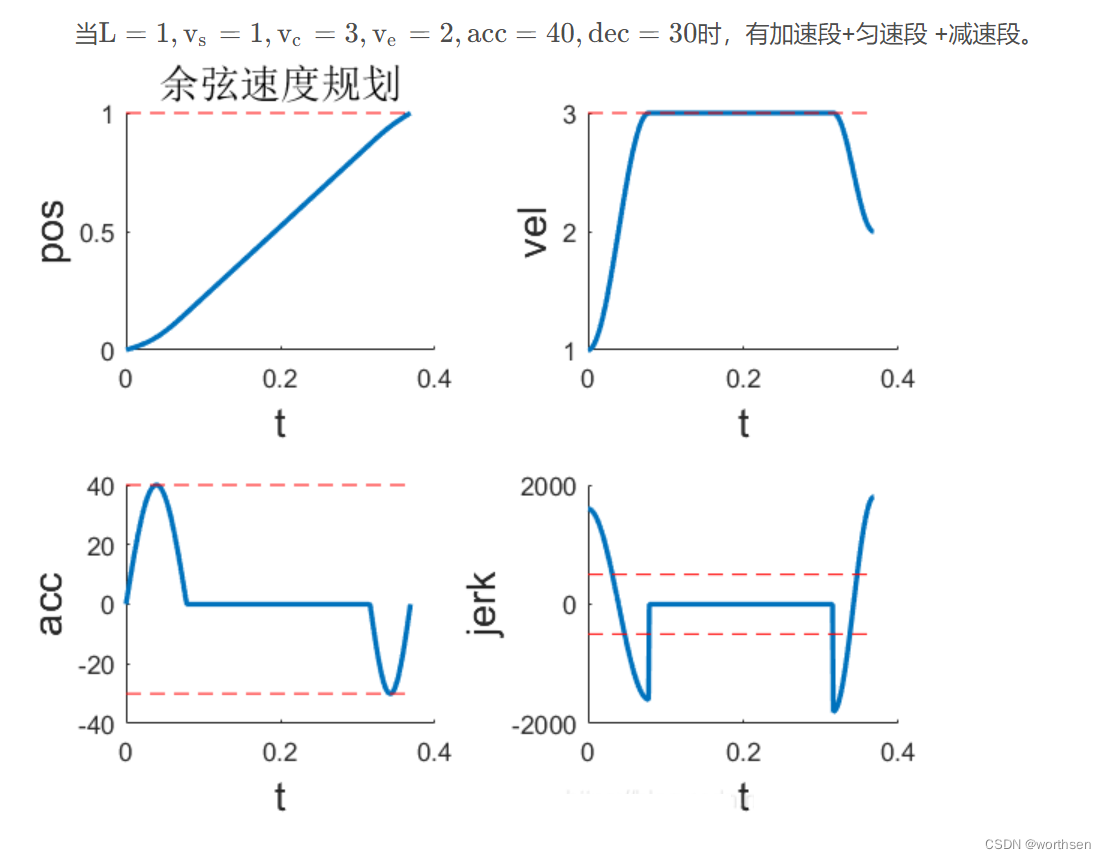 |
| 多项式 | 位置平滑 速度平滑 加速度平滑 二次加速度连续但不够平滑 三次加速度跳变 | 速度、加速度可控 二次加速度可控 更高阶不可控 | 规划时间长 | 算法较简单 计算量较小 | 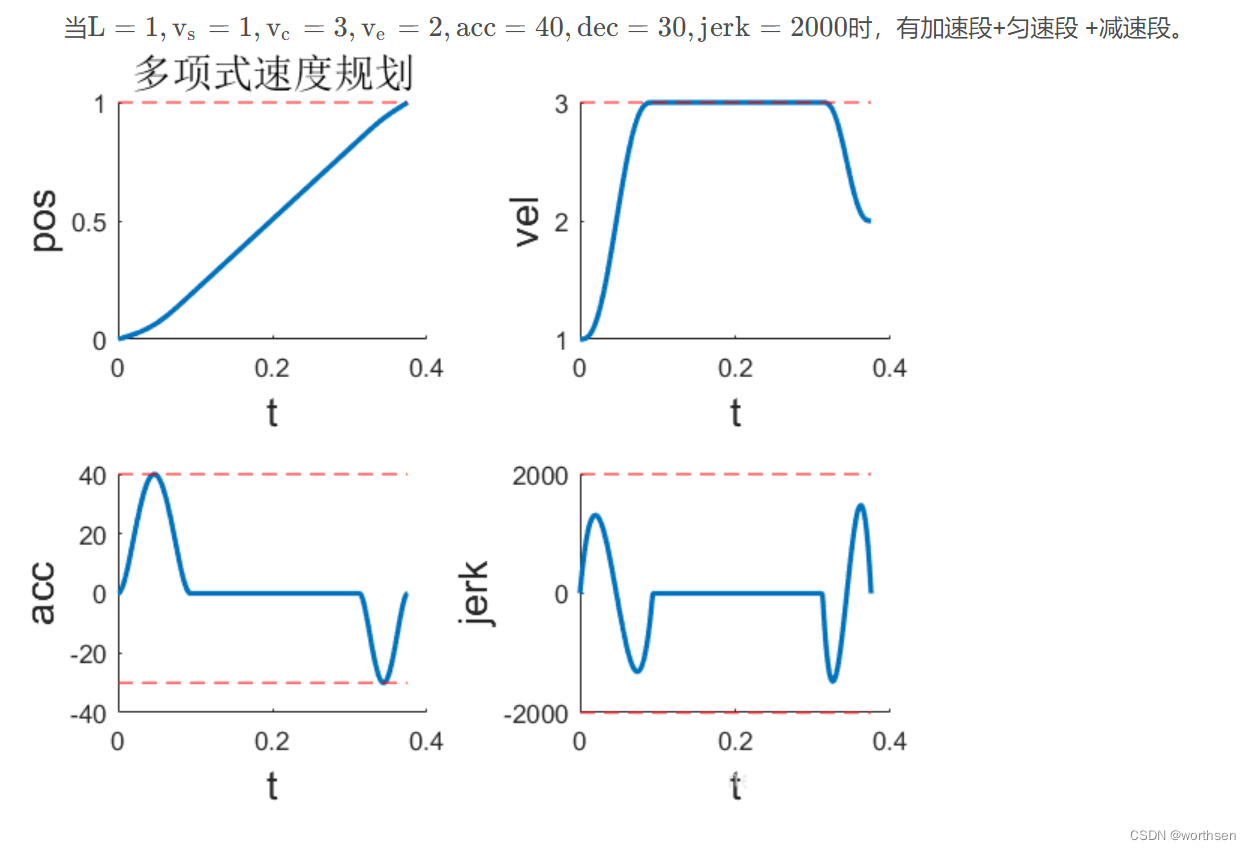 |
| 7段S型 | 位置平滑 速度平滑 加速度连续但不平滑 二次加速度跳变 | 速度、加速度可控 二次加速度可控 更高阶不可控 | 规划时间较短 | 算法稍复杂 计算量稍大 | 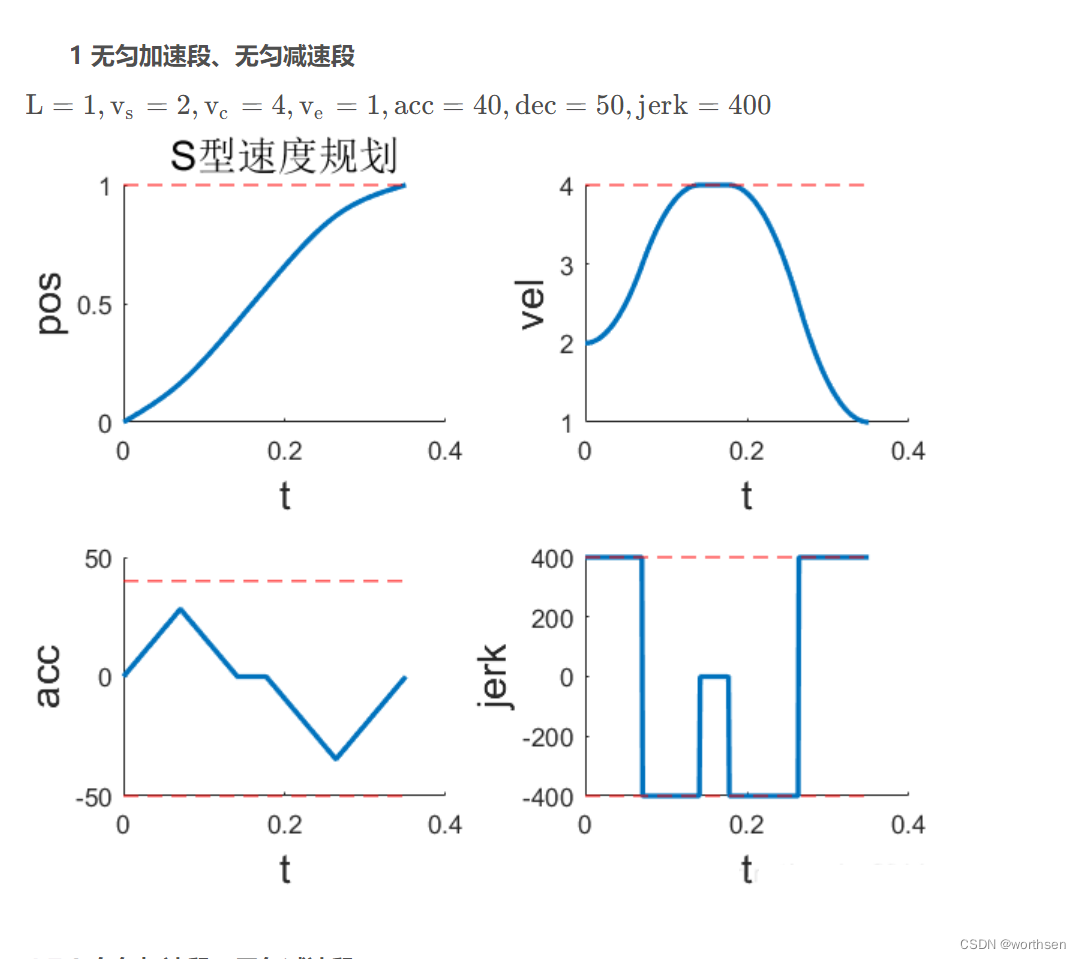 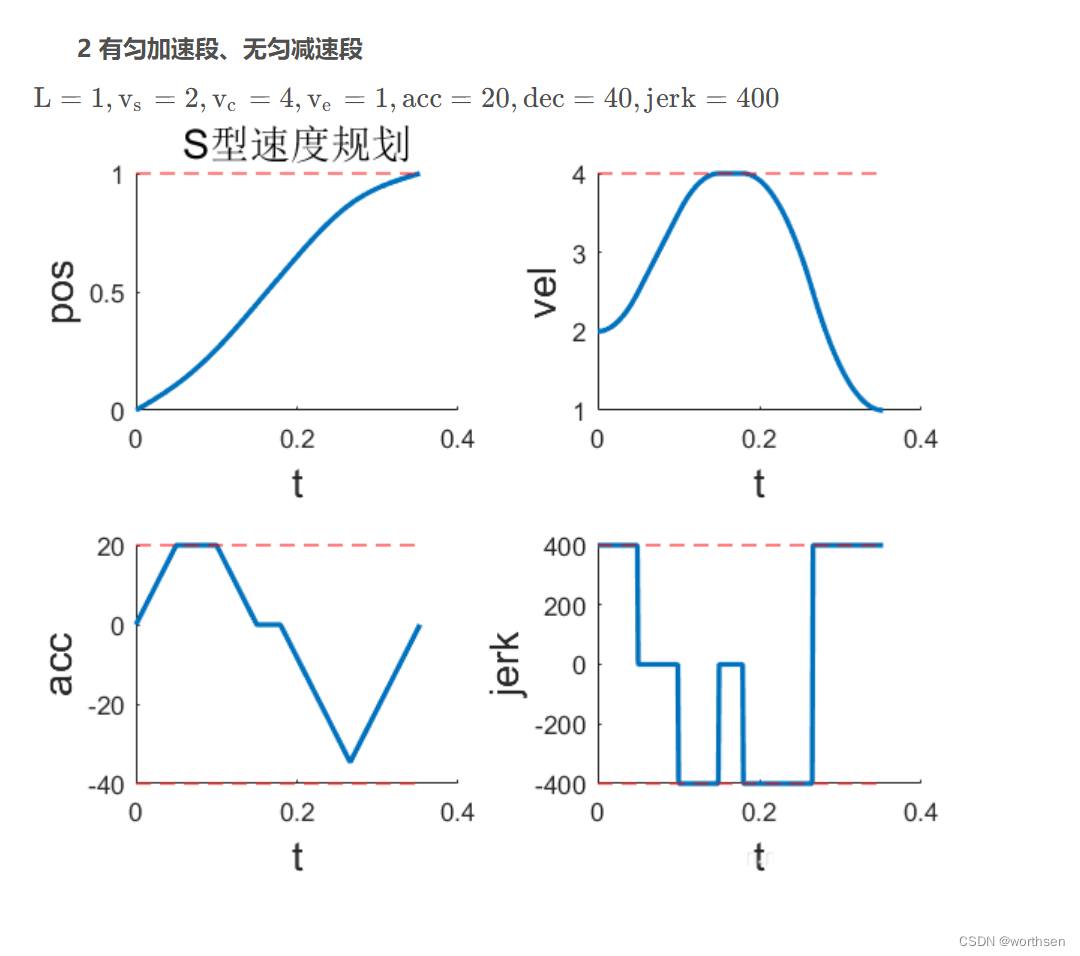 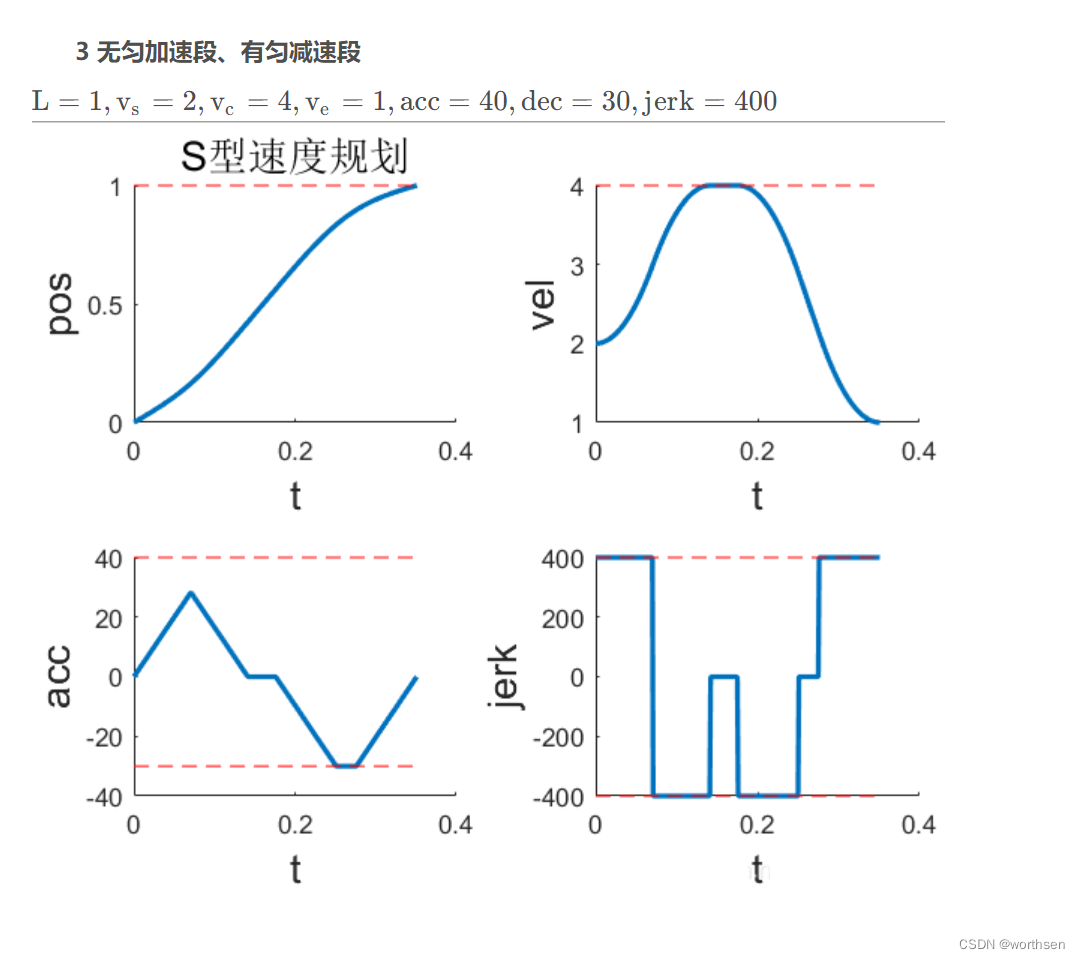 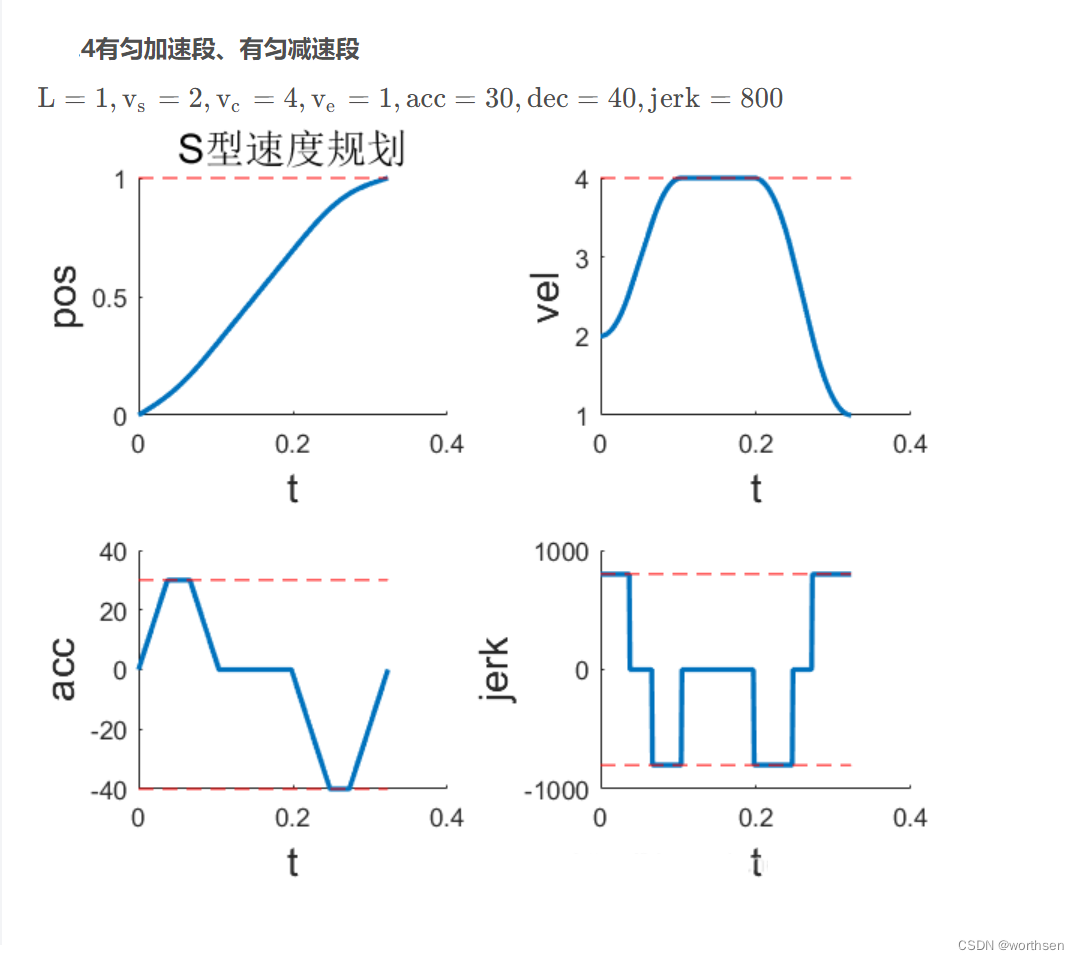 |
| 7段修正S型 | 位置平滑,速度平滑 加速度连续但不够平滑 二次加速度跳变 | 速度、加速度可控 二次加速度可控 更高阶不可控 | 规划时间较短 | 算法稍复杂 计算量稍大 | 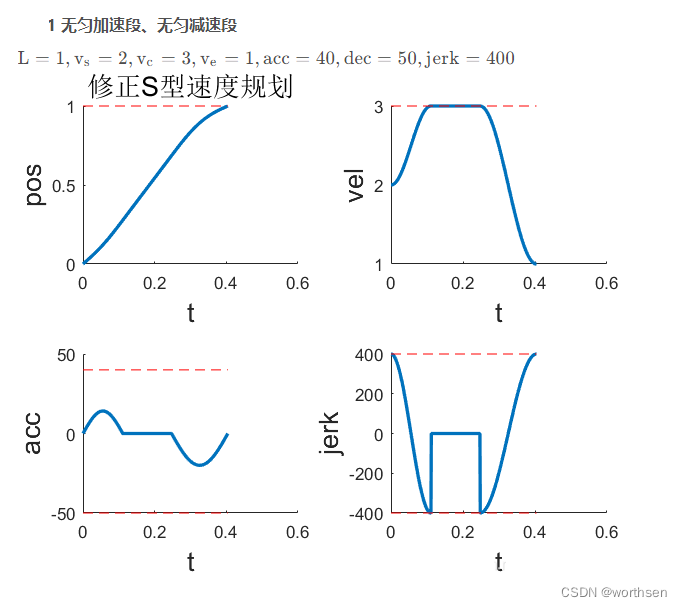 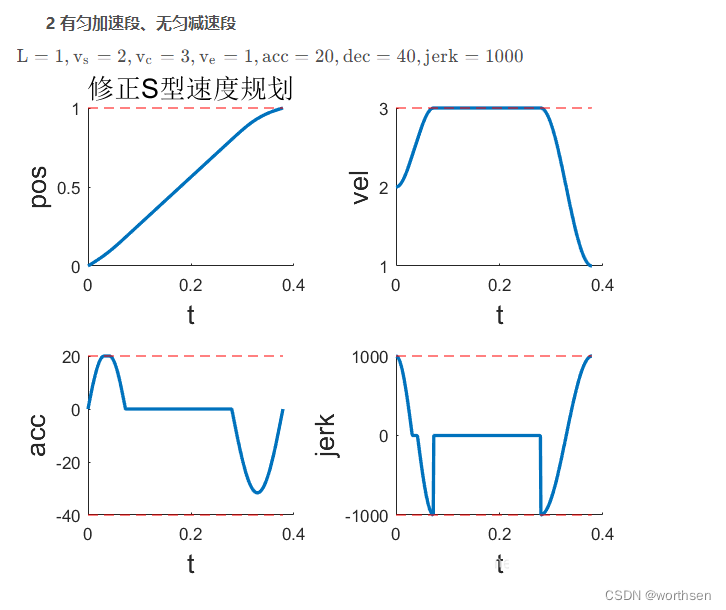 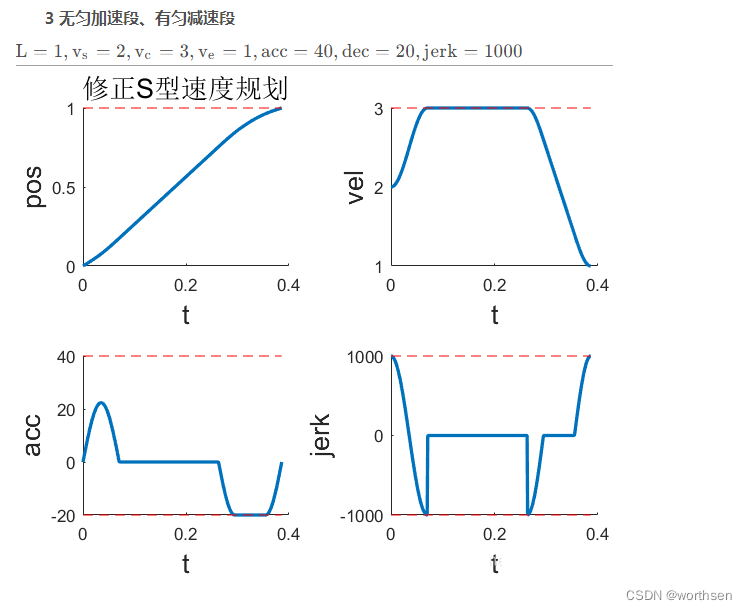 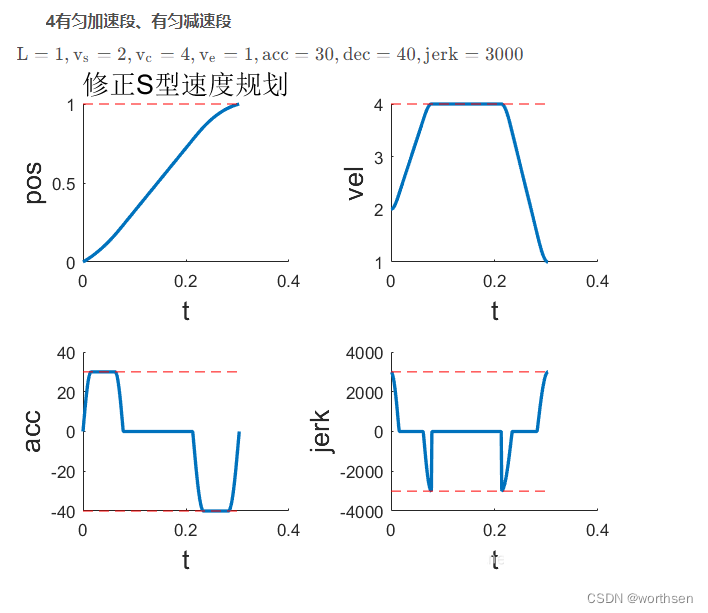 |
| 15段S型 | 位置平滑,速度平滑,加速度平滑 二次加速度连续但不平滑 三次加速度跳变 | 速度、加速度可控 二次加速度可控 三次加速度可控 四次加速度不可控 | 规划时间稍长 | 算法较复杂 计算量较大 | 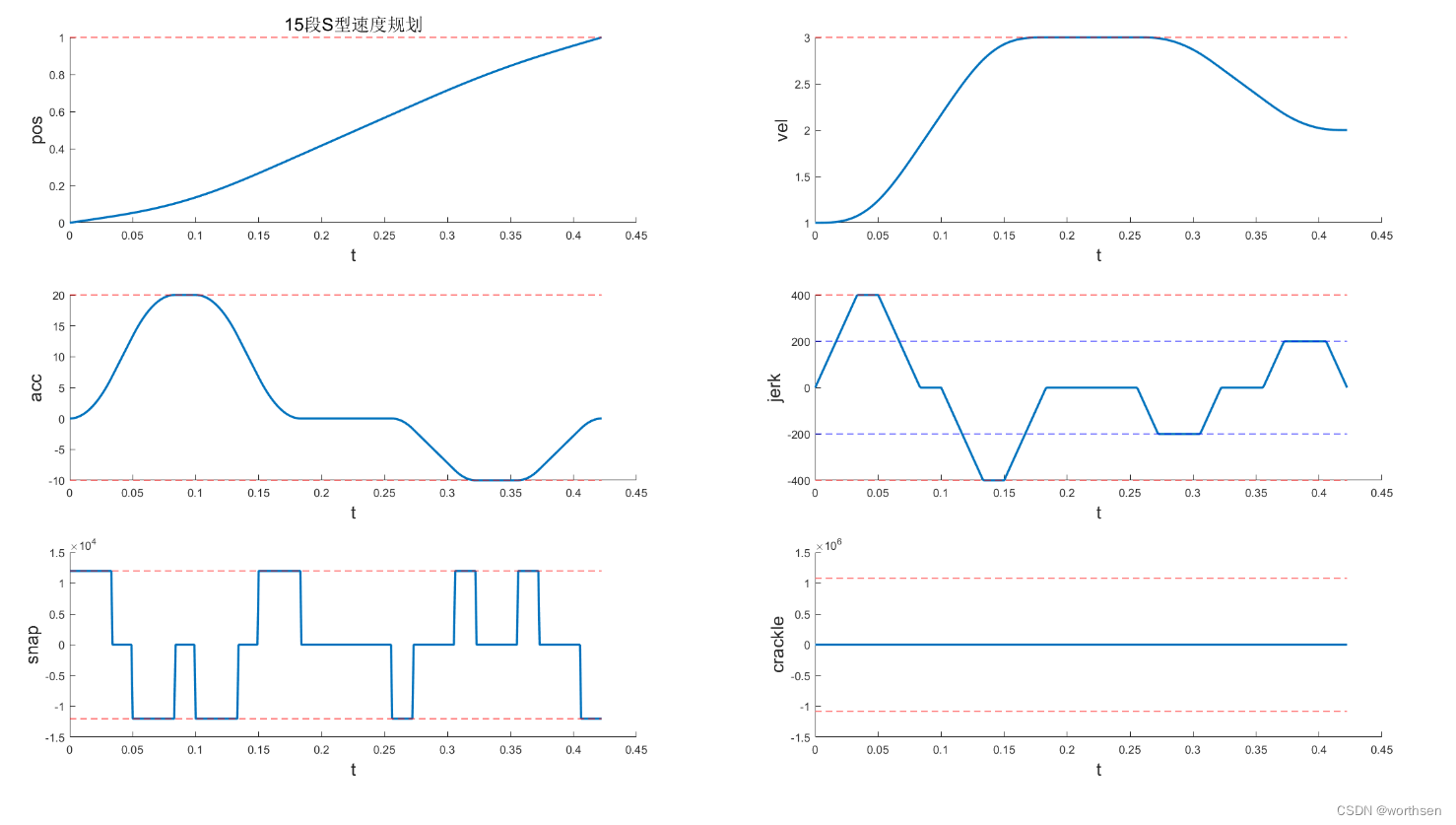 |
| 31段S型 | 位置平滑,速度平滑 加速度平滑 二次加速度平滑 三次加速度连续但不平滑 四次加速度跳变 | 位置的各阶导皆可控 | 规划时间稍长 | 算法较复杂 计算量较大 | 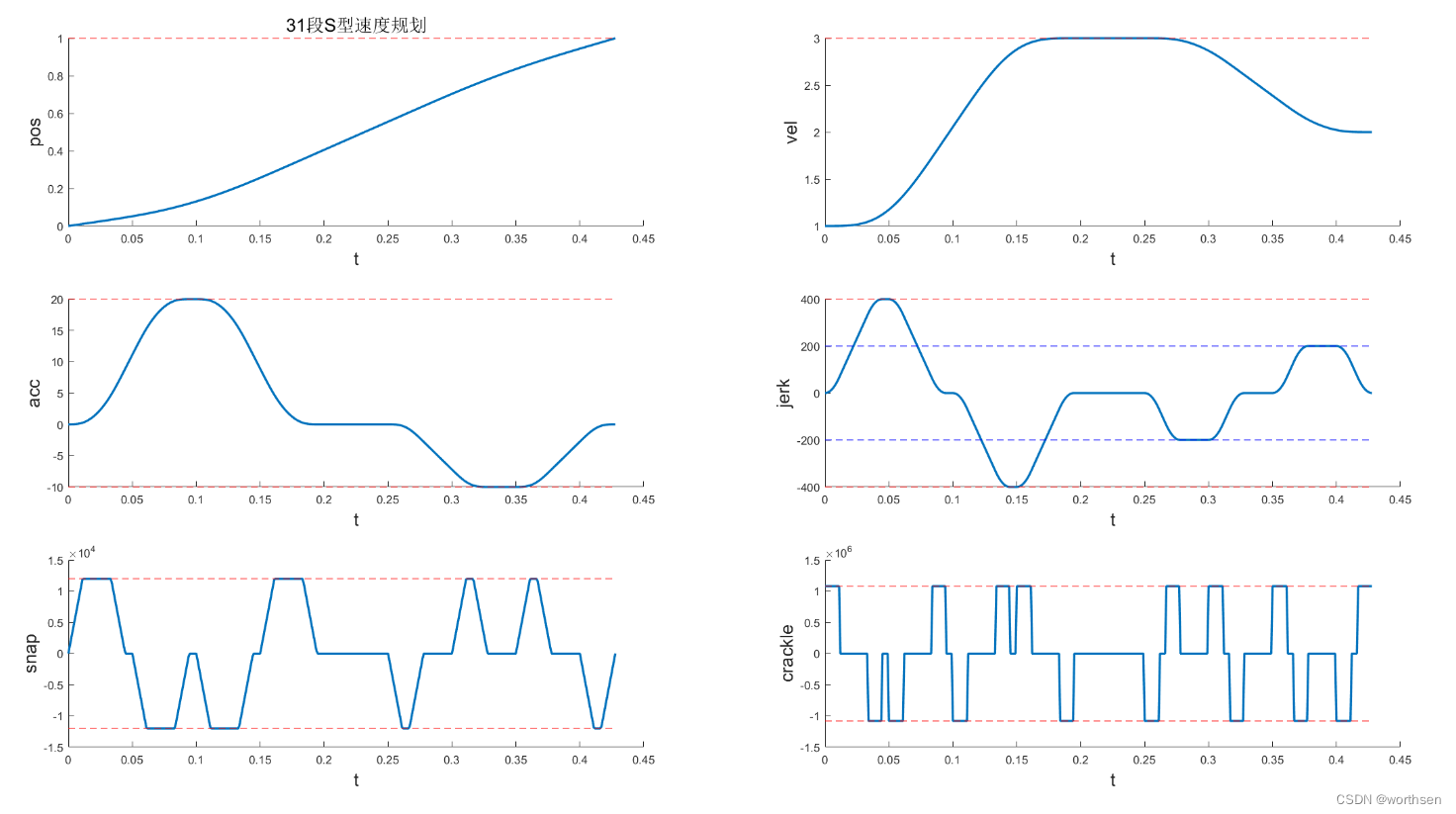 |
6 示例
基于PID控制策略的机械臂轨迹跟踪控制
基于PID控制策略的机械臂轨迹跟踪控制
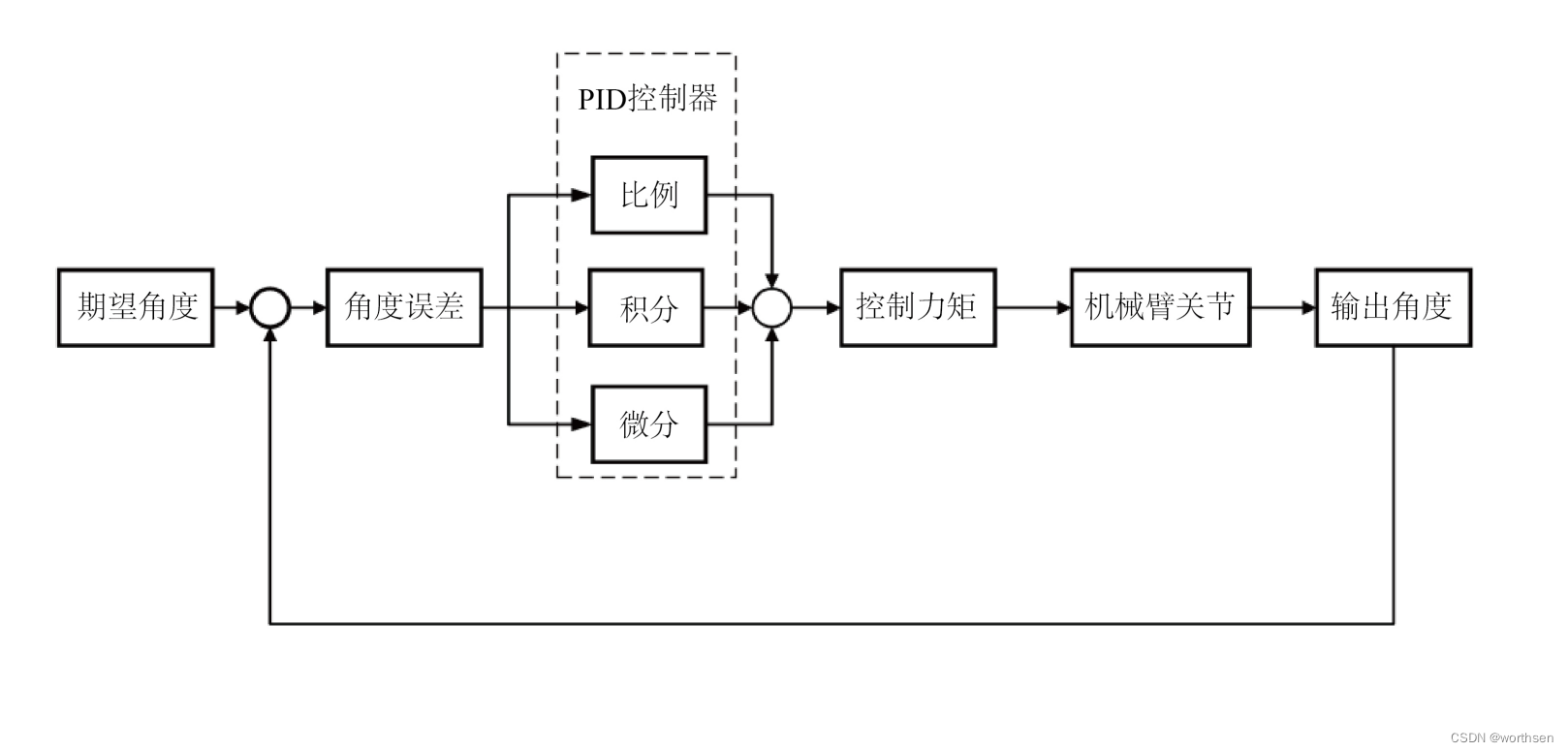
Kinematically Constrained Jerk–Continuous S-Curve Trajectory Planning in Joint Space for Industrial Robots
Kinematically Constrained Jerk–Continuous S-Curve Trajectory Planning in Joint Space for Industrial Robots
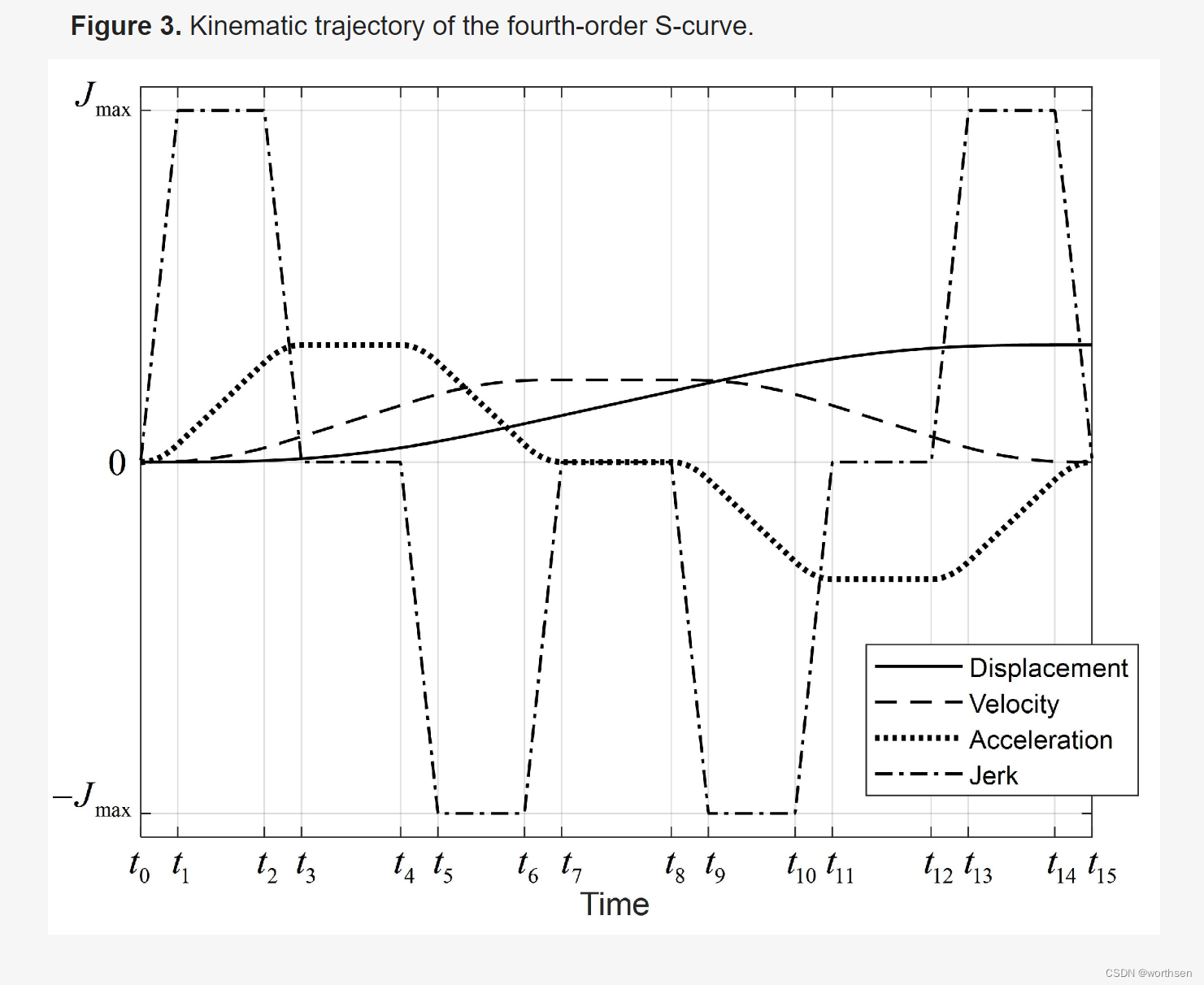
Time-Optimal Asymmetric S-Curve Trajectory Planning of Redundant Manipulators under Kinematic Constraints
Time-Optimal Asymmetric S-Curve Trajectory Planning of Redundant Manipulators under Kinematic Constraints
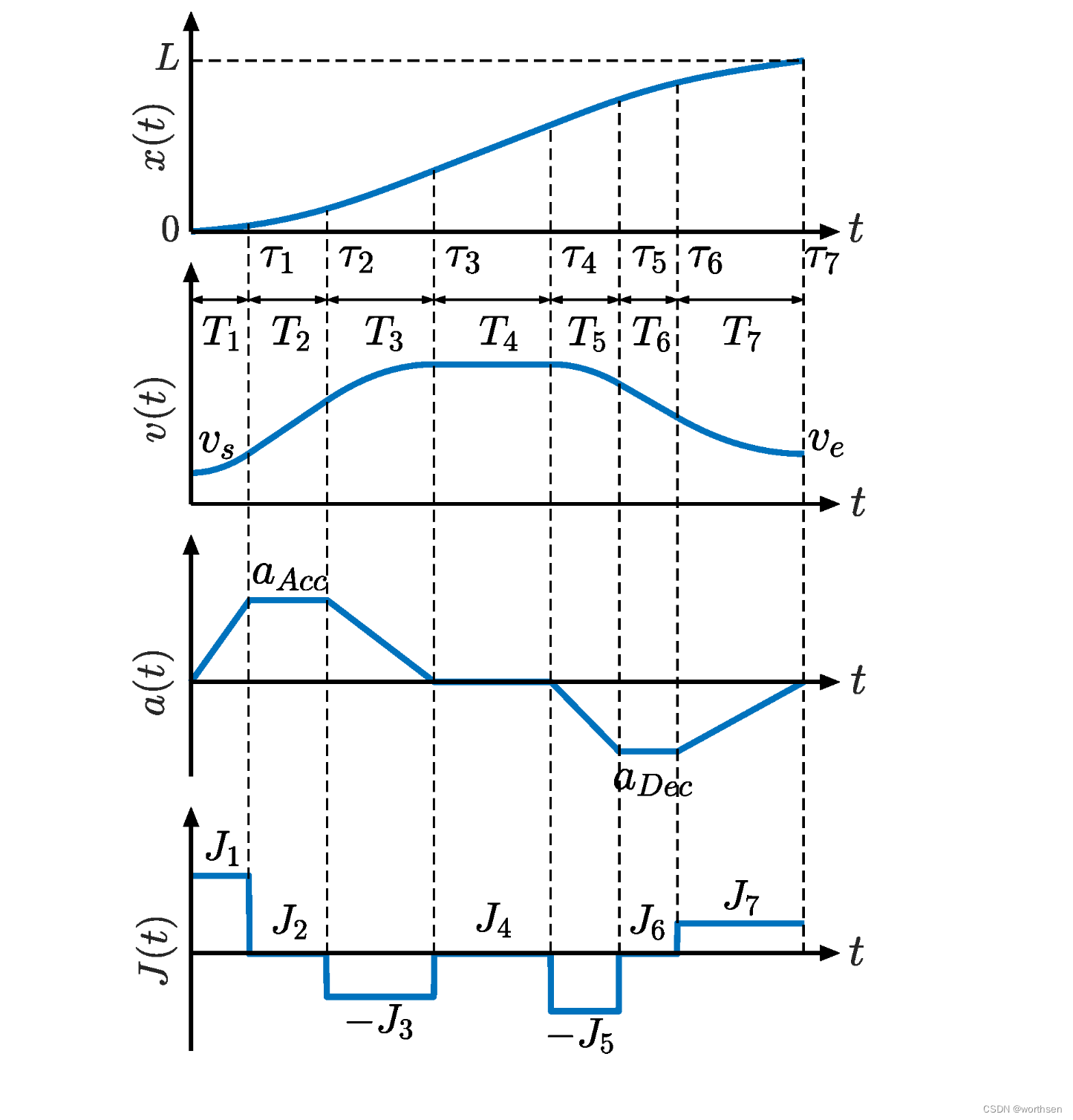
参考
1、运动控制介绍
2、PID 算法详细介绍
3、《ADAPTIVE MOTION PLANNING FOR A MOBILE ROBOT》CLARA GIFRE OLIVERAS. Master’s Thesis
Degree Programme in Computer Science and Engineering June 2013
4、速度规划(梯形、余弦、多项式、7段S型、7段修正S型、15段S型、31段S型)
5、田军锋, 林浒, 姚壮, et al. 数控系统S型曲线加减速快速规划研究[J]. 小型微型计算机系统, 2013(01):168-172.
6、一文教你快速搞懂速度曲线规划之S形曲线(超详细+图文+推导+附件代码)
7、On Algorithms for Planning S-Curve Motion Profiles
Kim Doang Nguyen, Teck-Chew Ng, and I-Ming Chen.On Algorithms for Planning S-Curve Motion Profiles[J]. January 1, 2008.
8、机器人运动学轨迹规划
机器人运动学轨迹规划(一)
机器人运动学轨迹规划(二)----T型曲线规划算法
机器人运动学轨迹规划(三)----S型曲线规划算法
9、Tuning of fractional PID controllers with Ziegler–Nichols-type rules
10、基于PID控制策略的机械臂轨迹跟踪控制
11、无人机目标跟踪与运动控制④——PID轨迹跟踪控制(MATLAB)
12、New S-Curve feature
13、Velocity planning method for position–velocity–time control based on a modified S-shaped acceleration/deceleration algorithm
14、轨迹规划
15、SPMSM控制:根轨迹法设计位置电流双闭环
16、无人车系统(四):轨迹跟踪PID控制
17、APOLLO UDACITY自动驾驶课程笔记——规划、控制
18、多轴插补为什么普遍使用梯形速度曲线? - 韩峰涛(珞石CTO)
19、平滑轨迹插值方法之多项式插值(附代码)
20、【轨迹规划】Trajectory planning for automatic machines and robots
21、倪洪杰, 王宏霞, 俞立. 轮式移动机器人快速轨迹跟踪
22、Kinematically Constrained Jerk–Continuous S-Curve Trajectory Planning in Joint Space for Industrial Robots
23、Time-Optimal Asymmetric S-Curve Trajectory Planning of Redundant Manipulators under Kinematic Constraints
24、【自动驾驶】运动规划丨速度规划丨T型/S型速度曲线
25、七段S形速度曲线轨迹规划
26、双S型速度规划
(一)双S型速度规划 原理
(二)双S型速度规划 曲线形状的讨论
(三)双S型速度规划 C++实现
27、张立先, 李洪波, 高小山, 孙瑞勇. 高速 CNC 加工 S 型加减速方式连续小直线段插补算法
28、两万字简述自动驾驶路径规划的常用算法
29、王斌锐, 王涛, 李正刚, 陈立, 陈迪剑. 多路径段平滑过渡的自适应前瞻位姿插补算法
30、李振娜 , 王涛 , 王斌锐 , 郭振武 , 陈迪剑. 基于带约束S型速度曲线的机械手笛卡尔空间轨迹规划
31、普亚松, 史耀耀, 蔺小军, 张文斌, 陈振. 基于混合多项式插值的工业机器人关节运动规划
32、顾万里, 胡云峰, 宫 洵, 蔡 硕, 陈 虹. 给定速度需求的移动机器人路径跟踪控制与实验
33、Zhijie Li, Ligang Cai, Zhifeng LiuEf. ficient Planning and Solving Algorithm of s-Shape Acceleration and Deceleration
34、朱其新, 陈健亨, 张国平, 刘红俐, 史杰. 一种新型高精度S型加减速控制算法的研究
35、冯剑, 张文安, 倪洪杰, 丰其云. 轮式移动机器人轨迹跟踪的PID控制方法