题意

Copil Copac 给定了一个由 n−1
条边组成的列表，该列表描述了一棵由 n
个顶点组成的树。他决定用下面的算法来绘制它：

步骤 0：绘制第一个顶点（顶点1）。转到步骤1。
步骤 1：对于输入中的每一条边，依次：如果该边连接一个已经制的顶点u和一个未绘制的顶点v ，则绘制未绘制的顶点v 和该边。检查完每一条边后，进入步骤2 。
步骤2 ：如果所有顶点都绘制完毕，则终止算法。否则，转到步 1 。

读取次数定义为 Copil Copac 执行步骤1 的次数。
求出 Copil Copac 画树所需的读数。

输入

输入:
每个测试包含多个测试用例。第一行输入包含一个整数t （1≤t≤104）–测试用例数。测试用例说明如下。
每个测试用例的第一行包含一个整数 n (2≤n≤2⋅105 )–树的顶点数。
每个测试用例的下面n−1 行包含两个整数ui 和vi （1≤ui,vi≤n ui≠vi）–表示(ui,vi) 是列表中的i 条边。可以保证给定的边构成一棵树。
保证所有测试用例的 n 之和不超过 2⋅105

例：
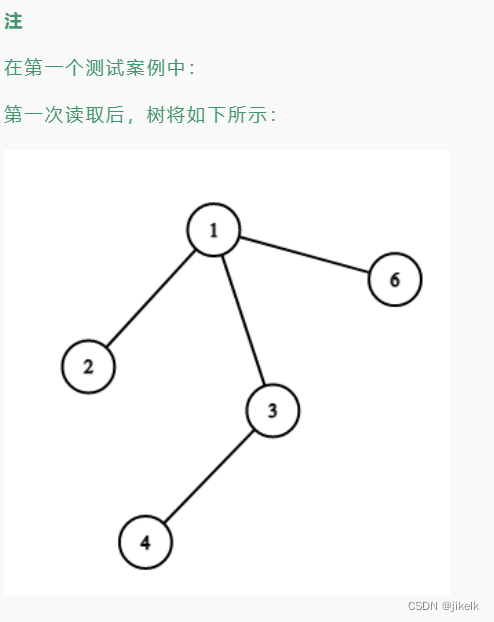
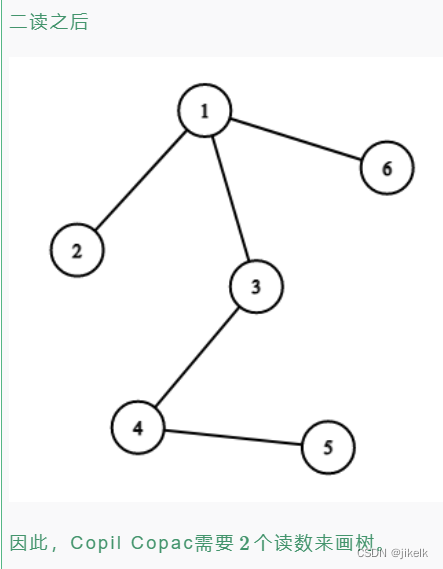
在这里插入图片描述

思路

可以这样思考，对于一个已经构建好了的图的相邻的三个点a,b,c（b点为中间点），如果a,b边构建的序号在b,c,边之后，那么在构建a,b边之后至少还需要一次额外的操作来构建b,c,边。那么可以根据这个思路，从1点开始往他的临界点dfs，判断条件是否需要次数+1，最后所有的值取最大值输出即可。

代码

#include<cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include<vector>
#include<queue>
#include<map>
#define sc_int(x) scanf("%d", &x)
#define sc_ll(x) scanf("%lld", &x)
#define pr_ll(x) printf("%lld", x)
#define pr_ll_n(x) printf("%lld\n", x)
#define pr_int_n(x) printf("%d\n", x)
#define ll long long 
using namespace std;

const int N=1000000+100,inf=0x3f3f3f3f;
int n ,m;
int s[N];

int h[N],ne[N],e[N],idx,w[N];
bool st[N];

map<pair<int,int>,int>q;

void add(int a,int b)//连边
{
    ne[idx]=h[a];
    e[idx]=b;
    h[a]=idx++;
}

int   dfs(int x,int time,int head)
{
    int k=time;
    for(int i =h[x];i!=-1;i=ne[i])
    {
        int j =e[i];
        if(j==head)continue;//如果dfs到上一个节点就不进行dfs
        if(head!=-1&&q[{head,x}]>q[{x,j}]) k =max(k,dfs(j,time+1,x));//dfs遍历
        else k =max(k,dfs(j,time,x));
    }
    return k;
}

void slove( )
{
    int t;
    sc_int(n);
    
    memset(h,-1,sizeof h);
    idx=0;
    for(int i =1;i<n;i++)
    {
        int a,b;
        cin>>a>>b;
        add(a,b),add(b,a);//因为是无向图所以建双向边
        q[{a,b}]=q[{b,a}]=i;//保存次序
    }

    cout<<dfs(1,1,-1);


    cout<<endl;
}

int main()
{
    int t;
    sc_int(t);
    while(t--)
    slove();


    return 0;
}