在上篇我大概介绍了多维数组的地址映射问题,但是不够完善,很多朋友还没有彻底学会,表示很头疼。这一方面的总结确实比较少,而且也很麻烦,但是不要怕,看完我的总结,相信你一定会有一直醍醐灌顶的感觉,这期也将作为上期的一个补充,以三维和四维数组为例,解决实际题目中的问题。
多维数组存储地址计算问题的求解——数据结构_追逐太阳的星星的博客-CSDN博客
上边是关于上篇的一些总结,没有看过的同学可以大概看一下,喜欢的话记得点赞支持哦!
那么废话不多说,我们直接讲干货!
二维数组
我们先来了解一下二维数组的规律
例1.设二维数组A[1...m,1...n](即m行n列)按行存储在数组B[1...m*n]中,则二维数组
素A[i,j]在一维数组B中的下标为( )。【南京理工大学1998 一、2(2分)】
A. (i-1)*n+j
B. (i-1)*n+j-1
C.i*(j-1)
D.j*m+i-1
[解析]:
易得如下结论
行优先存储二维数组素A[i,j]在一维数组B中的下标为:(i-1)*n+j,即:已经存满的行数(i-1)乘以列的总数n,再加上未存满的那一行对应的已经存满的列数j。
列优先存储二维数组素A[i,j]在一维数组B中的下标为:(j-1)*m+i,即:已经存满的列数(j-1)乘以行的总数m,再加上未存满的那一列对应的已经存满的行数i。
三维数组
例2.使用行优先次序存放三维数组A(8,10,20),每个数组元素占4个内存单元,假设数组元素A[0,0,0]的起始存储地址是100,计算数组元素A[7,8,9]的储地址
[解析]:
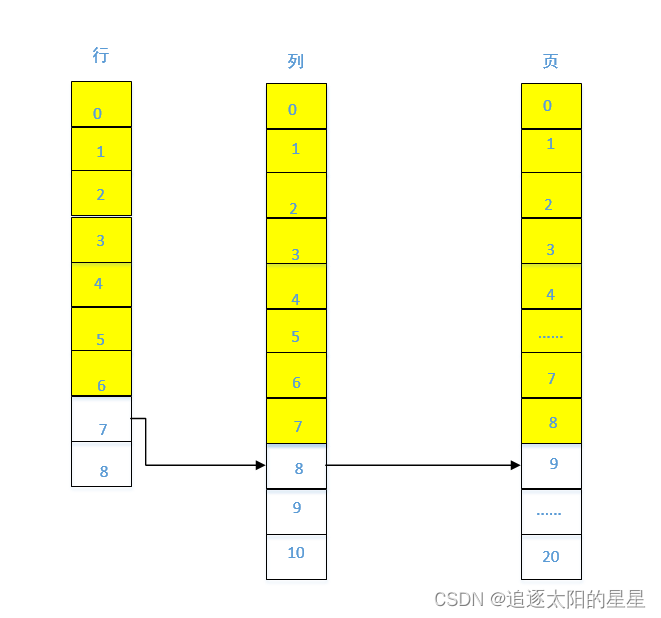
如图所示,表示的是三维数组的存储结构,黄色区域代表满,三维数组的前7行均满,存了7×10×20=1400个元素,三维数组第8行存满了8个二维数组、9个一维数组(此处未包含下标为9处的元素),对应的元素个数分别为:8×20=160、9,共计1400+160+9=1569个元素,每个元素占4个存储单元,1569×4=6276,又因为起始位置为100,6276+100=6376,故本题答案为6376。
例3.三维数组a[4][5][6](下标从0开始计,a有4*5*6个元素)中每个元素的长度是2,则a[2][3][4]的地址是______。(设a[0][0][0]的地址是1000,数据以行为主方式存储。)【南京理工大学2000二、11(1.5分)】
[解析]:(2×5×6+3×6+4)×2+1000=1164,本题答案为1164。
例4.数组A[1...10,-2...6,2...8] 以列优先的顺序存储,设第一个元素的首地址是100,每个元素占3个存储长度的存储空间,则元素A[5,0,7]的存储地址为_____。
注意:按列存储与按行存储稍有不同,按行存储为行、列、页的顺序计算,而按列存储需要按照页、列、行的顺序来计算,两者刚好相反,2维、3维、4维均适用。
[解析]: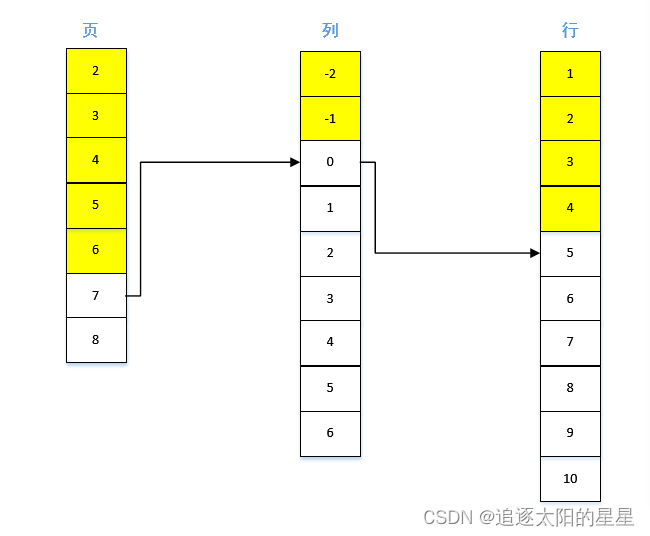
(6×9×10+2×10+4)×3+100=1522,本题答案为1522。
四维数组
例5.设四维数组B=[1...3,2...8,1...5,1...8],每个数据元素占一个存储单元,且行优先存储时B[1,2,2,3]的存储地址为2000,分别计算出B[2,4,4,6]按行优先存储和按列优先存储的存储地址。
[解析]:
先计算初始地址:2000-(8+3)=1989
按行优先存储:(1×7×5×8+2×5×8+3×8+6)+1989=2379
按列优先存储:(5×5×7×3+3×7×3+2×3+2)+1989=2585
以上是我的个人总结,如有错误,望大家指正!如果对你有帮助的话记得点赞呦,另外如果大家有数据结构方面不会的可以私信我,我不忙的时候会写文章给大家解答的!谢谢大家支持!