原文链接：http://tecdat.cn/?p=12280
马尔可夫链是从一个“状态”（一种情况或一组值）跳到另一个“状态”的数学系统。本文介绍了马尔可夫链和一种简单的状态转移模型，该模型构成了隐马尔可夫模型（HMM）的特例。从应用的角度来看，这些模型在评估经济/市场状态数据时（查看文末了解数据获取方式）非常有用。这里的讨论主要围绕使用这些模型的科学性。
（点击文末“阅读原文”获取完整代码数据）。
视频：马尔可夫链原理可视化解释与R语言区制转换Markov regime switching实例
例如，如果您制作了婴儿行为的马尔可夫链模型，您可能会将“玩耍”、“吃饭”、“睡觉”和“哭泣”作为状态，它们与其他行为一起可以形成“状态空间”：所有可能状态的列表。此外，在状态空间之上，马尔可夫链告诉您从一个状态跳跃或“转换”到任何其他状态的概率——例如，正在玩耍的婴儿在下一个状态下入睡的可能性五分钟不先哭。
一个简单的两态马尔可夫链如下所示。
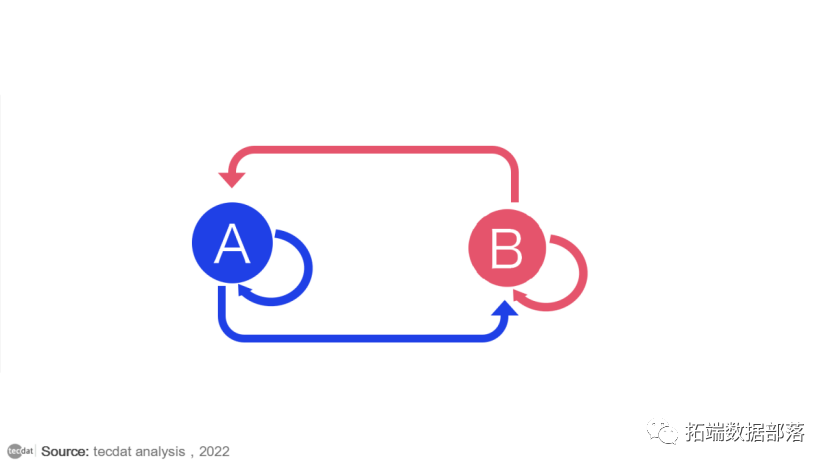
在我们的状态空间中有两种状态（A 和 B），有 4 种可能的转换（不是 2 种，因为状态可以转换回自身）。如果我们在“A”，我们可以过渡到“B”或留在“A”。如果我们在“B”，我们可以过渡到“A”或留在“B”。在这两个状态图中，从任何状态转换到任何其他状态的概率为 0.5。
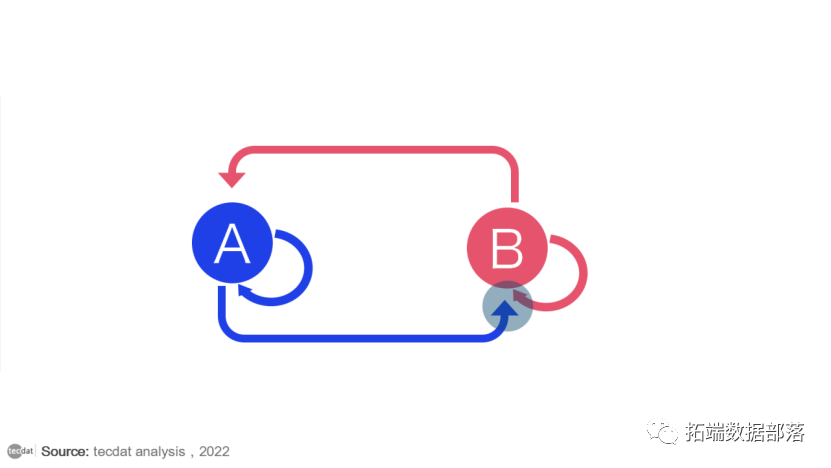
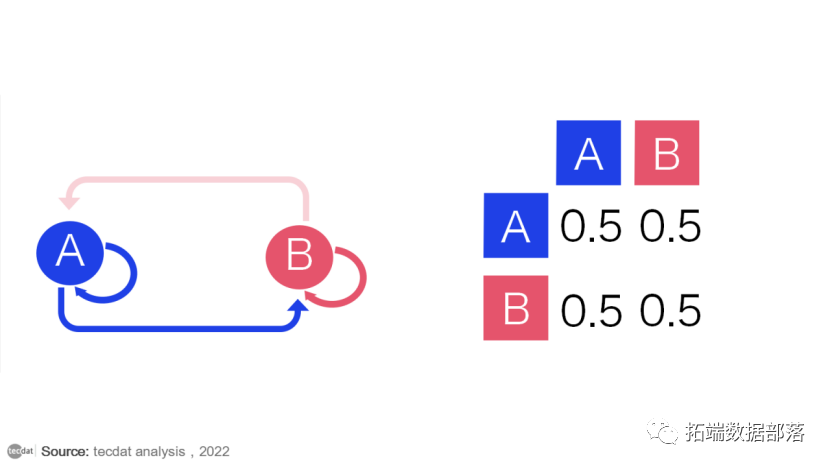
当然，真正的建模者并不总是画出马尔可夫链图。相反，他们使用“转移矩阵”来计算转移概率。状态空间中的每个状态都包含一次作为行和列，并且矩阵中的每个单元格都告诉您从其行状态转换到其列状态的概率。因此，在矩阵中，单元格的作用与图中箭头的作用相同。
如果状态空间添加一个状态，我们添加一行和一列，每个现有的列和行添加一个单元格。这意味着当我们向马尔可夫链添加状态时，单元格的数量呈二次增长。因此，除非您想绘制丛林健身房马尔可夫链图，否则转换矩阵很快就会派上用场。
马尔可夫链的一种用途是在计算机模拟中包含真实世界的现象。例如，我们可能想要检查新大坝的溢出频率，这取决于连续下雨的天数。为了建立这个模型，我们从以下雨天 (R) 和晴天 (S) 开始：
模拟这种天气的一种方法是只说“有一半的日子下雨。因此，在我们的模拟中，每天都有 50% 的几率下雨。”
该规则将在模拟中生成以下序列：
你有没有注意到上面的序列看起来和原来的不太一样？第二个序列似乎跳来跳去，而第一个（真实数据）似乎具有“粘性”。在实际数据中，如果一天是晴天（S），那么第二天晴天的可能性也更大。
我们可以使用两态马尔可夫链来缩小这种“粘性”。当马尔可夫链处于“R”状态时，它有 0.9 的概率留在原地，有 0.1 的机会离开“S”状态。同样，“S”状态有 0.9 的概率保持原状，并且有 0.1 的机会转换到“R”状态。
在气象学家、生态学家、计算机科学家、金融工程师和其他需要对大现象建模的人群中，马尔可夫链可以变得非常庞大和强大。例如，谷歌用来确定搜索结果顺序的算法，称为PageRank，是一种马尔可夫链。
马尔可夫区制转移模型Markov regime switching
本文简要介绍了一种简单的状态转移模型，该模型构成了隐马尔可夫模型（HMM）的特例。这些模型拟合时间序列数据中的非平稳性。
基本案例
HMM的主要挑战是预测隐藏部分。我们如何识别“不可观察”的事物？HMM的想法是从可观察的事物来预测潜在的事物。
模拟数据
为了演示，我们准备一些数据并尝试进行反向推测。每个状态都具有不同的均值和波动率。
theta_v <- data.frame(t(c(2.00,-2.00,1.00,2.00,0.95,0.85)))
kable(theta_v, "html", booktabs = F,escape = F) %>%
kable_styling(position = "center")
如上表所示，状态s = 2变成“坏”状态，其中过程x_t表现出较高的变化性。因此，停留在状态2的可能比停留在状态1的可能性小。
马尔可夫过程
为了模拟过程x\_t ，我们从模拟马尔可夫过程s\_t 开始。为了模拟T 期间的过程，首先，我们需要构建给定p_ {11} 和p_ {22} 的转换矩阵。其次，我们需要从给定状态s\_1 = 1 开始。从s\_1 = 1 开始，我们知道有95％的概率停留在状态1，有5％的概率进入状态2。
P <- matrix(c(p11,1-p22,1-p11,p22),2,2)
P\[1,\]## \[1\] 0.95 0.05因为它先前的状态，模拟s_t 是递归的。因此，我们需要构造一个循环：
for(t in 2:T_end) {
s <- c(s,st(s\[t-1\]))
}
plot(s, pch = 20,cex = 0.5)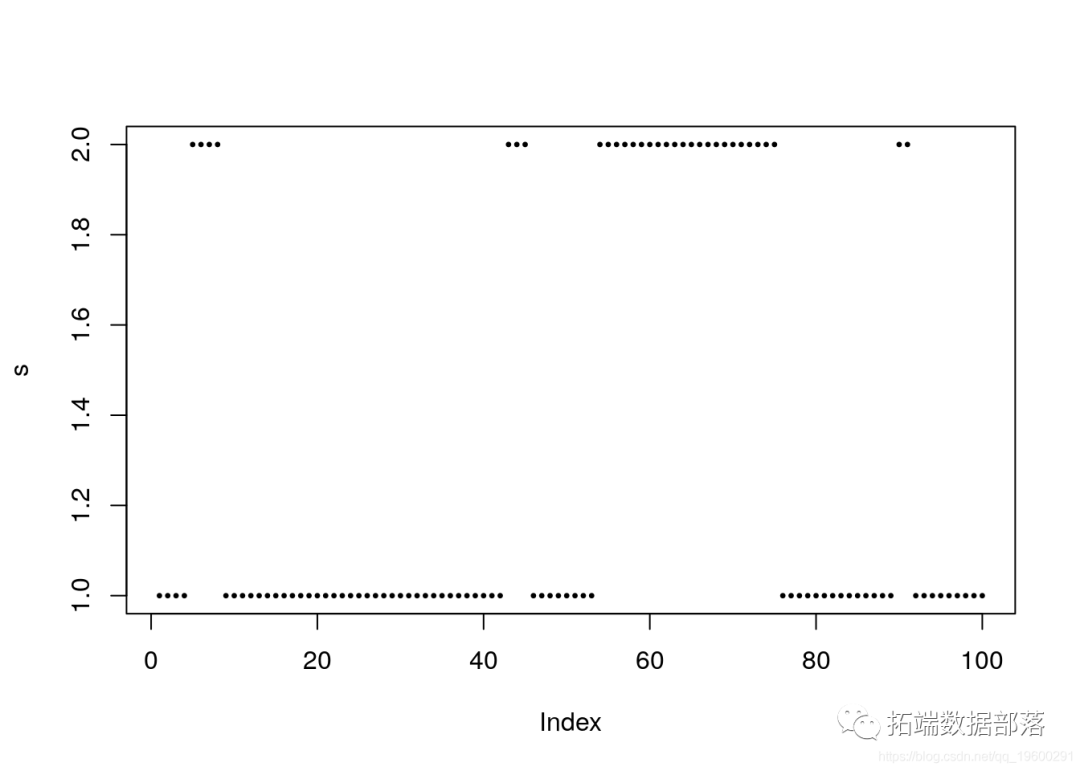
上图说明了过程s_t的持久性。在大多数情况下，状态1的“实现”多于状态2。实际上，这可以由稳定概率确定，该稳定概率由下式表示：
P_stat\[1,\]## \[1\] 0.75 0.25因此，有15％的概率处于1状态，而有25％的概率处于状态2。这应该反映在模拟过程中 s，从而
mean(s==1)## \[1\] 0.69由于我们使用的是100个周期的小样本，因此我们观察到稳定概率为69％，接近但不完全等于75％。
结果
给定模拟的马尔可夫过程，结果的模拟非常简单。一个简单的技巧是模拟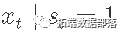
的T周期和
的 T 周期。然后，给定 s\_t 的模拟，我们针对每个状态创建结果变量 x\_t 。
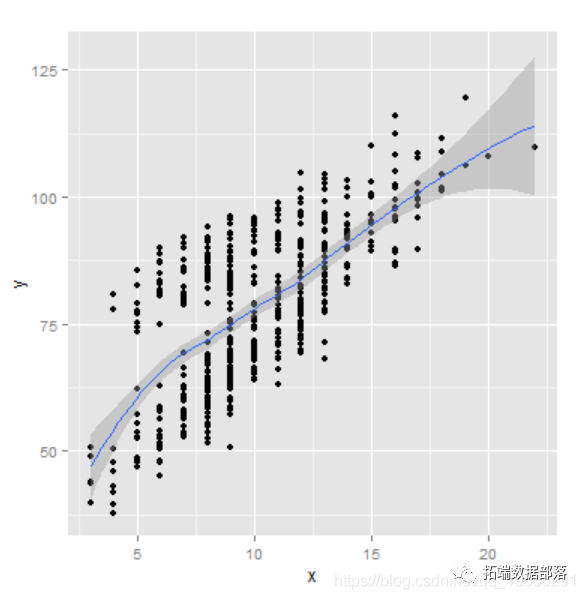
plot(x~t_index, pch = 20)
points(x\[s == 2\]~t_index\[s==2\],col = 2)
点击标题查阅往期内容
R语言如何做马尔可夫转换模型markov switching model
左右滑动查看更多
01
02
03
04
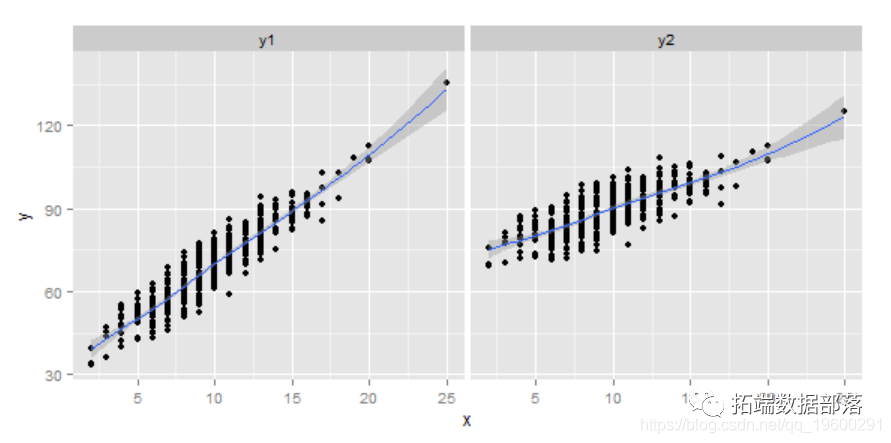
虽然总体而言时间序列看起来是平稳的，但我们观察到一些周期（以红色突出显示）显示出较高的波动。有人可能会建议说，数据存在结构性中断，或者区制发生了变化，过程 x_t 变得越来越大，带有更多的负值。虽然如此，事后解释总是比较容易的。主要的挑战是识别这种情况。
估计参数
在本节中，我将使用R软件手动（从头开始）和非手动进行统计分解。在前者中，我将演示如何构造似然函数，然后使用约束优化问题来估计参数。
似然函数-数值部分
首先，我们需要创建一个以 Theta 向量为主要输入的函数。其次，我们需要设置一个MLE的优化问题。
在优化似然函数之前。让我们看一下工作原理。假设我们知道参数 Theta 的向量，并且我们有兴趣使用 x_t 上的数据评估随时间变化的隐藏状态。
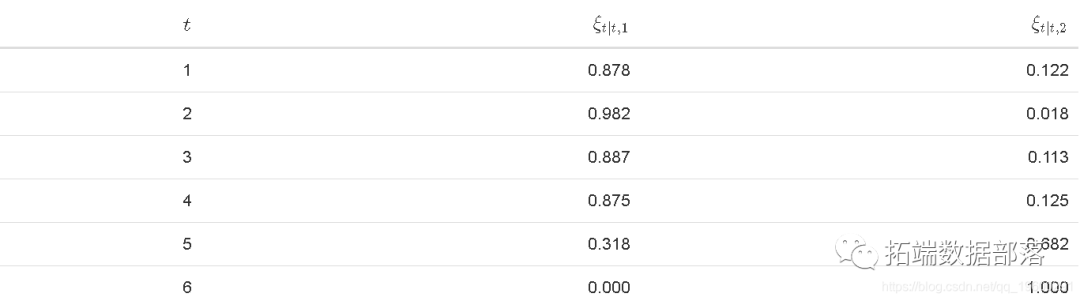
显然，这两种状态的每次过滤器的总和应为1。看起来，我们可以处于状态1或状态2。
all(round(apply(Filter\[,-1\],1,sum),9) == 1)## \[1\] TRUE由于我们设计了此数据，因此我们知道状态2的时期。
plot(Filter\[,3\]~t_index, type = "l", ylab = expression(xi\[2\]))
points(Filter\[s==2,3\]~t_index\[s==2\],pch = 20, col = 2)
过滤器背后的优点是仅使用 x_t 上的信息来识别潜在状态。我们观察到，状态2的过滤器主要在状态2发生时增加。这可以通过发出红点的概率增加来证明，红点表示状态2发生的时间段。尽管如此，上述还是存在一些大问题。首先，它假定我们知道参数 Theta ，而实际上我们需要对此进行估计，然后在此基础上进行推断。其次，所有这些都是在样本中构造的。从实际的角度来看，决策者对预测的概率及其对未来投资的影响感兴趣。
手动估算
为了优化上面定义的 HMM_Lik 函数，我将需要执行两个附加步骤。首先是建立一个初始估计值，作为搜索算法的起点。其次，我们需要设置约束条件以验证估计的参数是否一致，即非负波动性和介于0和1之间的概率值。
第一步，我使用样本创建初始参数向量Theta_0
在第二步中，我为估算设置了约束
请注意，参数的初始向量应满足约束条件
all(A%*%theta0 >= B)## \[1\] TRUE最后，回想一下，通过构建大多数优化算法都可以搜索最小点。因此，我们需要将似然函数的输出更改为负值。
## $par
## \[1\] 1.7119528 -1.9981224 0.8345350 2.2183230 0.9365507 0.8487511
##
## $value
## \[1\] 174.7445
##
## $counts
## function gradient
## 1002 NA
##
## $convergence
## \[1\] 0
##
## $message
## NULL
##
## $outer.iterations
## \[1\] 3
##
## $barrier.value
## \[1\] 6.538295e-05为了检查MLE值是否与真实参数一致，我们绘制估计值与真实值的关系图：
plot(opt$par ~ theta_known,pch = 20,cex=2,ylab="MLE",xlab = "True")
abline(a=0,b=1,lty=2)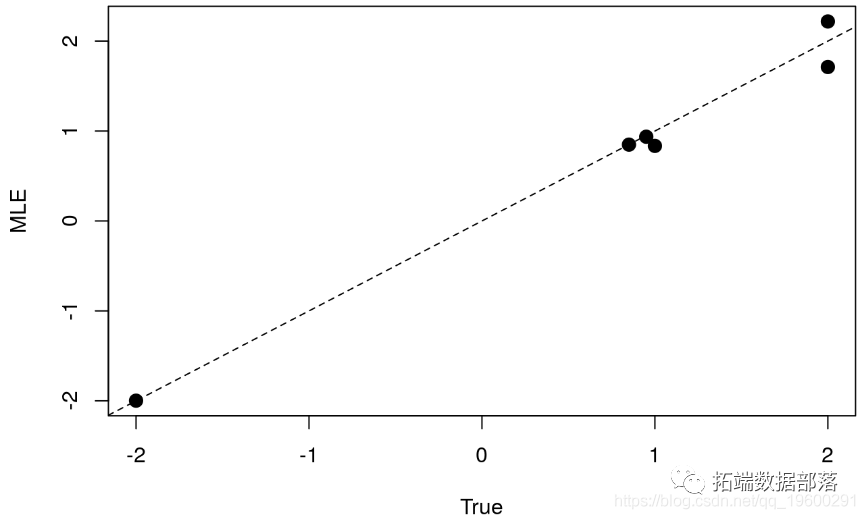
总体而言，我们观察到估计值非常一致。
估算
我将在下面演示如何使用r软件复制人工估算的结果 。
如果我们要忽略过程中的任何区制转换，我们可以简单地将参数 mu 和 sigma 估计为
kable(mod_est, "html", booktabs = F,escape = F) %>%
kable_styling(position = "center")
平均而言，我们应该期望过程平均值约为1，即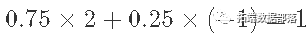
。这是由期望定律得出的，其中我们知道
EX <- 0.75\*2 + 0.25\*-2
EX## \[1\] 1对于波动率，适用相同的逻辑。
## \[1\] 2.179449我们注意到，回归估计值与波动率的一致性高于均值。
上面的观点是，估计值并未涵盖数据的真实性质。如果我们假设数据是稳定的，那么我们错误地估计过程的平均值为62％。但是，与此同时，我们通过构造知道该过程表现出两个平均结果-一个正面和一个负面。波动性也是如此。
为了揭示这些模式，我们在下面演示如何使用上面的线性模型建立区制转移模型：
主要输入是拟合模型， mod我们将其归纳为拟合转移状态。第二个 k是区制的数量。由于我们知道我们要处理两个状态，因此将其设置为2。但是，实际上，需要参考一种信息标准来确定最佳状态数。根据定义，我们有两个参数，均值 mu\_s 和波动率 sigma\_s 。因此，我们添加一个true / false向量来指示正在转移的参数。在上面的命令中，我们允许两个参数都转移。最后，我们可以指定估计过程是否正在使用并行计算进行。
要了解模型的输出，让我们看一下
## Markov Switching Model
##
##
## AIC BIC logLik
## 352.2843 366.705 -174.1422
##
## Coefficients:
## (Intercept)(S) Std(S)
## Model 1 1.711693 0.8346013
## Model 2 -2.004137 2.2155742
##
## Transition probabilities:
## Regime 1 Regime 2
## Regime 1 0.93767719 0.1510052
## Regime 2 0.06232281 0.8489948上面的输出主要报告我们尝试手动估算的六个估算参数。首先，系数表报告了每个状态的均值和波动。模型1的平均值为1.71，波动率接近1。模型2的平均值为-2，波动率约为2。显然，该模型针对数据确定了两种具有不同均值和波动率的不同状态。其次，在输出的底部，拟合的模型报告了转移概率。
有趣的是，就每种状态的过滤器而言，我们将从包中检索到的状态与手动提取的状态进行比较。根据定义，可以使用图函数 来了解平滑概率以及确定的方案。
par(mar = 2*c(1,1,1,1),mfrow = c(2,1))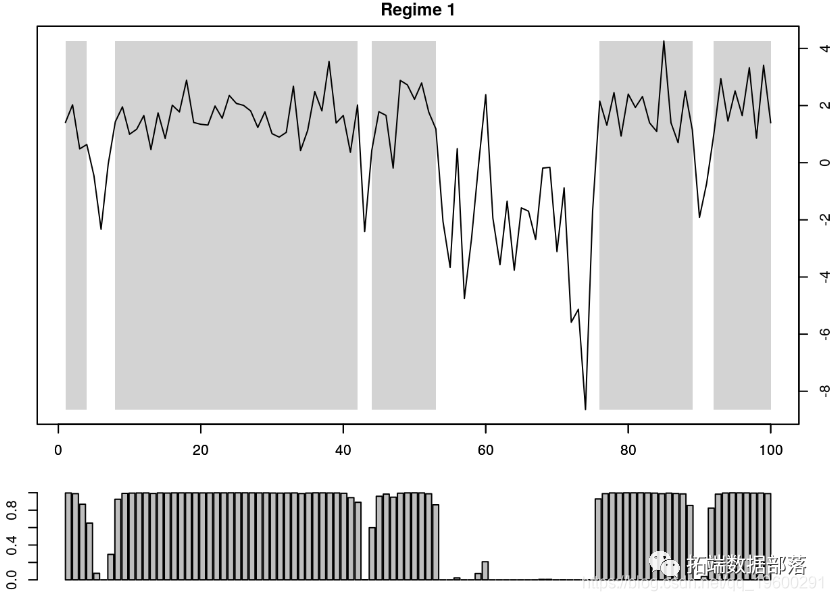
顶部的图表示随时间变化的过程 x_t ，其中灰色阴影区域表示
的时间段。换句话说，灰色区域表示状态1占优势的时间段。
plot(x~t_index,type ="l",col = 0,xlim=c(1,100))
过滤器会在一个周期内检测到第二种状态。发生这种情况是因为在这种情况下，返回的是平滑概率，即在实现整个样本 T 后处于每种状态的概率，即
。另一方面，来自手动估计的推断概率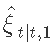
。
无论如何，由于我们知道状态的真实值，因此可以确定我们是否处于真实状态。我们在上面的图中使用黑点突出显示状态2。总的来说，我们观察到模型在检测数据状态方面表现非常好。唯一的例外是第60天，其中推断概率大于50％。要查看推断概率多长时间正确一次，我们运行以下命令
mean(Filter$Regime_1 == (s==1)*1)## \[1\] 0.96结束语
在实际数据实现方面仍然存在许多挑战。首先，我们不具备有关数据生成过程的知识。其次，状态不一定实现。因此，这两个问题可能会破坏区制转移模型的可靠性。在应用方面，通常部署此类模型来评估经济或市场状况。从决策上来说，这也可以为策略分配提供有趣的建议。
数据获取
在下面公众号后台回复“MRS数据”，可获取完整数据。
本文中分析的数据分享到会员群，扫描下面二维码即可加群！
本文摘选《R语言马尔可夫区制转移模型Markov regime switching》，点击“阅读原文”获取全文完整资料。
点击标题查阅往期内容
时变马尔可夫区制转换MRS自回归模型分析经济时间序列
马尔可夫转换模型研究交通伤亡人数事故时间序列预测
如何实现马尔可夫链蒙特卡罗MCMC模型、Metropolis算法？
Matlab用BUGS马尔可夫区制转换Markov switching随机波动率模型、序列蒙特卡罗SMC、M H采样分析时间序列
matlab用马尔可夫链蒙特卡罗 (MCMC) 的Logistic逻辑回归模型分析汽车实验数据
R语言BUGS序列蒙特卡罗SMC、马尔可夫转换随机波动率SV模型、粒子滤波、Metropolis Hasting采样时间序列分析
stata马尔可夫Markov区制转移模型分析基金利率
PYTHON用时变马尔可夫区制转换（MRS）自回归模型分析经济时间序列
R语言使用马尔可夫链对营销中的渠道归因建模
matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计
R语言隐马尔可夫模型HMM识别不断变化的股票市场条件
R语言中的隐马尔可夫HMM模型实例
用机器学习识别不断变化的股市状况—隐马尔科夫模型(HMM)
Matlab马尔可夫链蒙特卡罗法（MCMC）估计随机波动率（SV，Stochastic Volatility） 模型
MATLAB中的马尔可夫区制转移(Markov regime switching)模型
Matlab马尔可夫区制转换动态回归模型估计GDP增长率
R语言马尔可夫区制转移模型Markov regime switching
stata马尔可夫Markov区制转移模型分析基金利率
R语言如何做马尔可夫转换模型markov switching model
R语言隐马尔可夫模型HMM识别股市变化分析报告
R语言中实现马尔可夫链蒙特卡罗MCMC模型
