目录
103. 二叉树的锯齿形层次遍历
236. 二叉树的最近公共祖先
124. 二叉树中的最大路径和
102. 二叉树的层序遍历
94. 二叉树的中序遍历
110. 平衡二叉树
572. 另一个树的子树
96. 不同的二叉搜索树
543. 二叉树的直径
297. 二叉树的序列化与反序列化
199. 二叉树的右视图
105. 从前序与中序遍历序列构造二叉树
113. 路径总和 II
337. 打家劫舍 III
662. 二叉树最大宽度
104. 二叉树的最大深度
98. 验证二叉搜索树
101. 对称二叉树
144. 二叉树的前序遍历
1339. 分裂二叉树的最大乘积
450. 删除二叉搜索树中的节点
145. 二叉树的后序遍历
112. 路径总和
剑指 Offer 34. 二叉树中和为某一值的路径
129. 求根到叶子节点数字之和
226. 翻转二叉树
652. 寻找重复的子树
222. 完全二叉树的节点个数
257. 二叉树的所有路径
剑指 Offer 32 - III. 从上到下打印二叉树 III
剑指 Offer 07. 重建二叉树
剑指 Offer 54. 二叉搜索树的第k大节点
103. 二叉树的锯齿形层次遍历
# 103. 二叉树的锯齿形层序遍历
# 给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
# 输入:root = [3,9,20,null,null,15,7]
# 输出:[[3],[20,9],[15,7]]
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
from typing import List
class Solution:
def zigzagLevelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
ans=[]
q=[root]
level=0
while len(q)>0:
level_len=len(q)
t=[]
print(level_len,q)
for i in range(level_len):
cur=q[0]
q.pop(0)
if(cur):
t.append(cur.val)
if cur.left:
q.append(cur.left)
if cur.right:
q.append(cur.right)
if level%2==1:
t=t[::-1]
ans.append(t)
level+=1
return ans236. 二叉树的最近公共祖先

# 236. 二叉树的最近公共祖先
# 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
# 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
self.ans=None
def dfs(root,p,q):
if not root:
return False
l=dfs(root.left,p,q)
r=dfs(root.right,p,q)
if(l and r) or ((root.val==p.val or root.val==q.val) and (l or r)):
self.ans=root
return (root.val==p.val or root.val==q.val) or l or r
dfs(root,p,q)
return self.ans124. 二叉树中的最大路径和
# 124. 二叉树中的最大路径和
# 路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
# 路径和 是路径中各节点值的总和。
# 给你一个二叉树的根节点 root ,返回其 最大路径和 。
#
# 输入:root = [1,2,3]
# 输出:6
# 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxPathSum(self, root: Optional[TreeNode]) -> int:
self.total=float('-inf')
def dfs(root):
if not root:
return 0
res_l=max(dfs(root.left),0)
res_r=max(dfs(root.right),0)
local_total=res_r+res_l+root.val
self.total=max(local_total,self.total)
return root.val+max(res_l,res_r)
dfs(root)
return self.total
'''
class Solution:
def __init__(self):
self.maxSum = float("-inf")
def maxPathSum(self, root: TreeNode) -> int:
def maxGain(node):
if not node:
return 0
# 递归计算左右子节点的最大贡献值
# 只有在最大贡献值大于 0 时,才会选取对应子节点
leftGain = max(maxGain(node.left), 0)
rightGain = max(maxGain(node.right), 0)
# 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
priceNewpath = node.val + leftGain + rightGain
# 更新答案
self.maxSum = max(self.maxSum, priceNewpath)
# 返回节点的最大贡献值
return node.val + max(leftGain, rightGain)
maxGain(root)
return self.maxSum
'''102. 二叉树的层序遍历
# 102. 二叉树的层序遍历
# 给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
# 输入:root = [3,9,20,null,null,15,7]
# 输出:[[3],[9,20],[15,7]]
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
q=[root]
ans=[]
while q:
level_len=len(q)
t = []
for i in range(level_len):
cur=q[0]
q.pop(0)
if cur:
t.append(cur.val)
if cur.left:
q.append(cur.left)
if cur.right:
q.append(cur.right)
ans.append(t)
return ans94. 二叉树的中序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
# 递归
# class Solution:
# def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
# if root is None:
# return []
# return self.inorderTraversal(root.left)+[root.val]+self.inorderTraversal(root.right)
# 非递归
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
q=[]
res=[]
cur=root
while cur or q:
while cur:
q.append(cur)
cur=cur.left
cur=q.pop()
res.append(cur.val)
cur=cur.right
return res110. 平衡二叉树
# 110. 平衡二叉树
# 给定一个二叉树,判断它是否是高度平衡的二叉树。
#
# 本题中,一棵高度平衡二叉树定义为:
# 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
def get_high(a):
if a==None:
return 0
return max(get_high(a.left),get_high(a.right))+1
if root==None:
return True
if(abs(get_high(root.left)-get_high(root.right))>1):
return False
return self.isBalanced(root.left) and self.isBalanced(root.right)572. 另一个树的子树
# 572. 另一棵树的子树
# 给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
#
# 二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
# [3,4,5,1,2] true
# [4,1,2]
# class Solution {
# public:
# bool check(TreeNode *o, TreeNode *t) {
# if (!o && !t) {
# return true;
# }
# if ((o && !t) || (!o && t) || (o->val != t->val)) {
# return false;
# }
# return check(o->left, t->left) && check(o->right, t->right);
# }
#
# bool dfs(TreeNode *o, TreeNode *t) {
# if (!o) {
# return false;
# }
# return check(o, t) || dfs(o->left, t) || dfs(o->right, t);
# }
#
# bool isSubtree(TreeNode *s, TreeNode *t) {
# return dfs(s, t);
# }
# };
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSubtree(self, root: TreeNode, subRoot: TreeNode) -> bool:
def isSame(a,b):
if not a and not b:
return True
if (not a and b) or (a and not b) or (a.val!=b.val):
return False
return isSame(a.left,b.left) and isSame(a.right,b.right)
if (root==None) :
return False
return isSame(root,subRoot) or self.isSubtree(root.left,subRoot) or self.isSubtree(root.right,subRoot)96. 不同的二叉搜索树
# 96. 不同的二叉搜索树
# 给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
# dp[j] dp[j-1]*dp[i-j] 我们选择数字 j作为根,则根为j的所有二叉搜索树的集合是左子树集合和右子树集合乘积
class Solution:
def numTrees(self, n: int) -> int:
dp=[0]*(n+1)
dp[0]=1
dp[1]=1
for i in range(2,n+1):
for j in range(i+1):
dp[i]+=dp[j-1]*dp[i-j]
print(dp)
return dp[n]
n=10
s=Solution()
r=s.numTrees(n)
print(r)543. 二叉树的直径
# 543. 二叉树的直径
# 给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
# 返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
self.diameter=0
def dfs(root):
if root==None:
return 0
high_l=dfs(root.left)
high_r=dfs(root.right)
local_diameter=high_r+high_l+1
# print(high_l,high_r,local_diameter,max(high_l,high_r)+1)
self.diameter=max(local_diameter,self.diameter)
return max(high_l,high_r)+1
dfs(root)
return self.diameter-1297. 二叉树的序列化与反序列化
# 297. 二叉树的序列化与反序列化
# 序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据。
#
# 请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑,你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
#
# 提示: 输入输出格式与 LeetCode 目前使用的方式一致,详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式,你也可以采用其他的方法解决这个问题。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Codec:
def serialize(self, root):
"""Encodes a tree to a single string.
:type root: TreeNode
:rtype: str
"""
if not root:
return 'None' #相等于满二叉树了
return str(root.val)+','+self.serialize(root.left)+','+self.serialize(root.right)
def deserialize(self, data):
"""Decodes your encoded data to tree.
:type data: str
:rtype: TreeNode
"""
def dfs(arr):
if arr[0]=='None':
arr.pop(0)
return None
val=arr[0]
arr.pop(0)
root=TreeNode(val)
root.left=dfs(arr)
root.right=dfs(arr)
return root
data_arr=data.split(',')
root=dfs(data_arr)
return root
# Your Codec object will be instantiated and called as such:
# ser = Codec()
# deser = Codec()
# ans = deser.deserialize(ser.serialize(root))199. 二叉树的右视图
# 199. 二叉树的右视图
# 给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
# 输入: [1,2,3,null,5,null,4]
# 输出: [1,3,4]
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
from typing import List
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
res=[]
q=[root]
while len(q)>0:
level_len=len(q)
for i in range(level_len):
cur = q[0]
q.pop(0)
if cur:
if i == level_len - 1:
res.append(cur.val)
if cur.left:
q.append(cur.left)
if cur.right:
q.append(cur.right)
return res
# class Solution:
# def rightSideView(self, root: TreeNode) -> List[int]:
# rightmost_value_at_depth = dict() # 深度为索引,存放节点的值
# max_depth = -1
#
# stack = [(root, 0)]
# while stack:
# node, depth = stack.pop()
#
# if node is not None:
# # 维护二叉树的最大深度
# max_depth = max(max_depth, depth)
#
# # 如果不存在对应深度的节点我们才插入
# rightmost_value_at_depth.setdefault(depth, node.val)
#
# stack.append((node.left, depth + 1))
# stack.append((node.right, depth + 1))
#
# return [rightmost_value_at_depth[depth] for depth in range(max_depth + 1)]
105. 从前序与中序遍历序列构造二叉树
# 105. 从前序与中序遍历序列构造二叉树
# 给定两个整数数组preorder 和 inorder,其中preorder 是二叉树的先序遍历, inorder是同一棵树的中序遍历,请构造二叉树并返回其根节点。
#
# 输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
# 输出: [3,9,20,null,null,15,7]
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
# def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
def buildTree(self, preorder, inorder):
if not preorder and not inorder:
return None
val=preorder[0]
val_i=inorder.index(val)
root=TreeNode(val)
root.left=self.buildTree(preorder[1:val_i+1],inorder[0:val_i])
root.right=self.buildTree(preorder[val_i+1:],inorder[val_i+1:])
return root113. 路径总和 II
# 113. 路径总和 II
# 给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
#
# 叶子节点 是指没有子节点的节点。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
ans = []
def dfs(root, target, path):
if root == None:
return
if root.left == None and root.right == None:
path.append(root.val)
if target - root.val == 0:
ans.append(path[::])
return
dfs(root.left, target - root.val, path + [root.val])
dfs(root.right, target - root.val, path + [root.val])
dfs(root, targetSum, [])
return ans
337. 打家劫舍 III
# 337. 打家劫舍 III
# 小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为root。
#
# 除了root之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
#
# 给定二叉树的root。返回在不触动警报的情况下,小偷能够盗取的最高金额。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rob(self, root: Optional[TreeNode]) -> int:
if root ==None:
return 0
def dfs(root):
if root==None:
return [0,0]
left_val=dfs(root.left)
right_val=dfs(root.right)
rob_0=max(left_val[0],left_val[1])+max(right_val[0],right_val[1])
rob_1=left_val[0]+right_val[0]+root.val
return [rob_0,rob_1]
return max(dfs(root))662. 二叉树最大宽度
# 662. 二叉树最大宽度
# 给你一棵二叉树的根节点 root ,返回树的 最大宽度 。
#
# 树的 最大宽度 是所有层中最大的 宽度 。
#
# 每一层的 宽度 被定义为该层最左和最右的非空节点(即,两个端点)之间的长度。将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度。
#
# 题目数据保证答案将会在 32 位 带符号整数范围内。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:
q=[[root,1]]
global_wide=1
while q:
t = []
for cur,i in q:
if(cur.left):
t.append([cur.left,i*2])
if(cur.right):
t.append([cur.right, i*2+1])
local_wide = q[-1][1] - q[0][1]+1
q = t
global_wide=max(global_wide,local_wide)
return global_wide104. 二叉树的最大深度
# 104. 二叉树的最大深度
# 给定一个二叉树,找出其最大深度。
#
# 二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
#
# 说明: 叶子节点是指没有子节点的节点。
#
# 示例:
# 给定二叉树 [3,9,20,null,null,15,7],返回它的最大深度 3 。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
return max(self.maxDepth(root.left),self.maxDepth(root.right))+198. 验证二叉搜索树
# 98. 验证二叉搜索树
# 给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
#
# 有效 二叉搜索树定义如下:
#
# 节点的左子树只包含 小于 当前节点的数。
# 节点的右子树只包含 大于 当前节点的数。
# 所有左子树和右子树自身必须也是二叉搜索树。
#
# 输入:root = [2,1,3]
# 输出:true
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
if root == None:
return True
self.pre = float('-inf')
def dfs(root):
if root == None:
return True
left_ = dfs(root.left)
# print(self.pre,root)
if (self.pre >= root.val):
return False
self.pre = root.val
right_ = dfs(root.right)
return left_ and right_
return dfs(root)101. 对称二叉树
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
if root==None:
return True
def dfs(a,b):
if(a==None and b==None):
return True
if(a!=None and b==None) or(a==None and b!=None) or (a.val!=b.val):
return False
left_t=dfs(a.left,b.right)
right_t=dfs(a.right,b.left)
return left_t and right_t
return dfs(root.left,root.right)
144. 二叉树的前序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if root==None:
return []
return [root.val]+self.preorderTraversal(root.left)+self.preorderTraversal(root.right)1339. 分裂二叉树的最大乘积
# 1339. 分裂二叉树的最大乘积
# 给你一棵二叉树,它的根为root 。请你删除 1 条边,使二叉树分裂成两棵子树,且它们子树和的乘积尽可能大。
#
# 由于答案可能会很大,请你将结果对 10^9 + 7 取模后再返回。
# 输入:root = [1,2,3,4,5,6]
# 输出:110
# 解释:删除红色的边,得到 2 棵子树,和分别为 11 和 10 。它们的乘积是 110 (11*10)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxProduct(self, root: Optional[TreeNode]) -> int:
def dfs(r):
if r is None:
return 0
return dfs(r.left)+dfs(r.right)+r.val
allSum=dfs(root)
ans = 0
print("allSum",allSum)
def dfs2(r):
nonlocal allSum
nonlocal ans
if r is None:
return 0
left_val=dfs2(r.left)
right_val=dfs2(r.right)
cur_sum=left_val+right_val+r.val
ans=max((allSum-cur_sum)*cur_sum,ans)
return cur_sum
dfs2(root)
return int(ans%(1e9 + 7))450. 删除二叉搜索树中的节点
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
# class Solution {
# public TreeNode deleteNode(TreeNode root, int key) {
# if (root == null) return null;
# if (root.val == key) {
# if (root.left == null) return root.right;
# if (root.right == null) return root.left;
# TreeNode t = root.left;
# while (t.right != null) t = t.right;
# t.right = root.right;
# return root.left;
# } else if (root.val < key) root.right = deleteNode(root.right, key);
# else root.left = deleteNode(root.left, key);
# return root;
# }
# }
class Solution:
def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
if root == None:
return None
if(root.val==key):
if root.left==None:
return root.right
if root.right==None:
return root.left
t=root.left #最左右子树
while t.right:
t=t.right
t.right=root.right
return root.left
elif(root.val<key):
root.right=self.deleteNode(root.right,key)
else:
root.left=self.deleteNode(root.left,key)
return root145. 二叉树的后序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if root==None:
return []
return self.postorderTraversal(root.left)+self.postorderTraversal(root.right)+[root.val]112. 路径总和
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
if root==None:
return False
def dfs(root,target):
if root==None:
return False
if root.right==None and root.left==None:
if(target==root.val):
return True
return False
left_t=dfs(root.left,target-root.val)
right_t=dfs(root.right,target-root.val)
return left_t or right_t
return dfs(root,targetSum)
剑指 Offer 34. 二叉树中和为某一值的路径
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def pathSum(self, root: TreeNode, target: int) -> List[List[int]]:
if root==None:
return []
def dfs(root,target,path):
if root==None:
return []
if root.left==None and root.right==None:
if(root.val==target):
path.append(root.val)
self.ans.append(path[::])
return
dfs(root.left,target-root.val,path+[root.val])
dfs(root.right,target-root.val,path+[root.val])
self.ans=[]
dfs(root,target,[])
return self.ans129. 求根到叶子节点数字之和
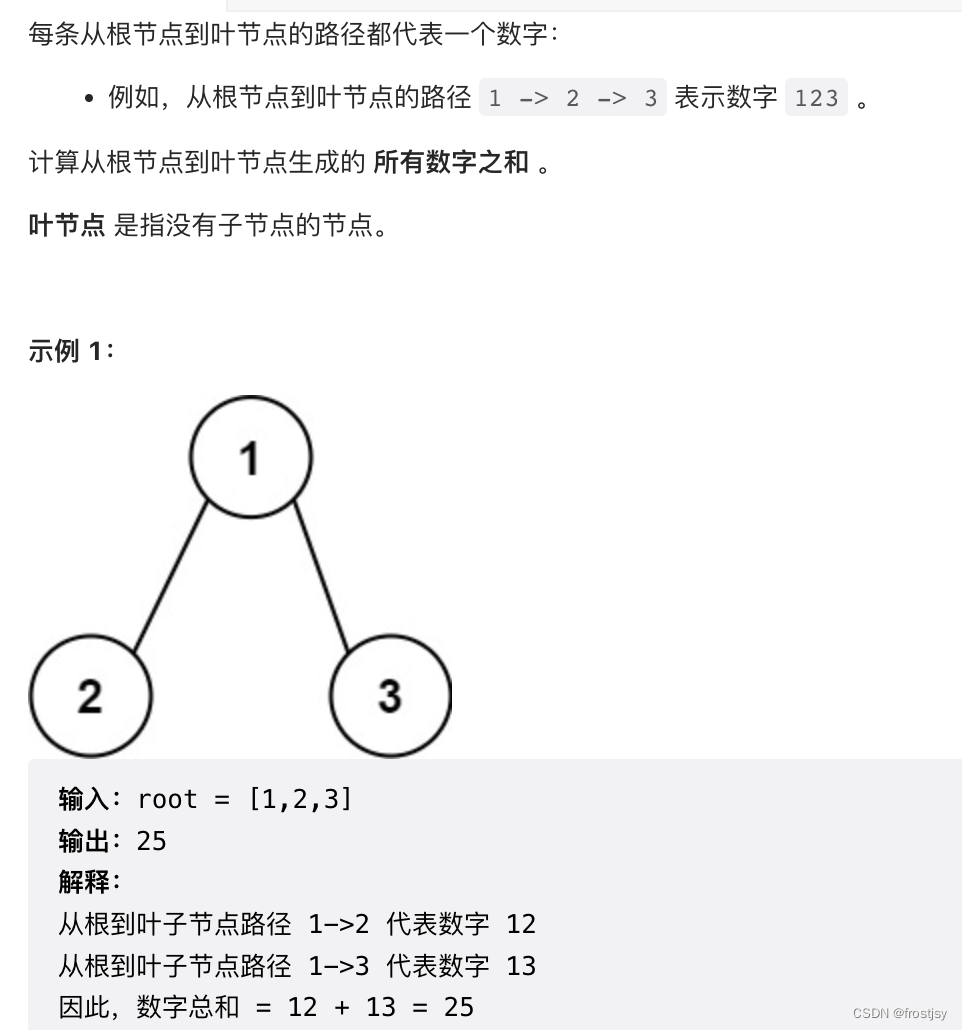
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sumNumbers(self, root: Optional[TreeNode]) -> int:
if root==None:
return 0
self.ans=0
def dfs(root,sumT):
if root==None:
return 0
if root.left==None and root.right==None:
sumT=10*sumT+root.val
self.ans+=sumT
return
dfs(root.left,10*sumT+root.val)
dfs(root.right,10*sumT+root.val)
dfs(root,0)
return self.ans
226. 翻转二叉树
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if root==None:
return None
left_t=self.invertTree(root.left)
right_t=self.invertTree(root.right)
root.left=right_t
root.right=left_t
return root652. 寻找重复的子树
class Solution:
def findDuplicateSubtrees(self, root: Optional[TreeNode]) -> List[Optional[TreeNode]]:
def dfs(node: Optional[TreeNode]) -> str:
if not node:
return ""
serial = "".join([str(node.val), "(", dfs(node.left), ")(", dfs(node.right), ")"])
if (tree := seen.get(serial, None)):
repeat.add(tree)
else:
seen[serial] = node
return serial
seen = dict()
repeat = set()
dfs(root)
return list(repeat)
链接:https://leetcode.cn/problems/find-duplicate-subtrees/solution/xun-zhao-zhong-fu-de-zi-shu-by-leetcode-zoncw/222. 完全二叉树的节点个数
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def countNodes(self, root: Optional[TreeNode]) -> int:
if root==None:
return 0
q=[root]
ans=1
while q:
t=[]
for cur in q:
if cur.left:
t.append(cur.left)
if cur.right:
t.append(cur.right)
q=t
ans+=len(q)
return ans
class Solution:
def countNodes(self, root: Optional[TreeNode]) -> int:
if root is None:
return 0
left=self.countNodes(root.left)
right=self.countNodes(root.right)
return left+right+1257. 二叉树的所有路径
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
if root==None:
return []
self.ans=[]
def dfs(root,path):
if(root==None):
return []
if root.left==None and root.right==None:
path.append(root.val)
self.ans.append("->".join(map(str,path[::])))
return
dfs(root.left,path+[root.val])
dfs(root.right,path+[root.val])
dfs(root,[])
return self.ans剑指 Offer 32 - III. 从上到下打印二叉树 III
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
if root==None:
return []
q=[root]
ans=[]
i=0
while q:
t=[]
res=[]
for cur in q:
res.append(cur.val)
if cur.left:
t.append(cur.left)
if cur.right:
t.append(cur.right)
q=t
if i%2==1:
res=res[::-1]
ans.append(res)
i+=1
return ans
剑指 Offer 07. 重建二叉树
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
if len(preorder)==0 or len(inorder)==0:
return None
val=preorder[0]
idx=inorder.index(val)
root=TreeNode(val)
left_t=self.buildTree(preorder[1:idx+1],inorder[0:idx])
right_t=self.buildTree(preorder[idx+1:],inorder[idx+1:])
root.left=left_t
root.right=right_t
return root剑指 Offer 54. 二叉搜索树的第k大节点
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def kthLargest(self, root: TreeNode, k: int) -> int:
def dfs(root):
if root==None:
return []
return dfs(root.left)+[root.val]+dfs(root.right)
ans=dfs(root)
# print(ans)
return ans[len(ans)-k]