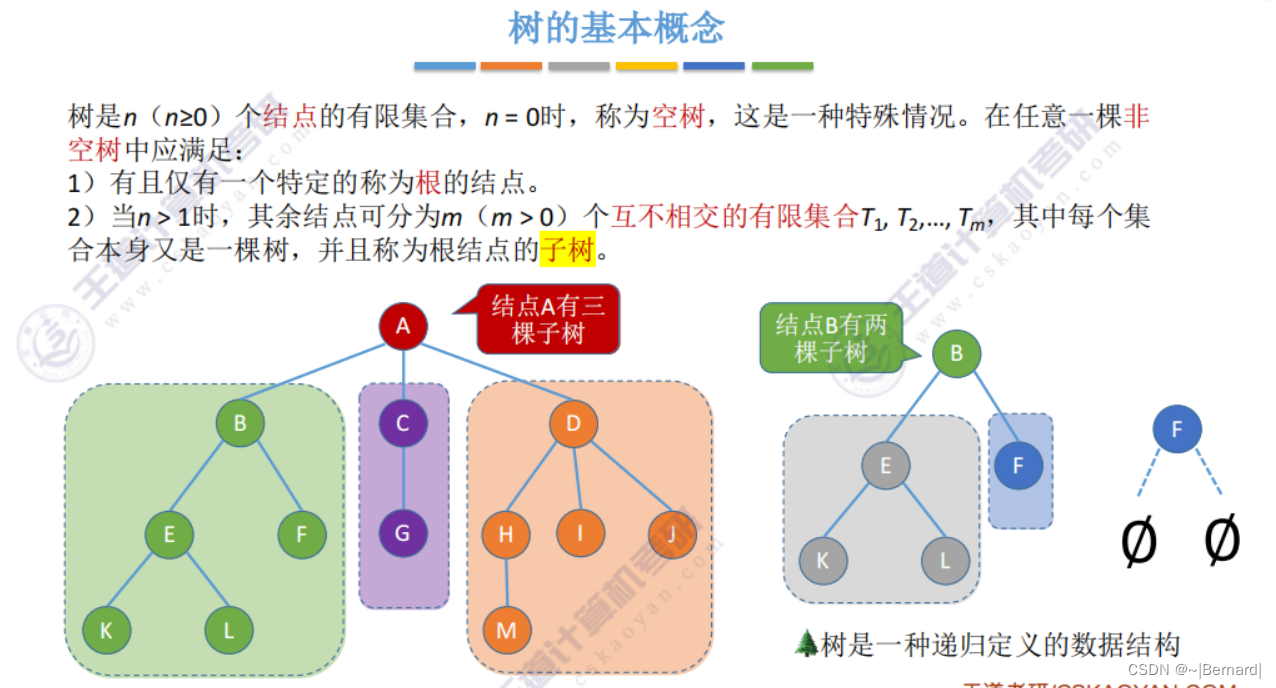
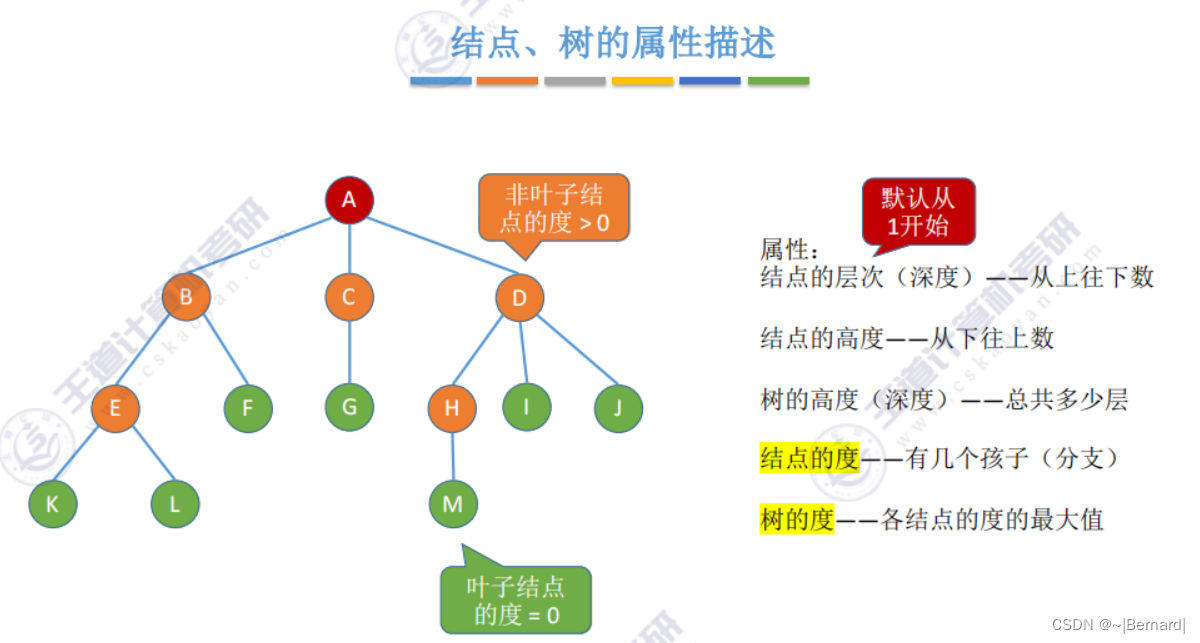
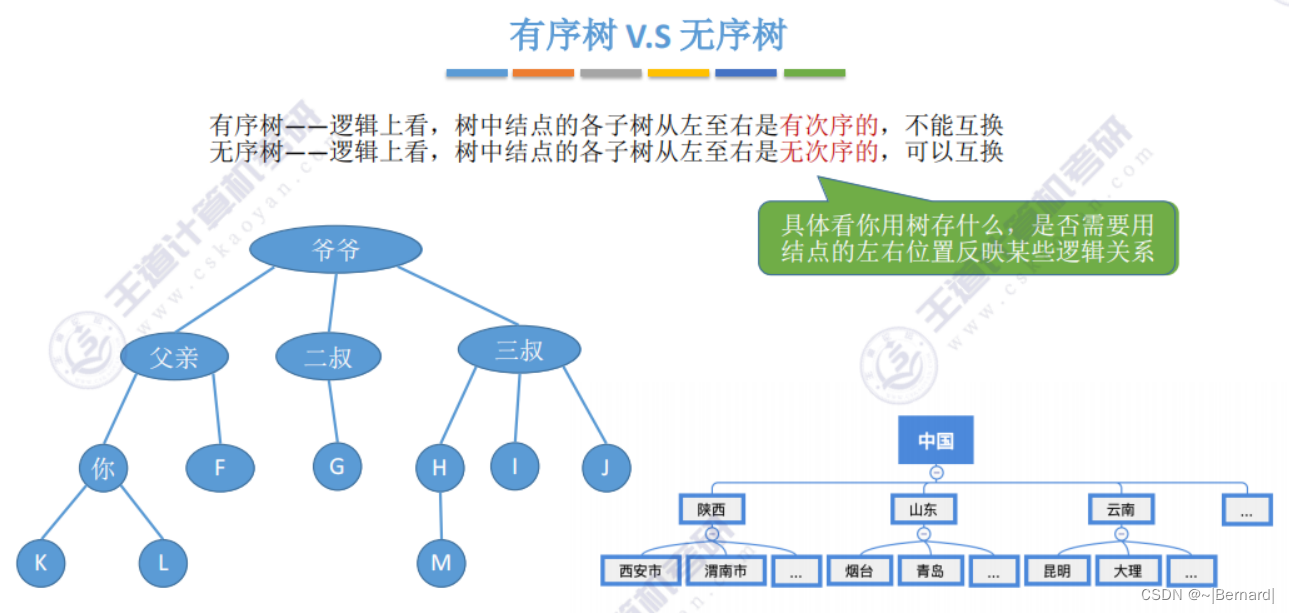
5.1.1 树的定义和基本术语
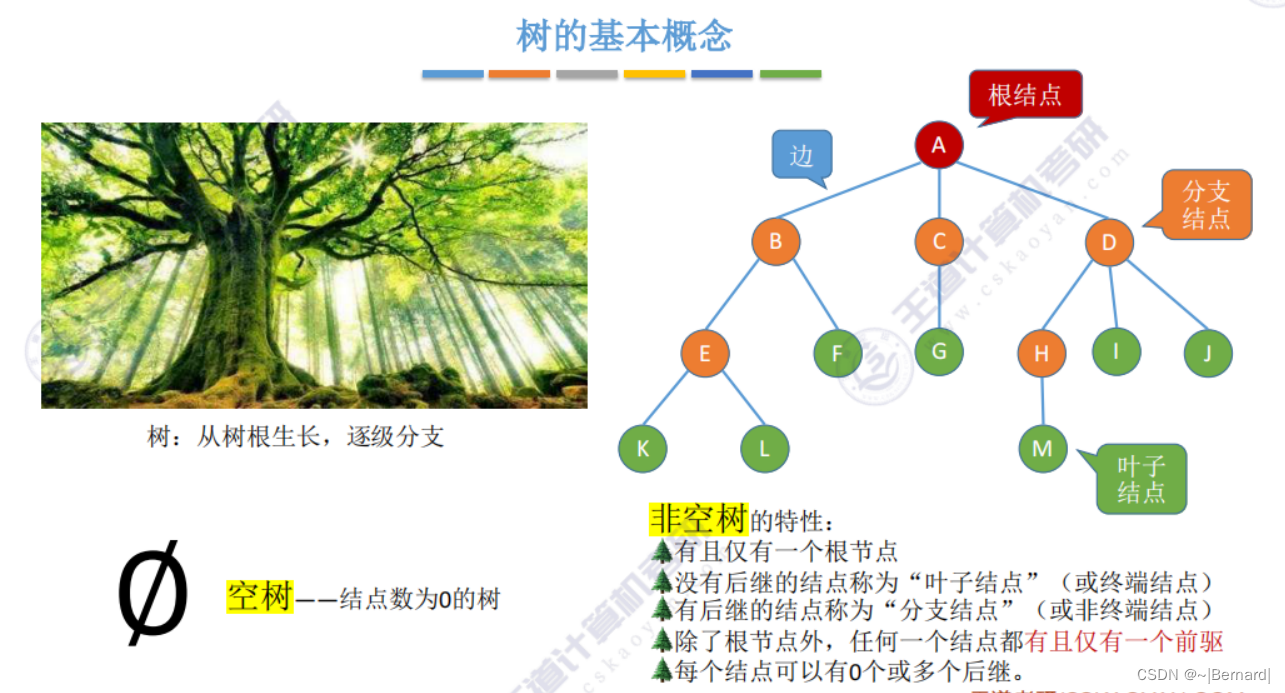
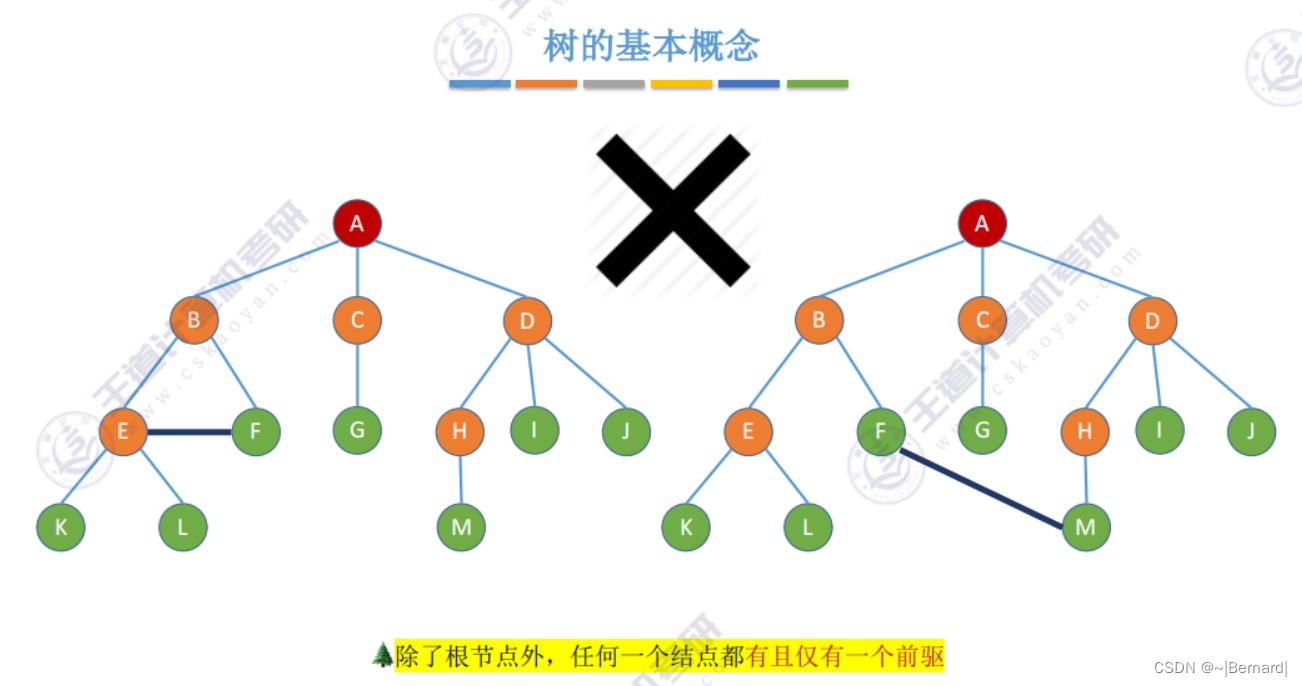

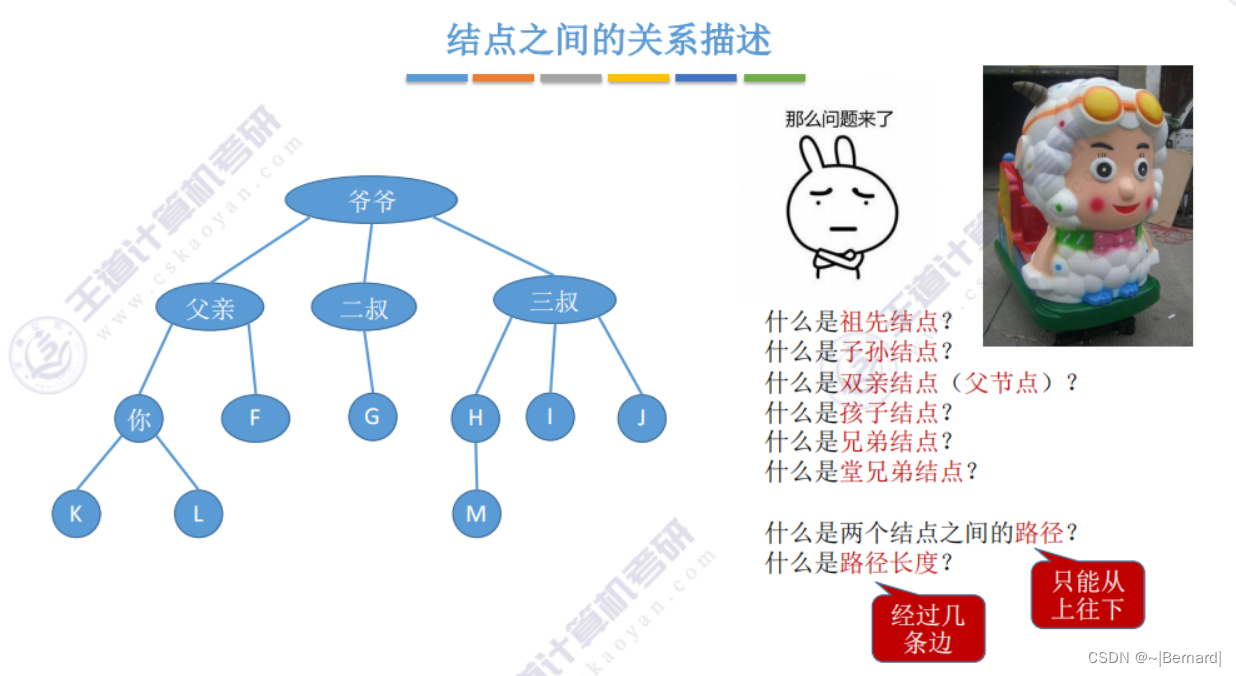
祖先节点:(对于你来说),父亲和爷爷都是祖先节点
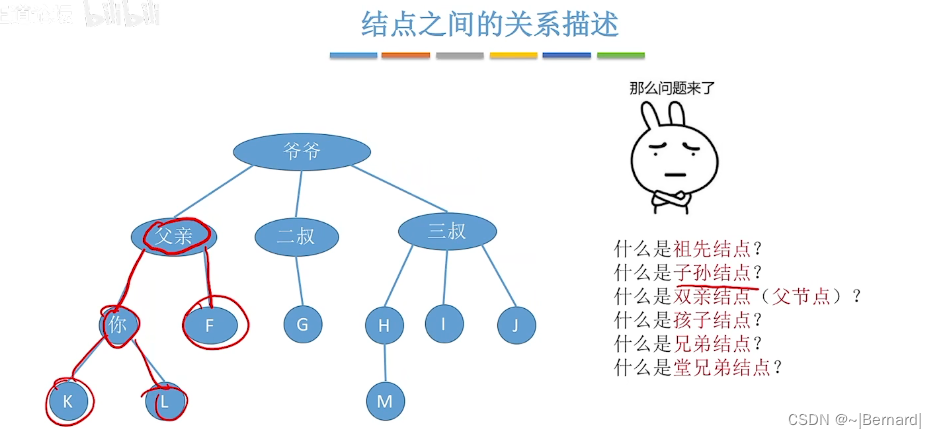
子孙节点:对于父亲来说,父亲下面所有的节点都叫子孙节点
双亲节点(父节点):一个节点的直接前驱就是它的父节点
兄弟节点:例如二叔,三叔都是父亲的兄弟节点
堂兄弟节点:对于你来说,GHIJ节点就是堂兄弟节点
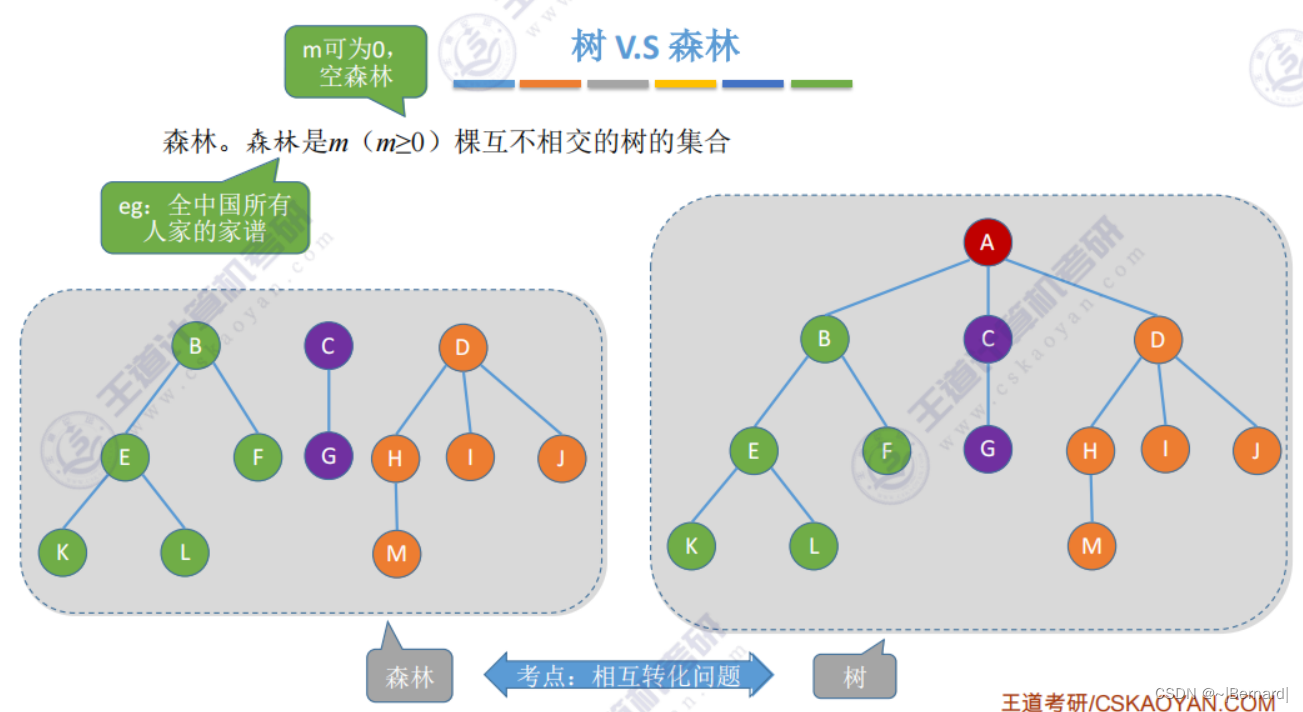
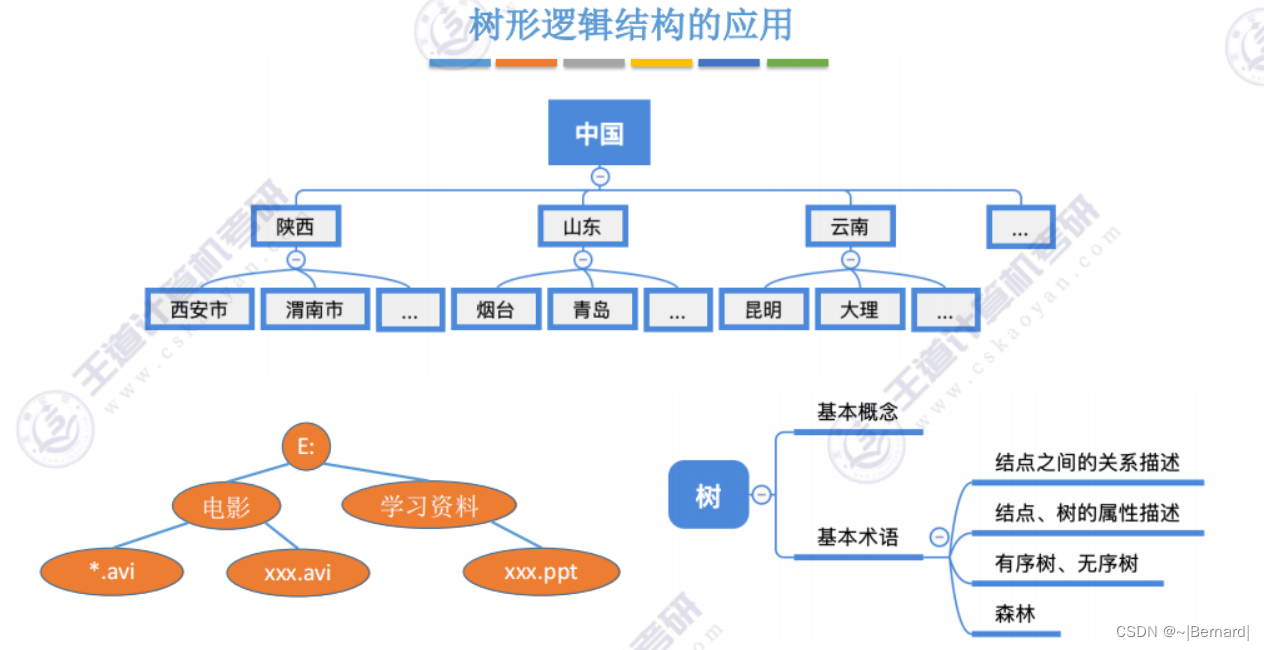
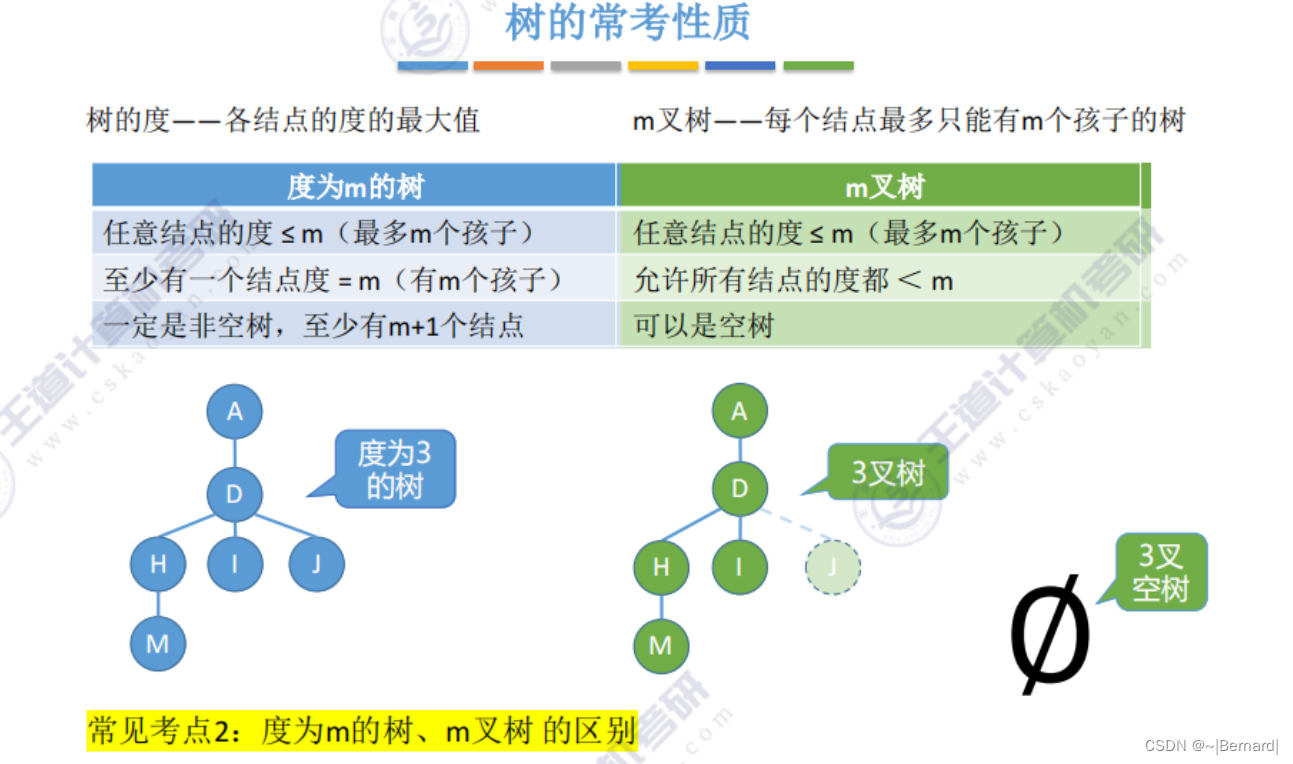
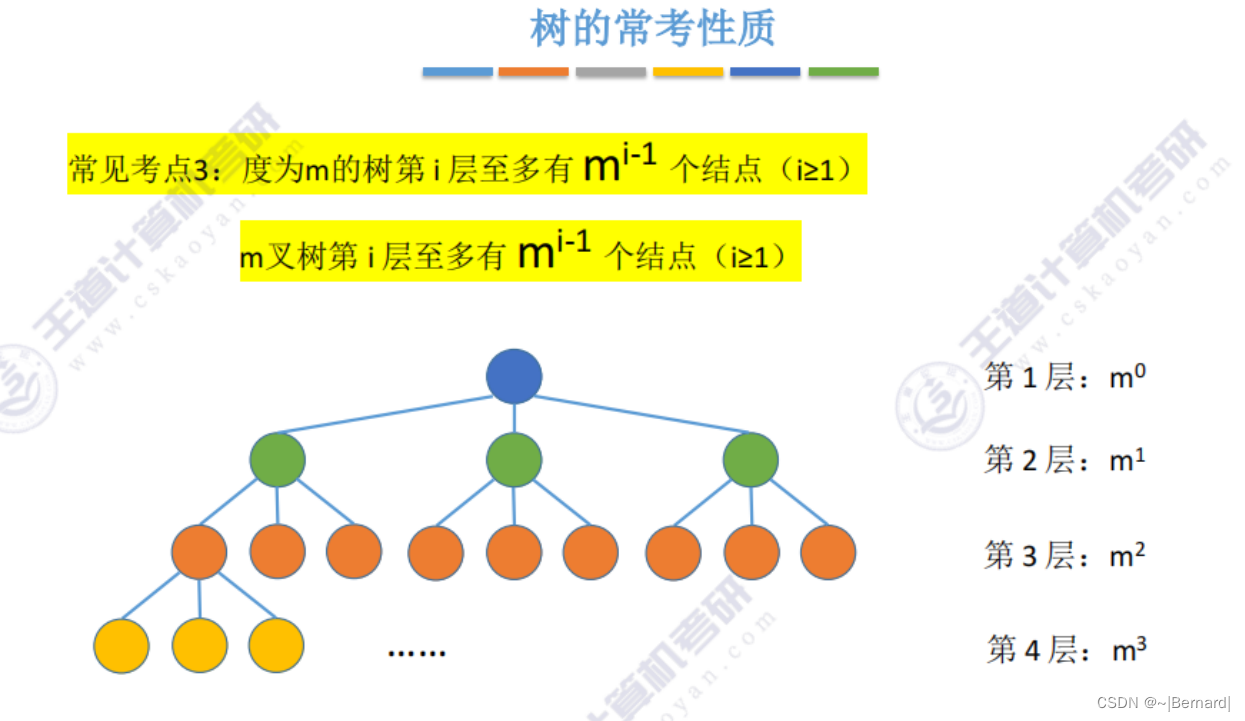
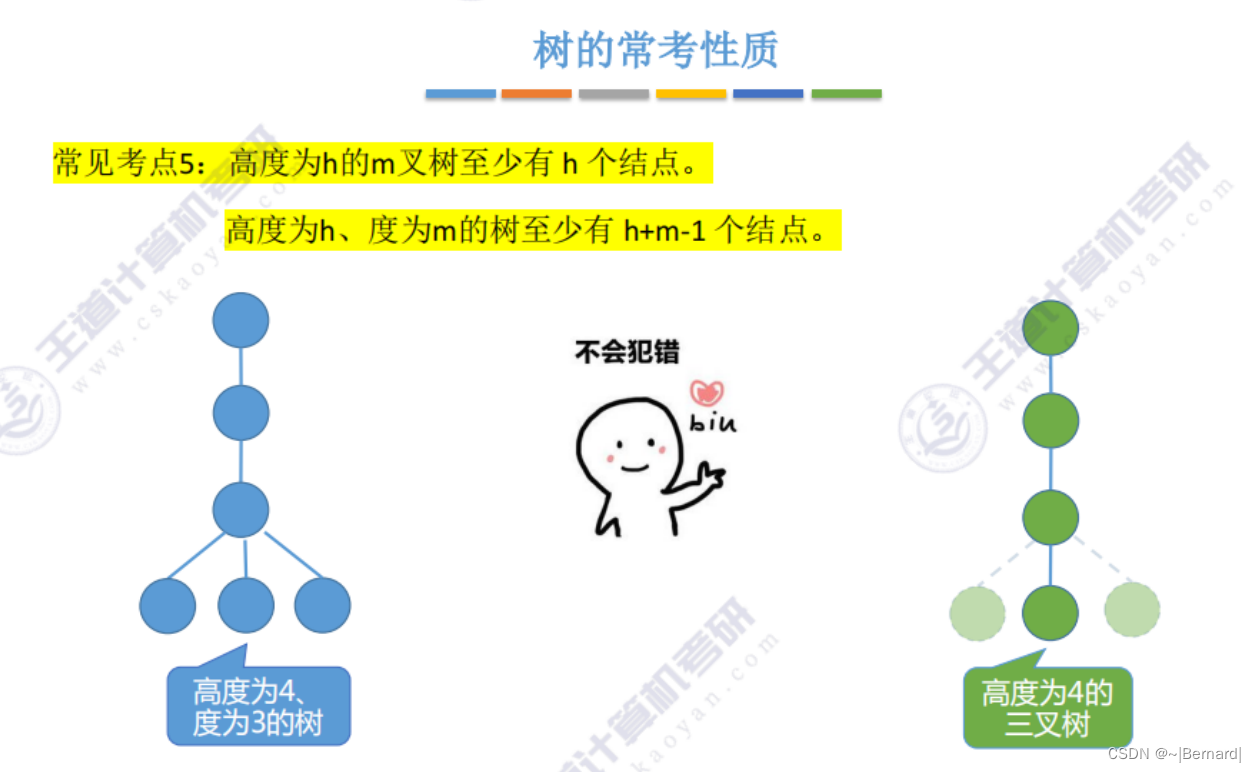
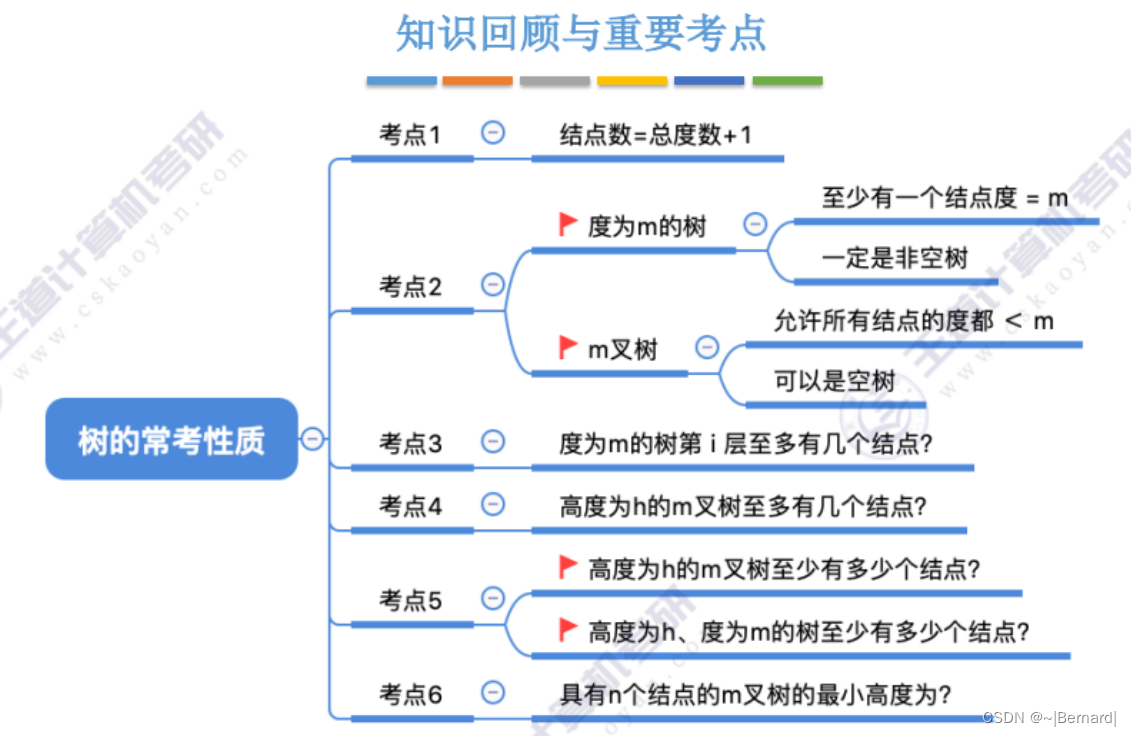
 5.1.2 树的性质
5.1.2 树的性质
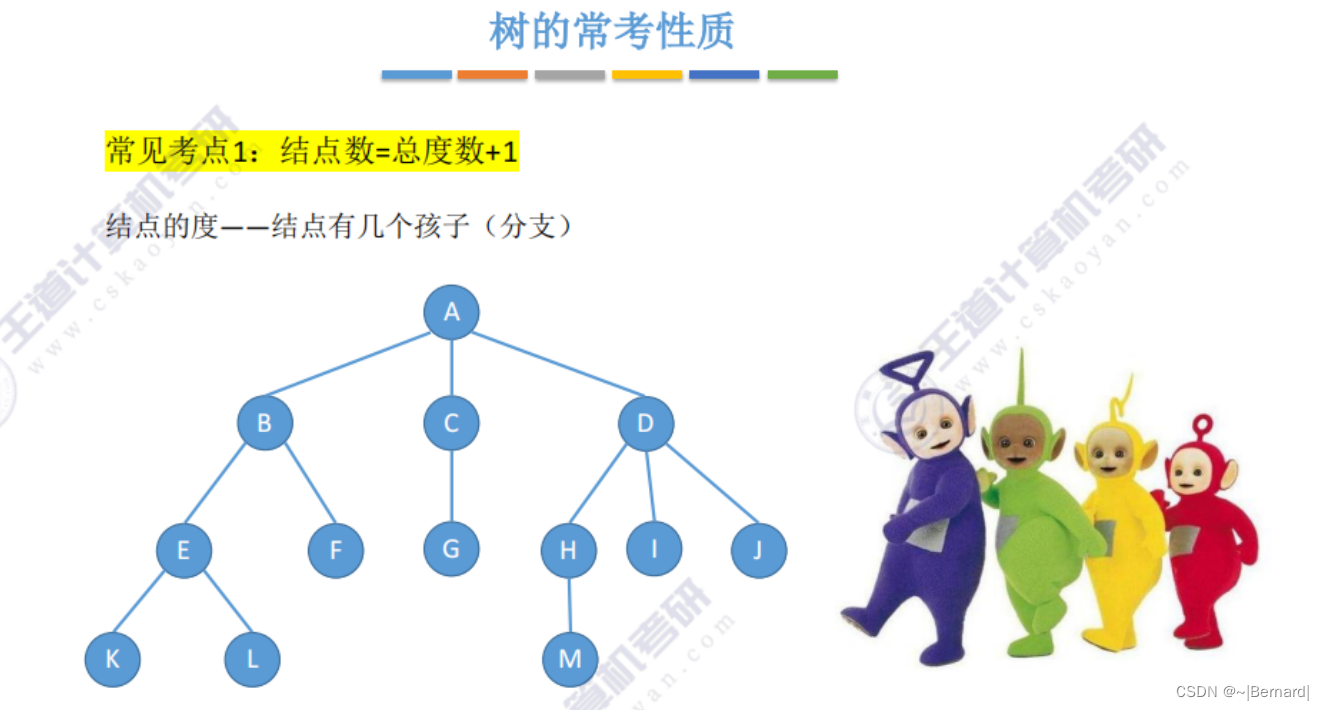
理解:节点数=总度数+1,由于根节点头上是没有边的,所以节点数比总度数多一个。
助记:天线宝宝


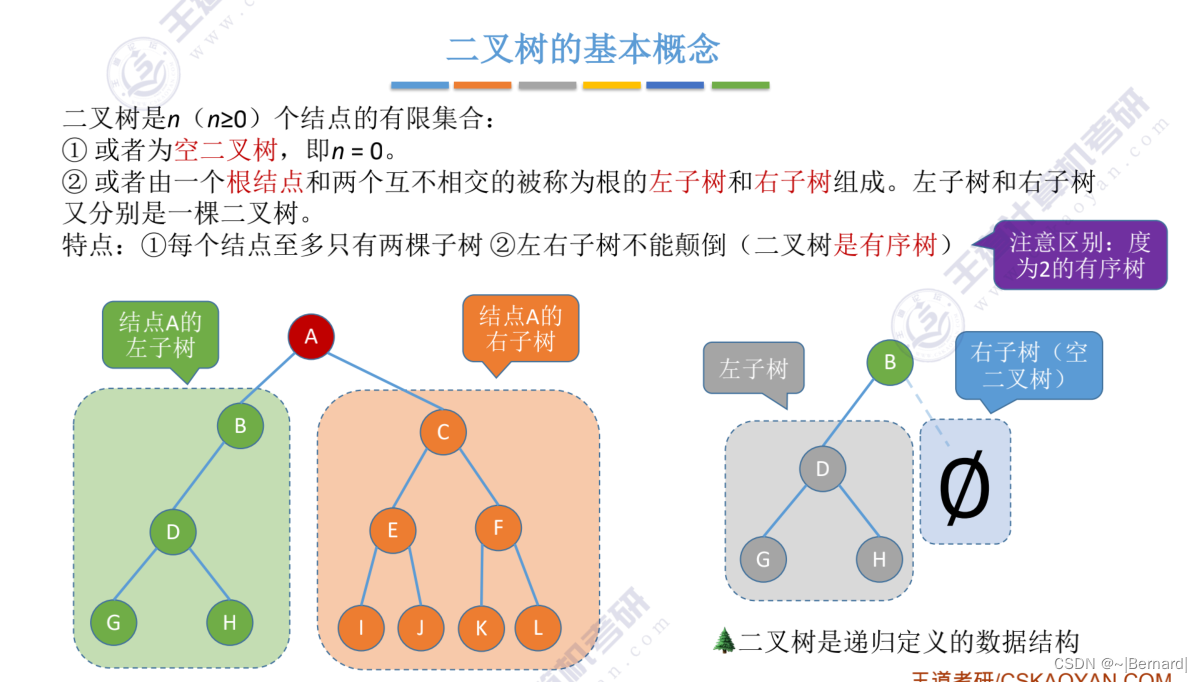
 5.2.1 二叉树的定义和基本术语
5.2.1 二叉树的定义和基本术语

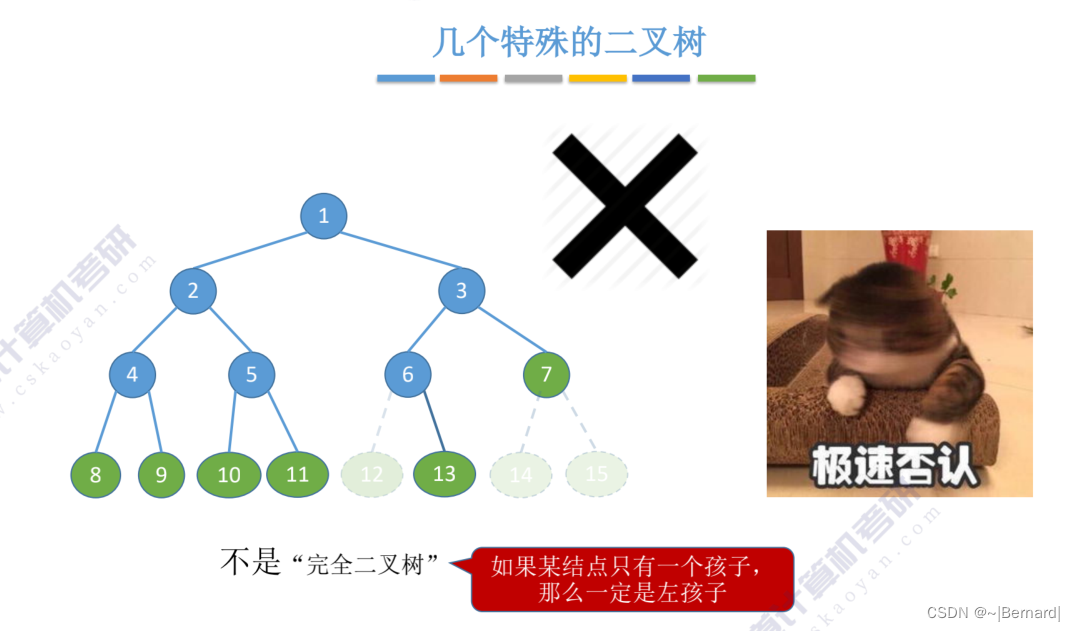
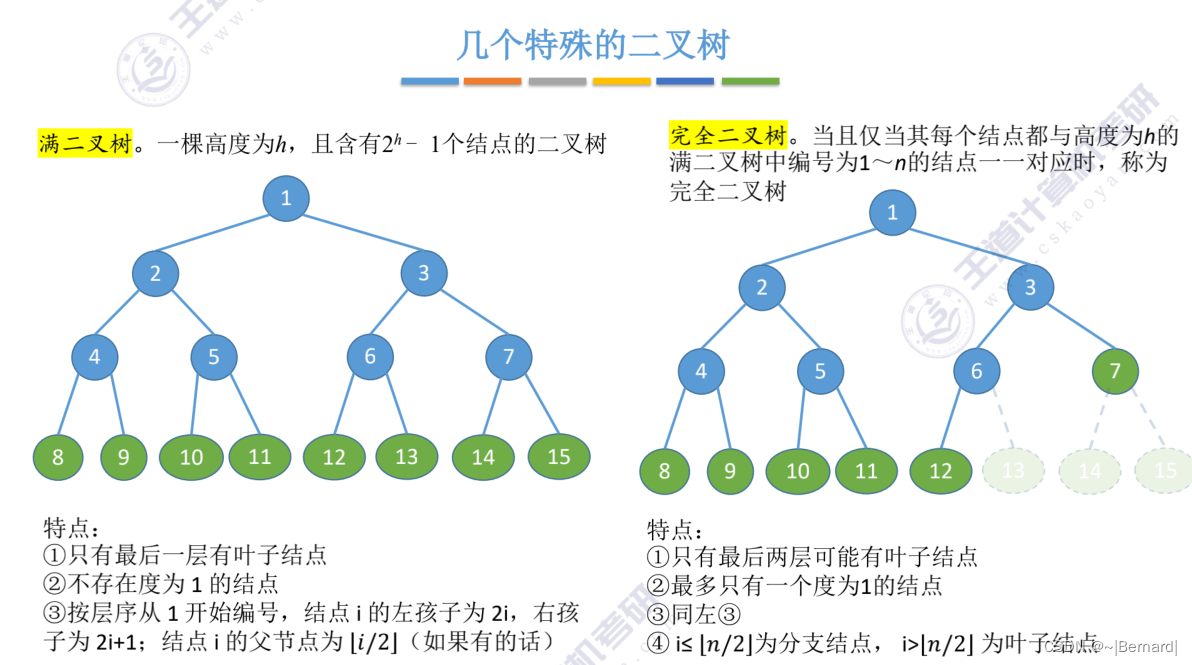 完全二叉树相较于满二叉树只是去掉了编号较大的节点,并且去掉节点后编号保持不变。
完全二叉树相较于满二叉树只是去掉了编号较大的节点,并且去掉节点后编号保持不变。
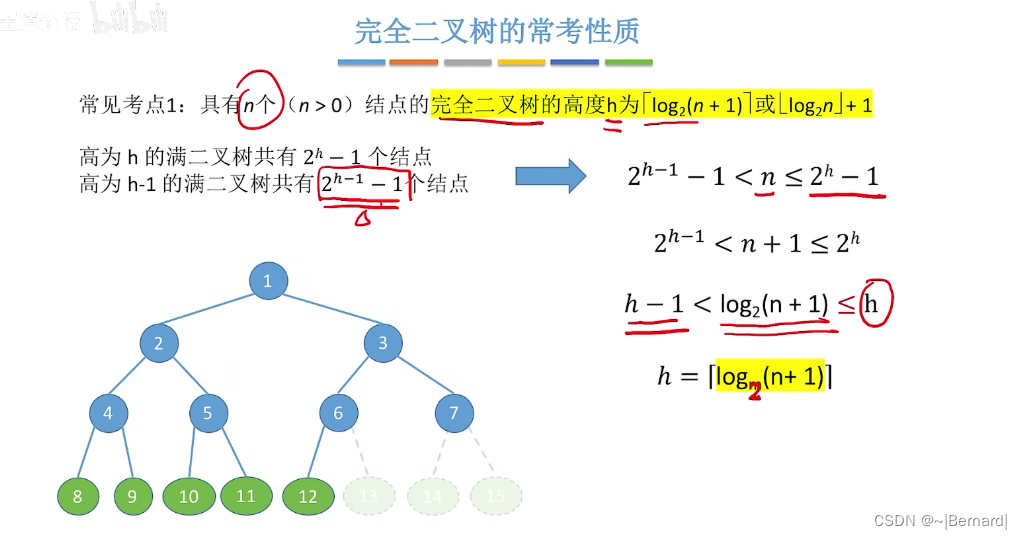
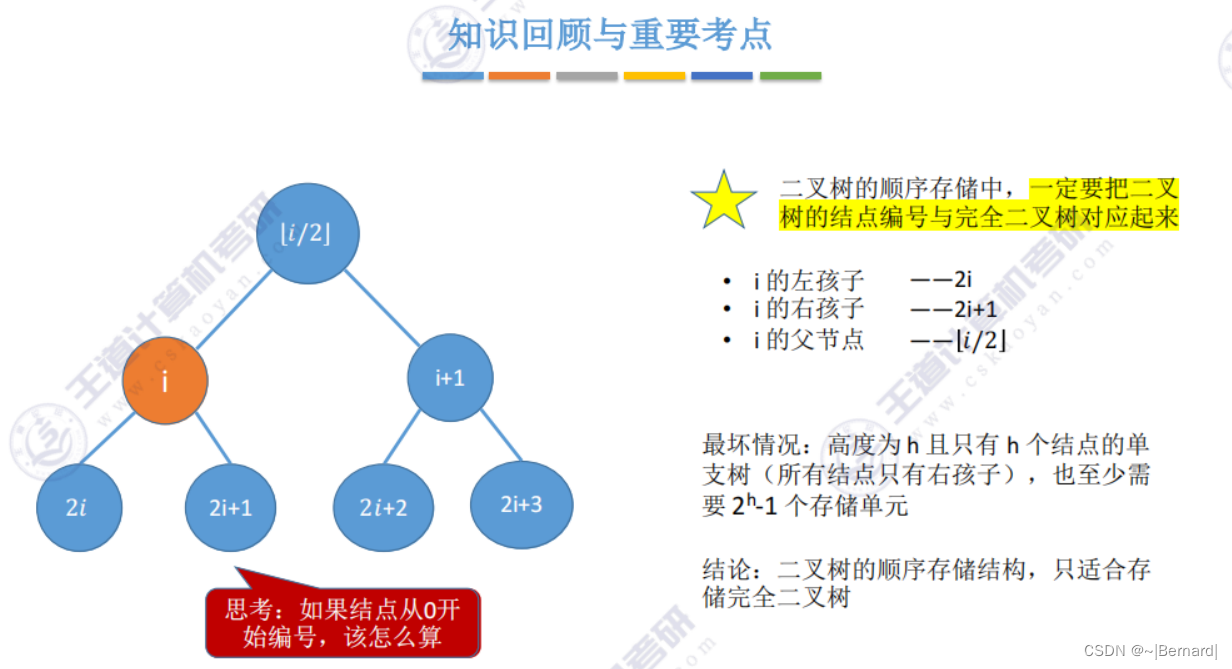
注意:都是向下取整。
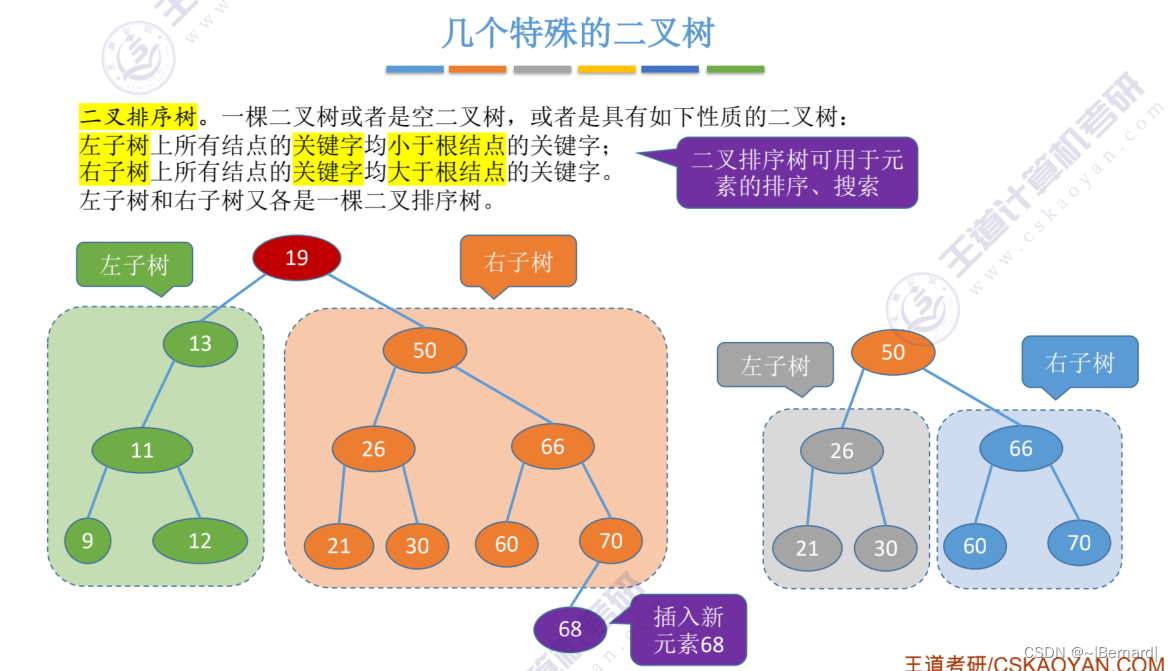
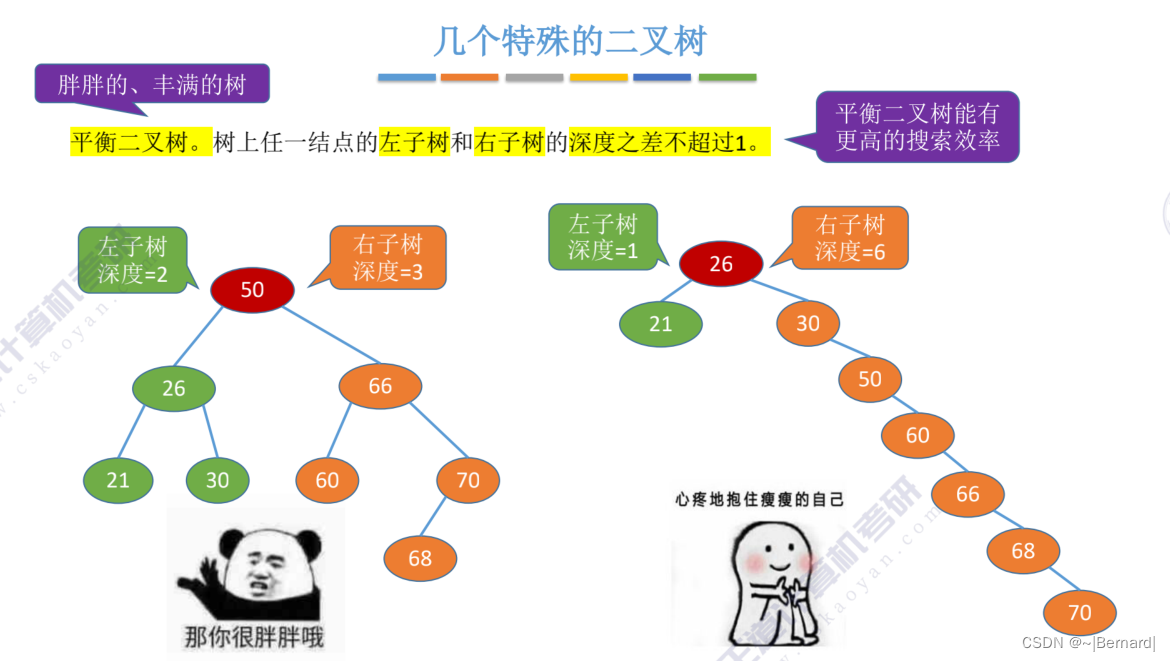

5.2.2 二叉树的性质
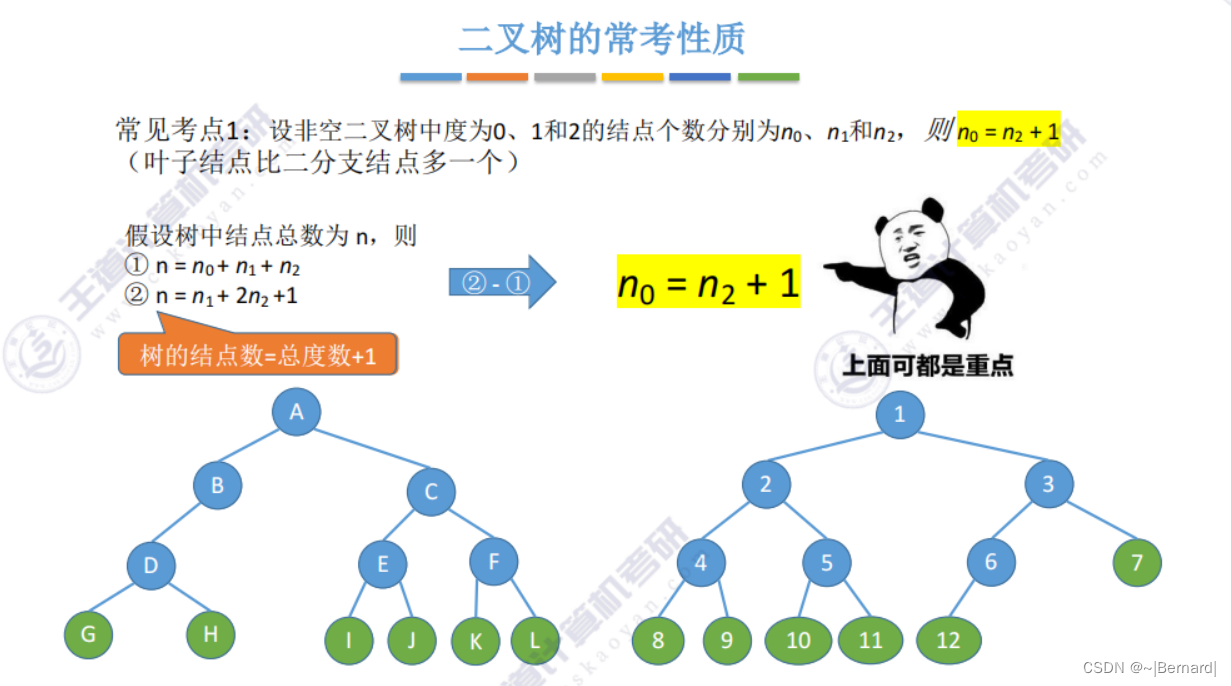
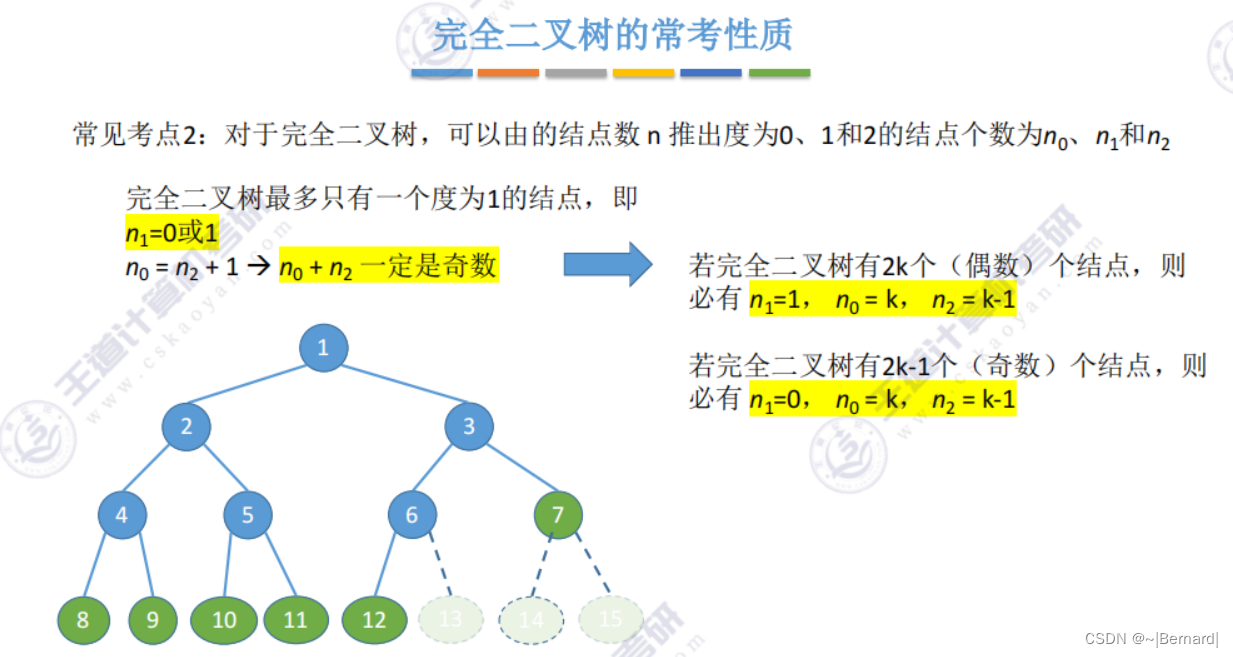
叶子节点的个数比度为2的节点个数多一个。
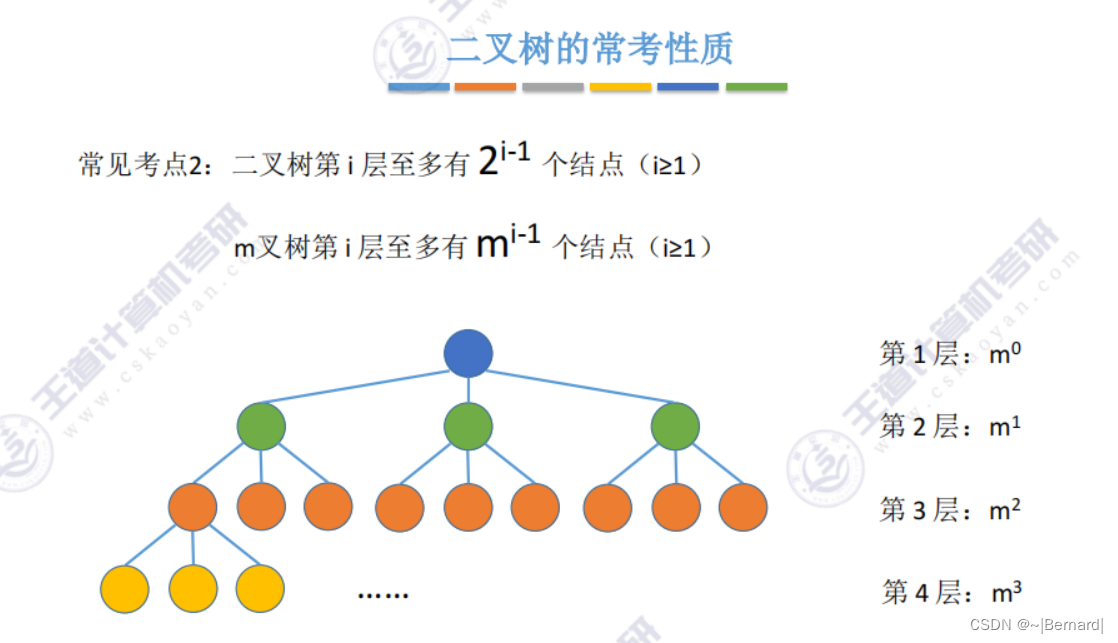
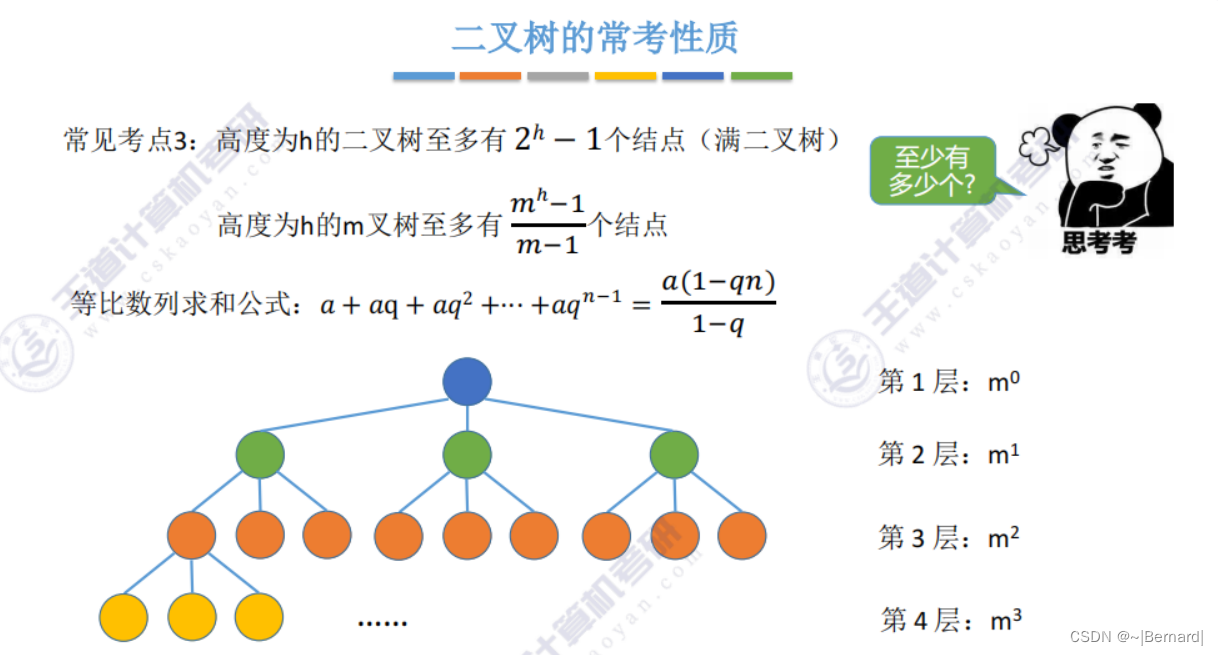


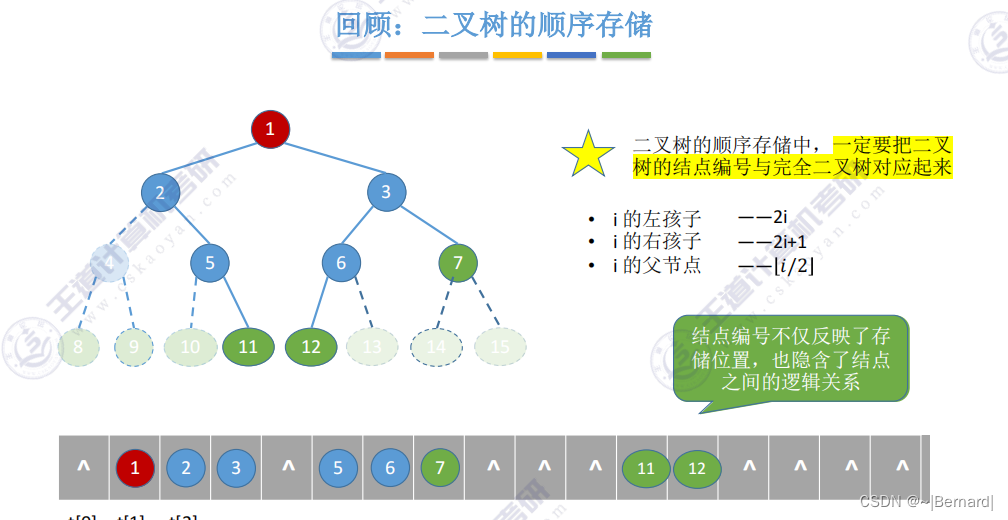
5.2.3 二叉树的存储结构

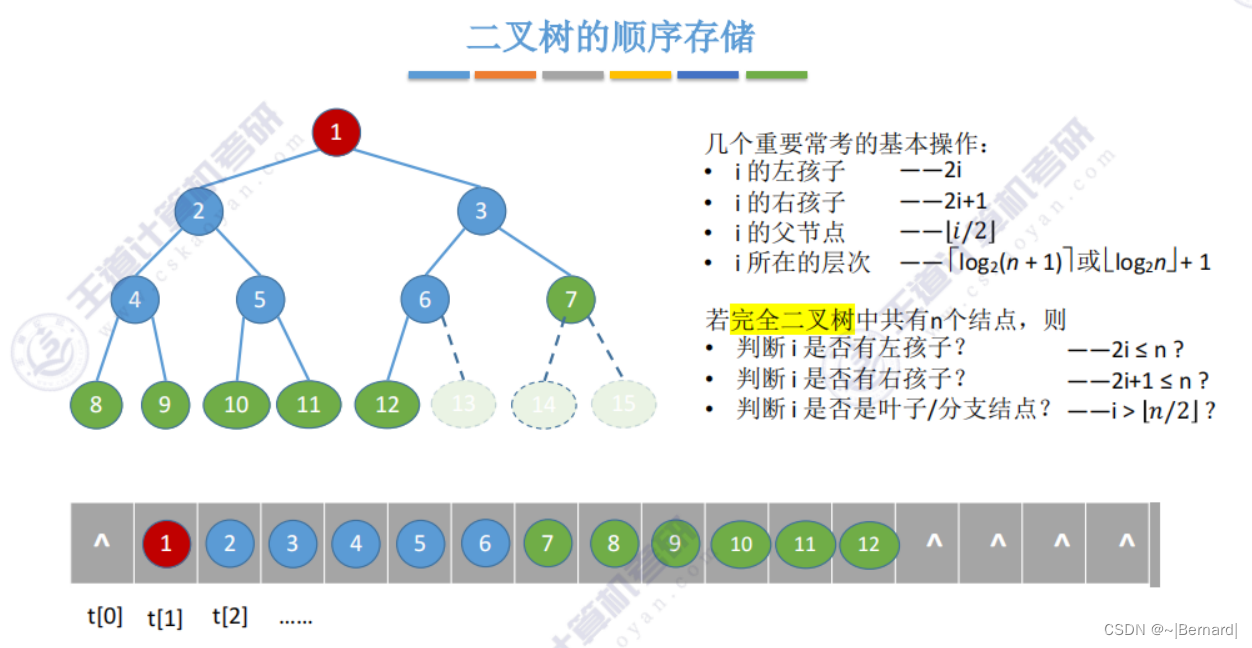
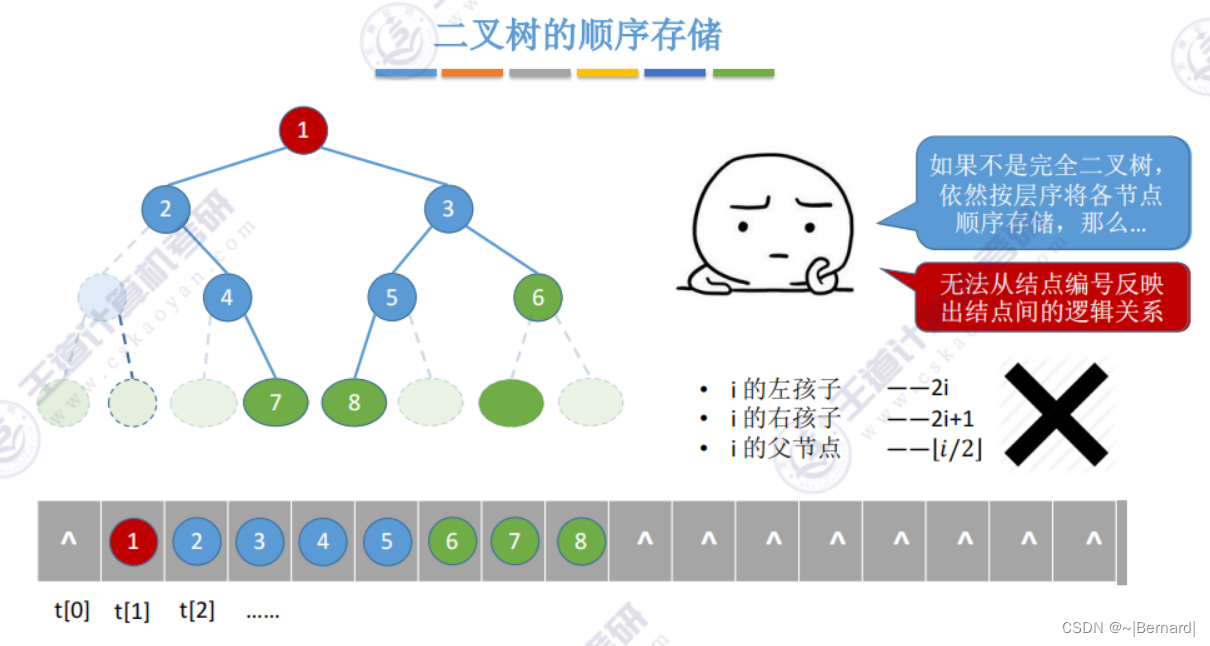

若在非完全二叉树中,用顺序存储的方式就无法用图中方式来判断一个节点是否有左孩子和右孩子。只能够用结构体中的empty值来判断.

二叉树的顺序存储结构只适合存储完全二叉树
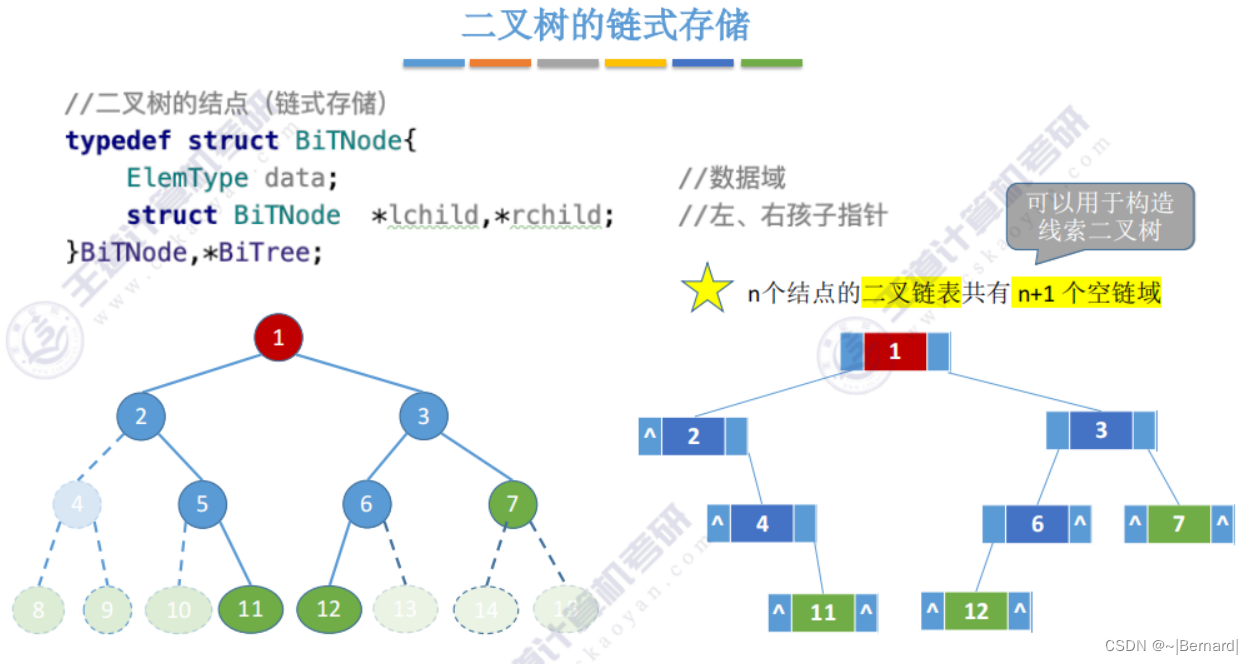
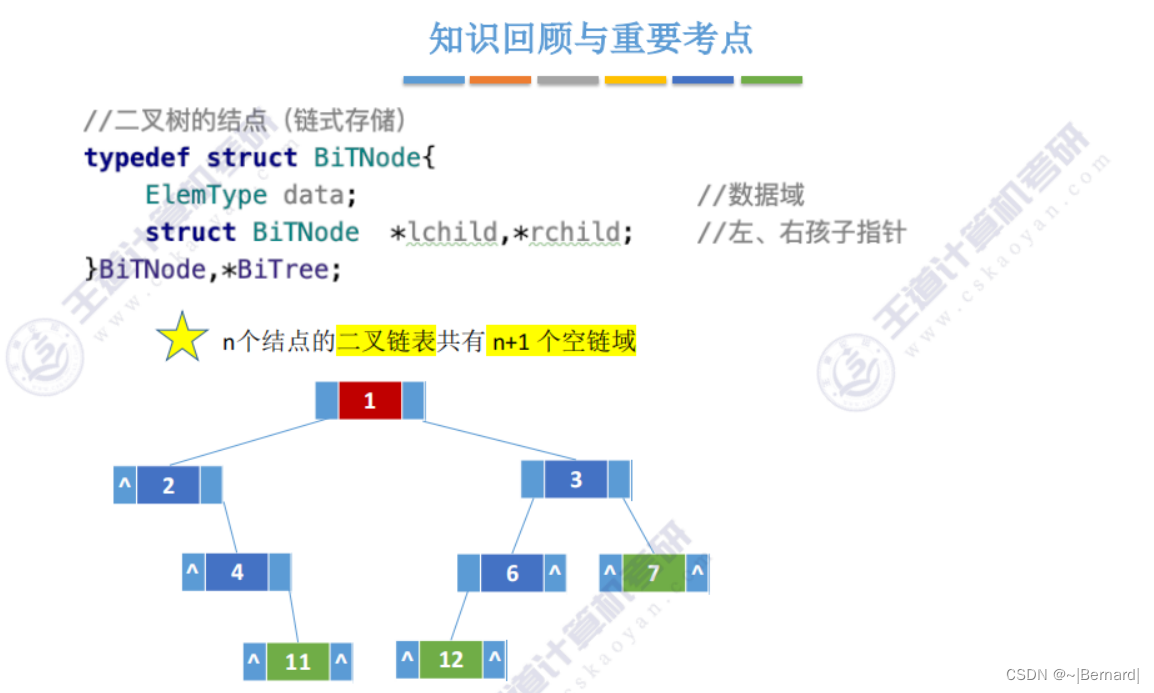
链式存储方式中n个节点,就会有2n个指针域,除了根节点以外,其他每一个节点的头上都会连有一个指针,即n-1个指针域,也就是说2n个指针域中会有n+1个指针域是指向null(空域)的
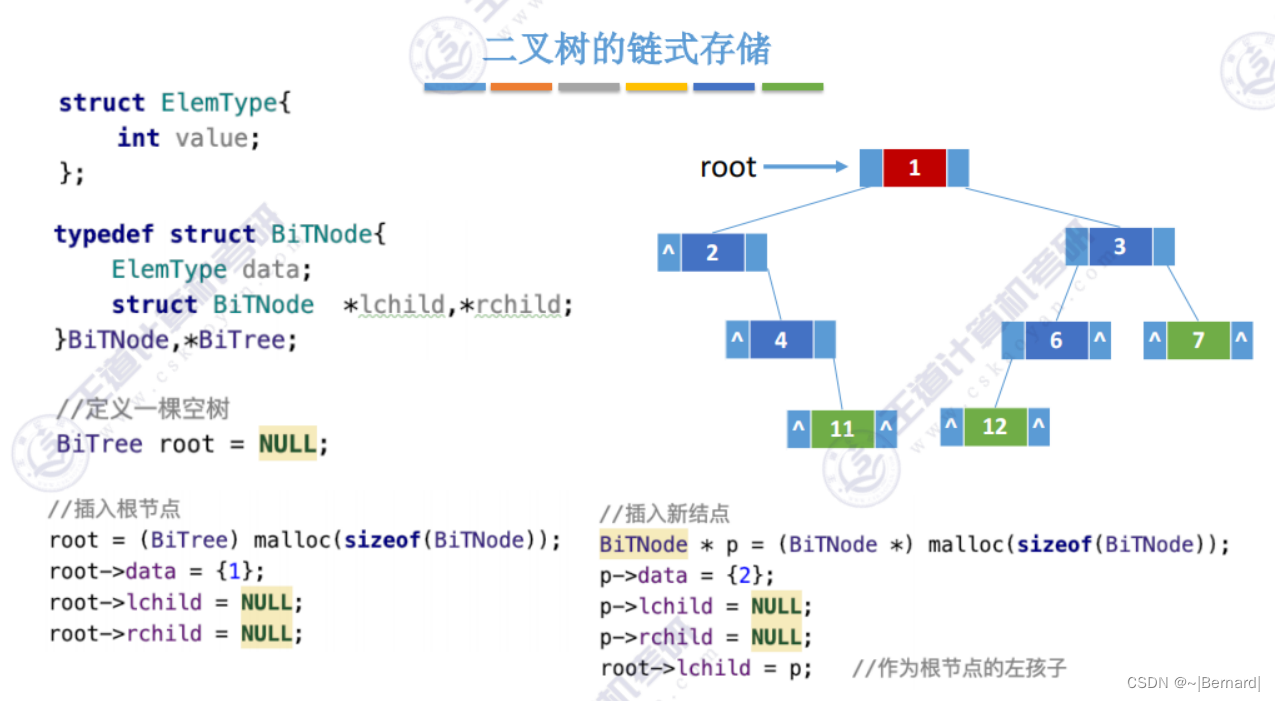
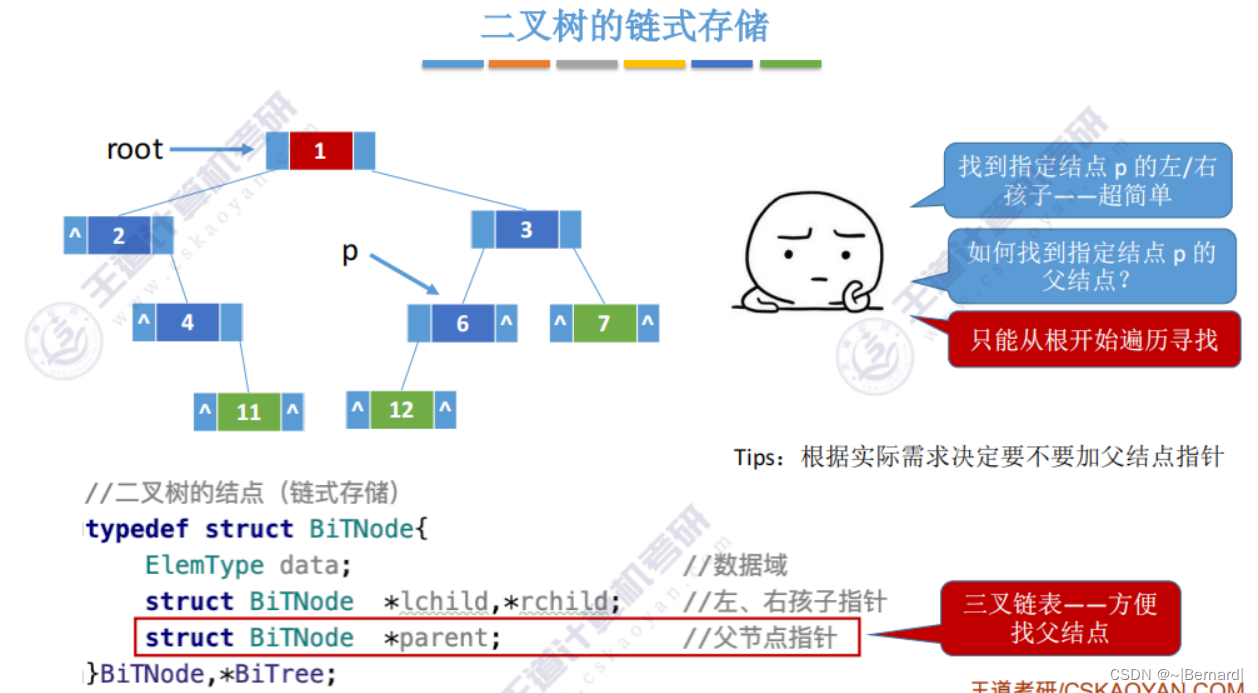
 5.3.1 二叉树的先中后序遍历
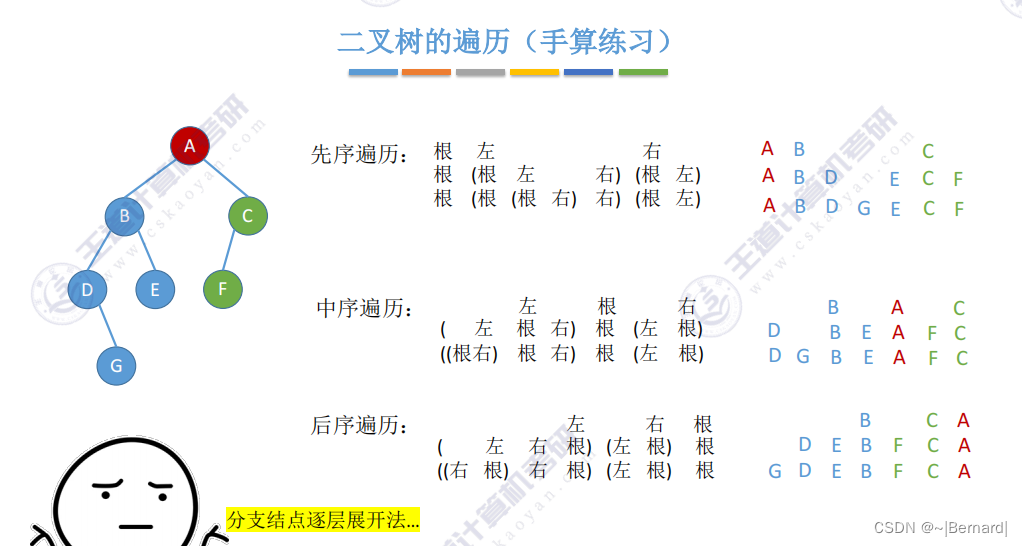
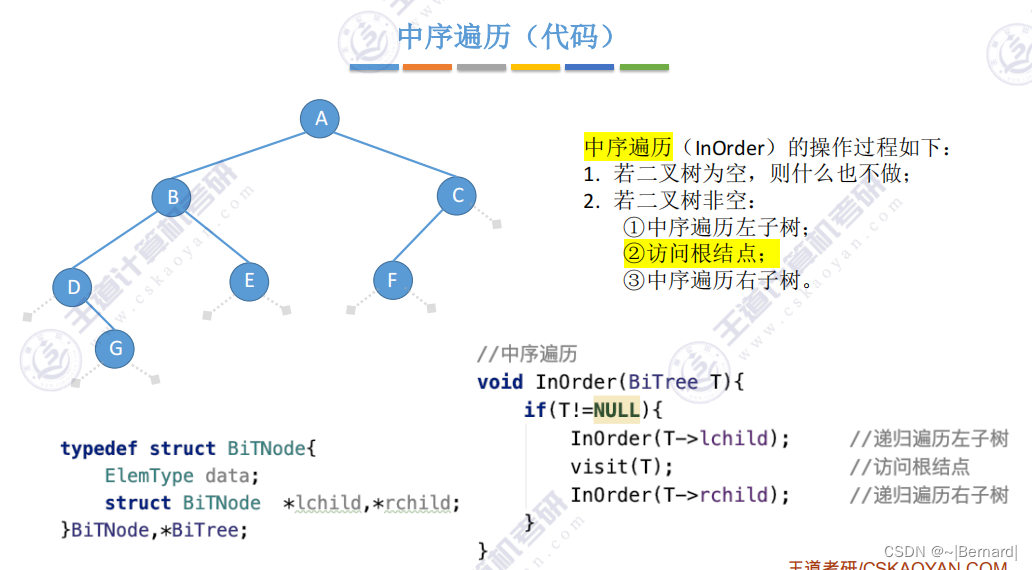
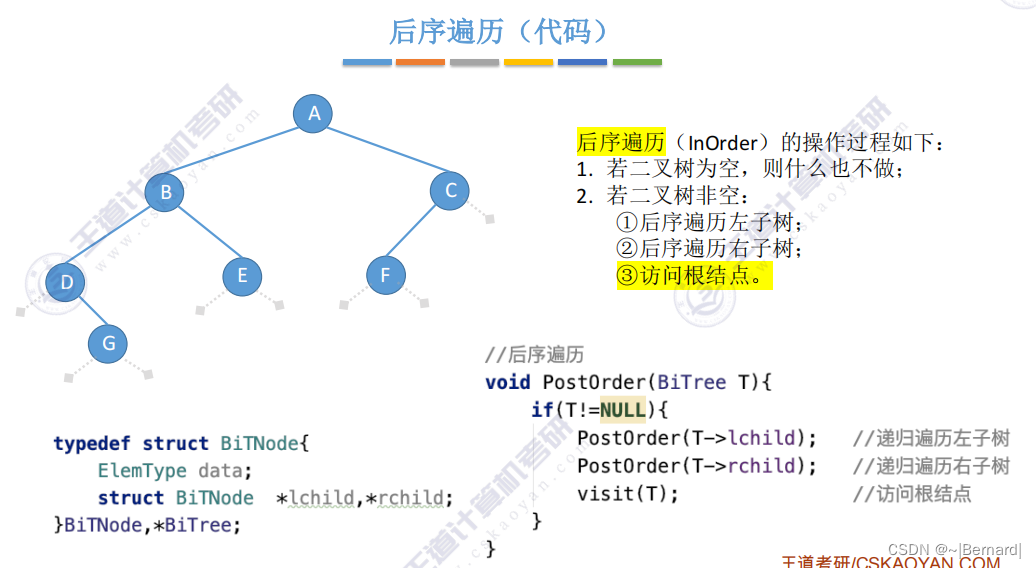
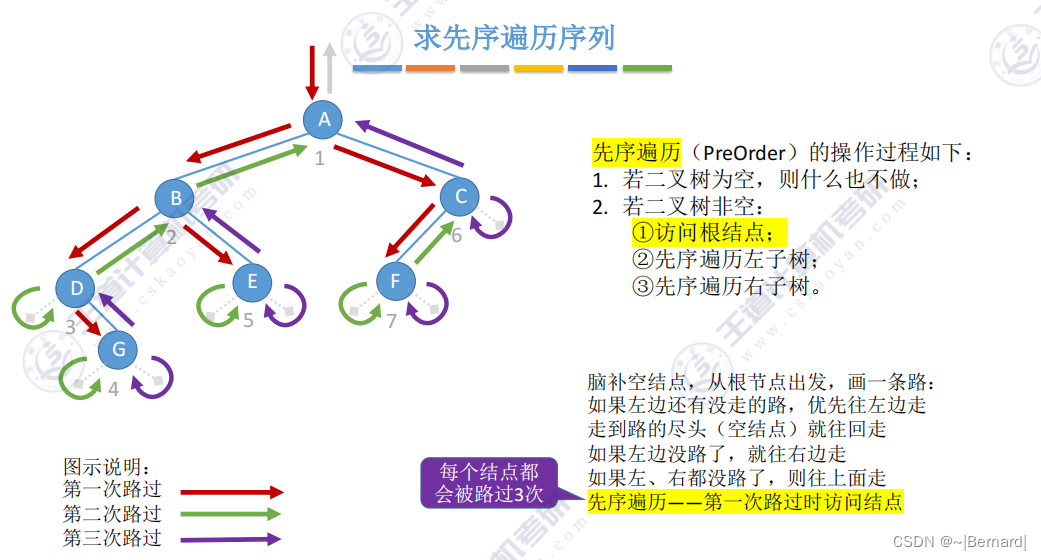
5.3.1 二叉树的先中后序遍历
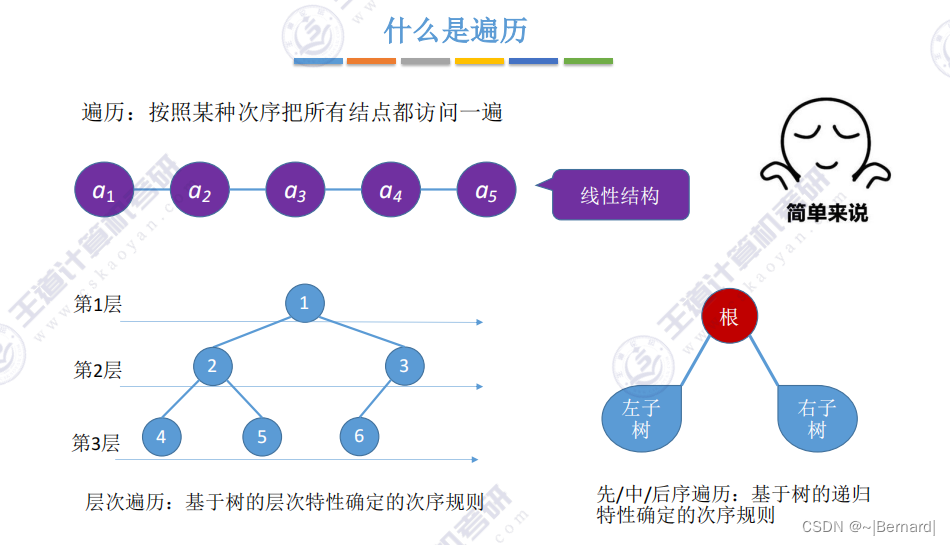
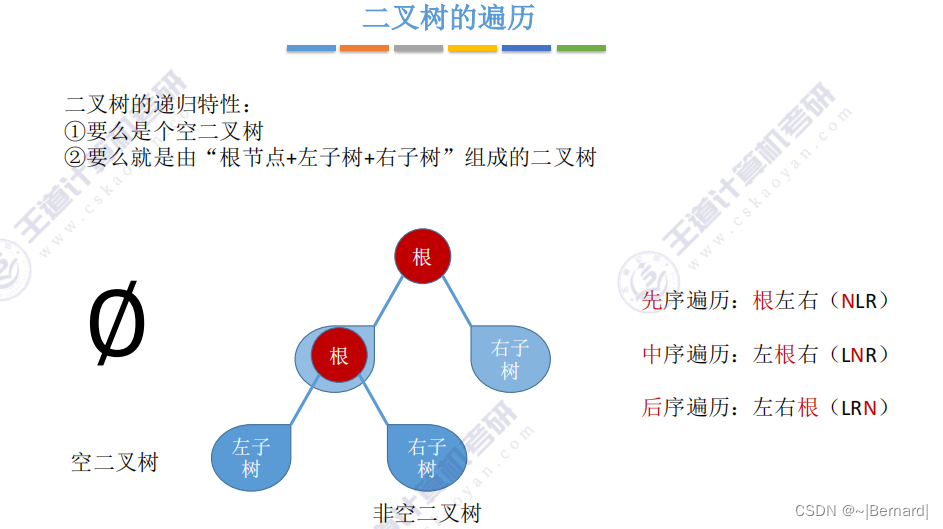
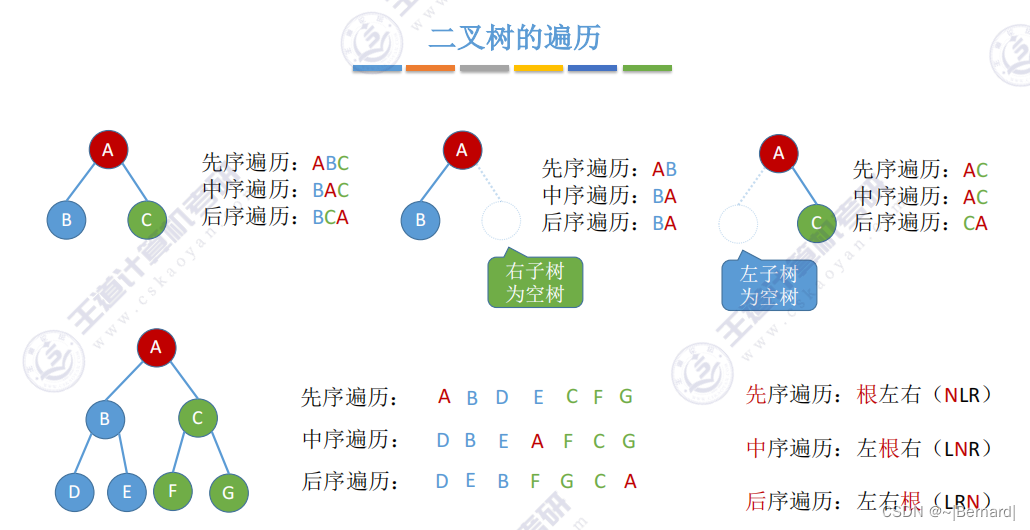
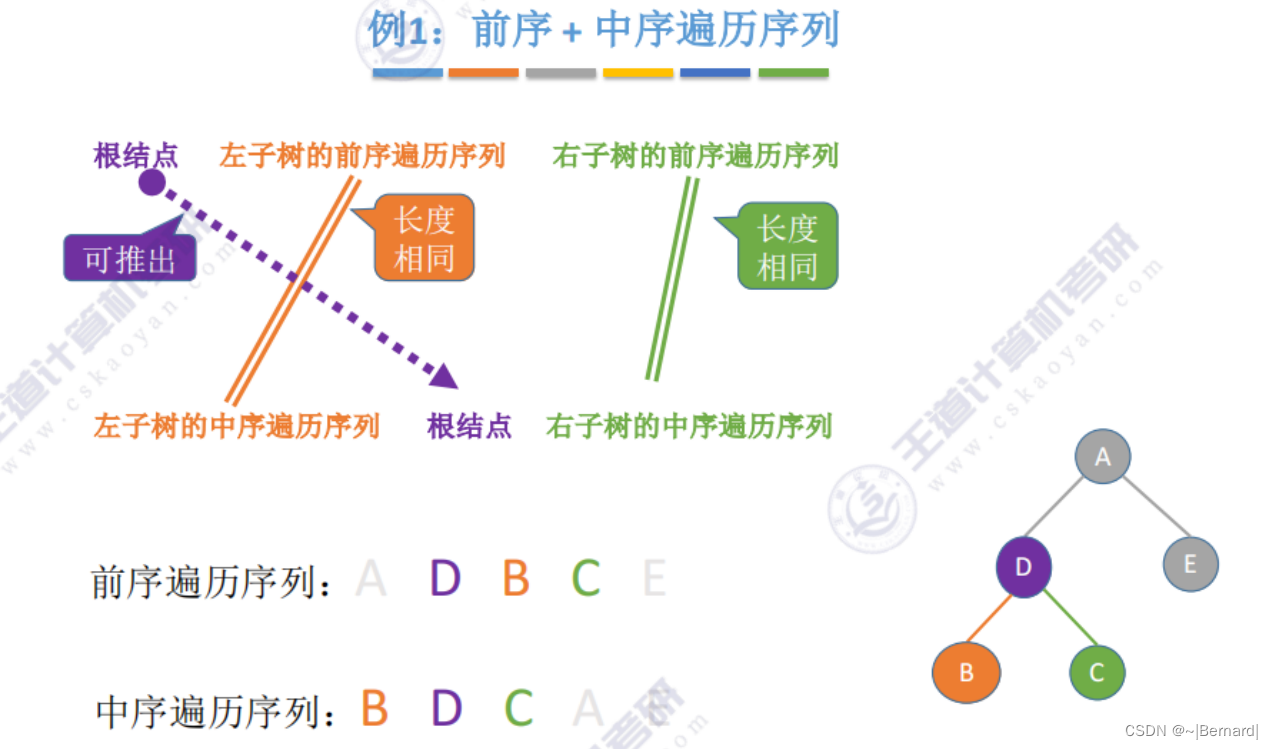
由于B和C是分支节点而不是叶子节点,所以再对B和C节点分别递归进行相应的遍历.


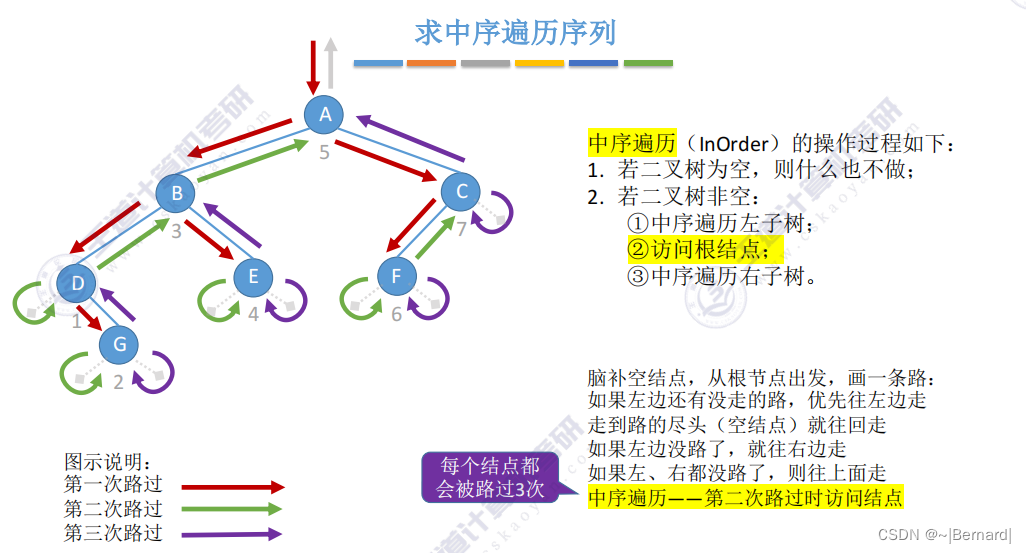
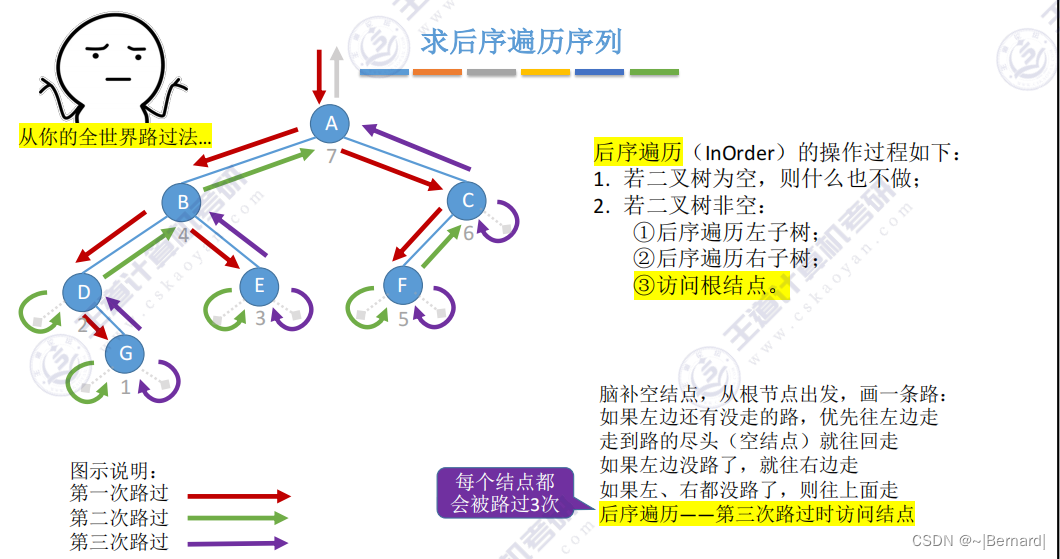 递归遍历算法的空间复杂度为O(h+1)
递归遍历算法的空间复杂度为O(h+1)
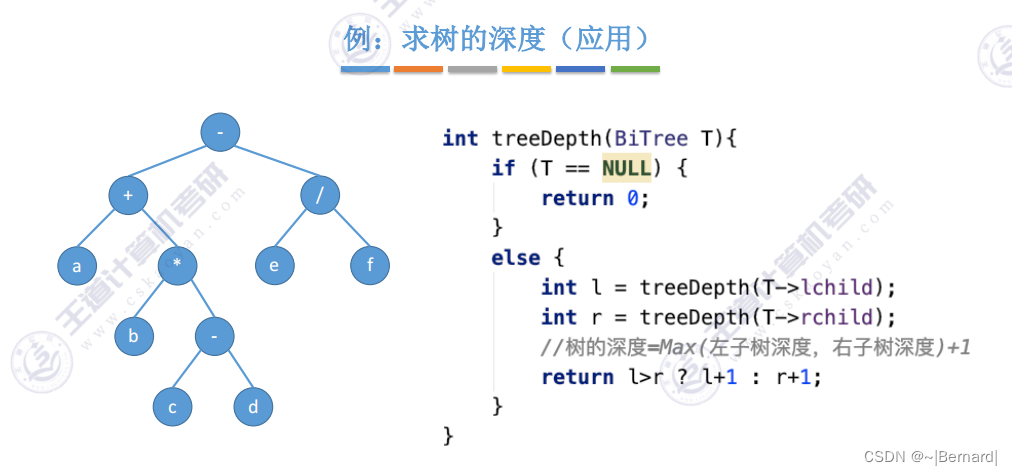
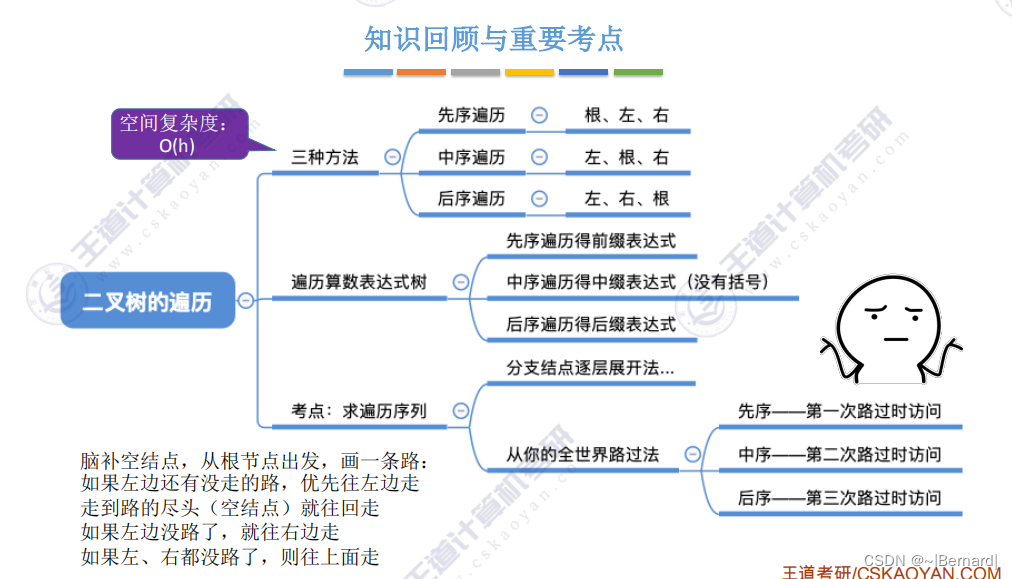
5.3.2 二叉树的层次遍历


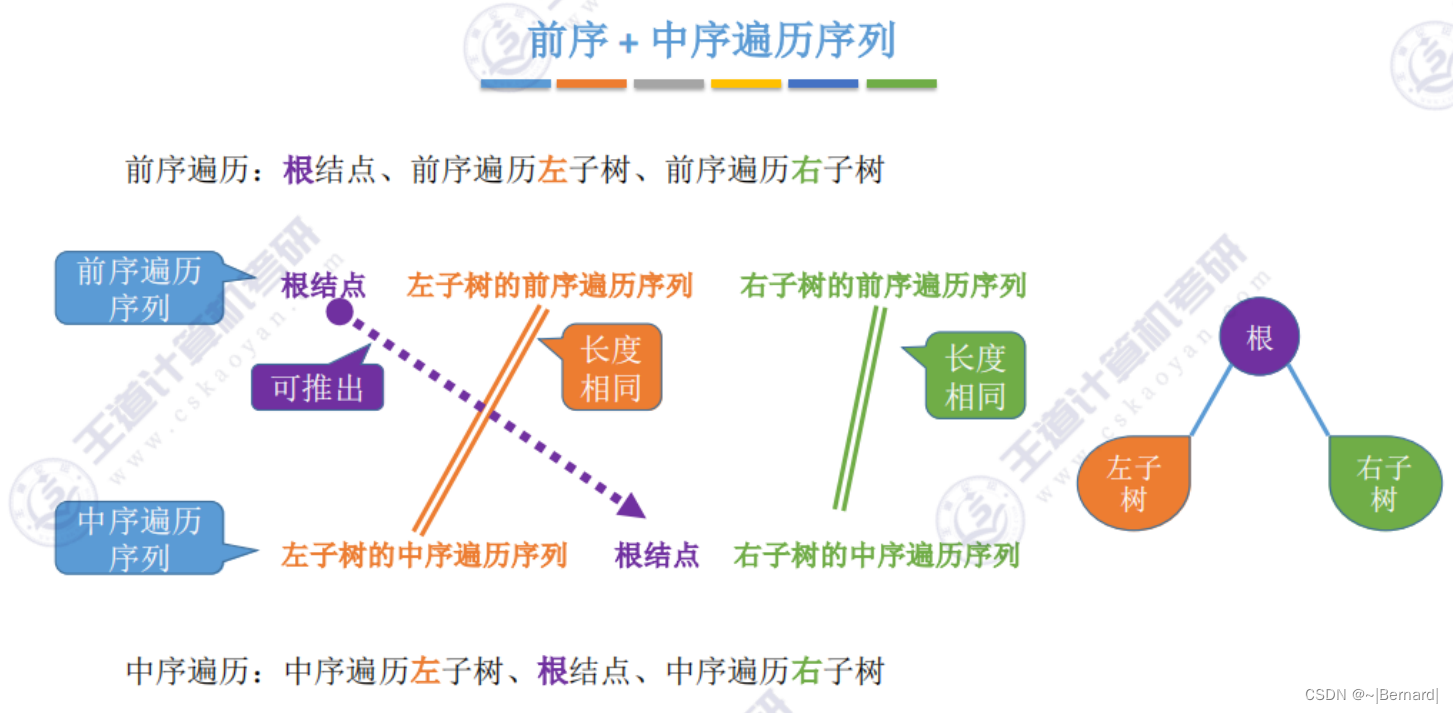
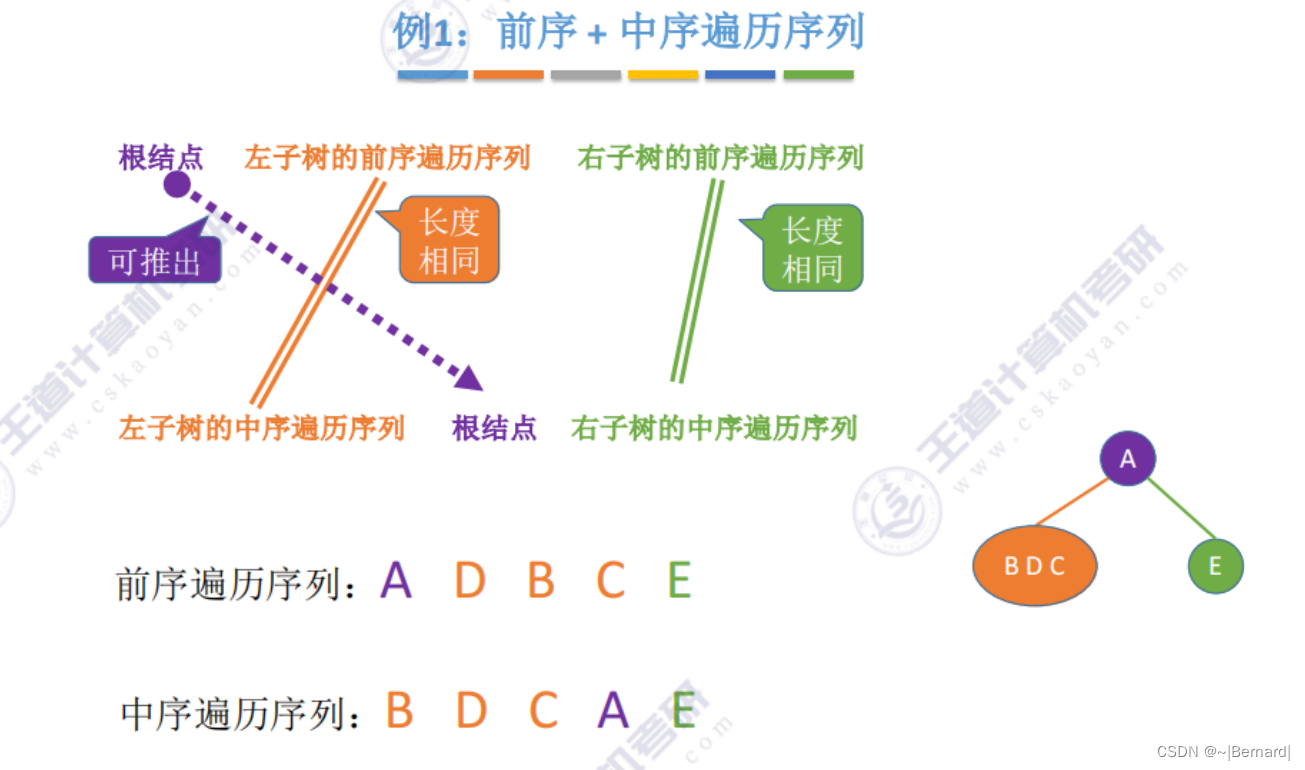
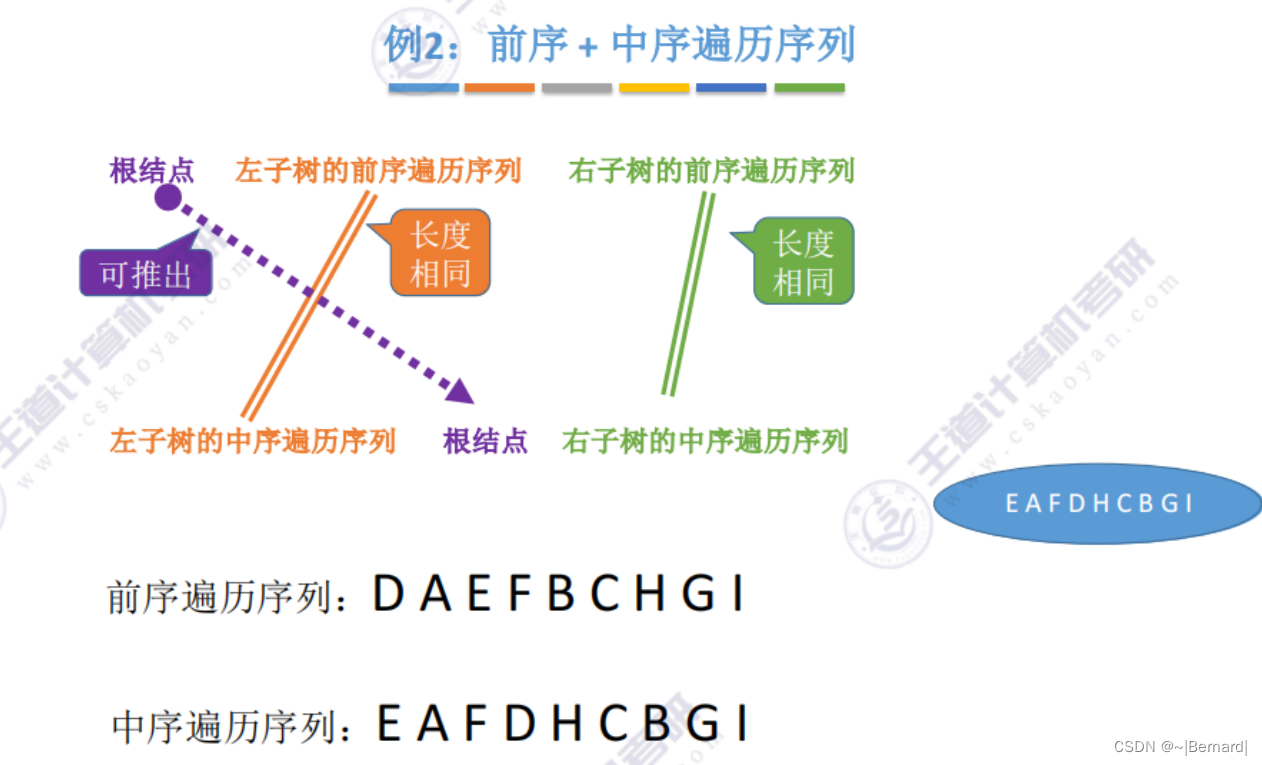
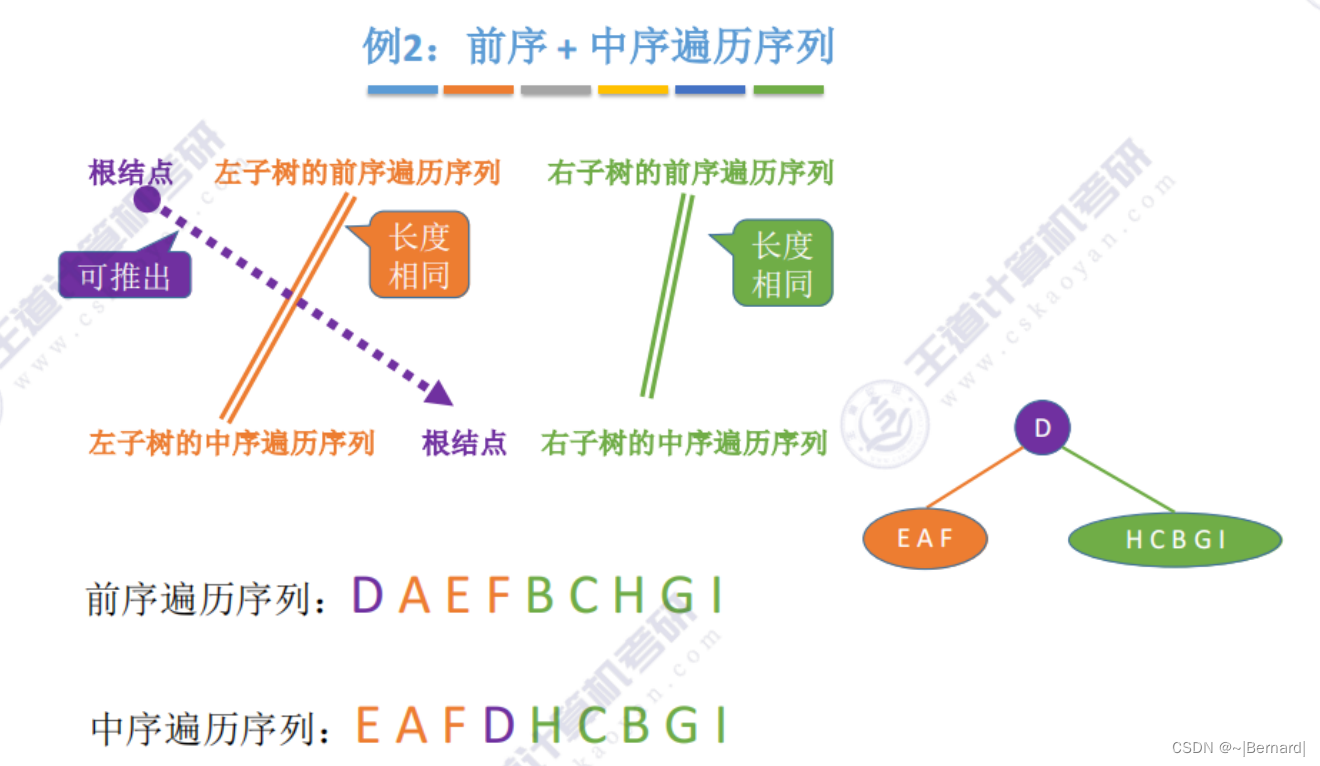
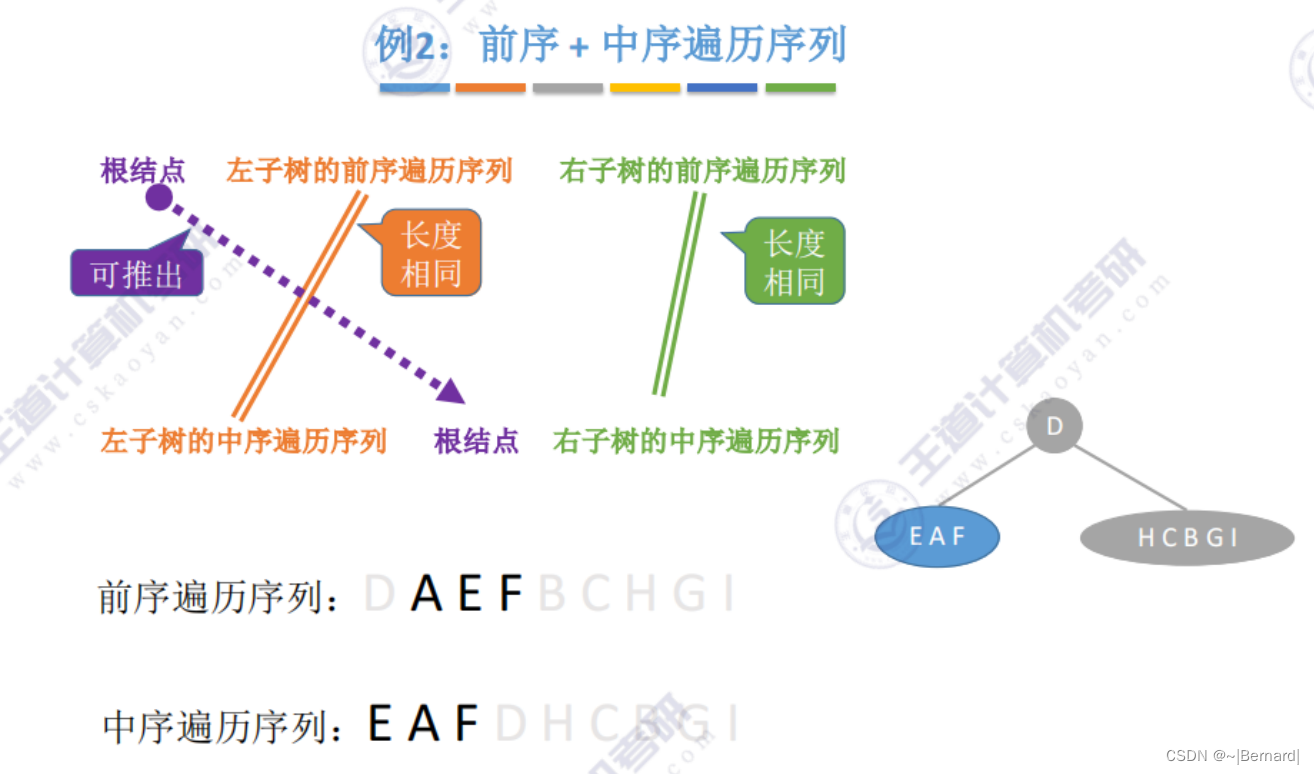
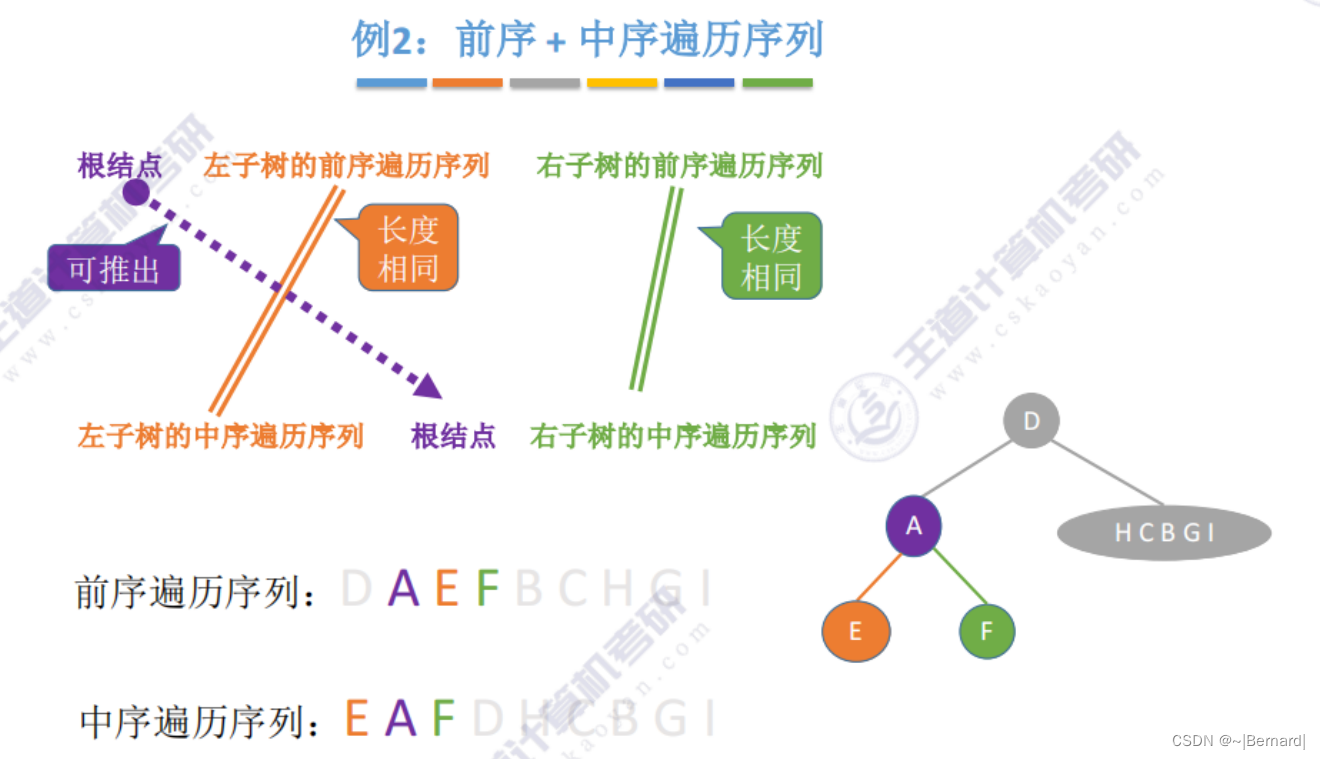
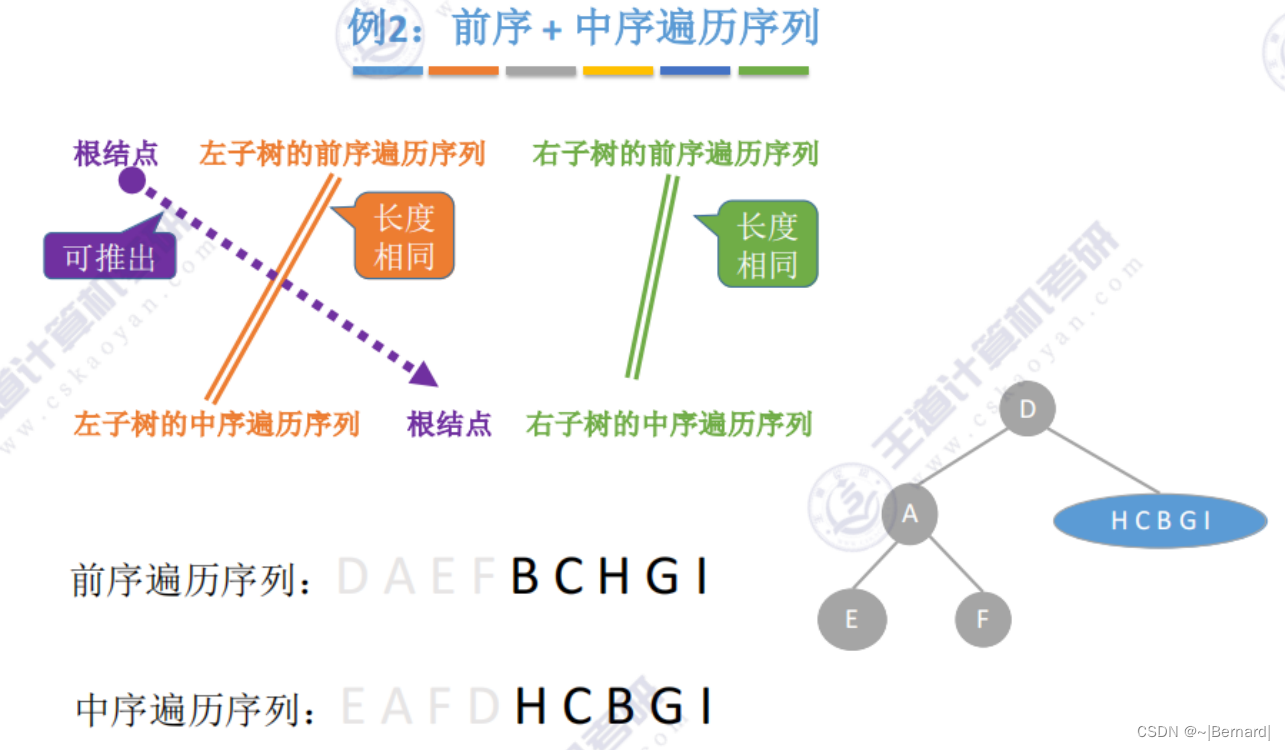
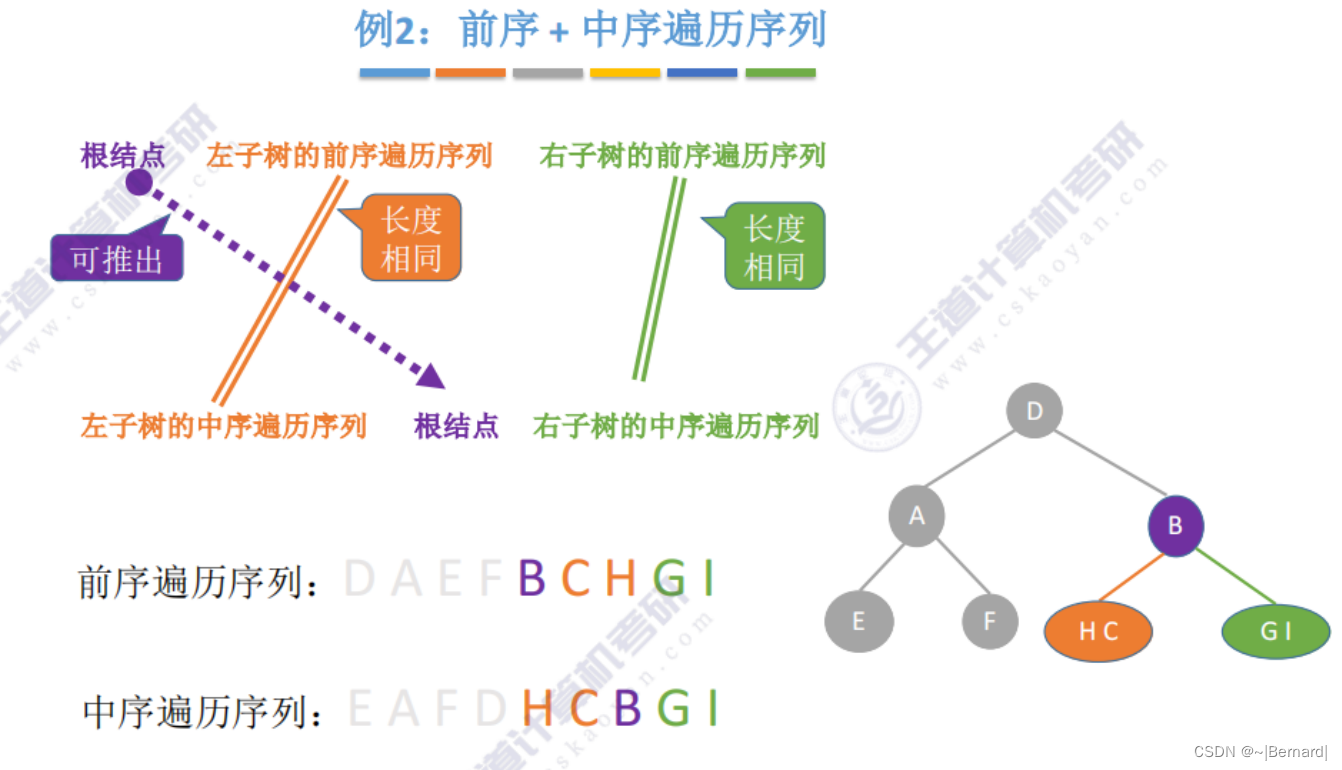
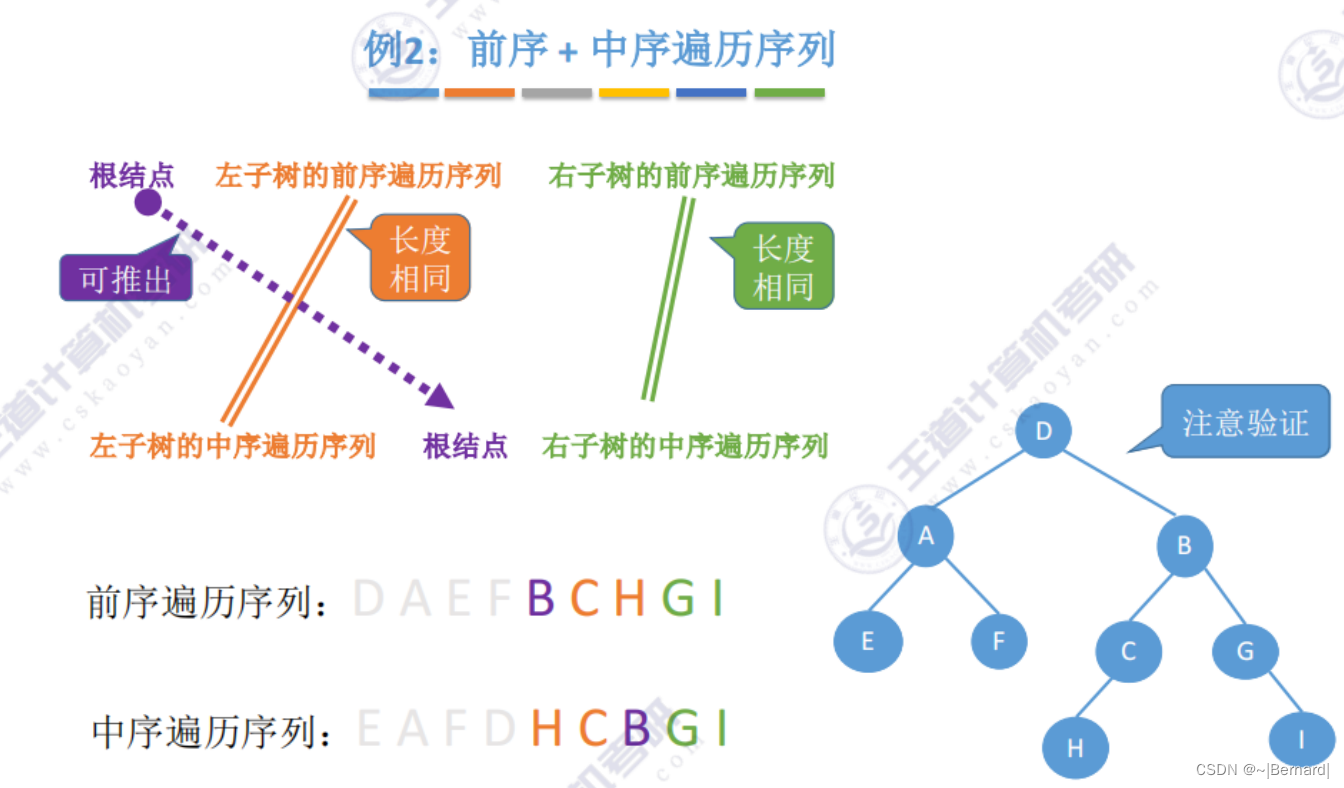
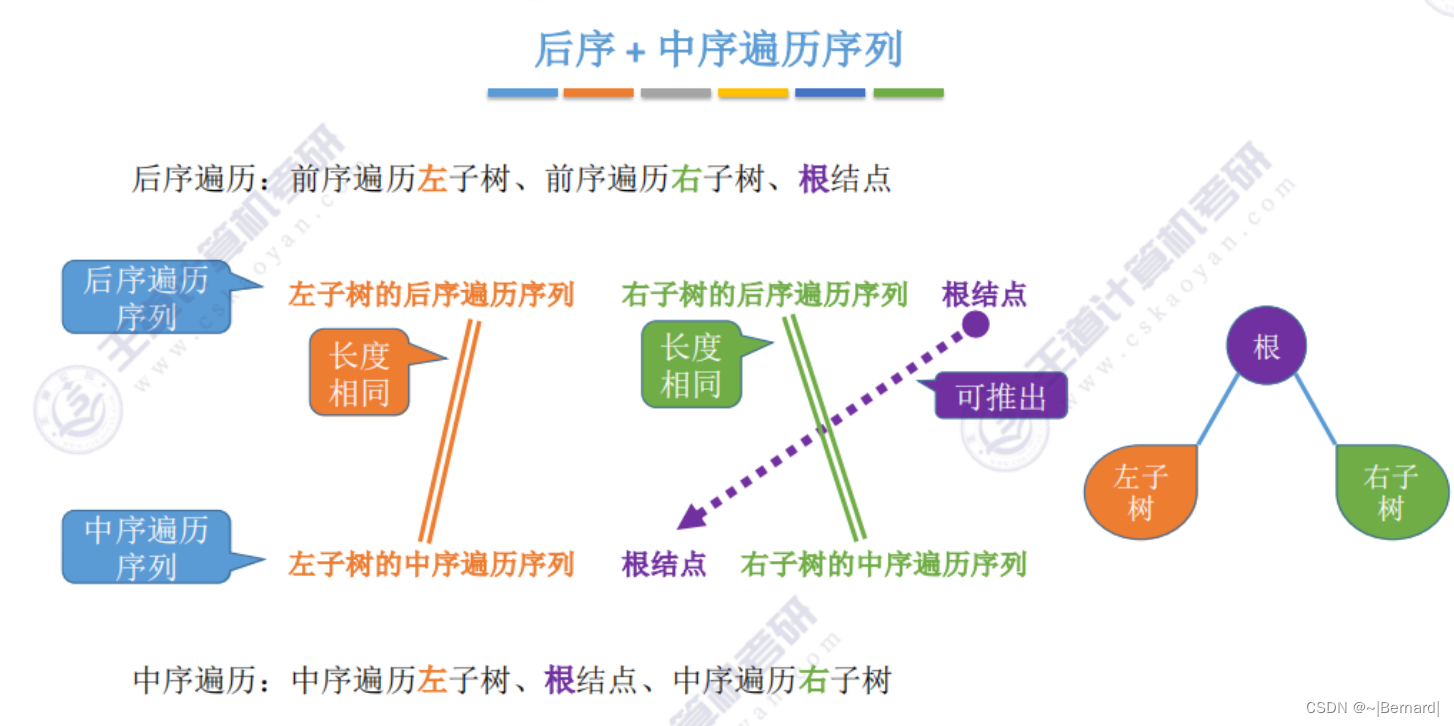
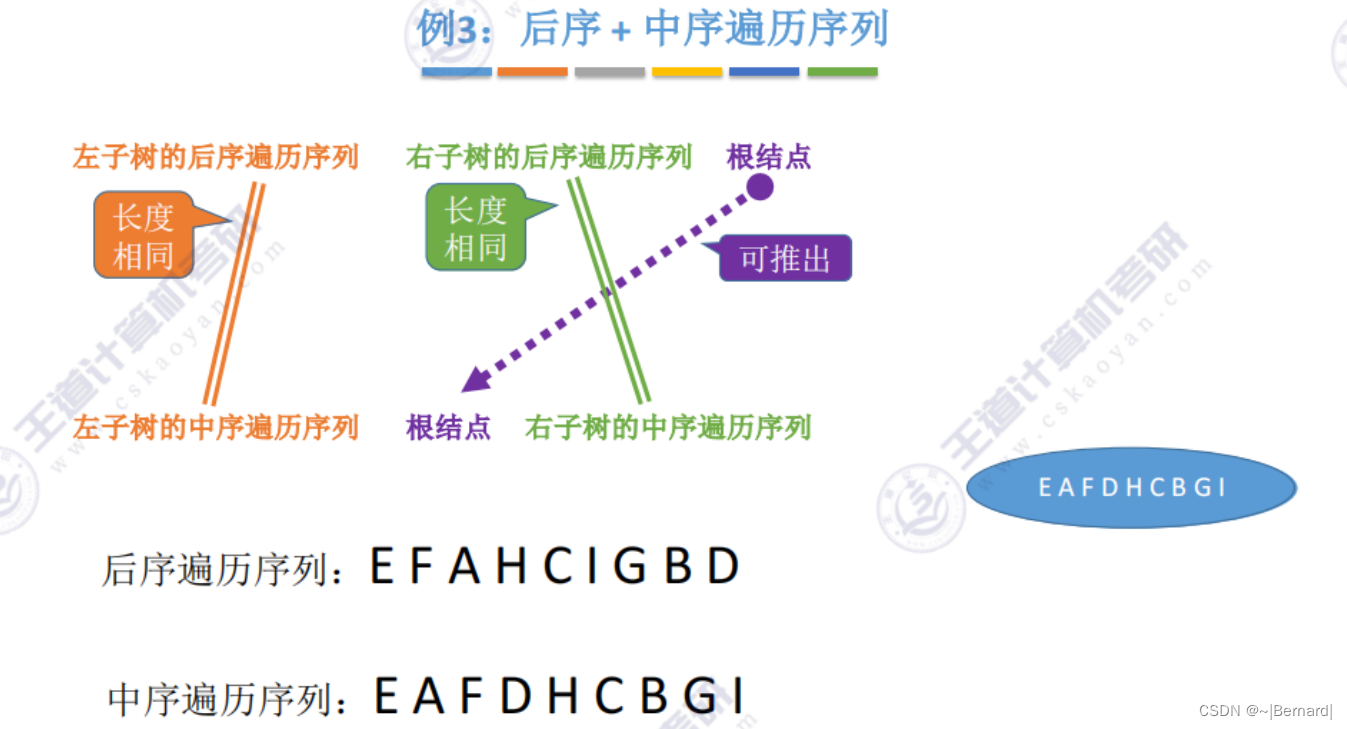
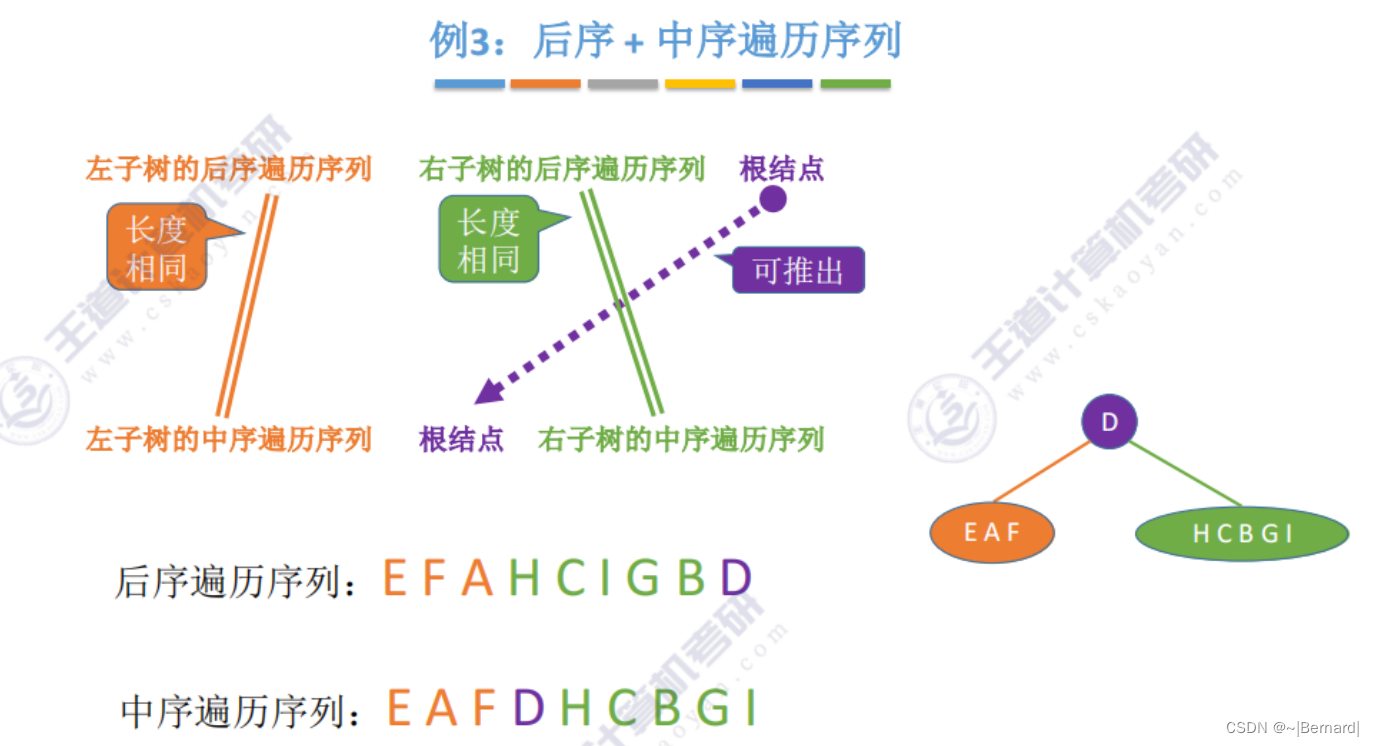
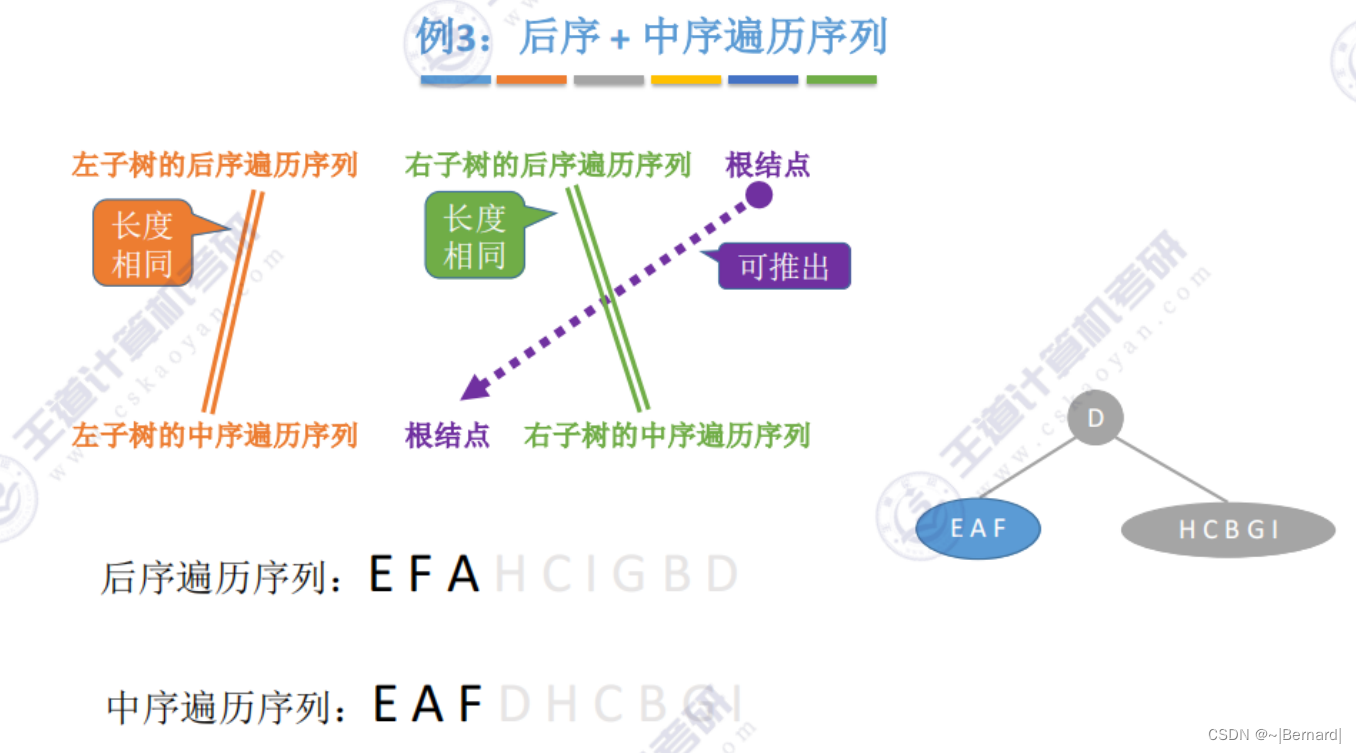
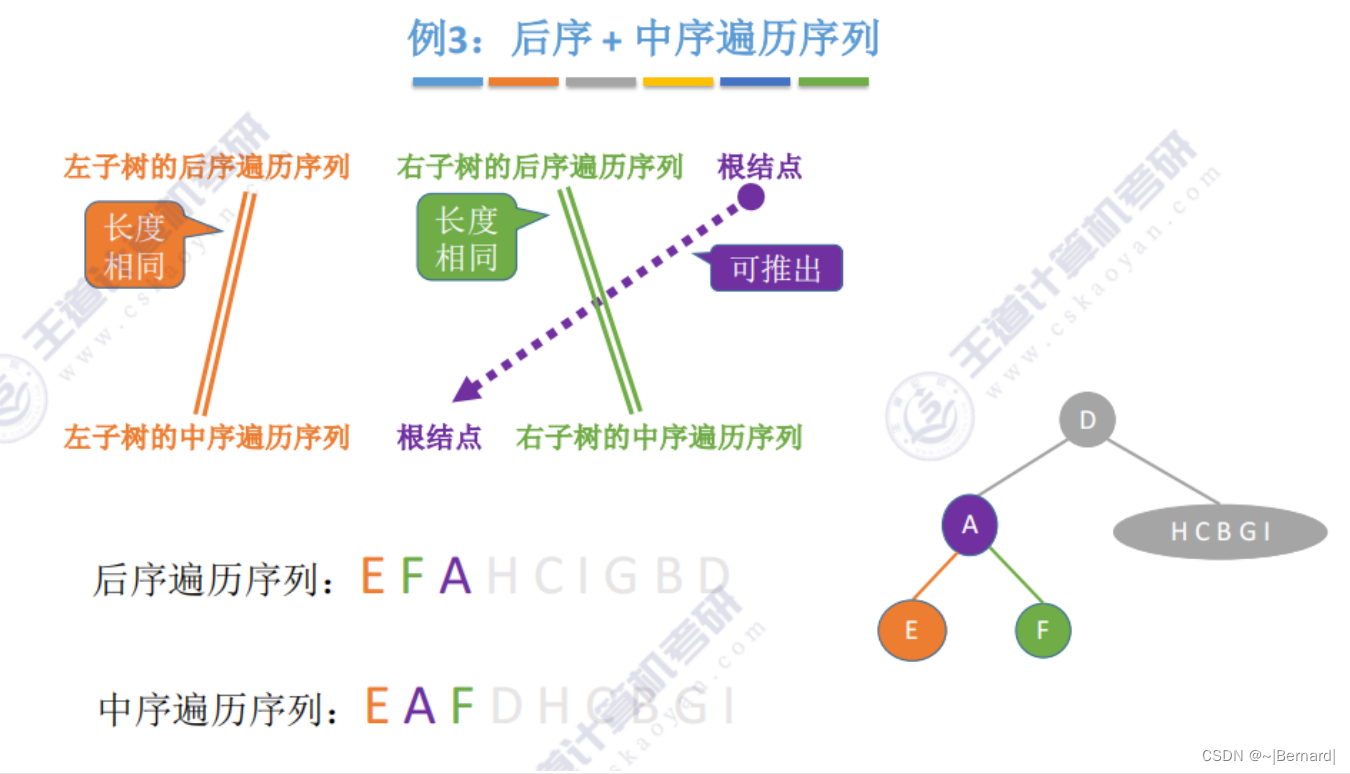
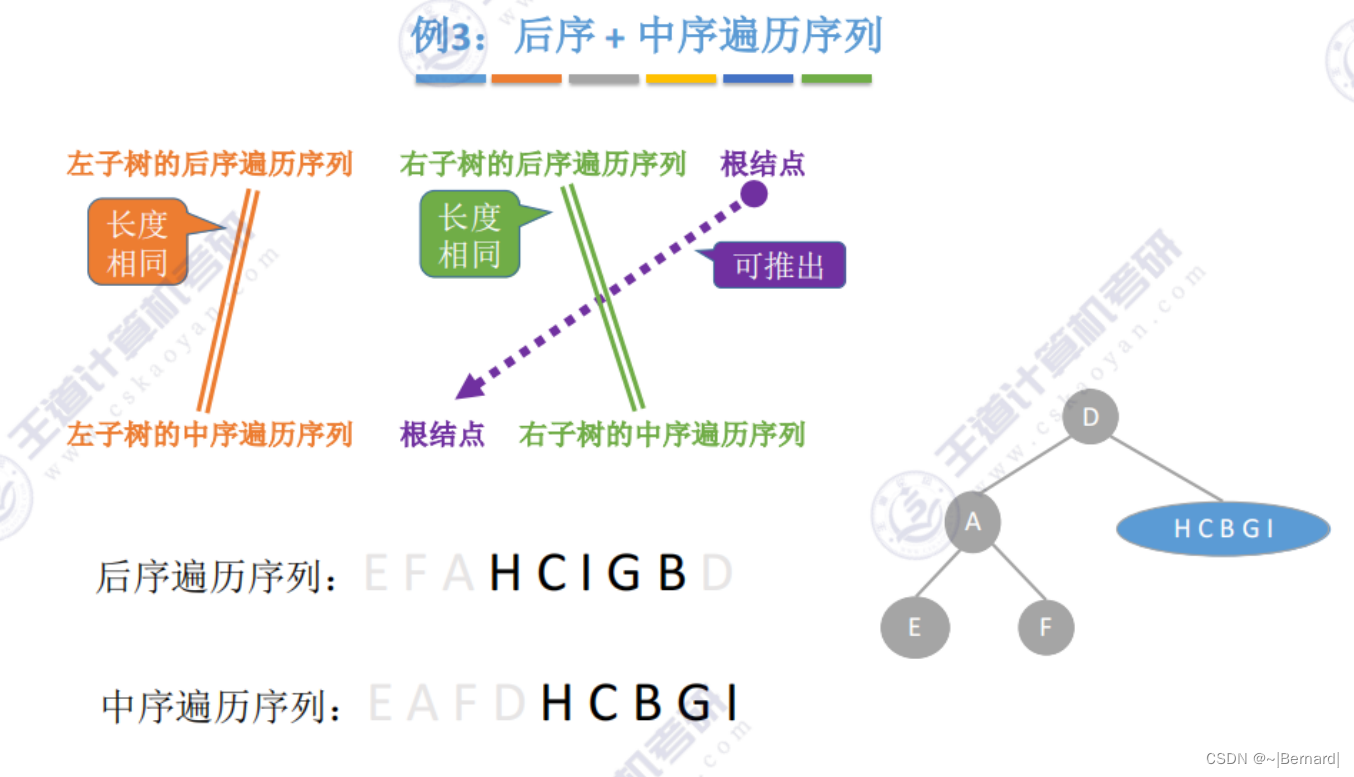
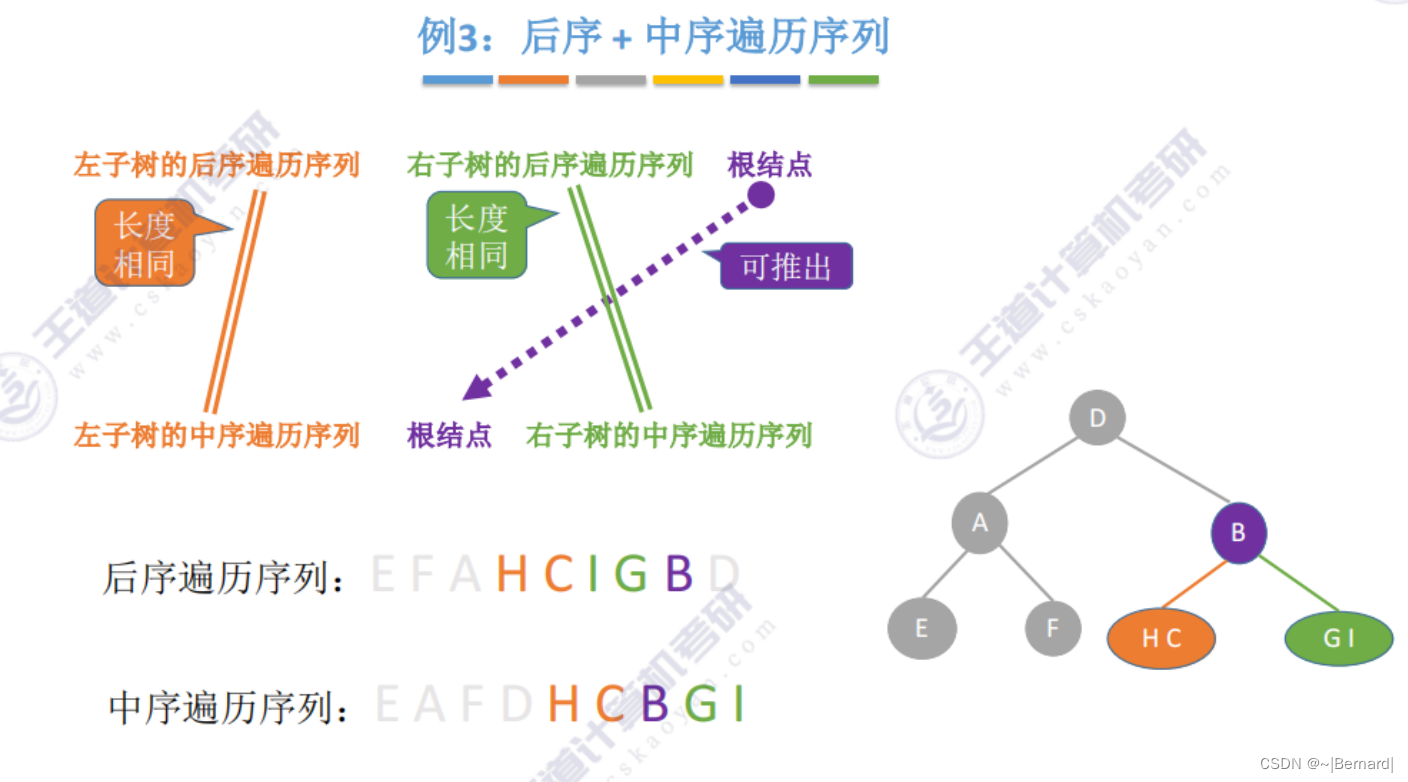
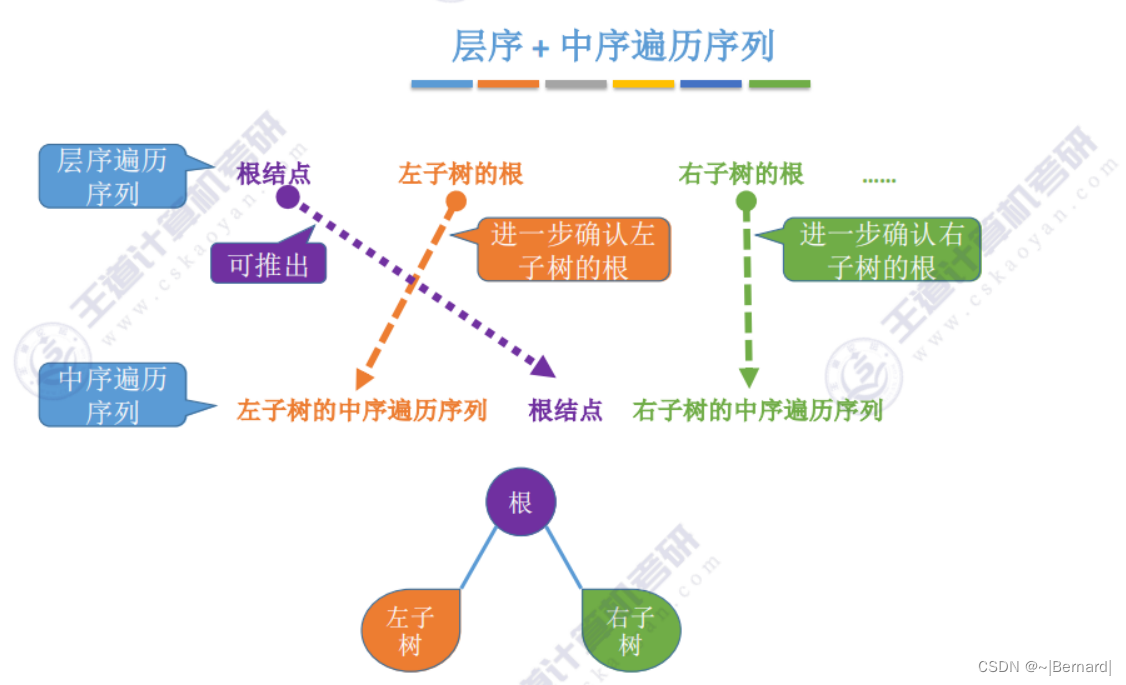
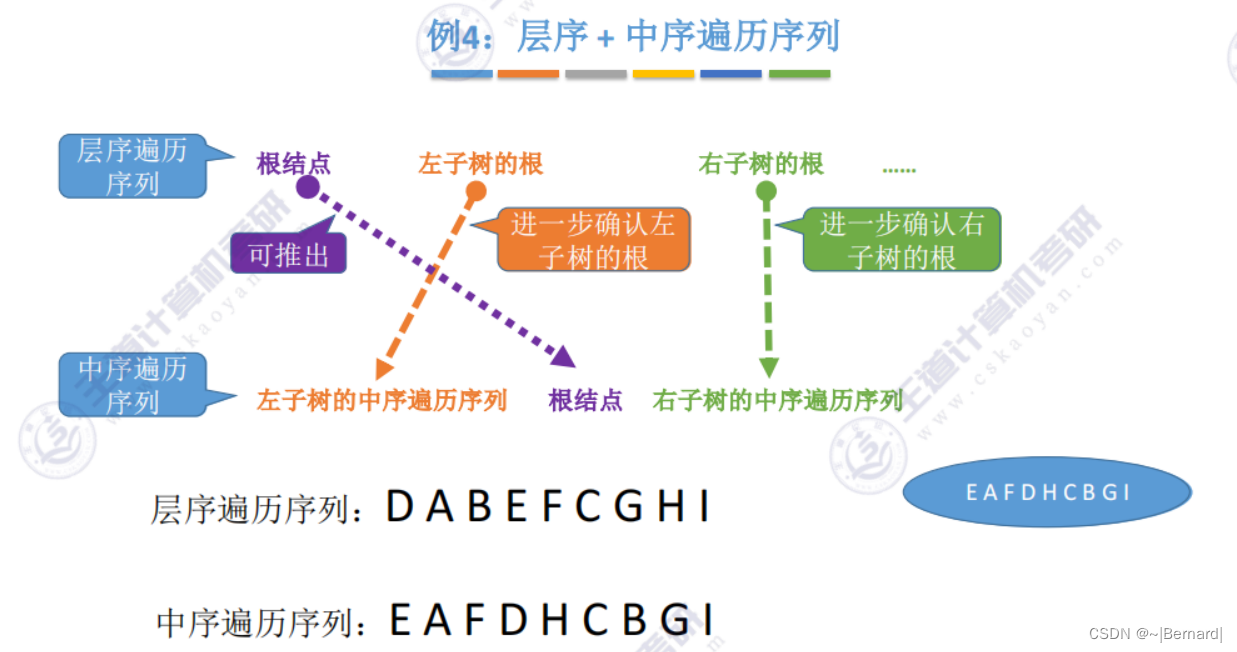
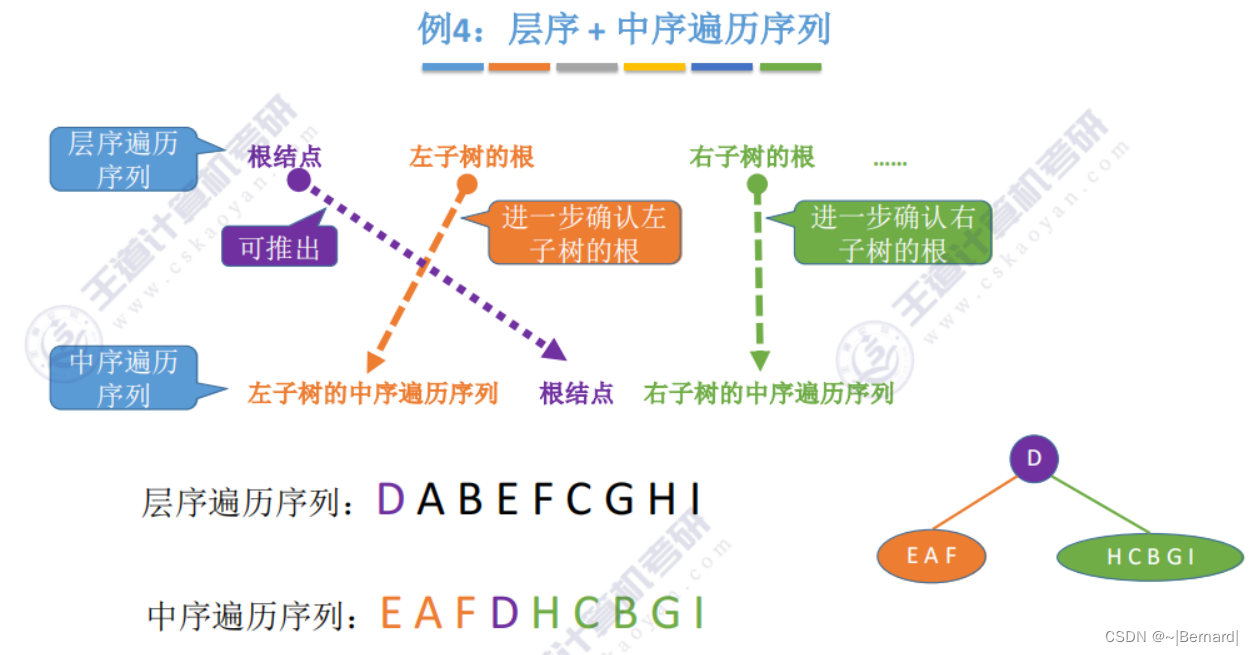
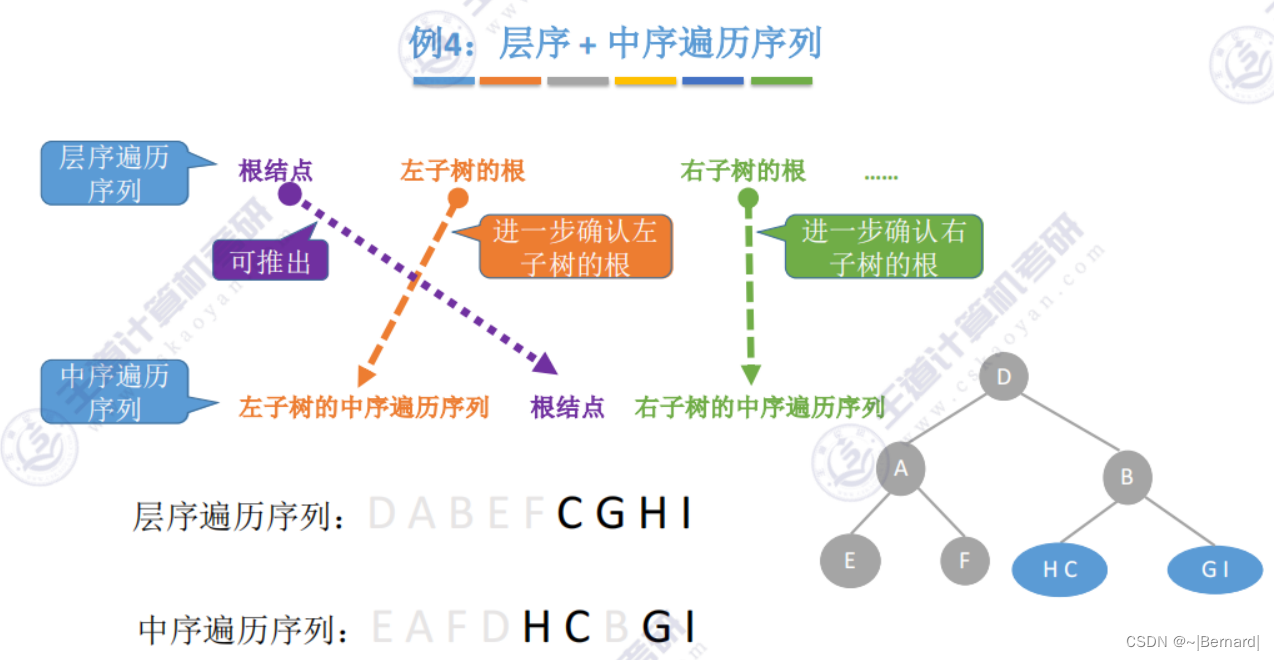
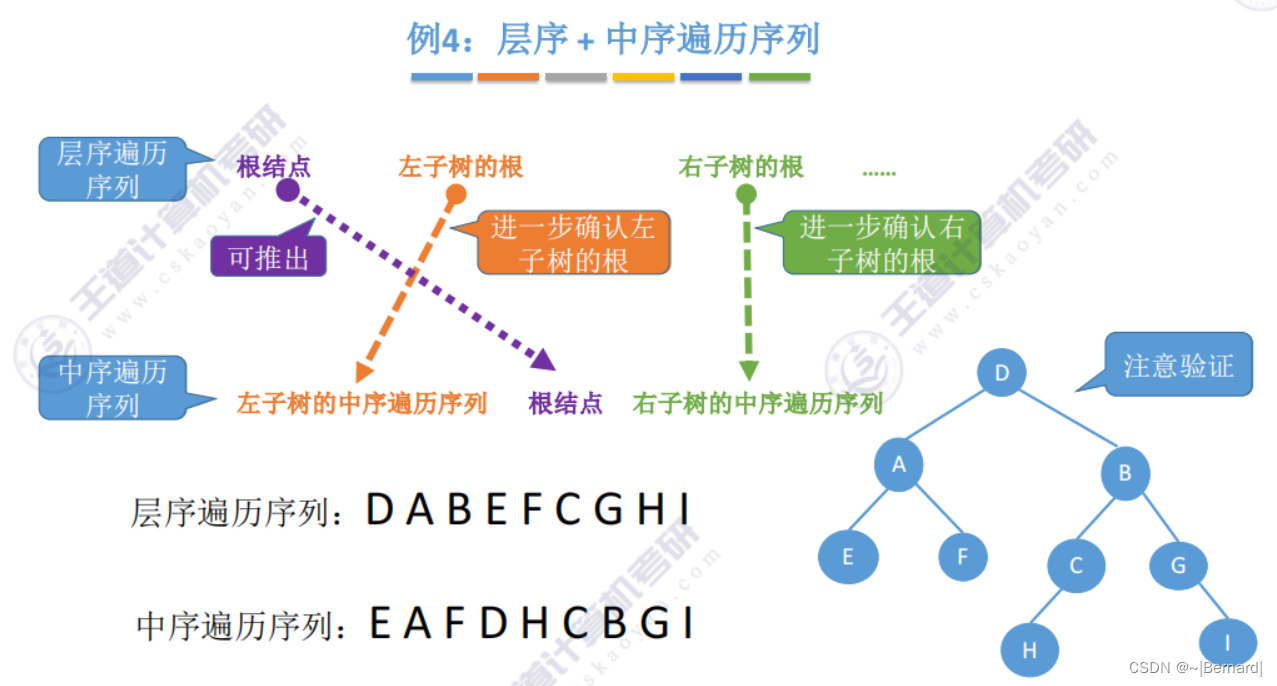
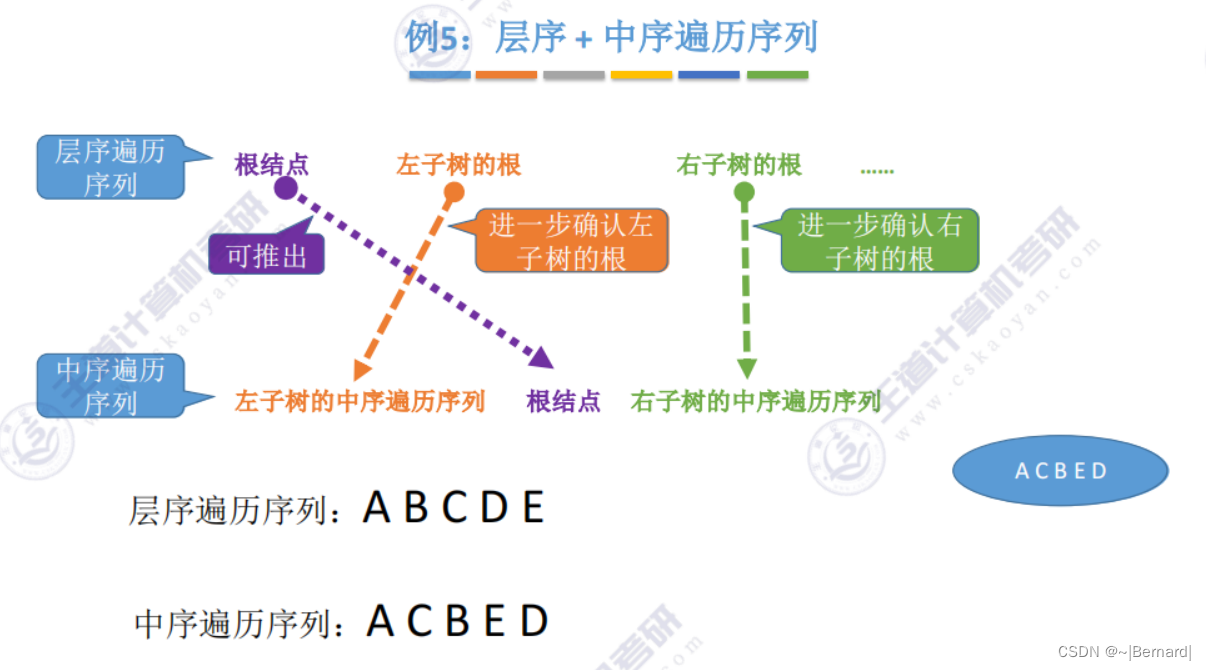
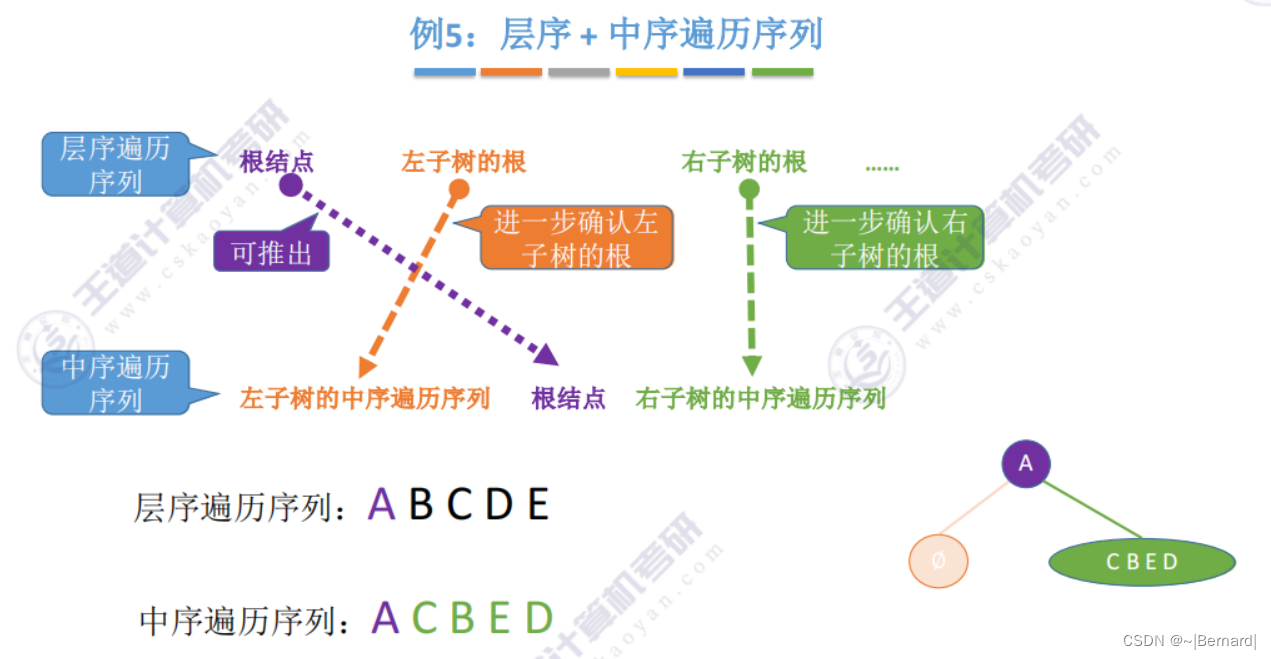
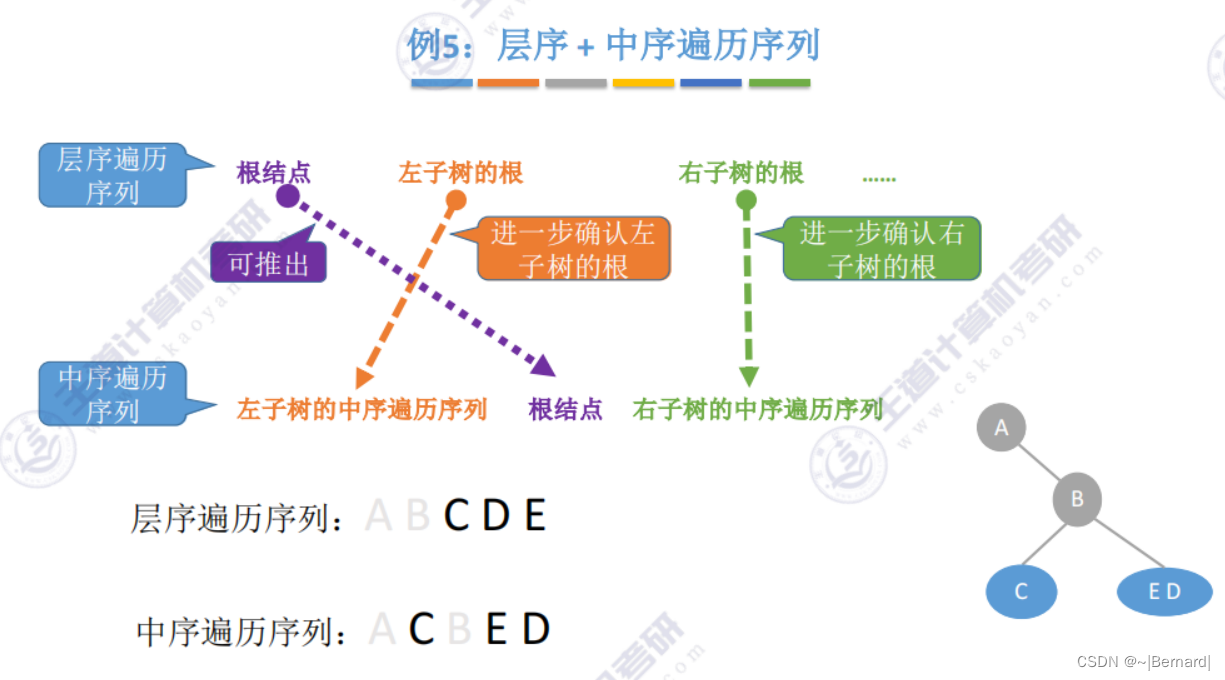
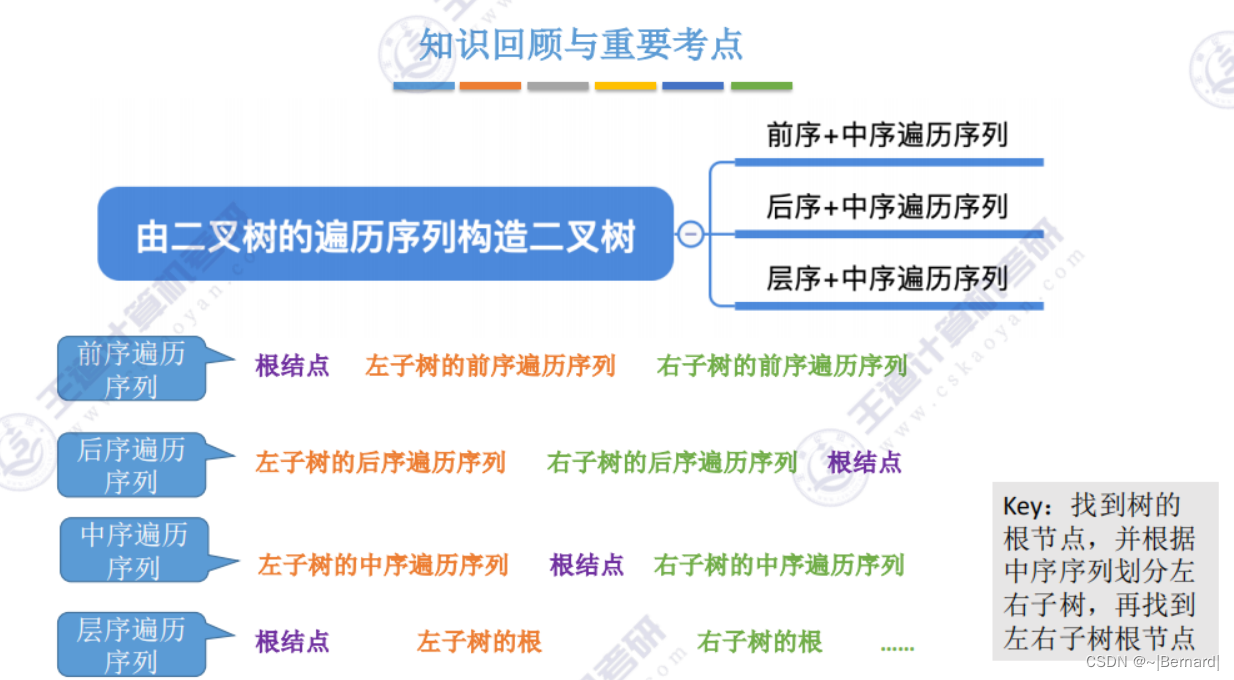
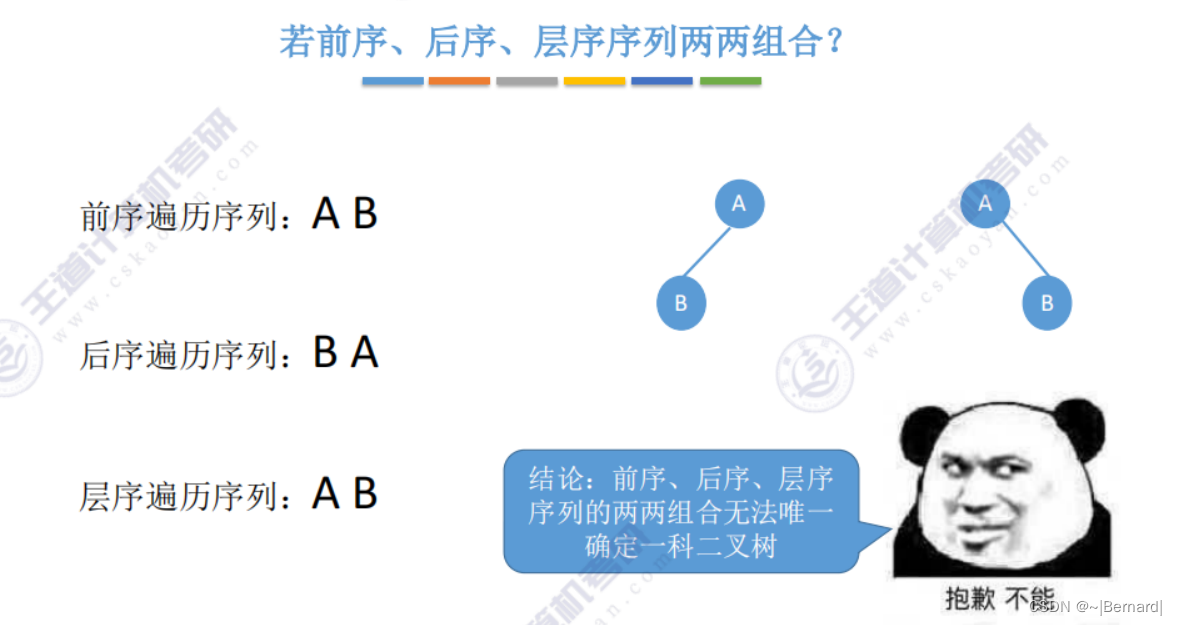
 5.3.3 由遍历序列构造二叉树
5.3.3 由遍历序列构造二叉树
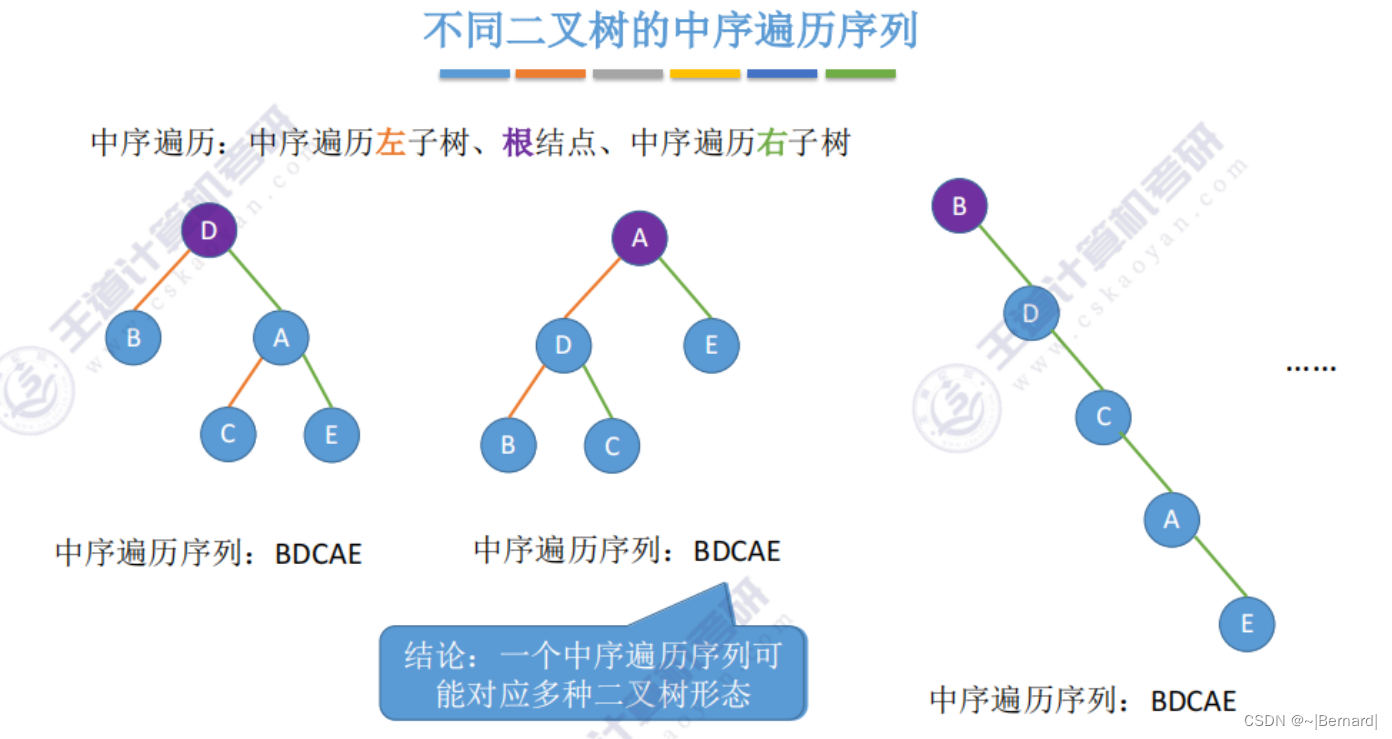
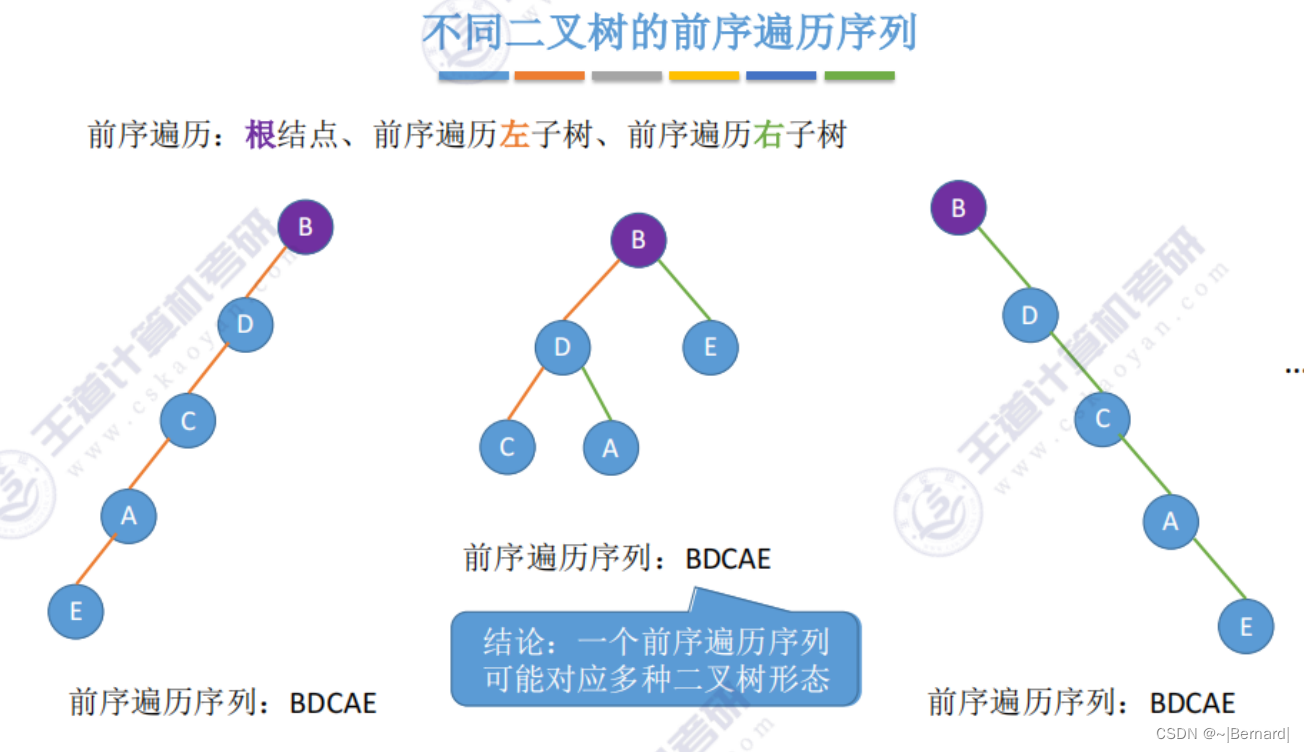
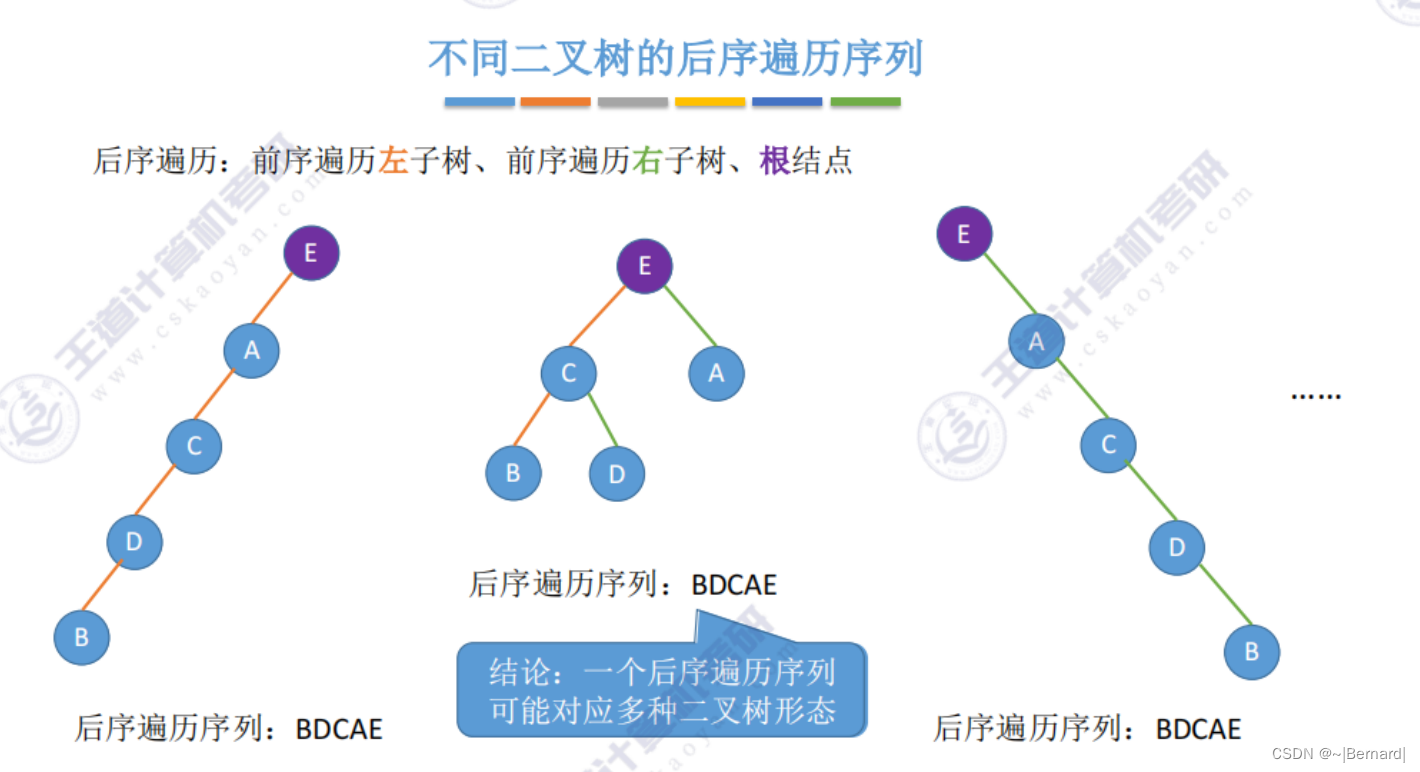
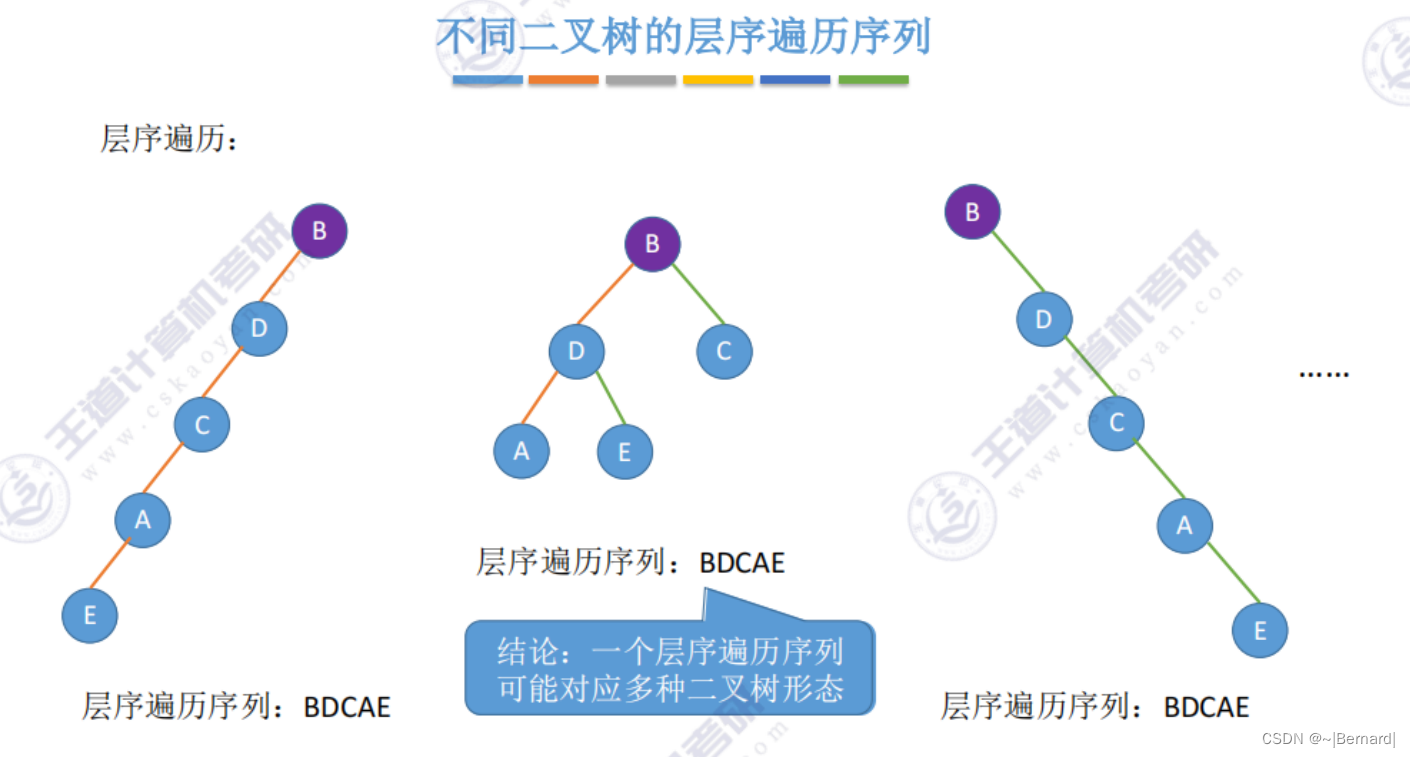
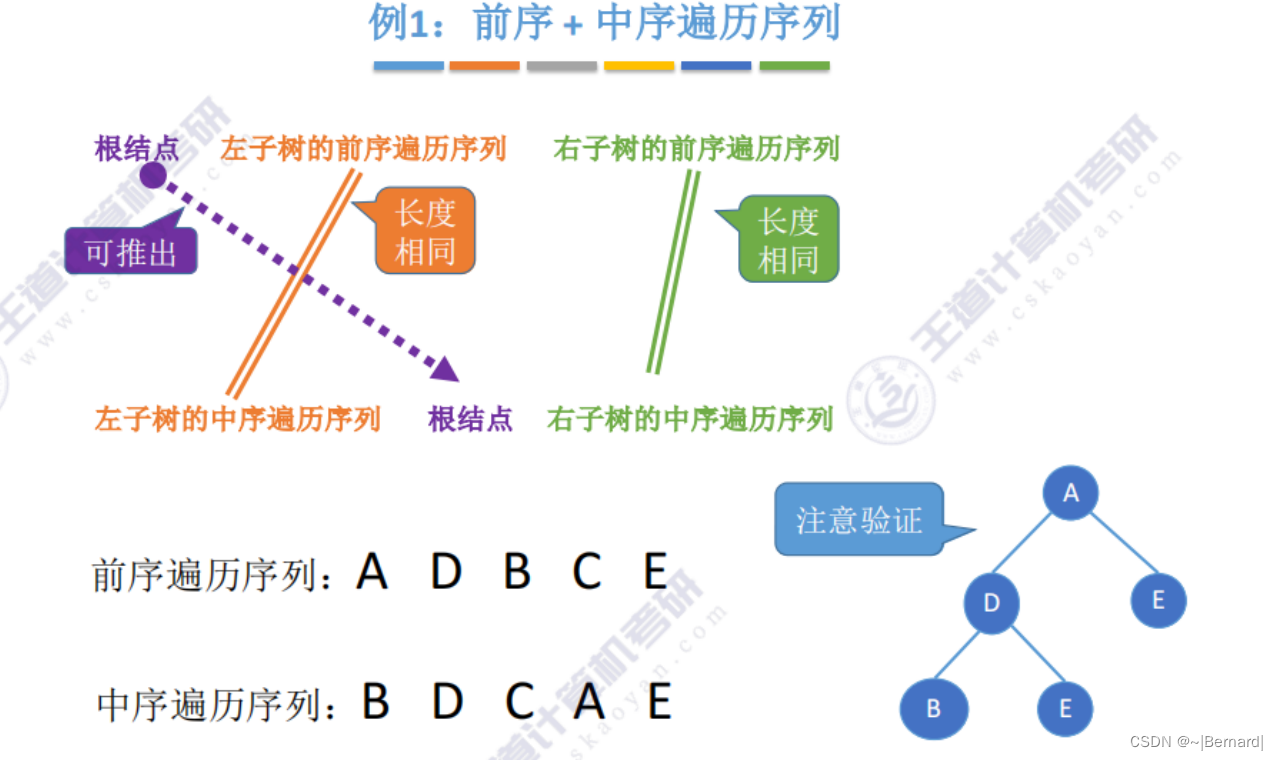
 注意:一定要有中序序列才可以推出一颗二叉树的完整形态
注意:一定要有中序序列才可以推出一颗二叉树的完整形态




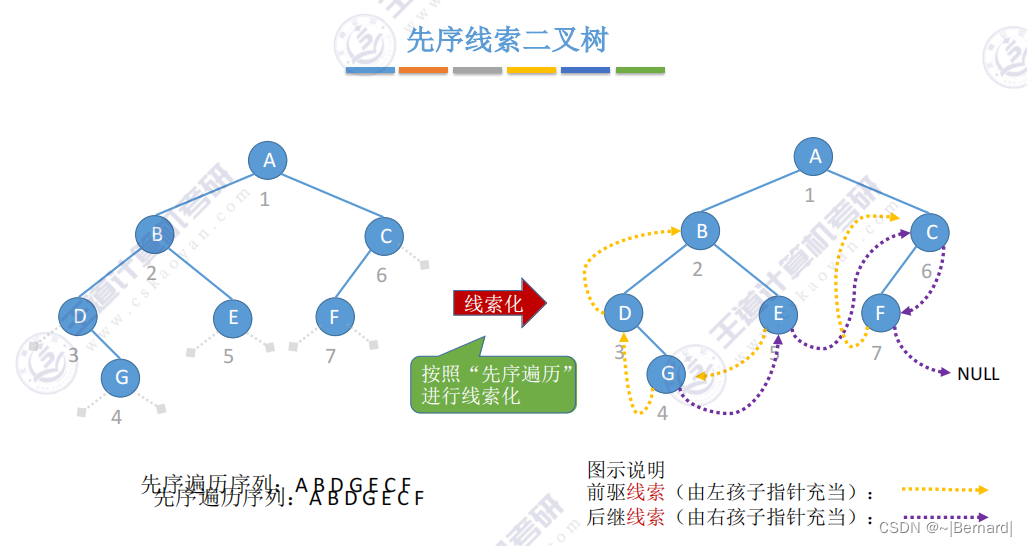
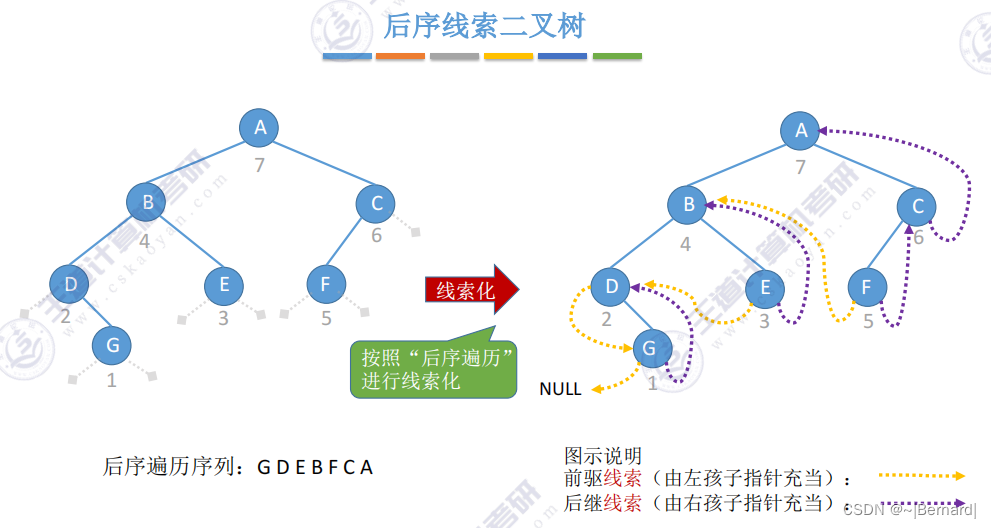
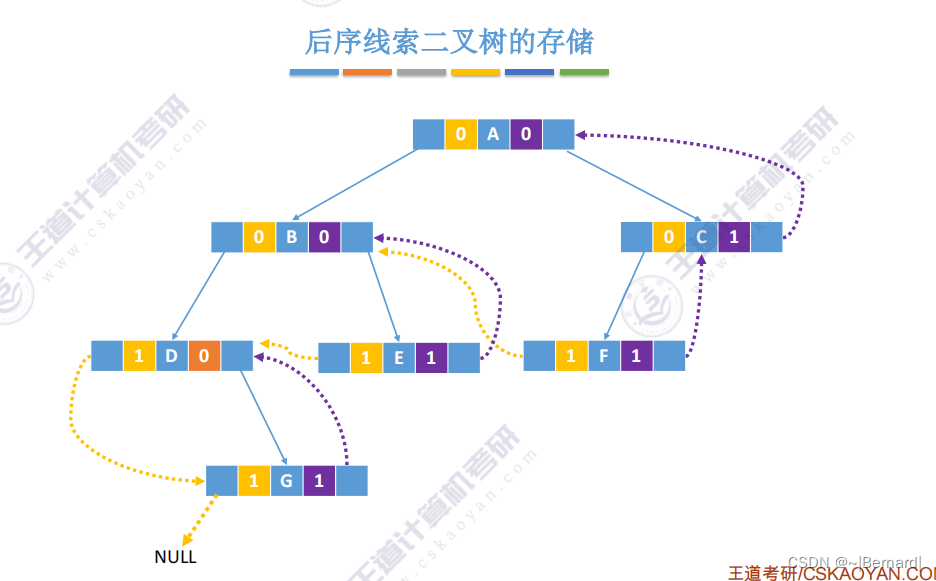
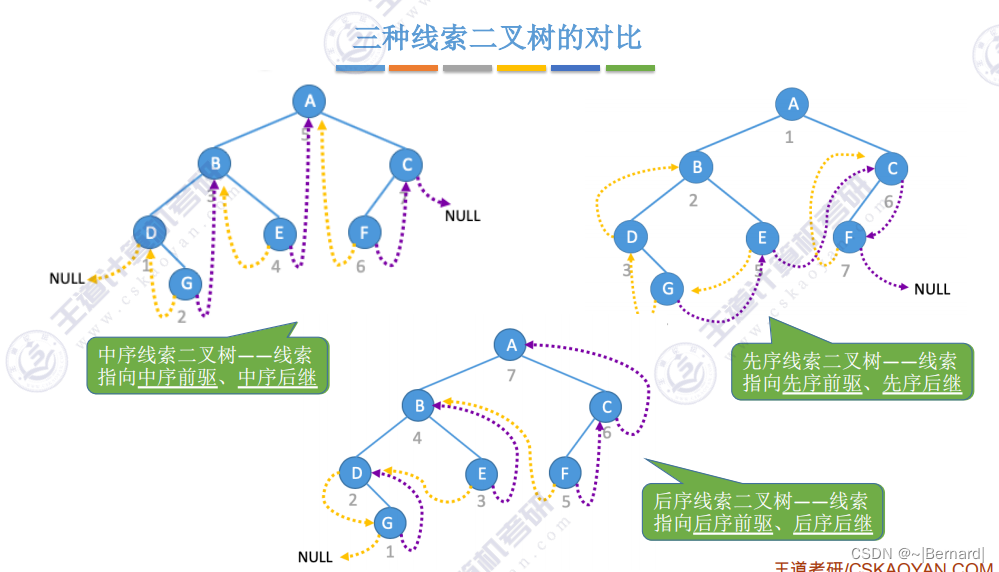
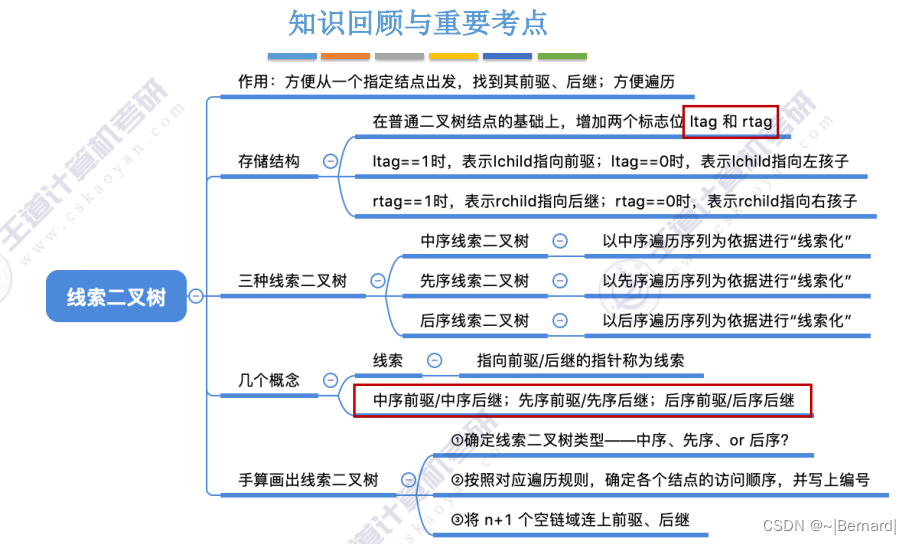
 5.3.4 线索二叉树的概念
5.3.4 线索二叉树的概念
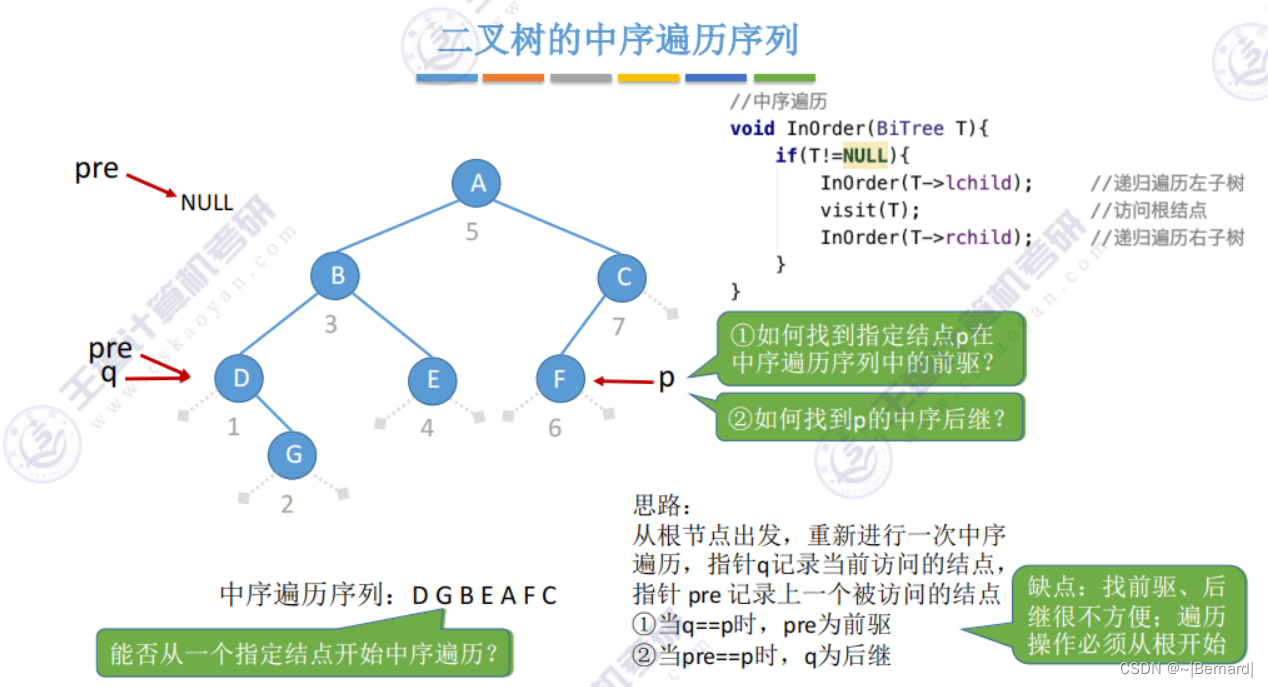
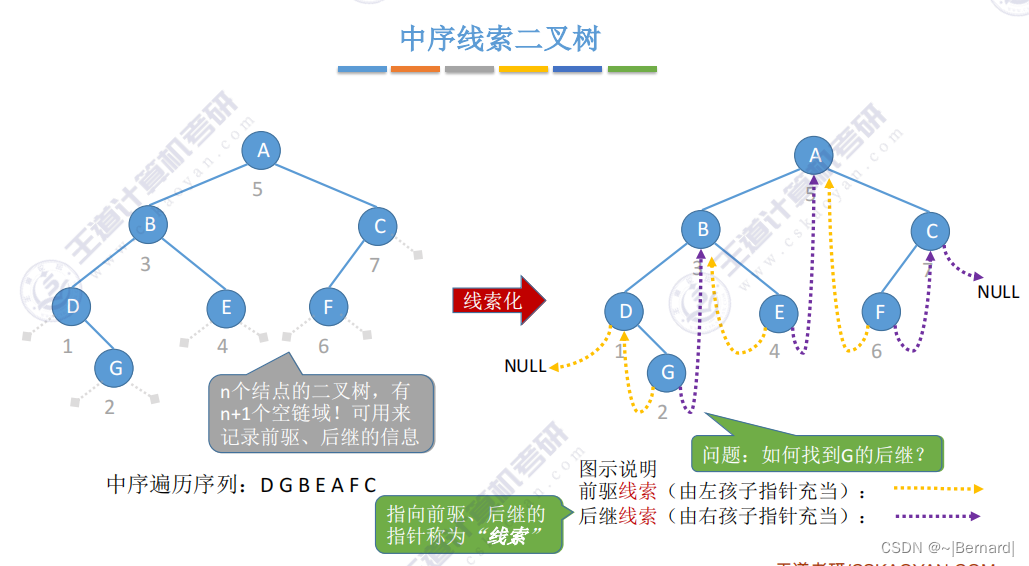 注意:这里的前驱和后继是基于先序遍历的结果的前驱和后期。而此前的前驱和后继是基于节点。
注意:这里的前驱和后继是基于先序遍历的结果的前驱和后期。而此前的前驱和后继是基于节点。
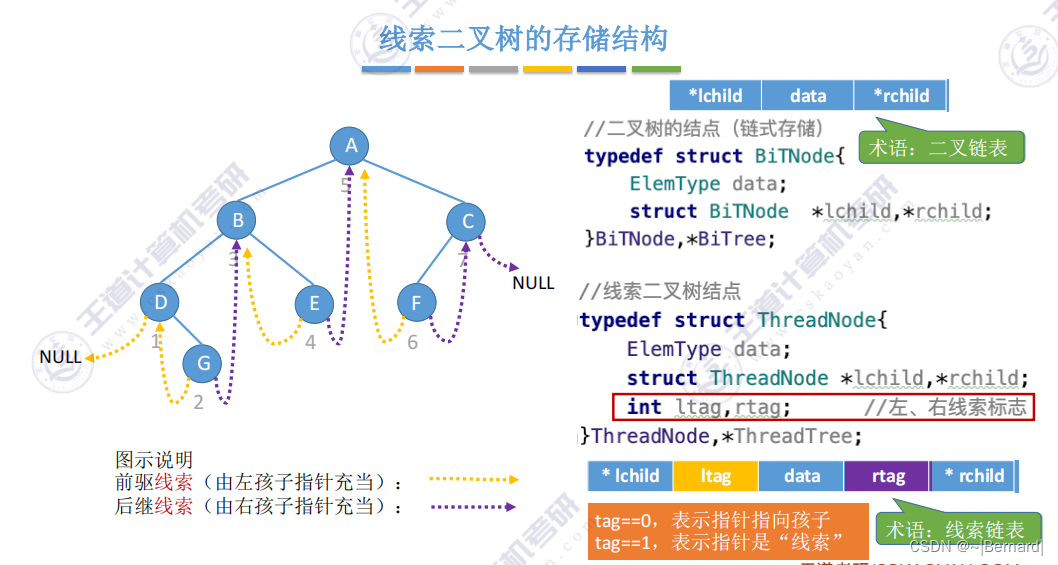
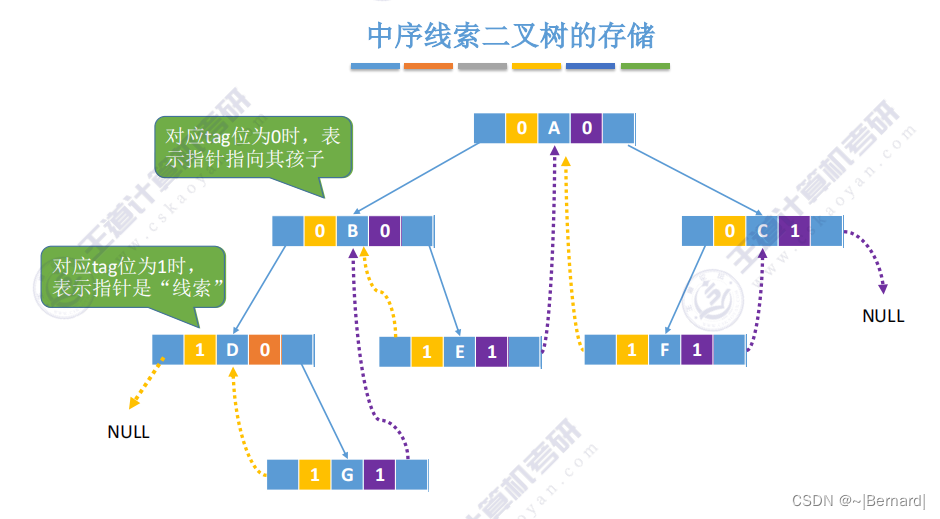

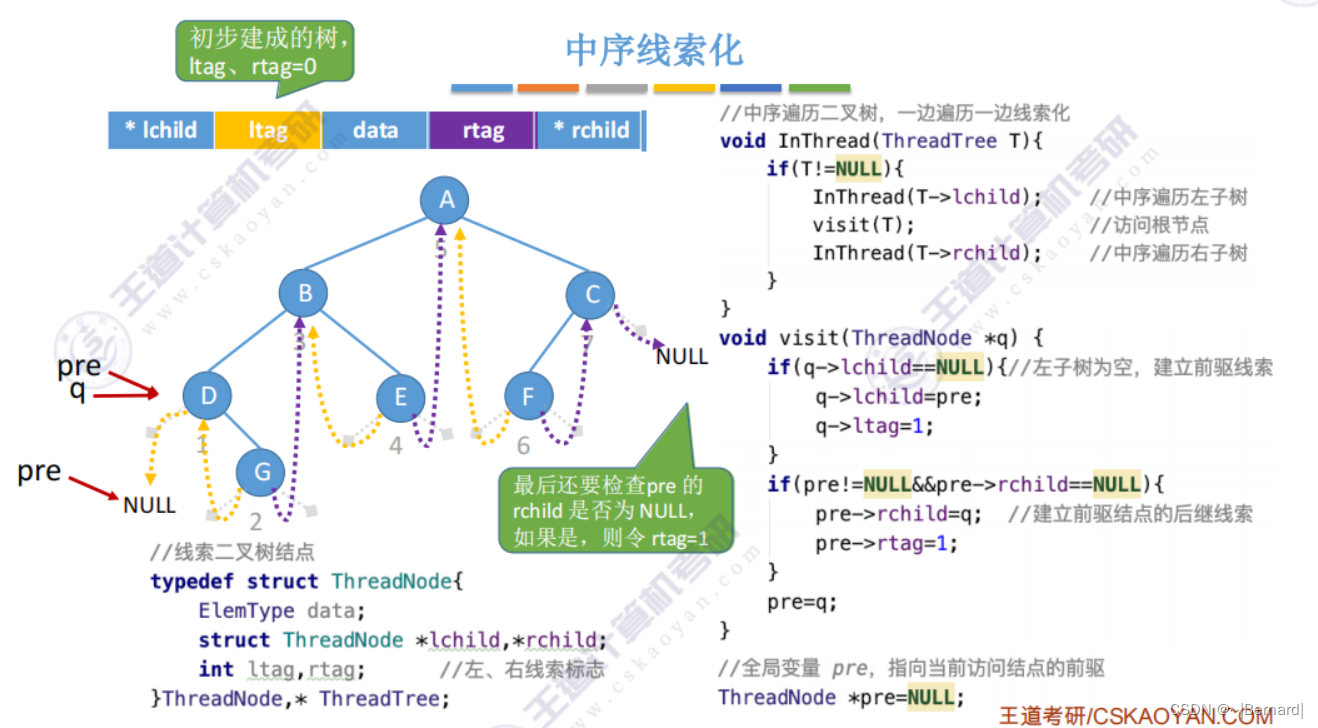
 5.3.5 二叉树的线索化
5.3.5 二叉树的线索化
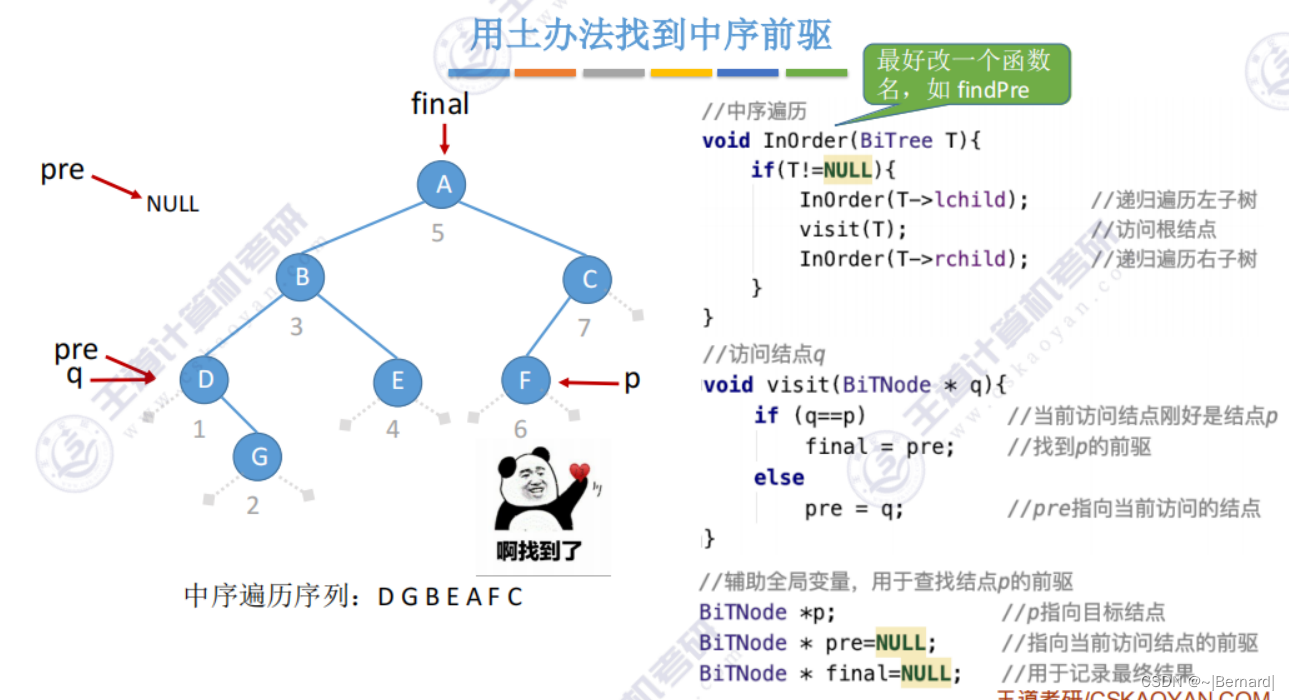

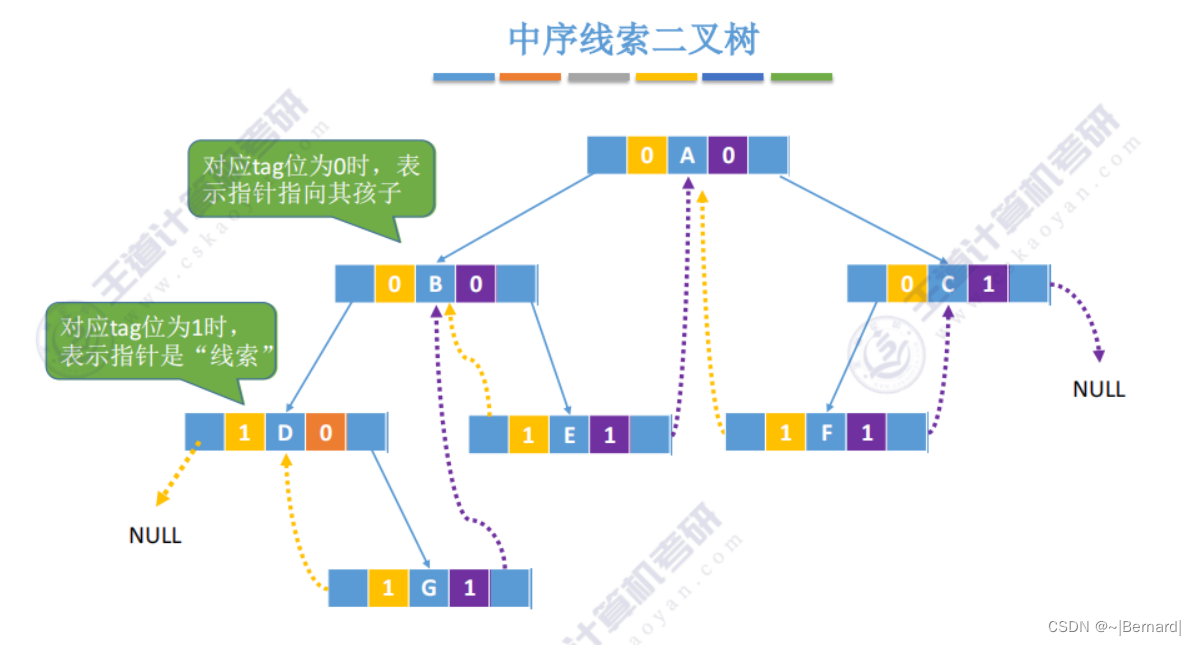






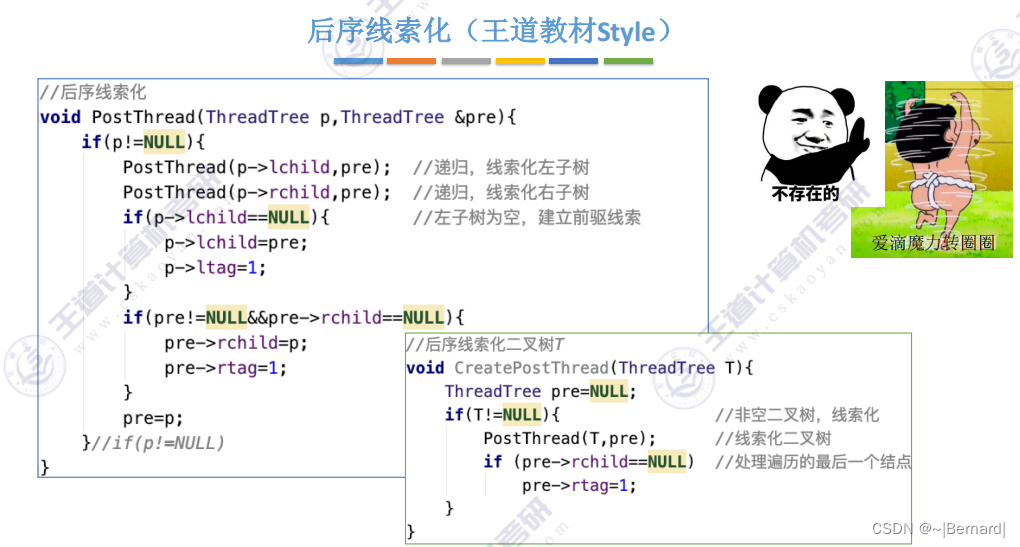
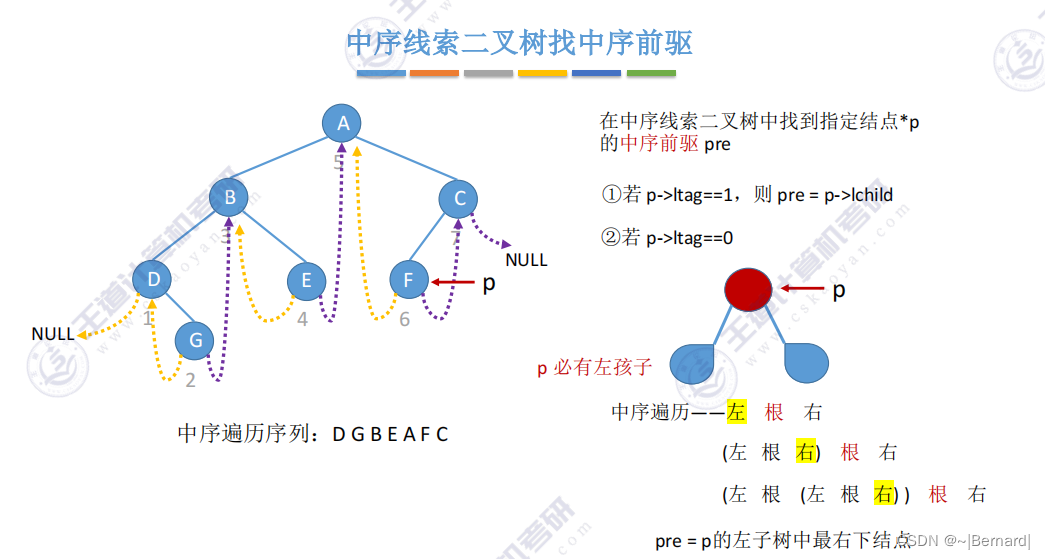
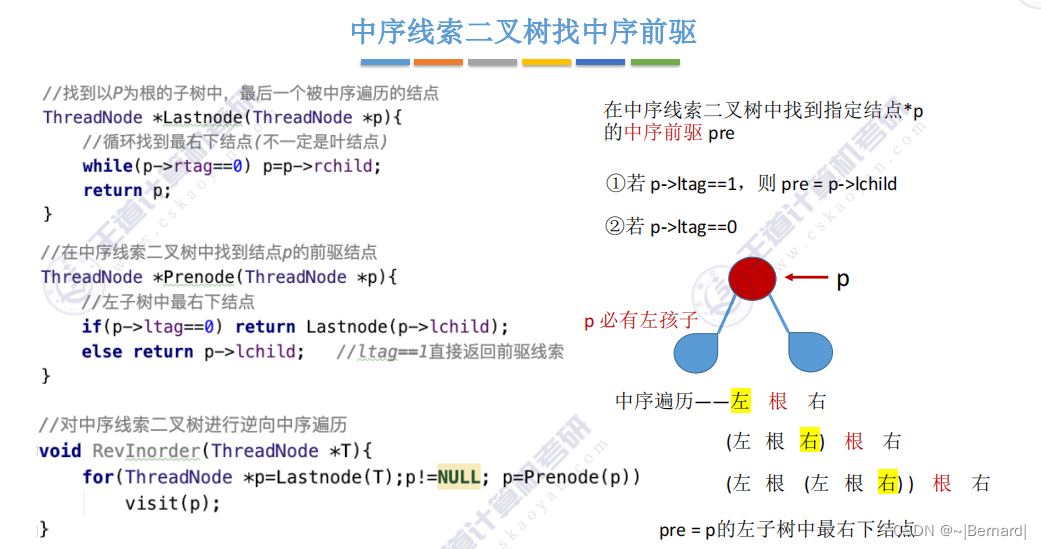
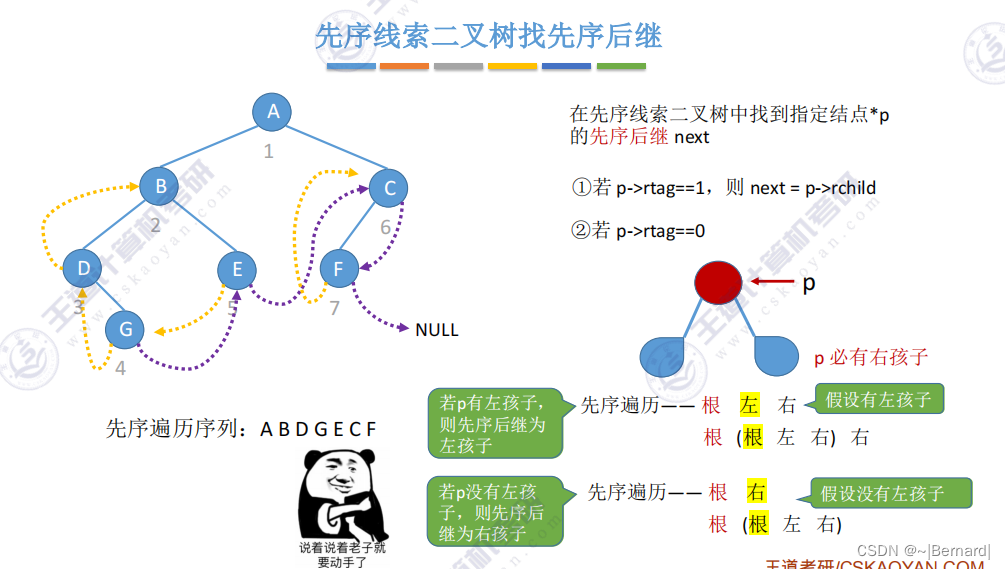
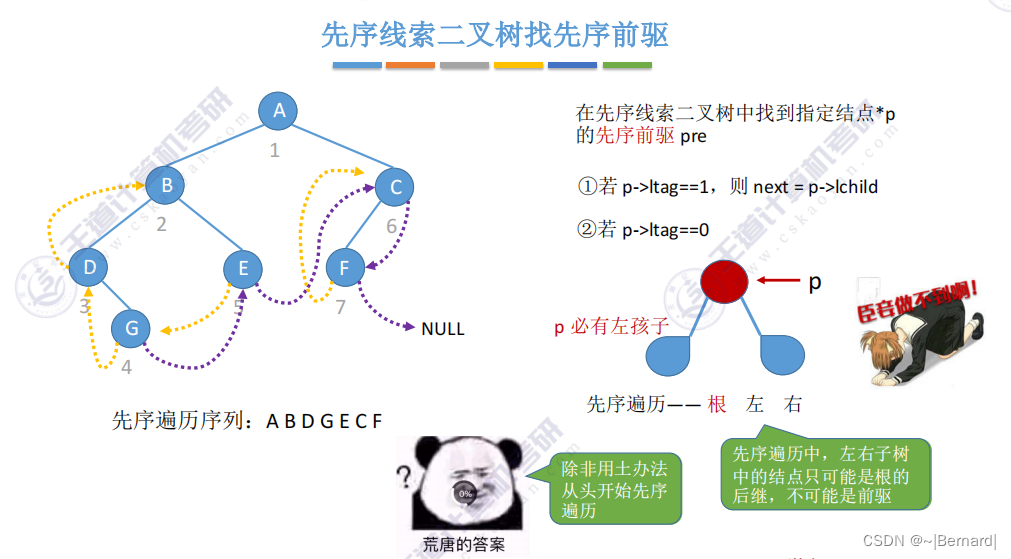
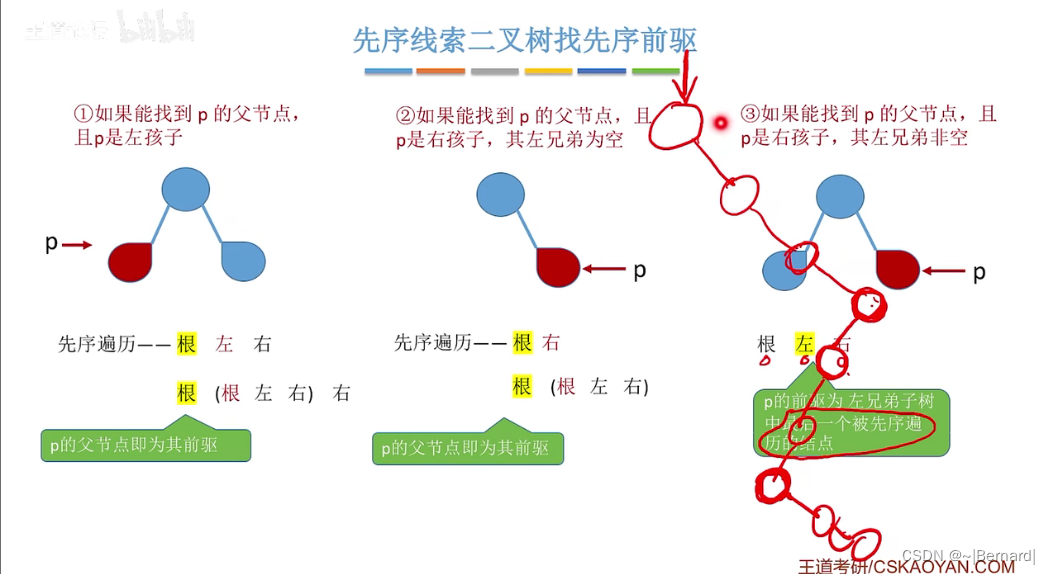
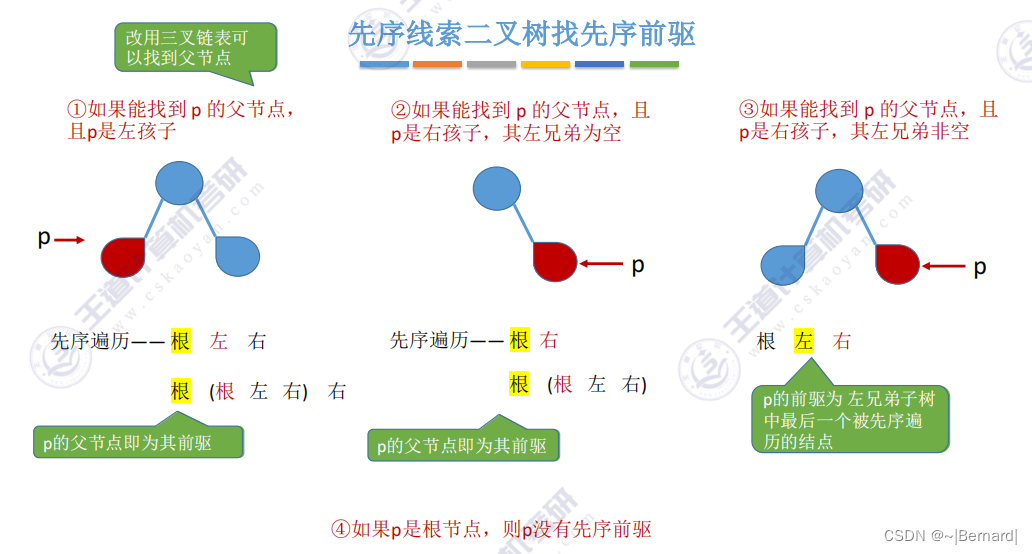
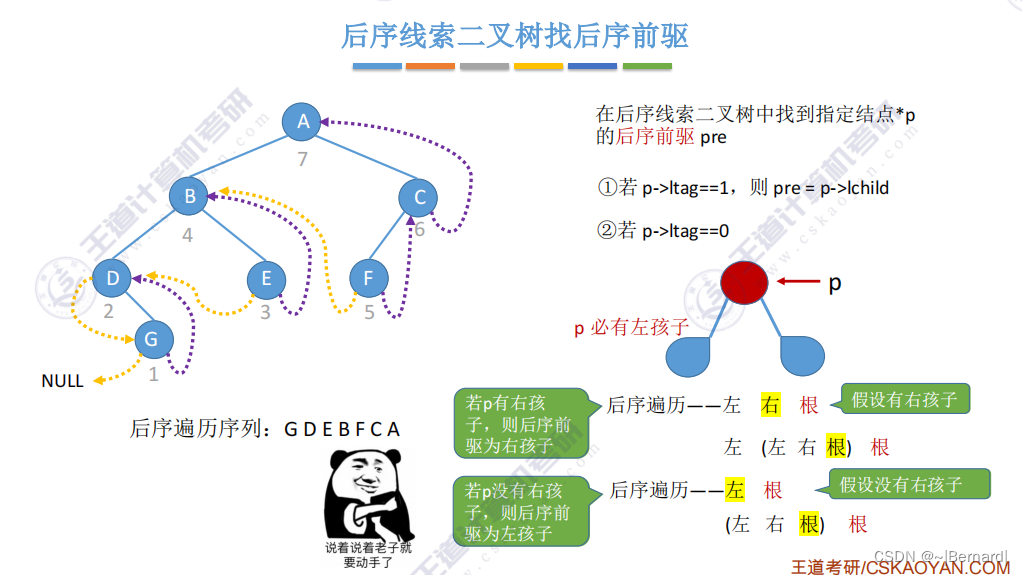
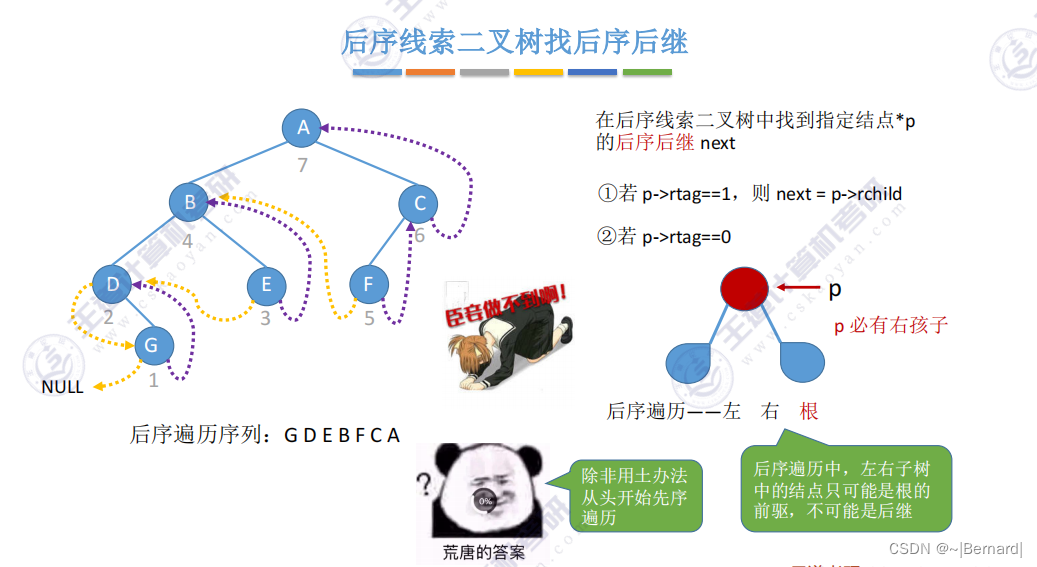
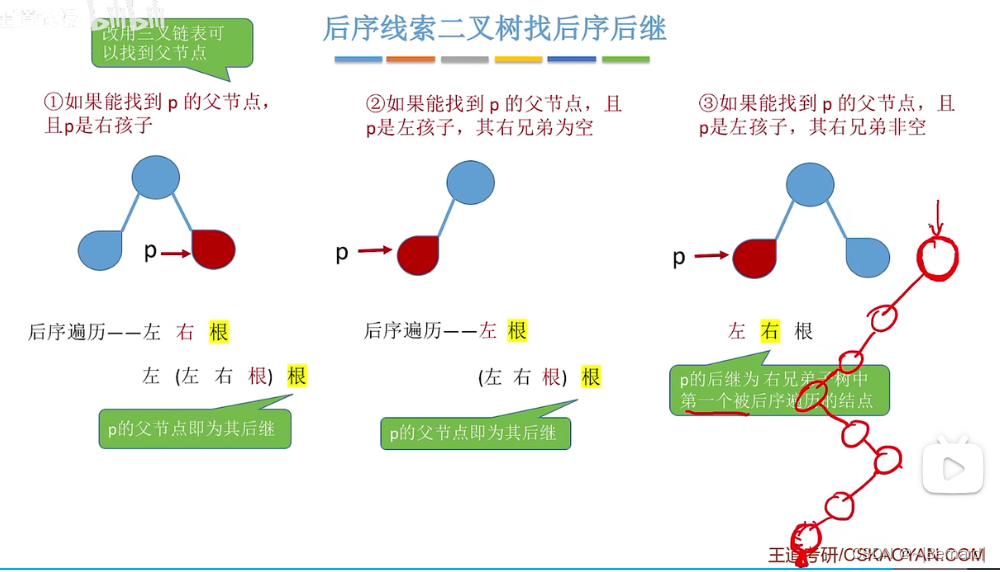
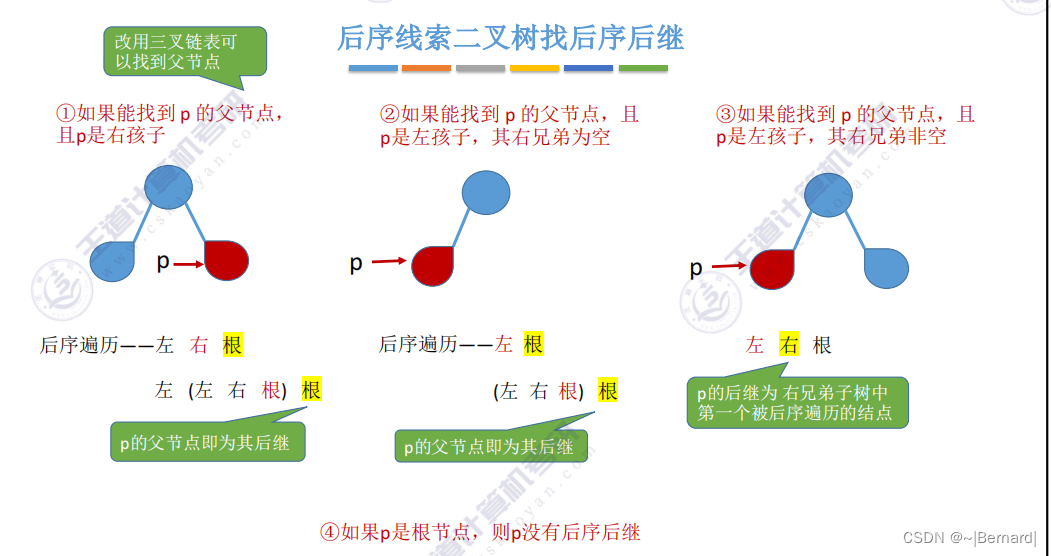
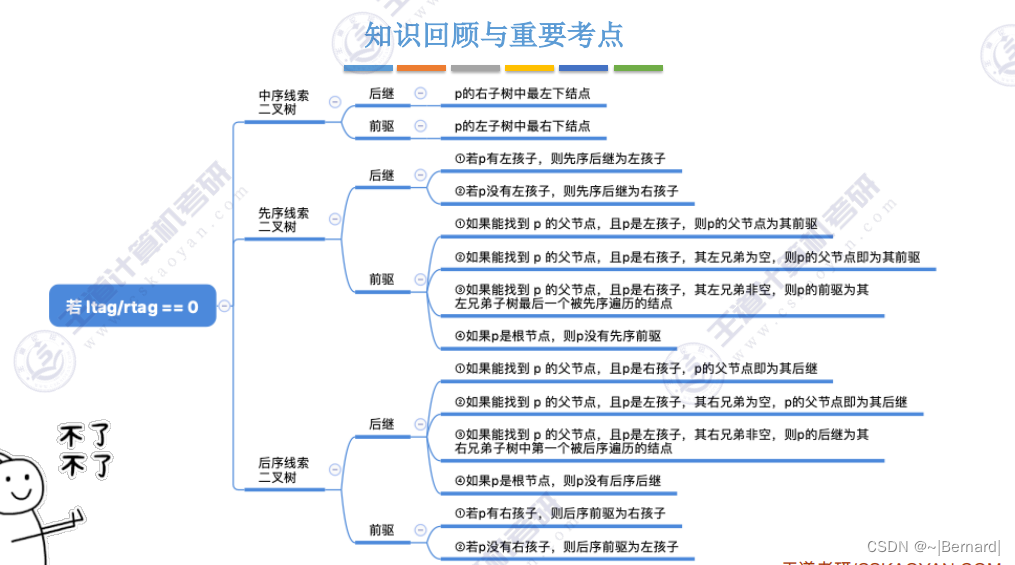
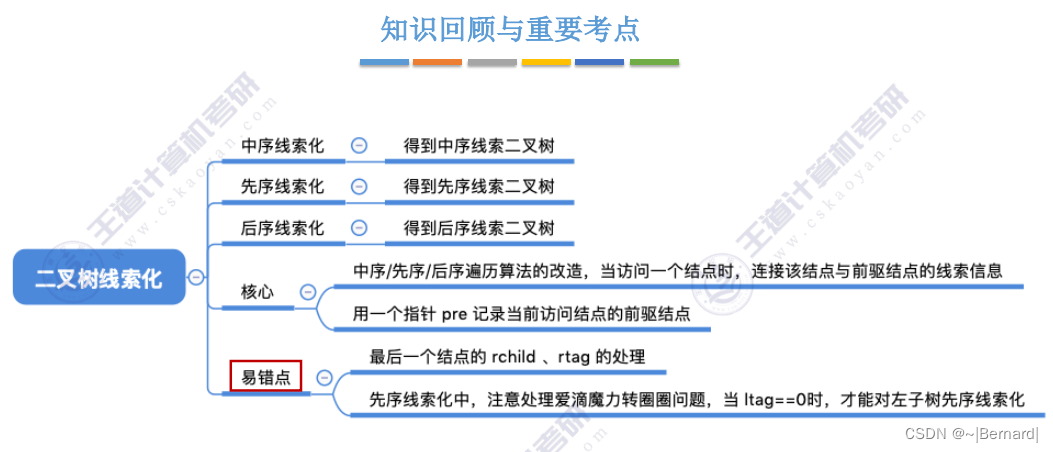 5.3.6 在线索二叉树中找前驱后继
5.3.6 在线索二叉树中找前驱后继
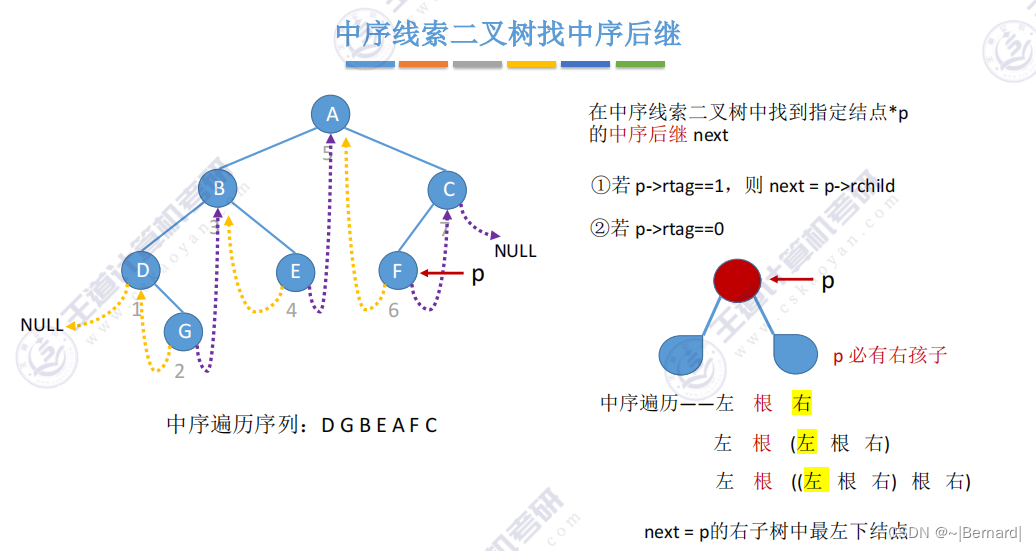
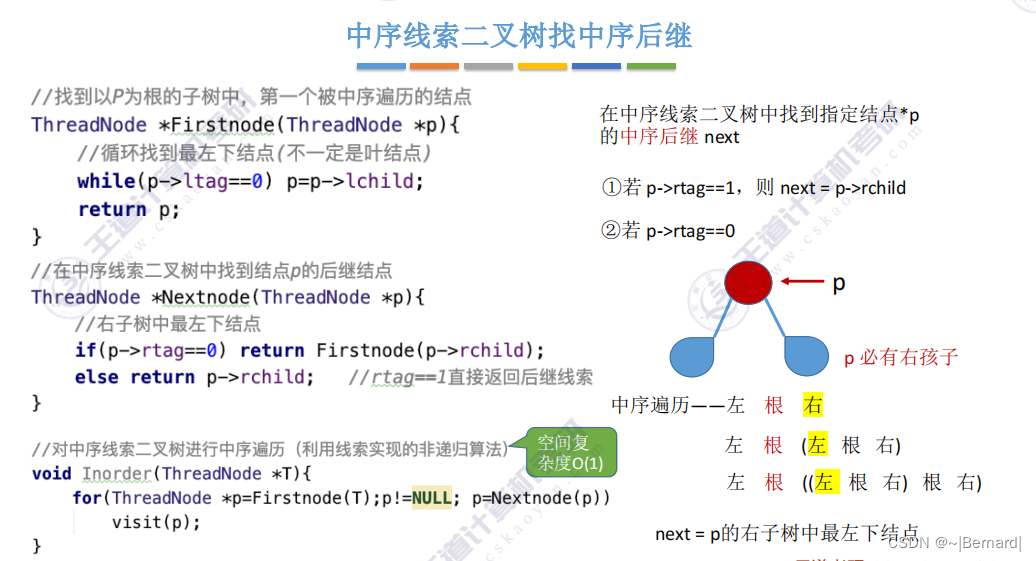
 5.4.1 树的存储结构
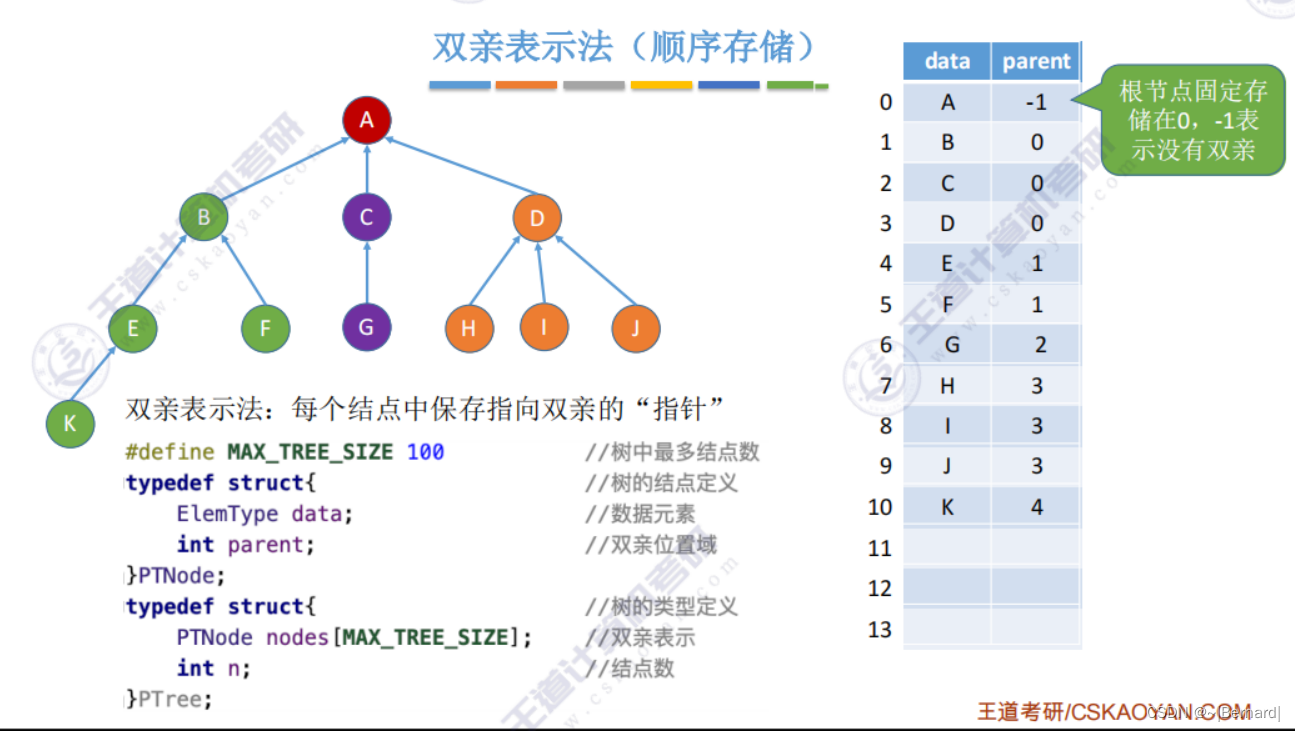
5.4.1 树的存储结构

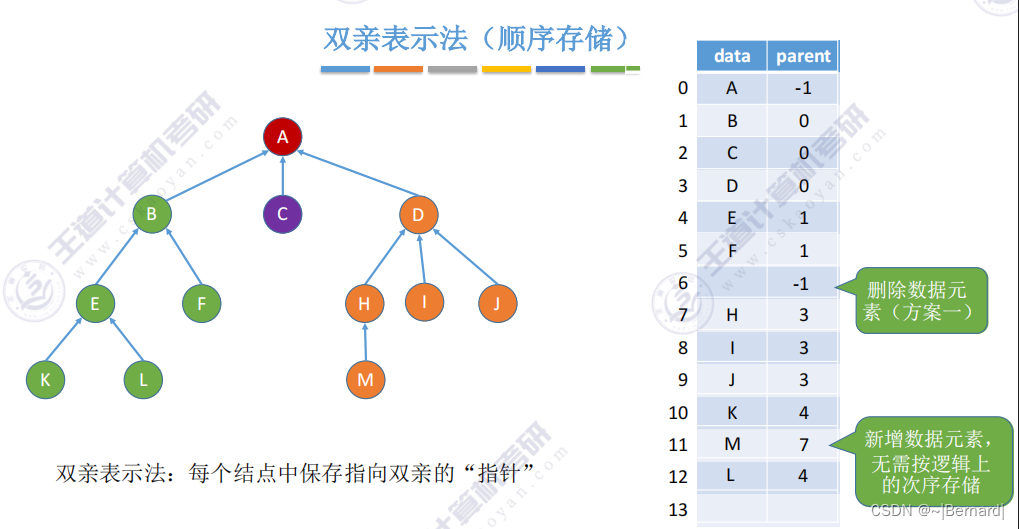
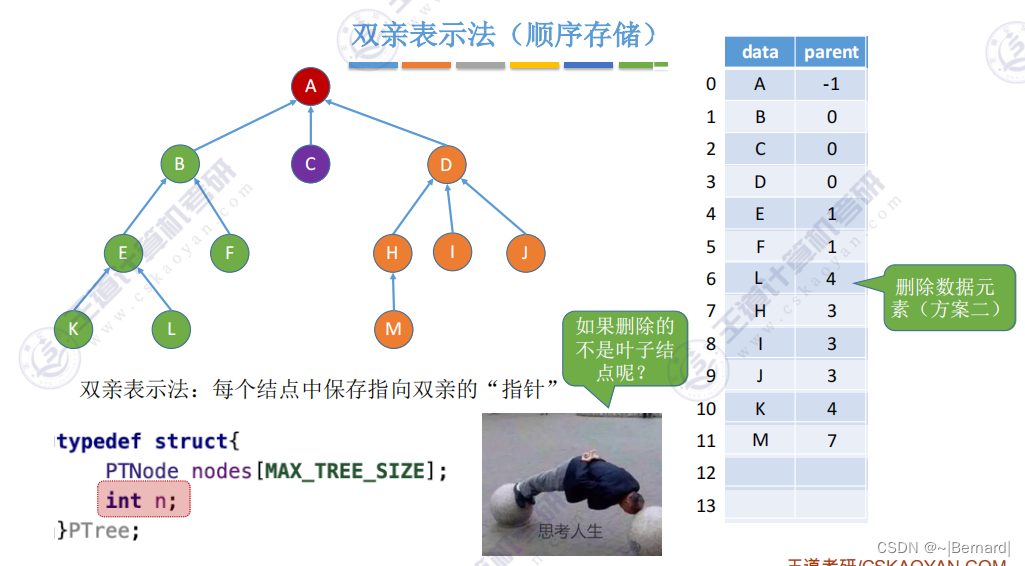


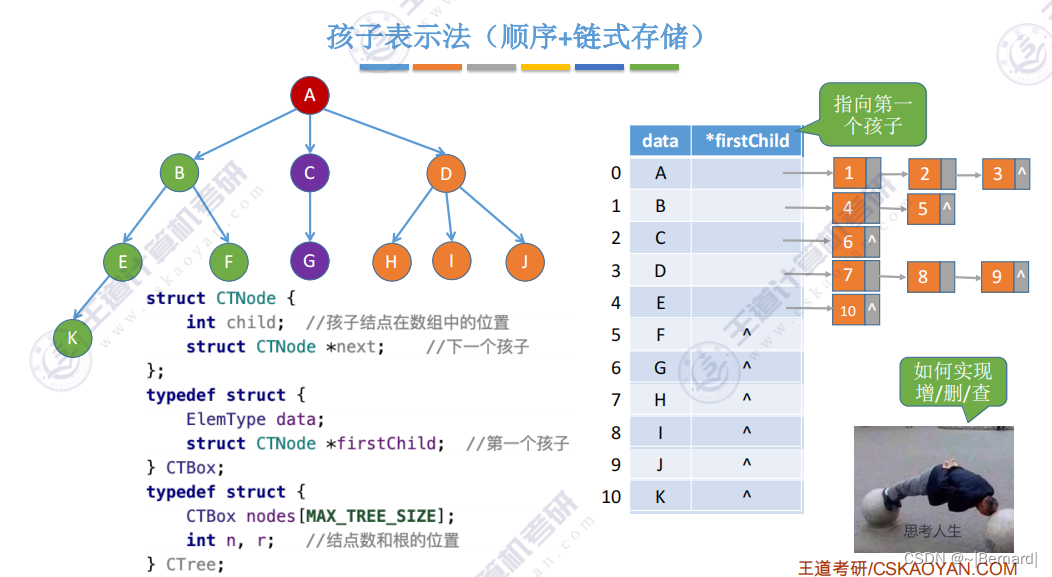
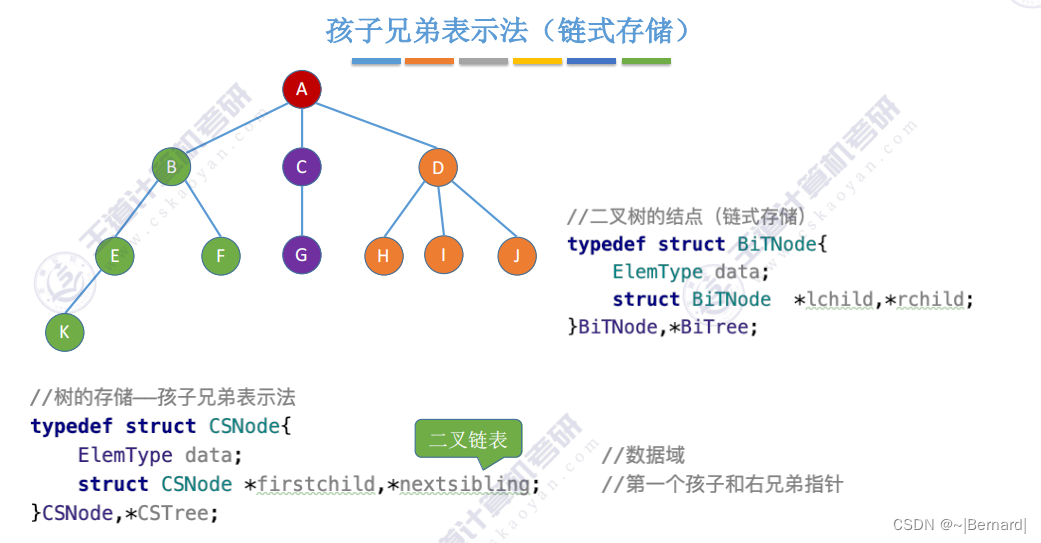
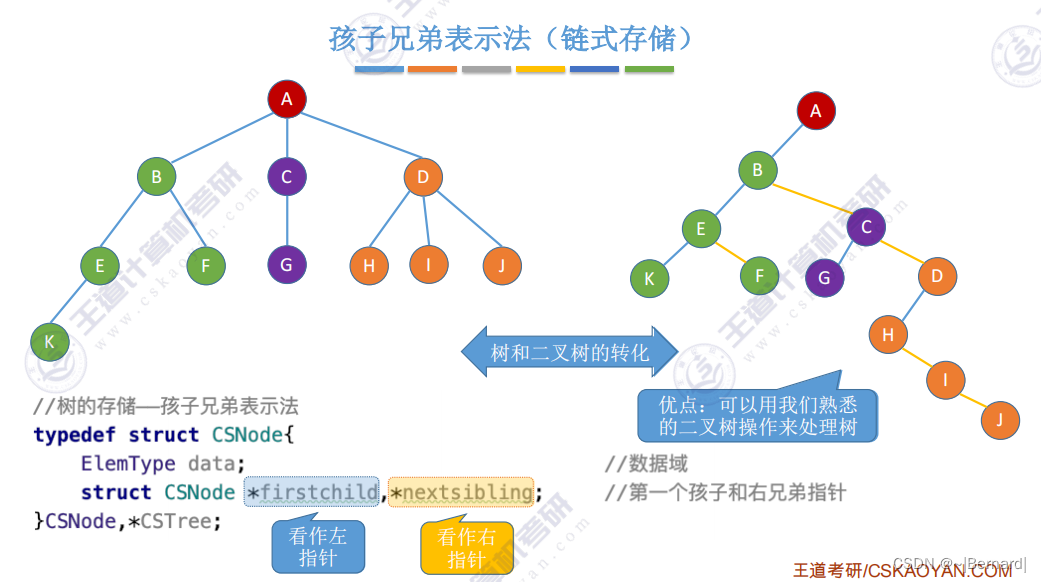
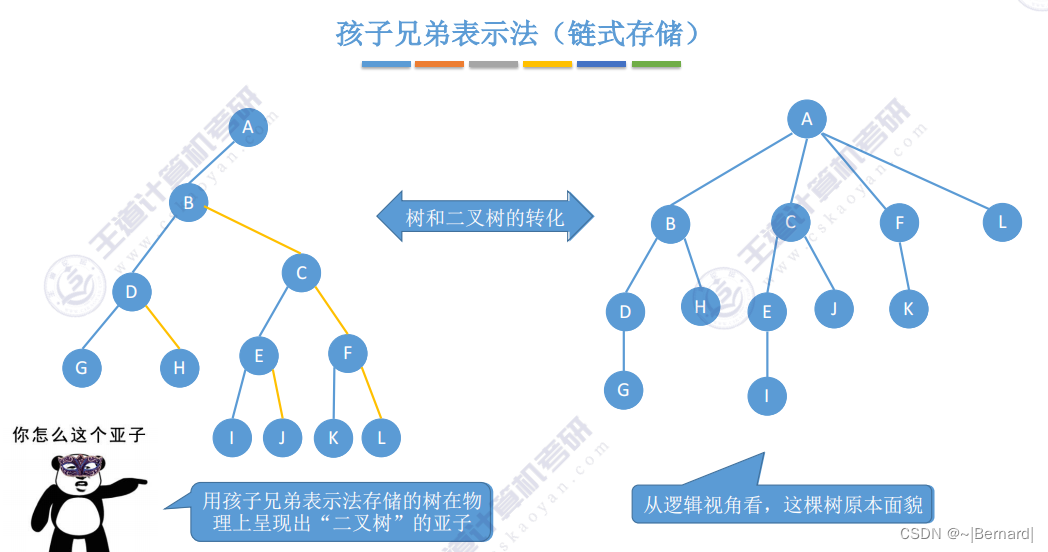
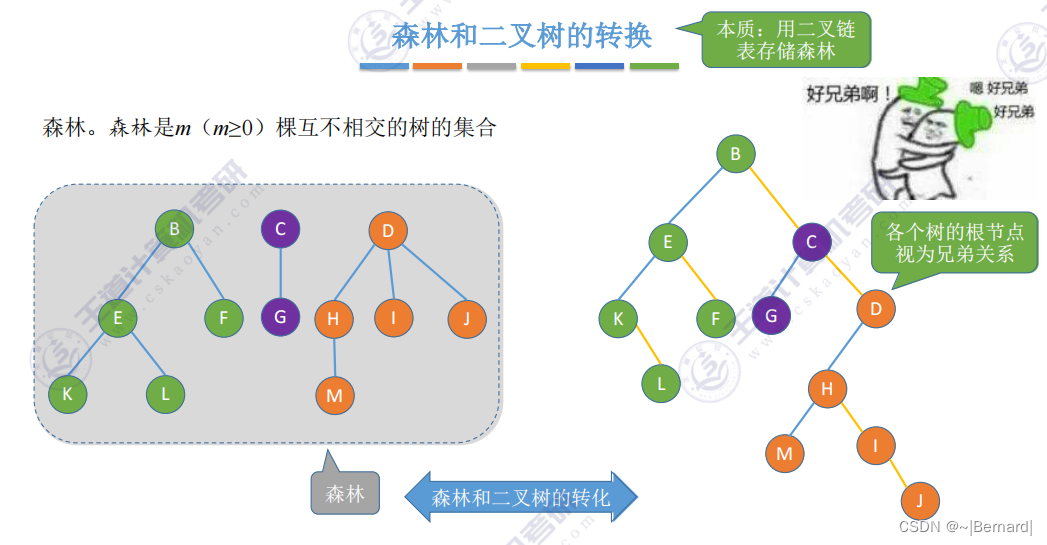
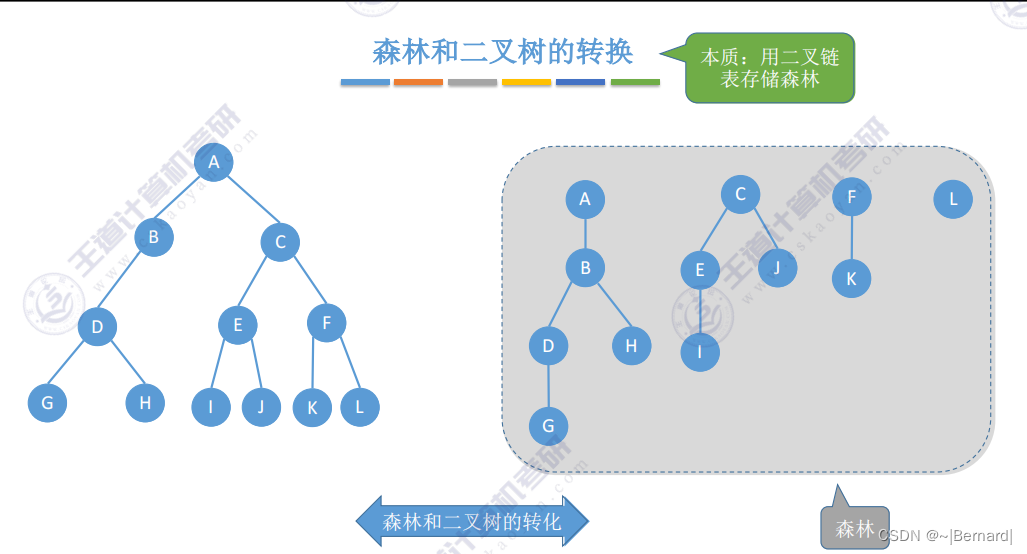
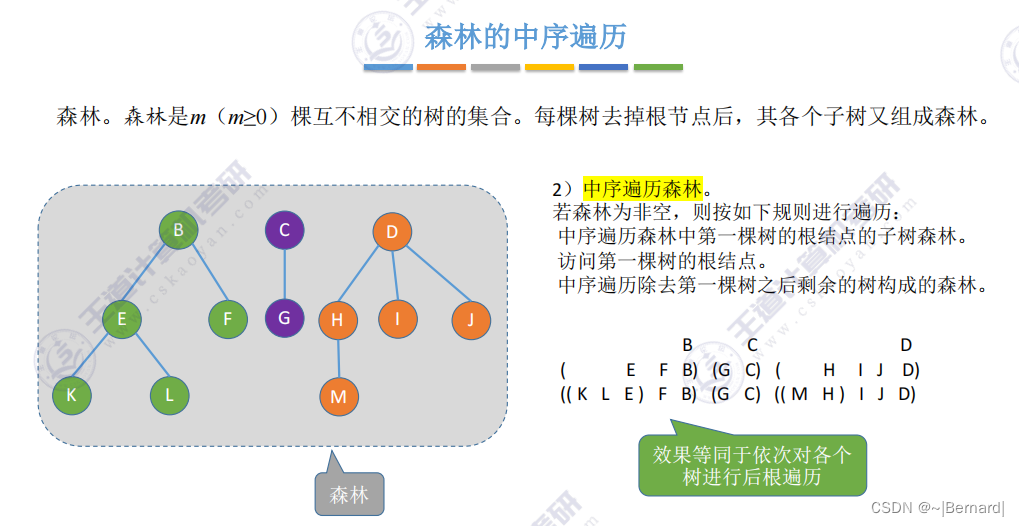
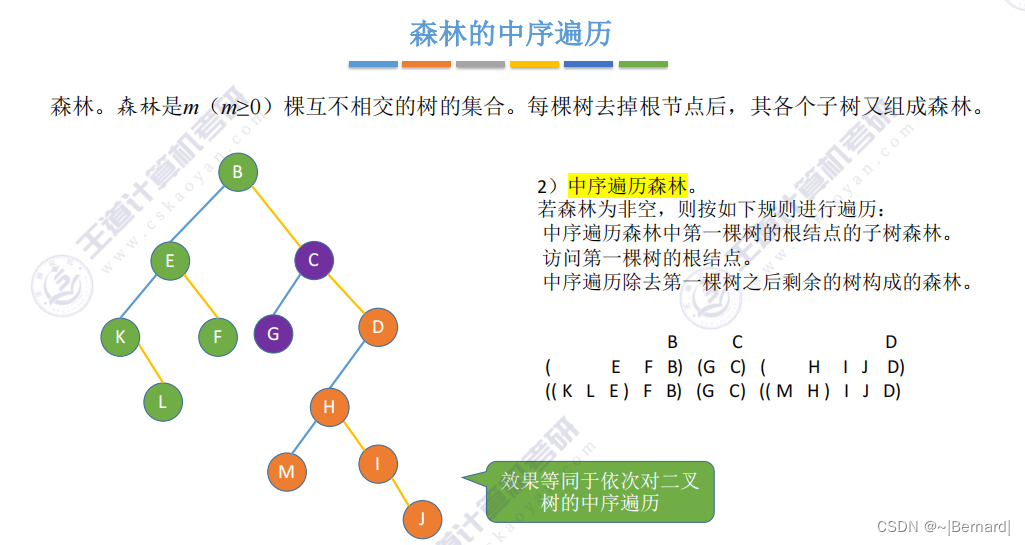
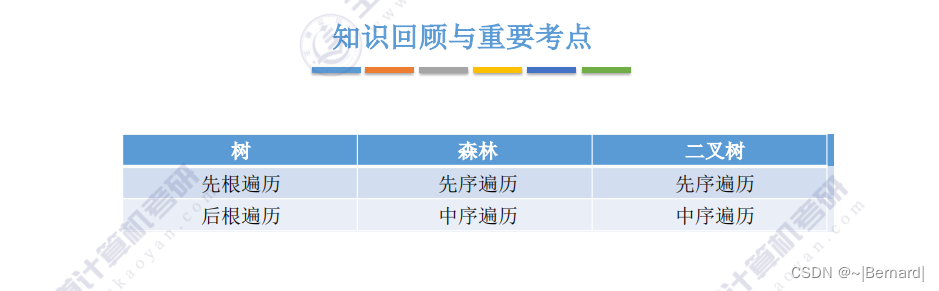
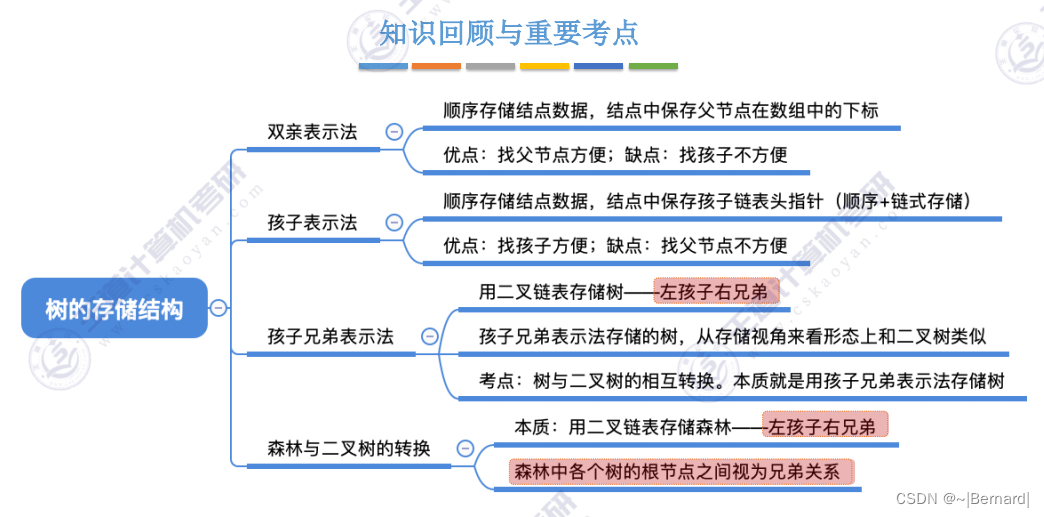 5.4.2 树和森林的遍历
5.4.2 树和森林的遍历

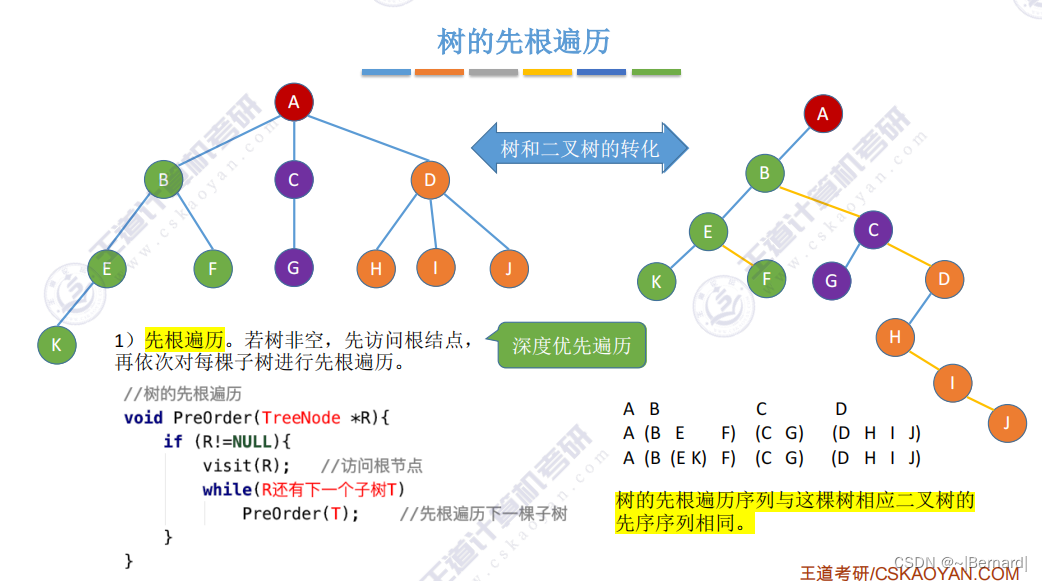



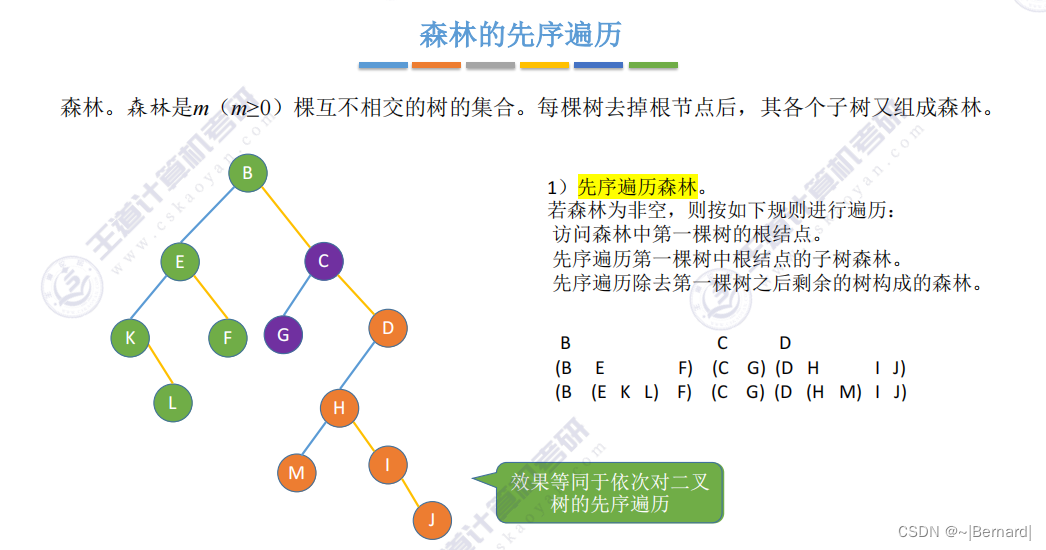
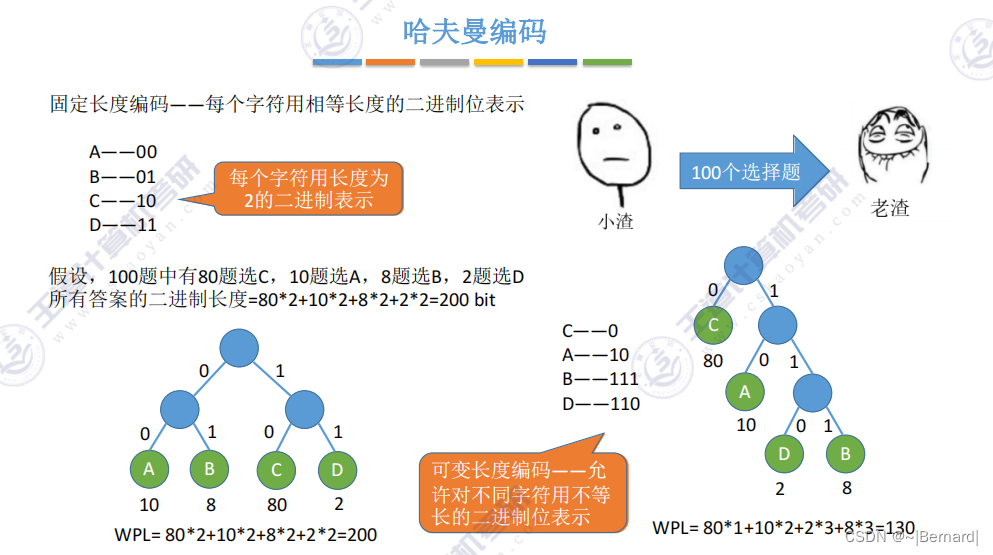
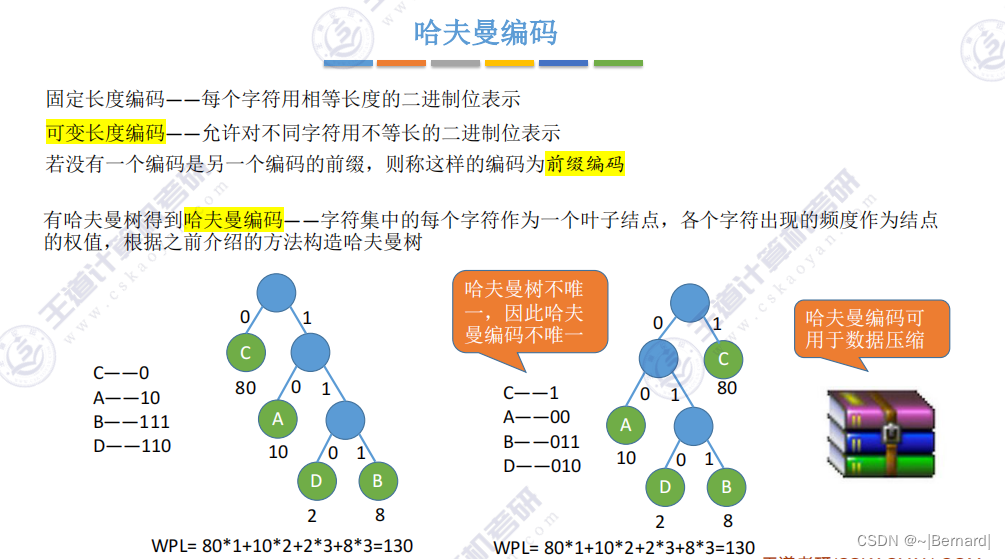
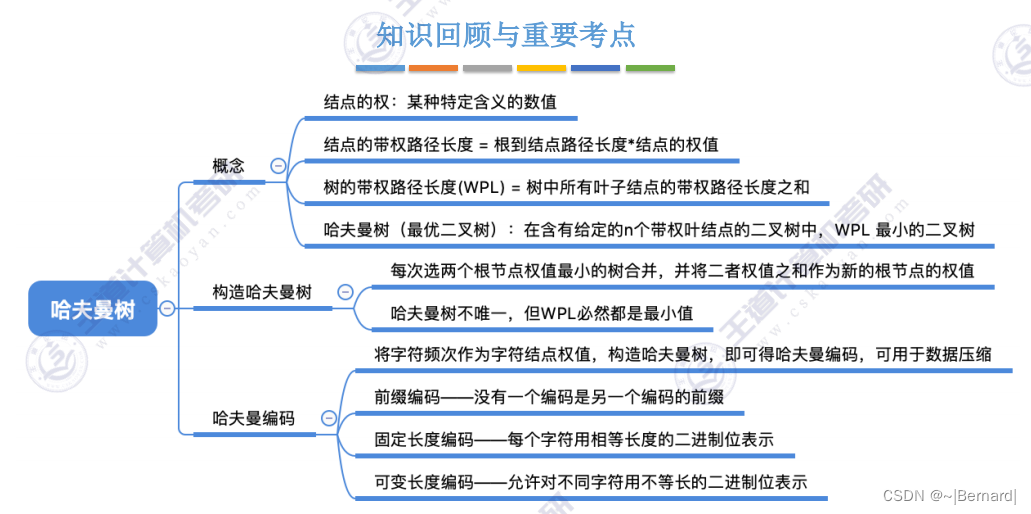
 5.5.1 哈夫曼树
5.5.1 哈夫曼树
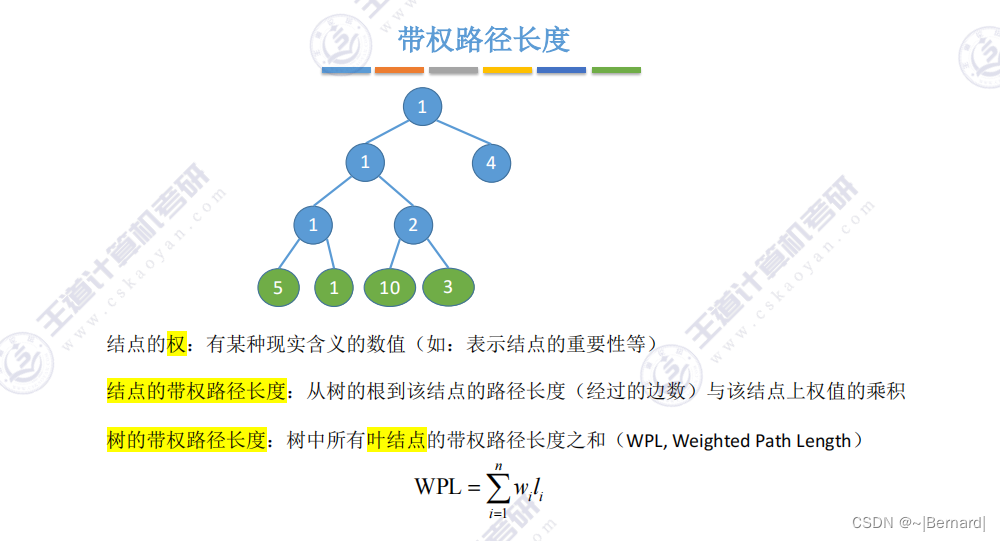
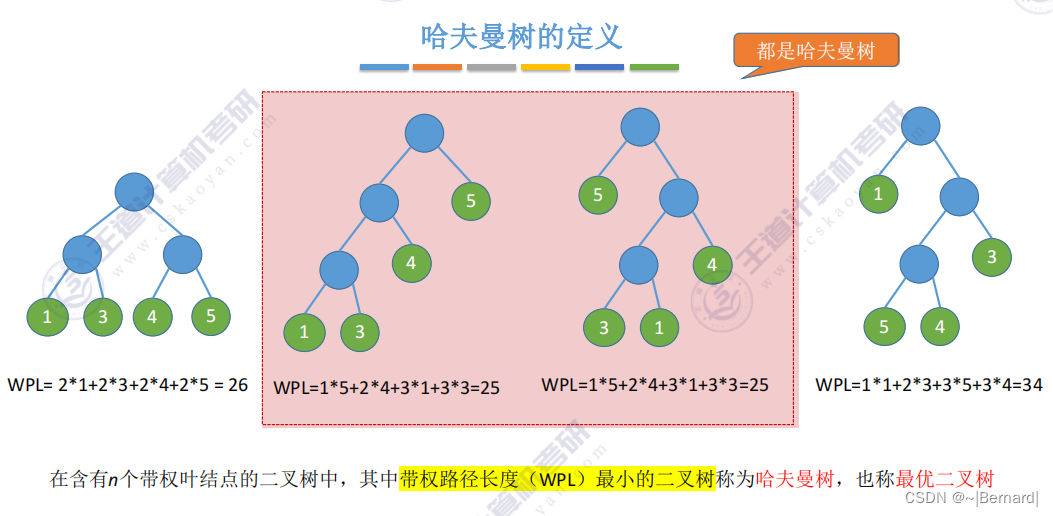
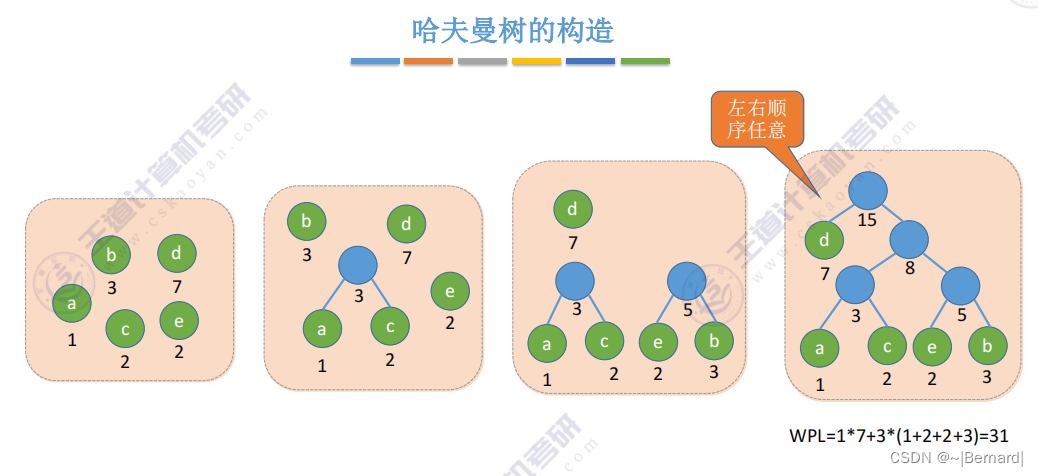
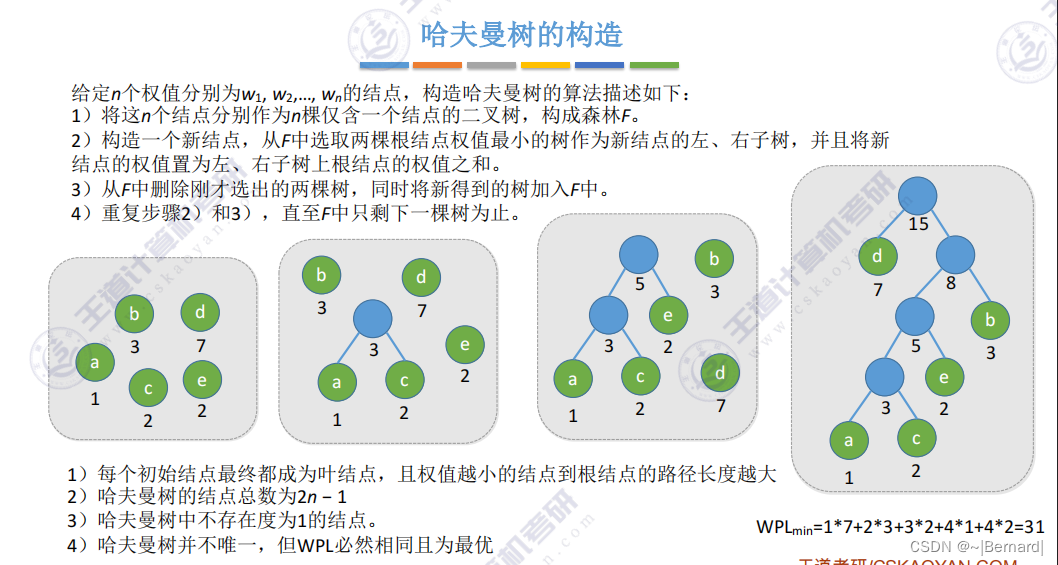 n个节点会合并n-1次,每一次合并都会导致增加一个分支节点,因此哈夫曼树的节点总数是2n-1
n个节点会合并n-1次,每一次合并都会导致增加一个分支节点,因此哈夫曼树的节点总数是2n-1
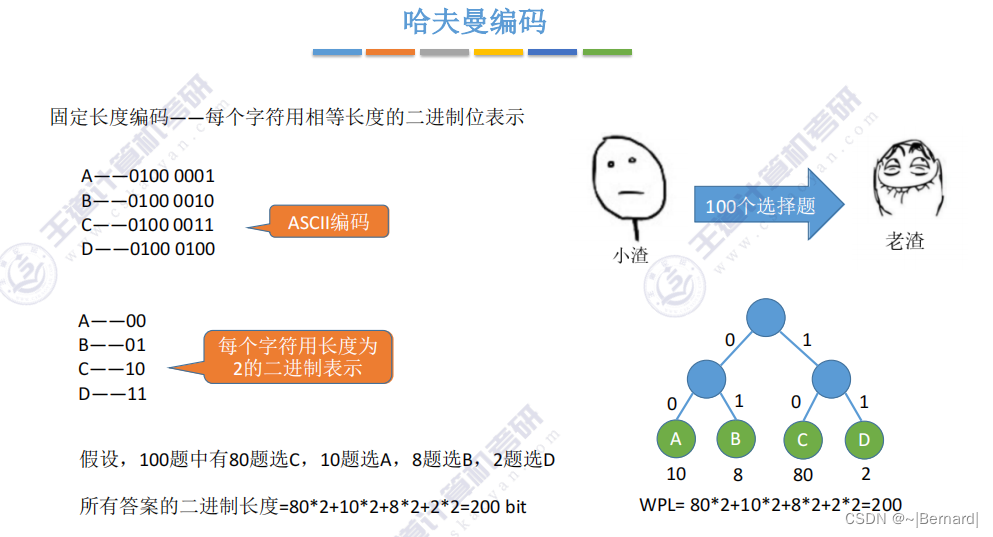


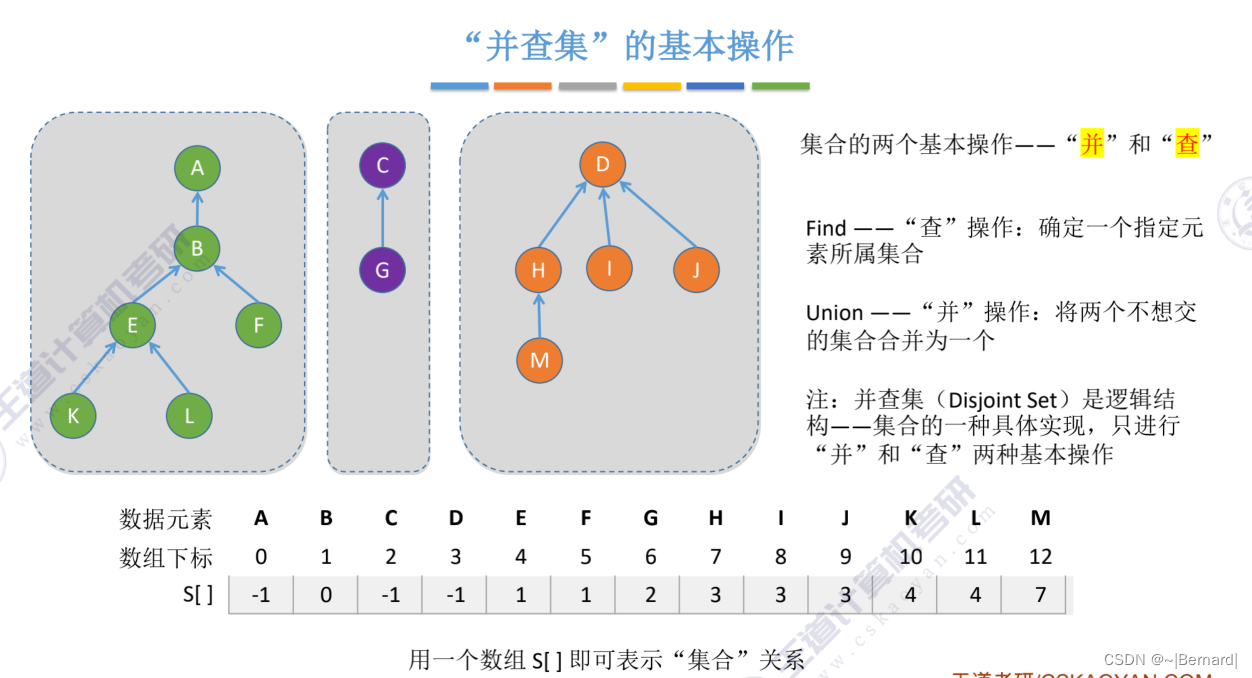
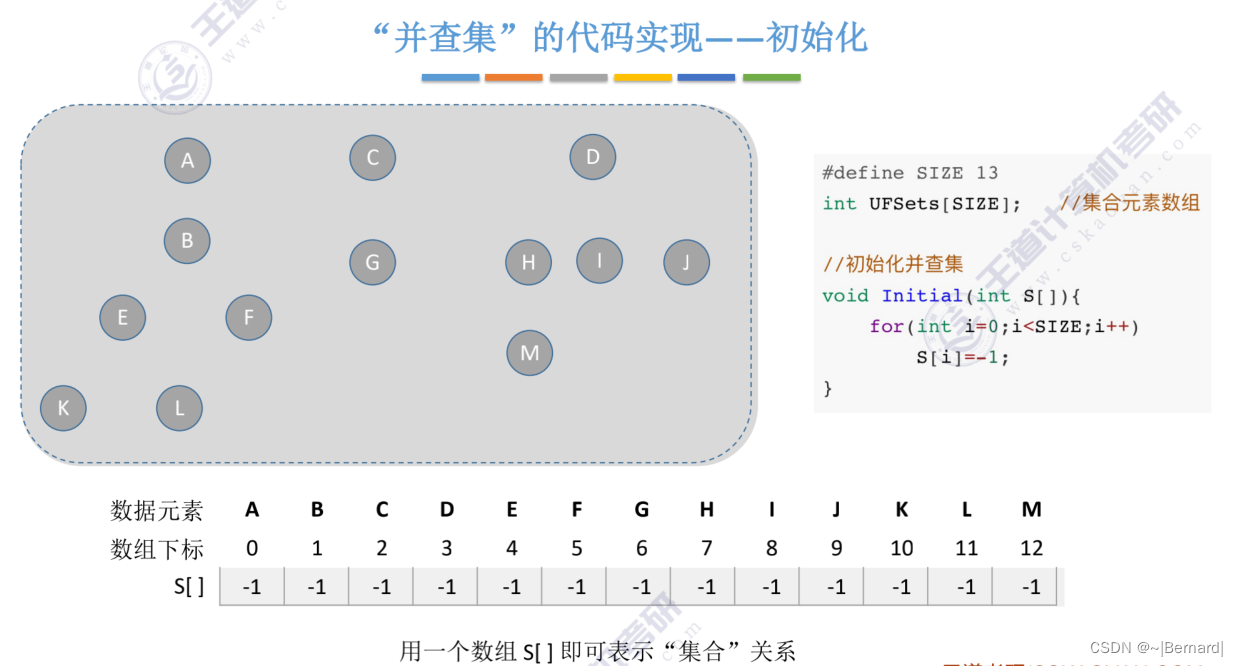
5.5.2 并查集
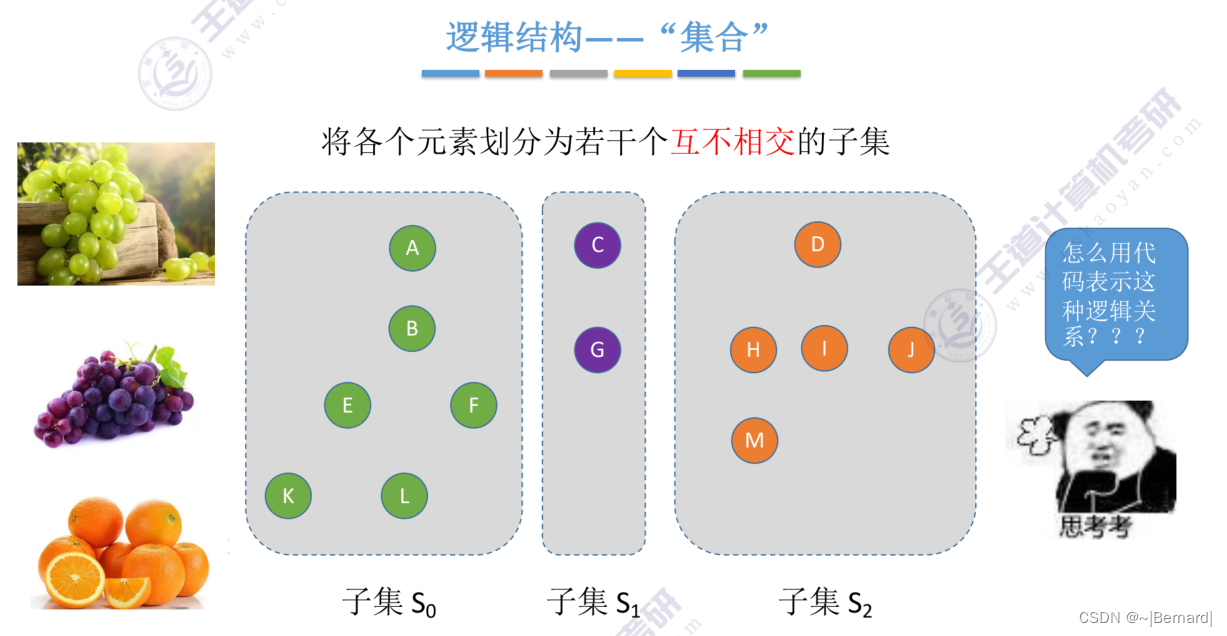

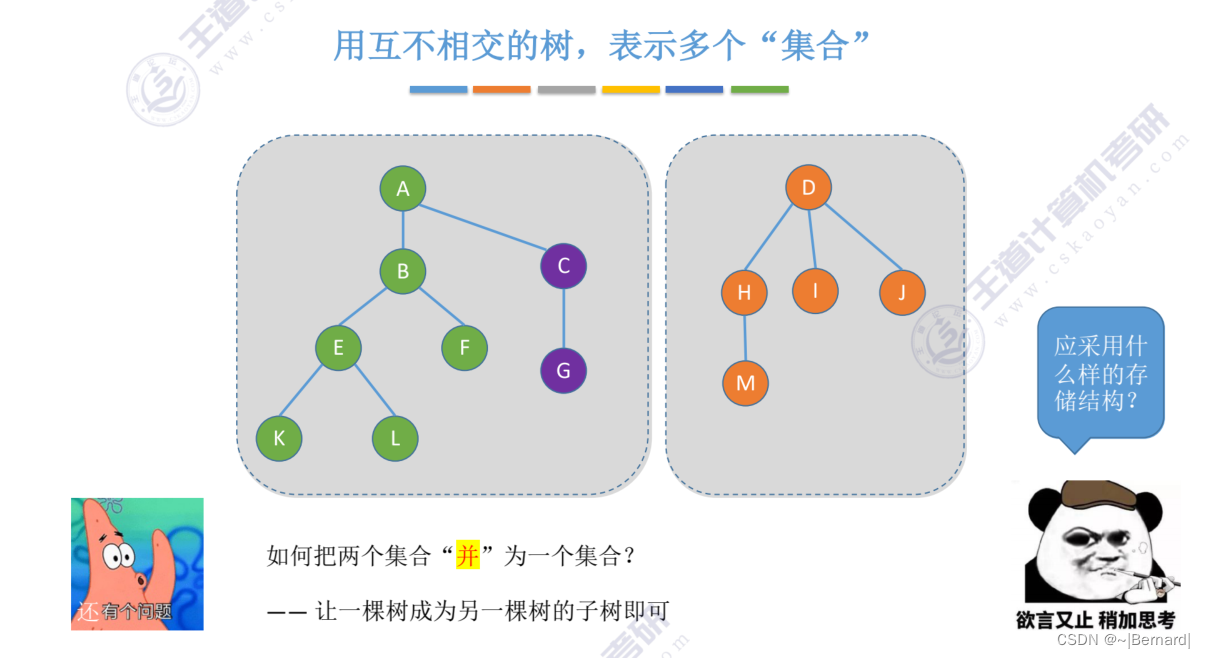
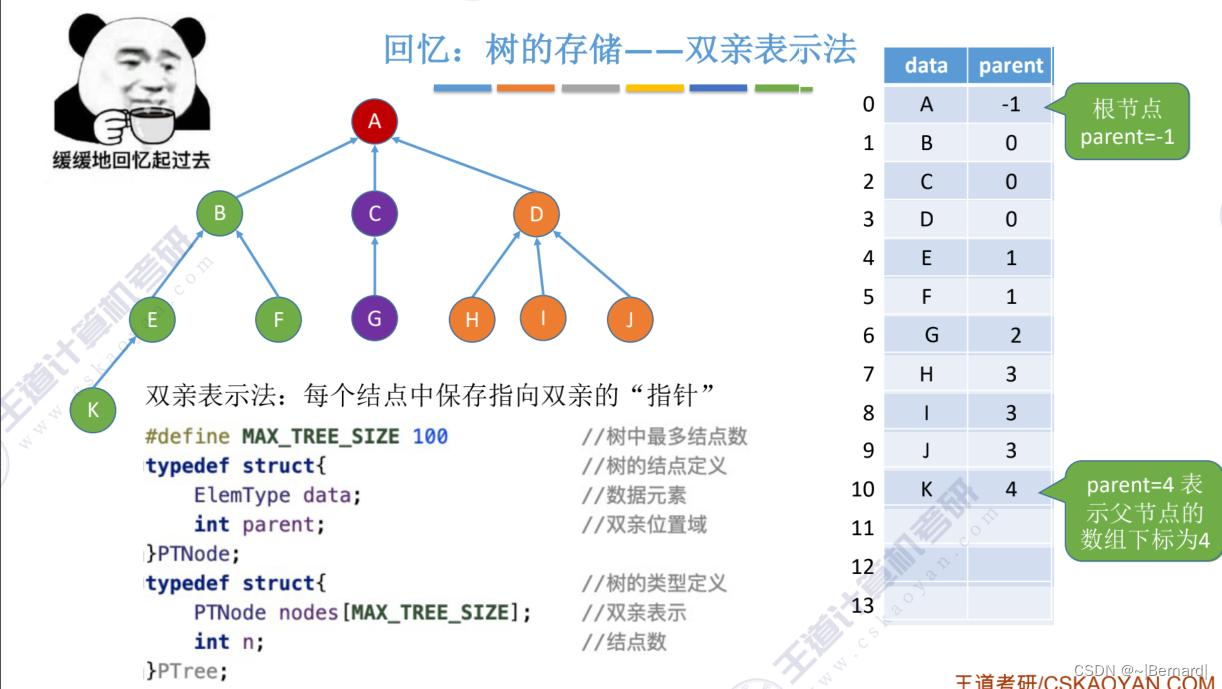
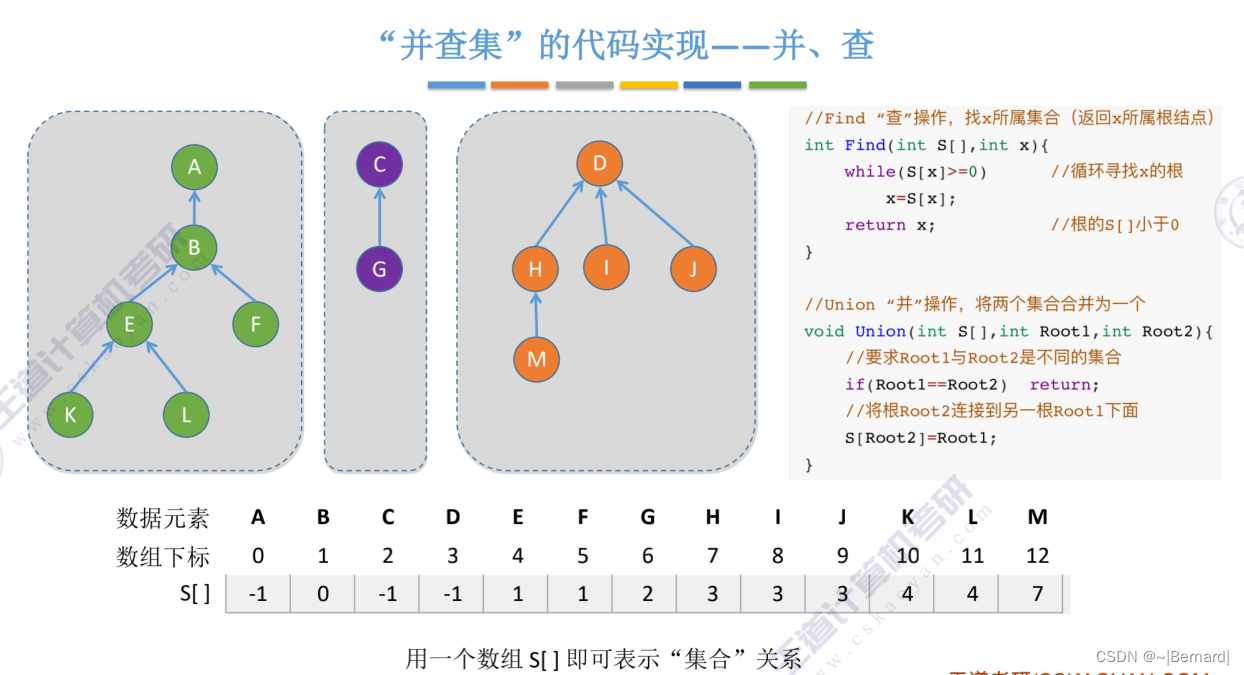
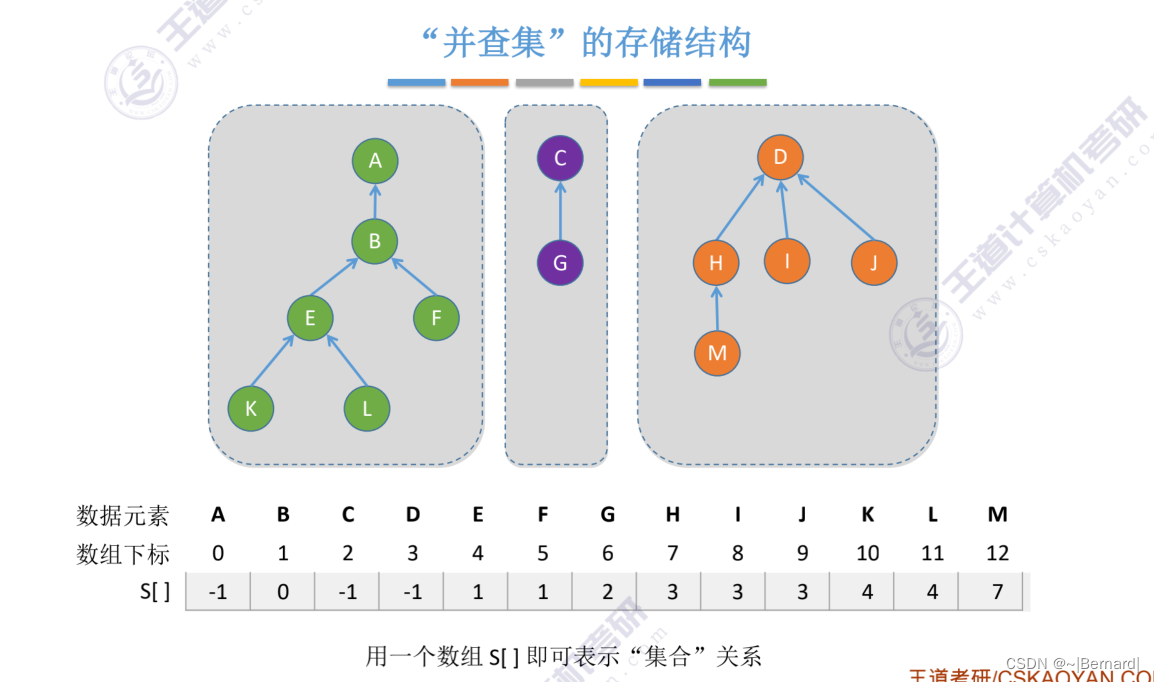 采用双亲表示法并和查的操作都是非常方便的
采用双亲表示法并和查的操作都是非常方便的
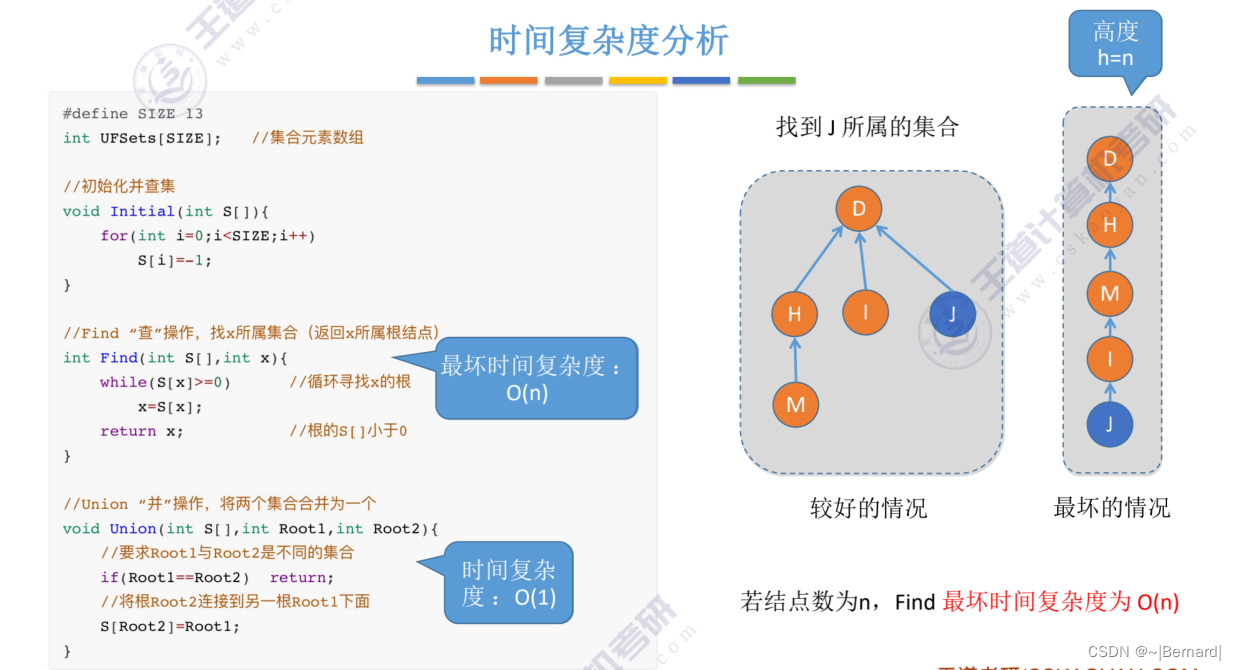

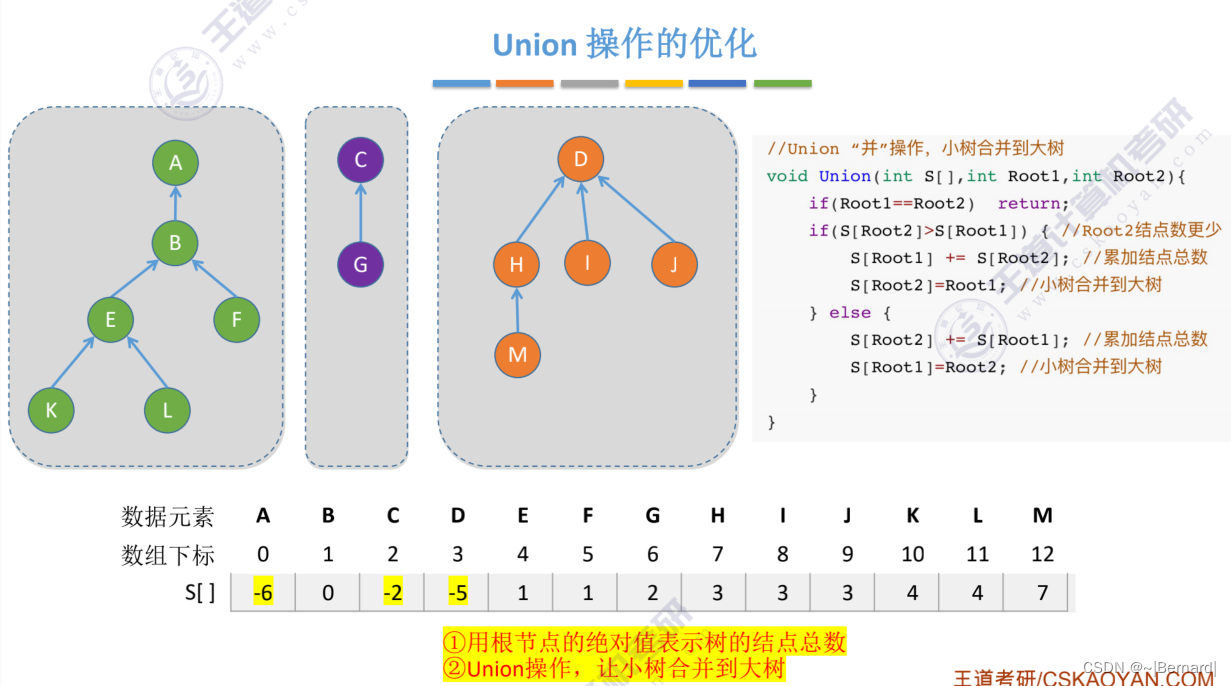

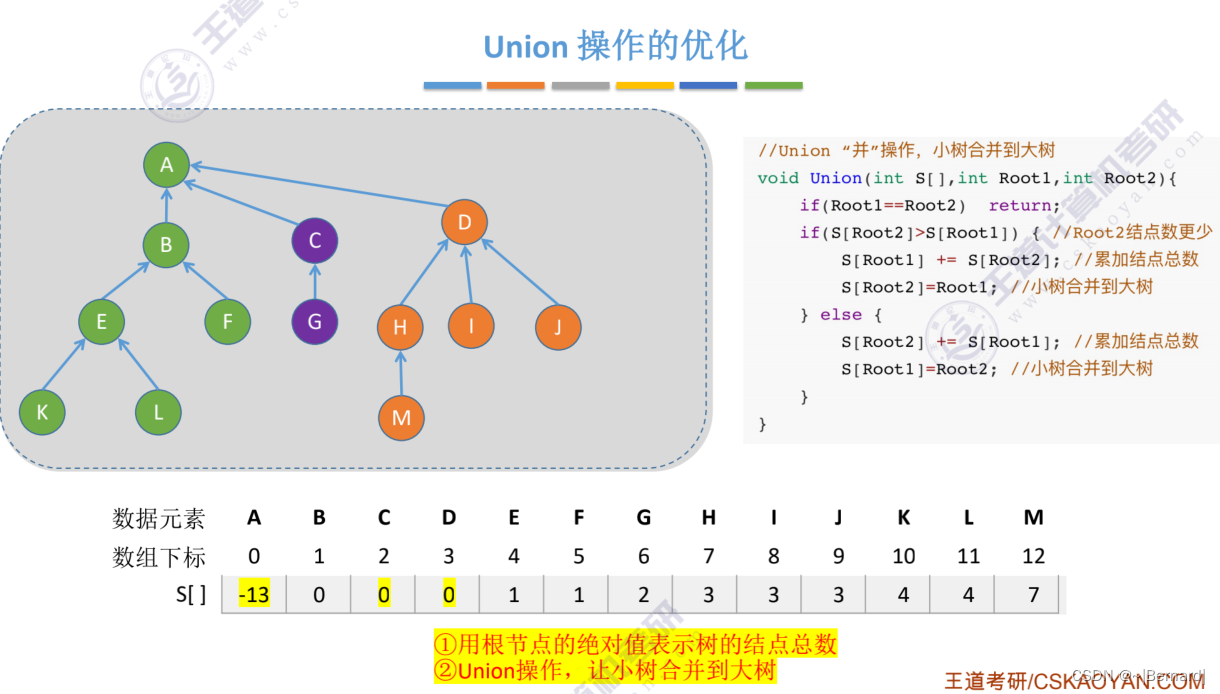
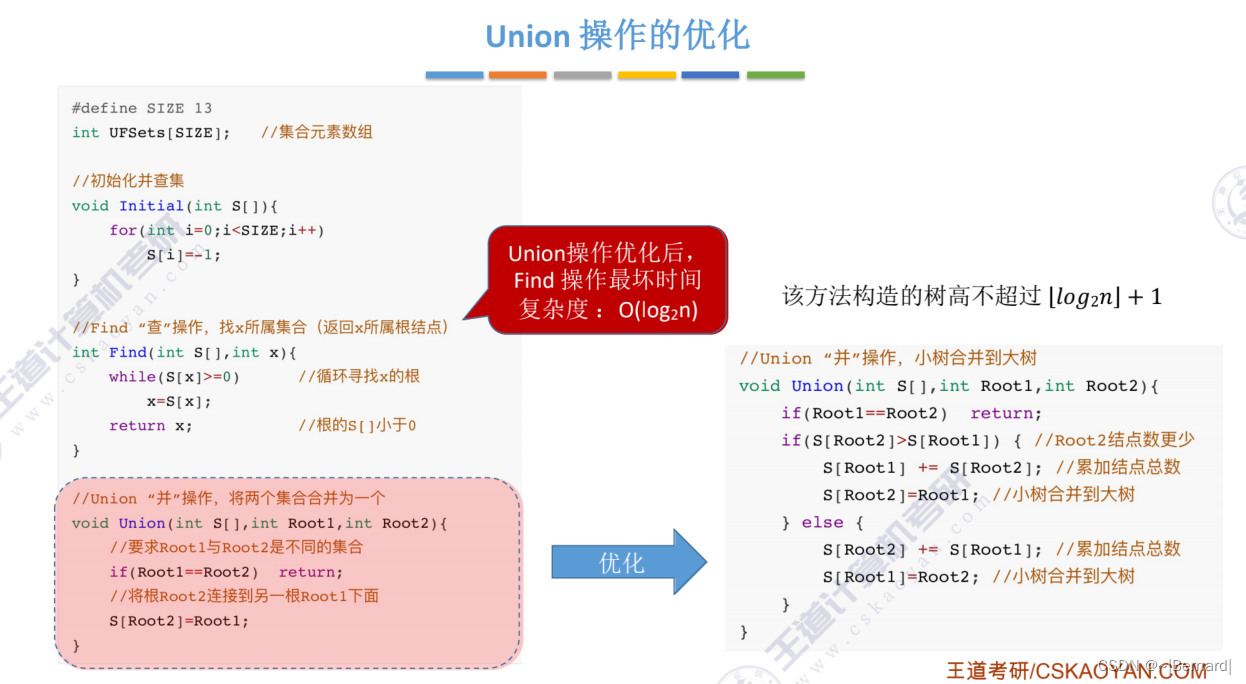
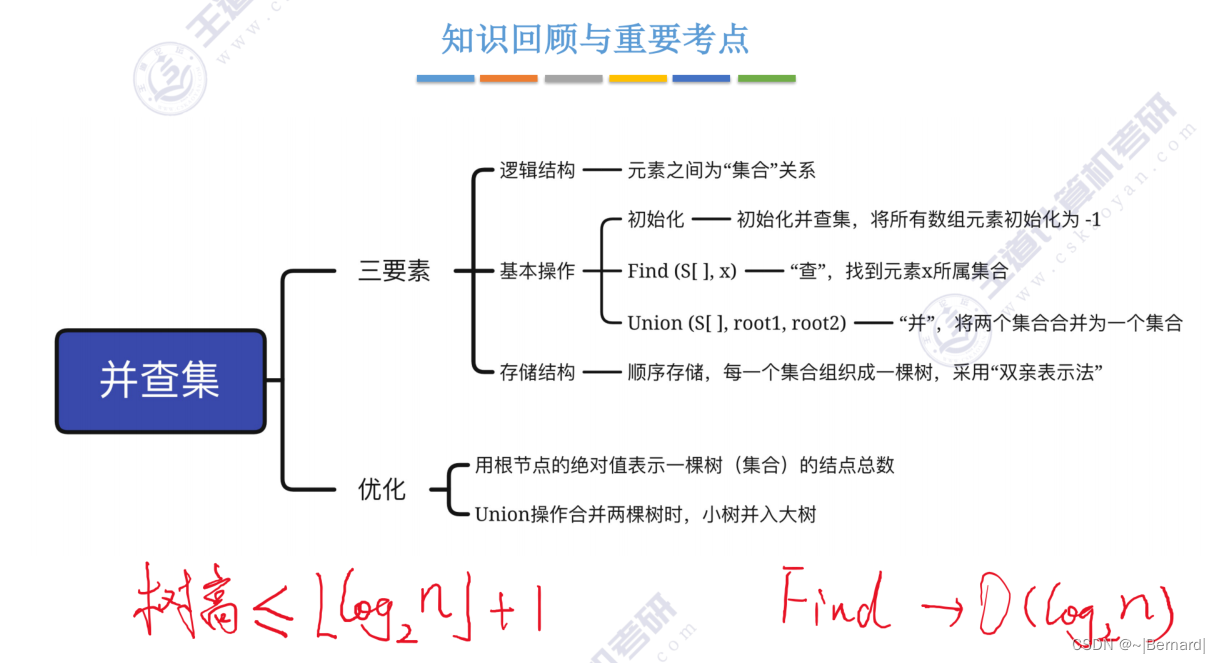
5.5.3 并查集的进一步优化

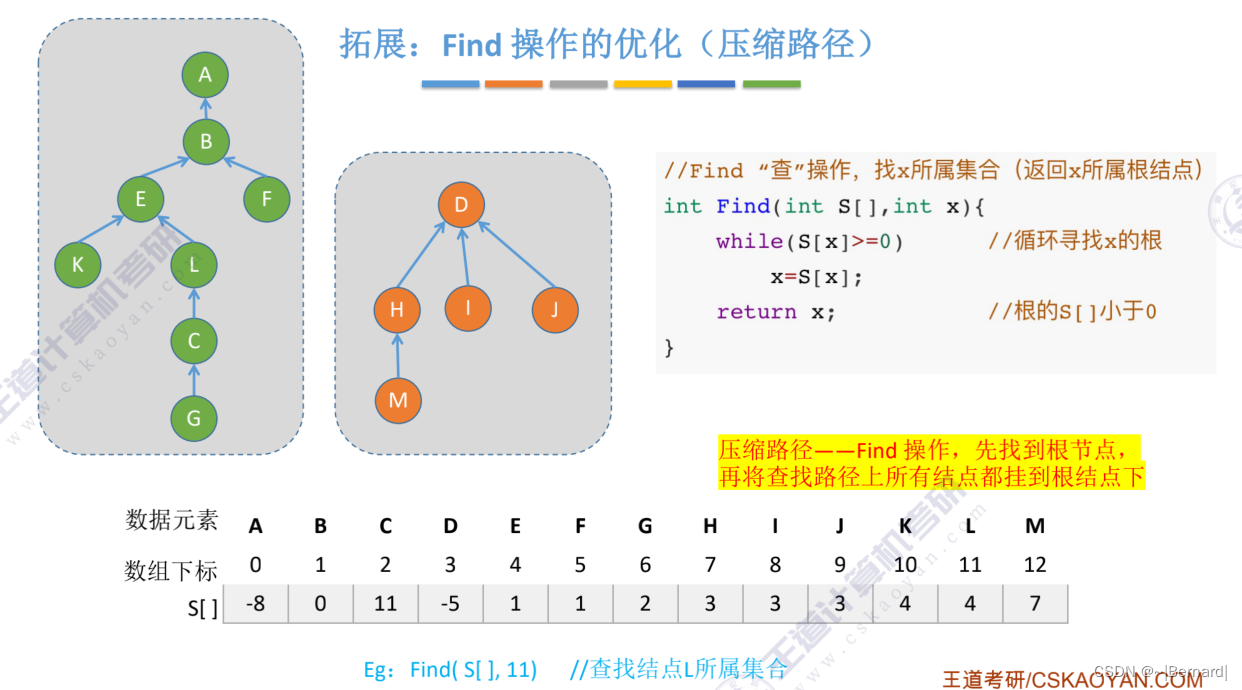

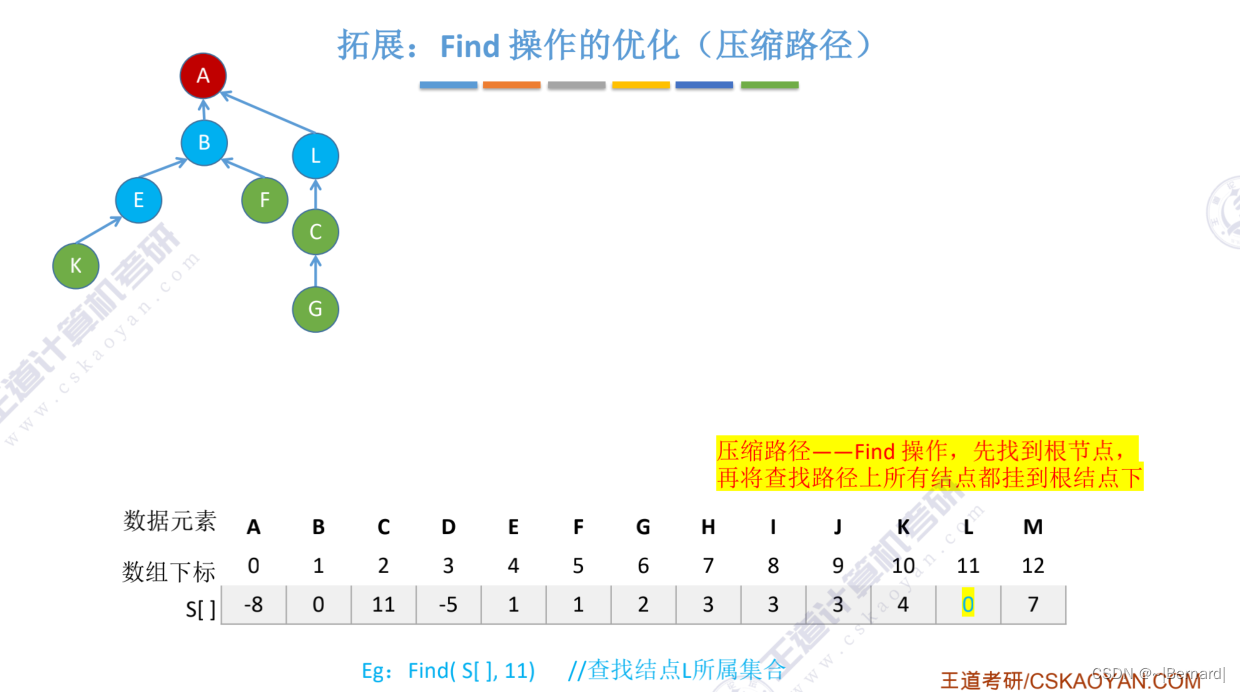
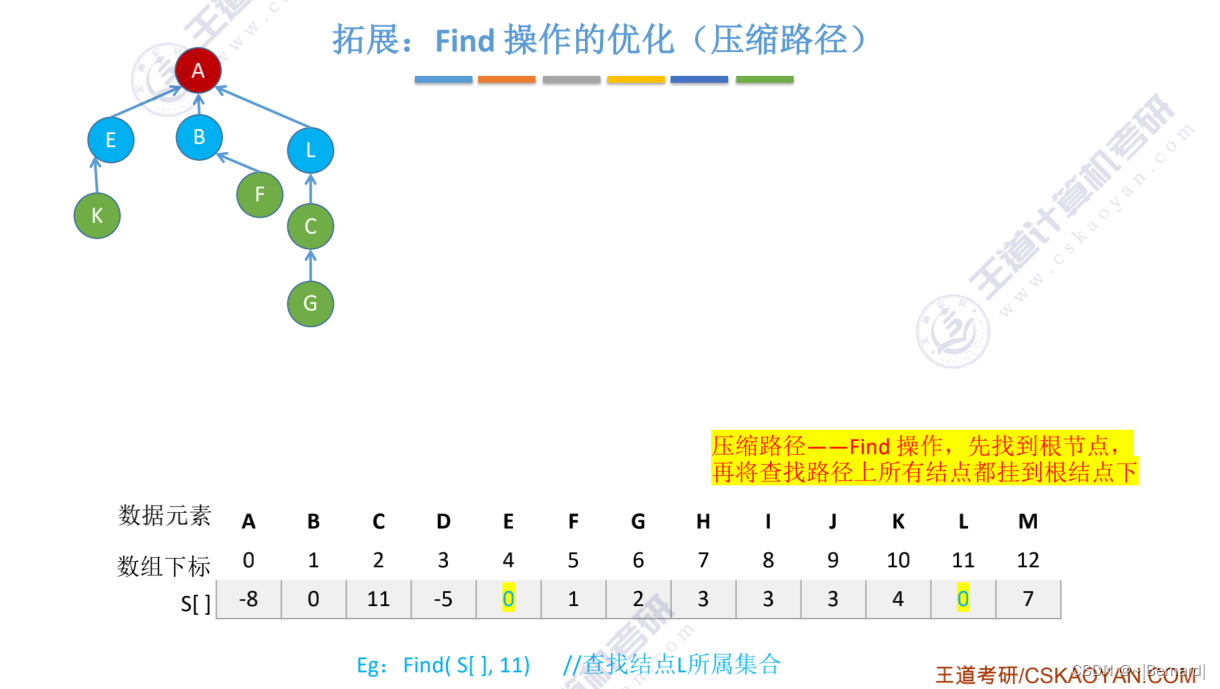
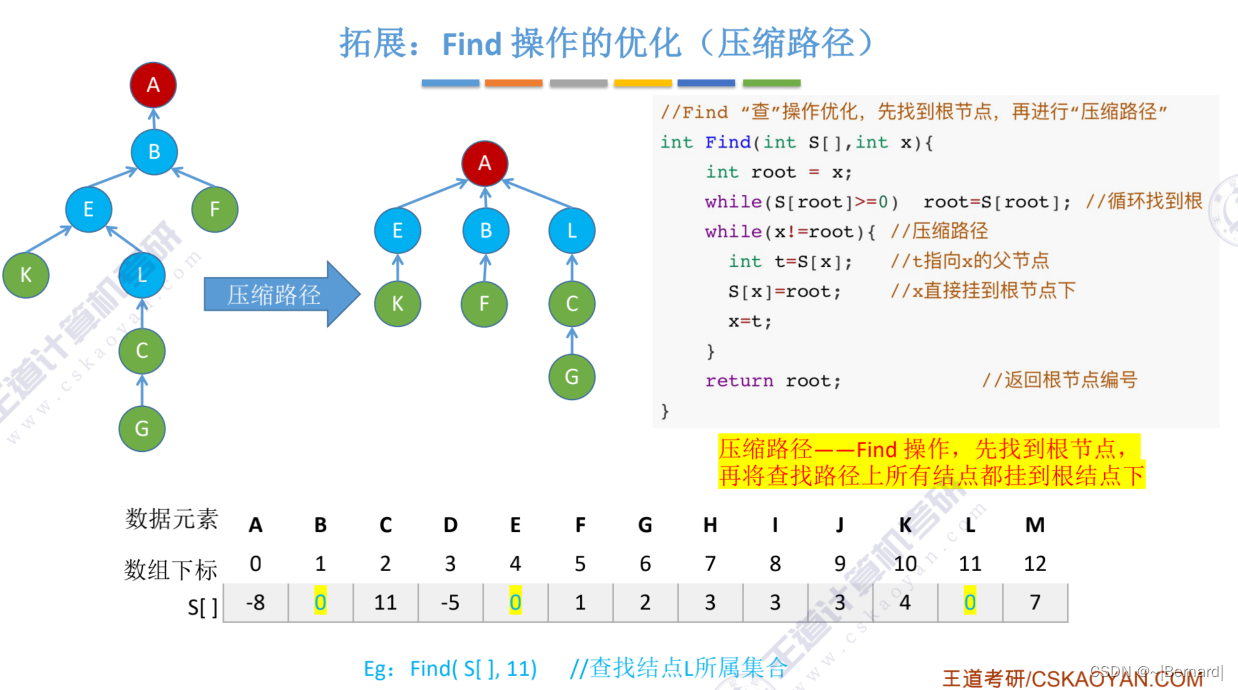

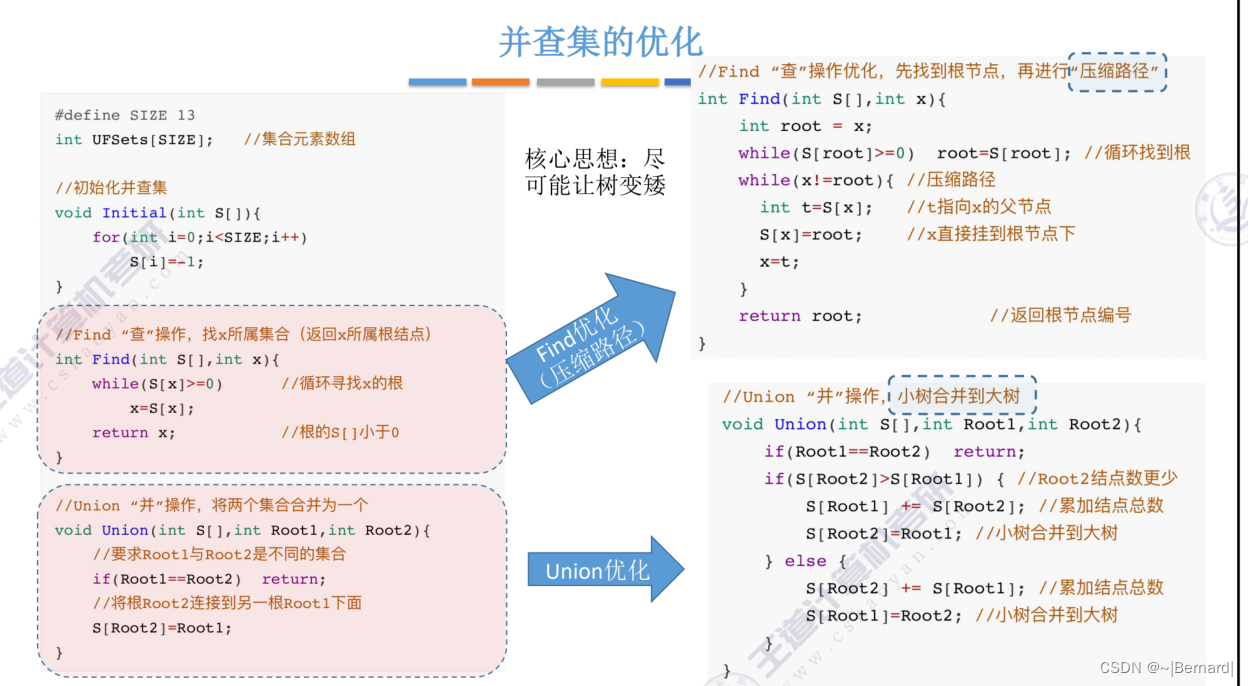
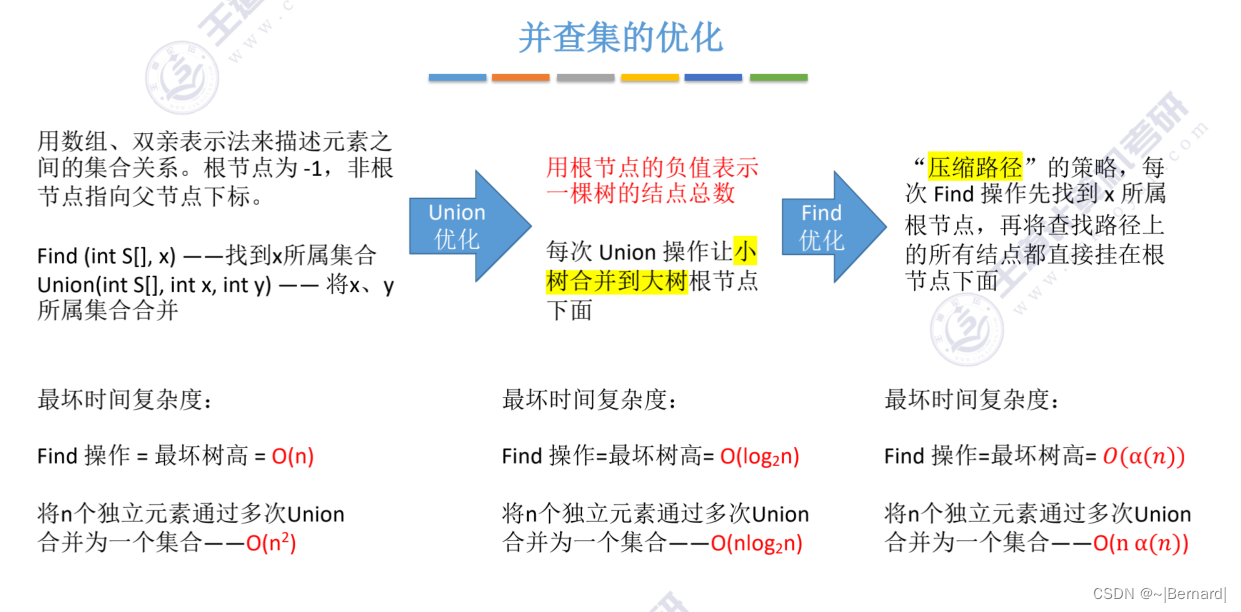 Union操作的时间复杂度都是用n个元素需要合并n-1次合并操作乘Find操作的时间复杂度得之
Union操作的时间复杂度都是用n个元素需要合并n-1次合并操作乘Find操作的时间复杂度得之