A / B测试在各个行业中有许多应用。从试图确定最佳市场群体到医疗药物测试，它具有各种应用，并允许企业根据结果做出决策。有两种常见的A/B检验方法，频率主义方法和贝叶斯方法，两者都是从假设检验的基础出发的。在本文中，我将介绍贝叶斯 A/B 测试方法的解释和实现。本文假设您对 A/B 测试在实践中有一个很好的了解，如果没有，您可以在此处了解有关它和频率主义方法的更多信息。

目录

• 贝叶斯方法
  -贝叶斯机器学习
• 贝叶斯 A/B 测试
  - 探索漏洞利用困境
• 问题陈述
• 贝叶斯强盗/汤普森采样-贝叶斯定理
  
  -贝塔分布
• 实现
• 结束语
• 资源

一、贝叶斯方法

        贝叶斯方法源于一个主要规则，即一切都是随机变量。例如，如果给定某个数据集，并且要求您查找数据的均值和方差，则输出将只是映射到平均值的数值和映射到方差的数值。但是，在贝叶斯方法中，您不再寻找数字，而是寻找分布。

<span style="background-color:#f2f2f2"><span style="color:#292929">When trying to identify the mean, you can see the difference of approaches below : 
Frequentist : ῦ
Bayesian    : p(ῦ | data)</span></span>

贝叶斯机器学习

如果你从机器学习的角度考虑这个问题，那么你可以看到A / B测试在直觉上与强化学习非常相似。强化学习是指允许智能体在环境中采取行动，以最大化奖励的概念。A / B测试可以被视为一组随机实验，其中随机分区的用户以最大化一些奖励。

例如，如果我们要使用A / B测试对网站上两个按钮的点击率进行建模，则可以将具有不同按钮的不同布局定义为一个操作，并且增加的点击率可以作为奖励。我们希望选择一个能够最大限度地提高点击率的布局。

二、贝叶斯 A/B 测试

        给定一些数据，贝叶斯过程可以通过以下步骤[1]概述：

1. 识别先验分布（高斯分布、泊松分布、β 分布等），这表示我们在查看任何数据之前对参数（例如 ῦ）的初步理解
2. 选择一个统计模型（马尔可夫链、贝叶斯强盗等），它反映了我们对给定 x 的信念 ῦ
3. 观察一些数据后，更新我们的信念并计算后验分布p（ῦ | x）。后验分布是一种概率分布，它描绘了您在观察数据后对参数的更新信念。

        可以想象，观测值 （N） 的数量越大，后验分布的近似越好。但是，如果您的观察次数过多，您将失去大量展示次数，从而为您的网站带来收入。例如，如果您正在为您的网站运行A / B测试，以确定哪个（两个）着陆页产生非常高的点击率，那么您做的样本越多，您向着陆页展示的人就越多，这将减少点击次数，您可能会获得点击次数。因此，具有不太大也不太小的样本量是理想的。

        探索漏洞利用困境

        在强化学习中，当智能体通过评估可能导致积极结果的场景来收集信息时，称为探索。 在探索之后，人们会根据当前已知的信息学习具有最高结果的最佳决策，称为利用。 最好平衡剥削和剥削。

三、问题陈述

        假设您要测试在平台上创建用户的两种不同位置。您的位置 1 位于网站的左上角，而位置 2 位于右上角。两个着陆页之间的唯一区别是注册按钮位于两个不同的位置，其他一切都相同，我们的实验是 iid。

3.1 贝叶斯 /汤普森采样

        在我们探索贝叶斯匪算法之前，我们需要对贝叶斯定理和贝塔分布做一些回顾。

        贝叶斯定理

        本质上，后验~可能性*先验

3.2 测试版分布

        这是一个连续概率分布，以区间 [0， 1] 为界，取决于两个参数α和β。 α和β都必须是符号为正的。在不涉及算术的情况下，β分布的PDF可以通过以下等式建模：

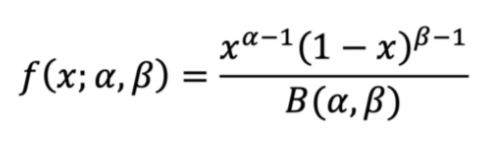
        有关更全面的解释和推导，请访问此处的维基百科页面以获取测试版。

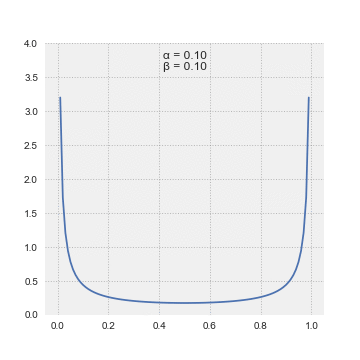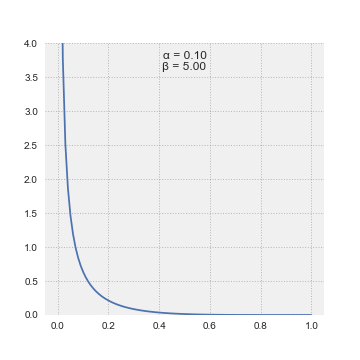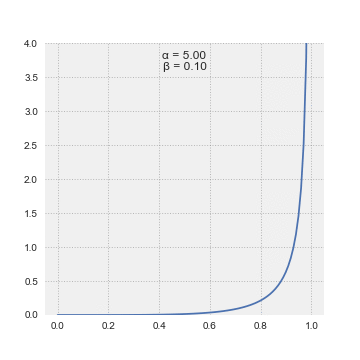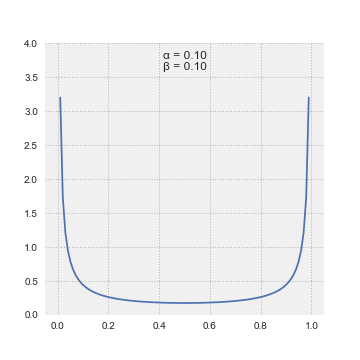
        此动画显示了其参数 alpha 和 beta 的各种值的 beta 分布如何变化。来源：来自维基百科的Pabloparsil

        现在我们可以探索贝叶斯土匪/汤普森采样算法。出于本实验的目的，假设我们知道排名 1 和排名 2 中每个位置的点击率概率。当然，在现实世界的例子中，这不会发生，但为了评估我们的算法在这种情况下的表现，假设和p(pos1) = 0.1p(pos2) = 0.55

        由于我们没有任何现有的观察，所以我们不可能有任何先验的信念。为了模拟我们的先验概率，我们可以对 α = 1 和 β=1 使用 beta 分布。这将是 [0，1] 域上的均匀分布。我们选择均匀分布是因为我们不知道结果可能是什么，因此我们对每个可能的值给出相等的概率。请注意，对于行业方案，如果您有可用的先验知识，则应在实现中使用该先验知识。

        对于这种方法，一步中的后验在下一步中成为先验，我们的后验和先验都可以通过 beta 进行建模。

                        <strong> Beta * Data = Beta</strong>
                         |____|        |____|
                         prior         posterior

四、实现

        请注意，由于分布的随机抽样，您的实现的结果可能会略有不同。

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import beta

# constants
true_proba = {'L':0.1,'R':0.55}
num_trials = 1000
trial_list = [50, 250, 500]

class BayesianBandit(object):
    def __init__(self, p, alpha = 1, beta = 1, N = 0):
        '''
        params:
            p (Float) : probability bounded between 0 and 1
            alpha (Float) : alpha of the beta distribution, default of 1
            beta (Float) : beta of the beta distribution, default of 1
            N (Integer) : tracks the number of trials, default of 0
        '''
        self.p = p
        self.alpha = alpha
        self.beta = beta
        self.N = N

    def simulate_action(self):
        '''
        This function will simulate the real world of users clicking or different versions of the website.
        '''
        return np.random.random() < self.p

    def sample(self):
        '''
        This function draws a sample from the beta distribution
        '''
        return np.random.beta(self.alpha, self.beta)

    def update(self, x):
        '''
        This function will update the alpha, beta and N for every iteration
        '''
        self.alpha += x
        self.beta += 1 - x
        self.N += 1

def plot(bandits, trial):
    '''
    This function will help visualize the distributions associated to each version
    of the website. It helps in compraison of which version is better.
    
    params:
        bandits (Object) : defined by the BayesianBandit class
        trial (Integer) : number of trials
    '''
    x = np.linspace(0, 1, 200)
    for b in bandits:
        true_prob = b.p
        win_rate = (b.alpha - 1) / b.N
        y = beta.pdf(x, b.alpha, b.beta)
        plt.plot(x, y, label="True p: {}, win rate = {}".format(true_prob, win_rate))
    plt.title("Distributions after {} Trials".format(trial))
    plt.legend()
    plt.show()
    
def experiment():
    bandits = [BayesianBandit(p) for p in list(true_proba.values())]
    
    rewards = np.zeros(num_trials)
    
    for i in range(num_trials):
        # Thompson sampling
        j = np.argmax([b.sample() for b in bandits])

        if i in trial_list:
            plot(bandits, i)

        x = bandits[j].simulate_action()

        # update rewards
        rewards[i] = x

        # update the distribution
        bandits[j].update(x)

    # print total reward
    print("total reward earned:", rewards.sum())
    print("overall win rate:", rewards.sum() / num_trials)
    print("num times selected each bandit:", [b.N for b in bandits])

if __name__ == '__main__':
    experiment()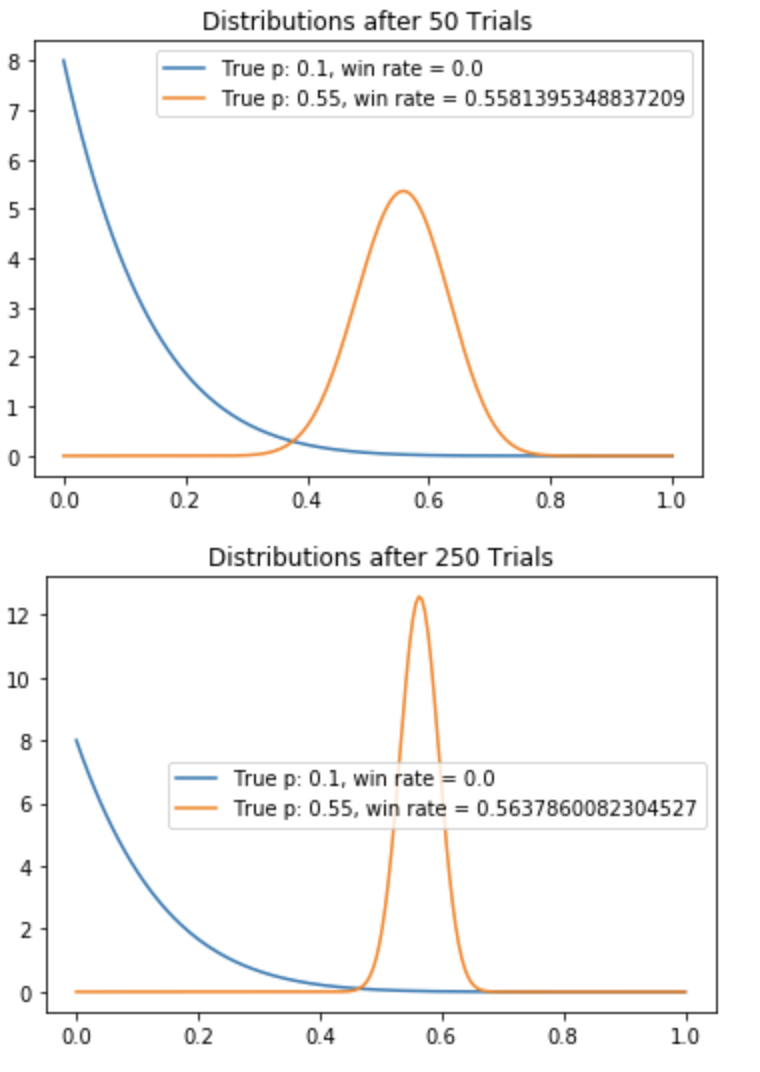

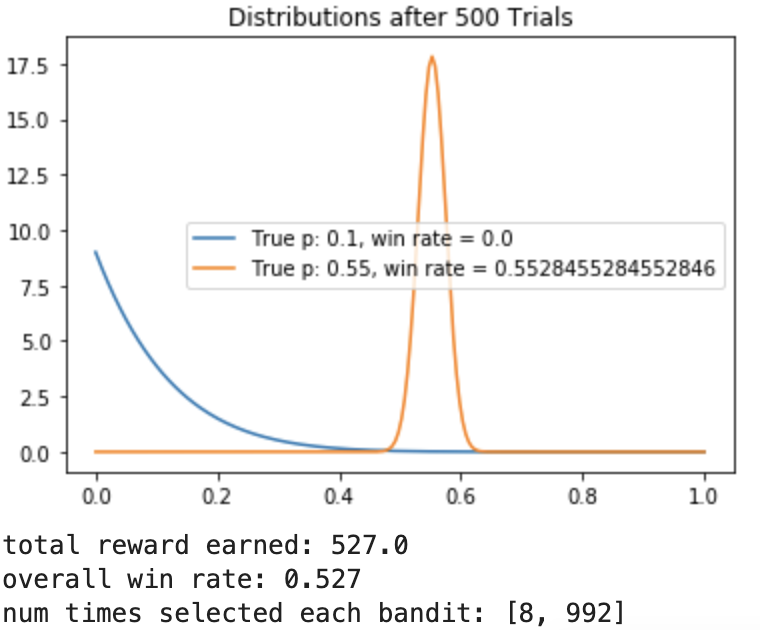
        如您所见，该算法会快速收敛到最佳分布。根据此实验的结果，很明显，排名 2 的表现优于排名 1，应该是您网站上注册按钮的位置。

五、结束语

        频率主义方法和贝叶斯方法之间的主要区别在于贝叶斯将参数视为随机变量。使用贝叶斯方式进行 A/B 测试的步骤是确定您的先前分布，选择一个统计模型并计算和更新您的后验分布。通常，贝叶斯A/B测试方法比其他传统的A / B测试收敛得更快。这意味着需要较小的样本才能得出结论。