机器学习-sigmoid函数和relu函数-个人解读

今天博主来解读一下sigmoid函数和relu函数，我觉得很多同学可能都知道这两个函数是什么，他们干什么的，他们有什么用，但是呢？我想这两个常用的激活函数内在的本质，很多同学应该不是很理解，今天博主就给出自己的一些解读。

首先，我们先谈谈激活函数是什么：

激活函数（Activation Function）是一种添加到人工神经网络中的函数，旨在帮助网络学习数据中的复杂模式。类似于人类大脑中基于神经元的模型，激活函数最终决定了要发射给下一个神经元的内容。
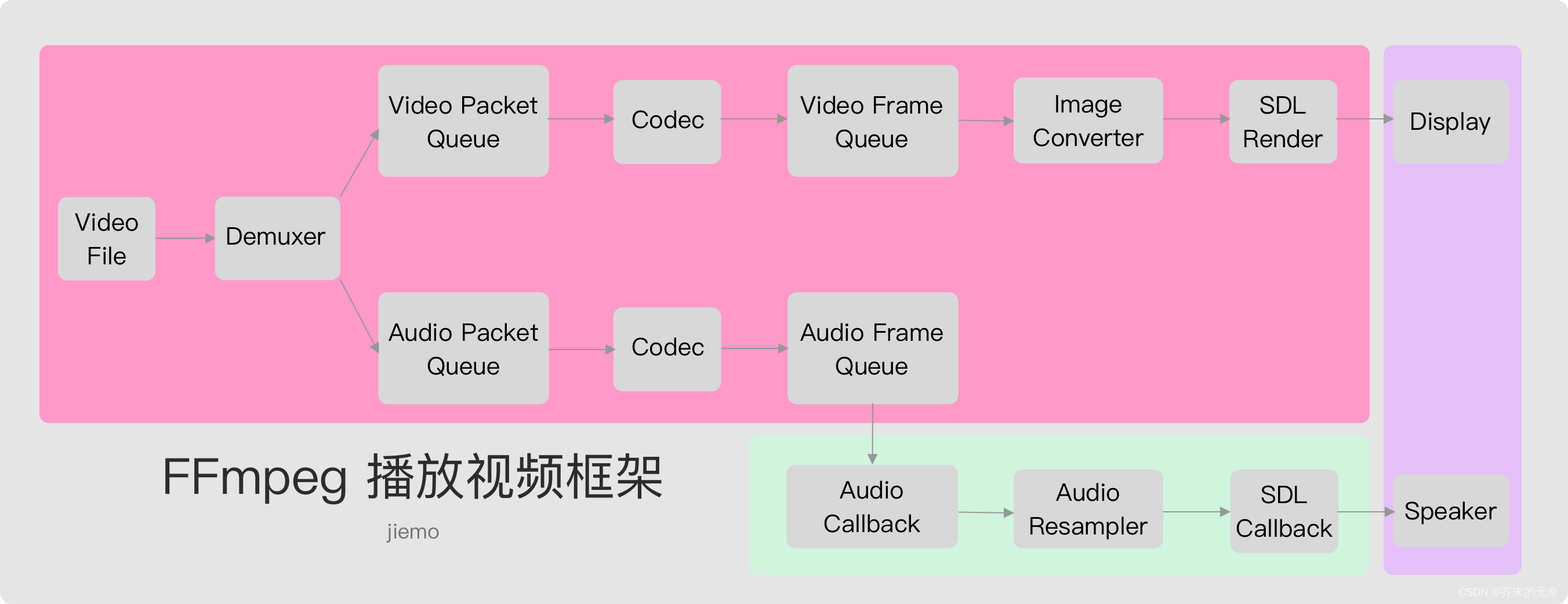
看下面一张图，图中博主标红的部分就是激活函数再一个单神经元的神经网络中的部分，它呢一般再深度学习中是对神经元的输出进行处理。
注：激活函数不仅仅再神经网络中应用，机器学习一些传统算法也很常用，再卷积神经网络中则是对卷积核的卷积输出进行处理。

然后，我们肯定要知道激活函数干什么的？（作用）
第一，读神经网络加入非线性激活函数后，由神经网络的万能定理，神经网络就可以拟合任何一个函数。也就是增强网络的表示能力。（下一个实验就是万能定理的实验）
第二，激活可以防止梯度消失、梯度爆炸且加快模型学习速度。

下面我们就介绍两种最常见的激活函数sigmoid函数和relu函数，并结合这两个函数解释一下为什么激活函数可以由上面两点作用。
首先是sigmoid函数：
数学表达式：

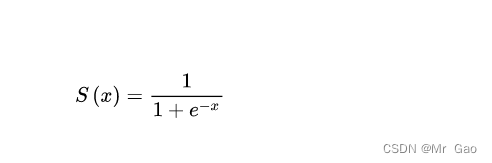
数学图像：

这里，我给出大家分析激活函数的方法，如何分析一个激活函数?
看下面几个激活函数的特征：
（1）看他的取值范围
（2）看他的对称性
（3）看他的导函数曲线（或者说看他的函数陡峭性）

其中1和3一般是最重要的。

大家可以看到sigmoid的取值空间是多少？
（0，1）
所以因为sigmoid这一个特性，sigmoid经常被用于作为概率转化，不过这种转化一般适用于二分类，大家可以思考一下这个问题，多分类一般用softmax，另外呢如果是做概率转化，则经常用于最后一步对全连接层的输出进行处理。

然后呢，看他的函数对称性，大家可以发现sigmoid是关于（0，0.5）对称的，这恰好满足了它作为二分类概率转化的一个重要特征，概率转化激活函数必须是对称的，这符合现实需求，比如我们最终对特征处理后，因为一般样本提取过的特征，影响性事线性的，比如我们给了一个输入X,经过神经网络表征学习最后变成了X’,X‘经过全连接层的线性转化，变成了一个值，然后再经过sigmoid函数处理，我们知道，这个值可能为负，可能为正，为负则sigmoid处理后输出小于0.5，则判断为负样本，为正则sigmoid处理后输出大于0.5，判断为正样本。
那我们知道总不能输入一个值1，一个值-1，经过激活函数处理，变成了0.4和0.9吧，一般我们认为我们表征学习后的特征影响性是符合线性情况的。

然后是导函数曲线，导函数曲线其实是最重要的，这里可以发现sigmoid函数基本上是x在(-5,5)上导函数才稍微大一点，其他情况但函数基本为0，那这个有什么用呢？
举个例子：
一个二分类问题
加入现在我们由5个样本输入模型，经过网络层的处理，最后在经过sigmoid函数处理之前的数值输出分别为：
-1，1，3，100，-100，
五个样本真实的标签则是0，1，1，1，0
注：上面五个值经过sigmoid函数处理处理后，为分类为1的概率。

大家可以发现，这五个数值经过sigmoid处理后，可以发现100，-100对应的导数值基本趋于0，100输出的概率激活为1了。也就是对于这个样本模型输出效果已经很好了，那么导数正好趋于0，也就是这个样本不应该对模型有大的影响。-100经过sigmoid函数处理输出几乎为0了，效果也很好,也不需要根据这个样本更新模型了，但是-1，1，3，这三个值对应的概率还不是最好的接近0，1，1，正好倒数值也比较大，用于对模型进行较大程度更新。

所以大家如果很仔细的看我上面这个例子，就会发现sigmoid函数的精髓，对于模型已经分类效果不错的样本，sigmoid不会随意根据这个样本调整模型，对于模型分类效果不好的样本，采用sigmoid函数则会对模型进行较大程度的调整。这种模型调整策略是很棒的。且sigmoid对称性特性和0-1区间的取值，是的其可以用于较好的处理概率问题。
但是也可以发现sigmoid函数很容易发生梯度消失，在只要输入的值不在（-5，5）之间，几乎就是梯度为0了，这也就是为什么隐藏层不加入sigmoid函数，因为太容易发生梯度消失了，但是可以在全连接层使用这个函数。

对于sigmoid函数，其实博主希望各位能好好看看上面这个例子，sigmoid函数可以说因为自己的函数特征有了其优点，也有了其缺点。

下面我们讲一下relu函数：
数学表达式：

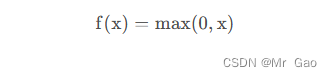
那么函数图像也很简单了：

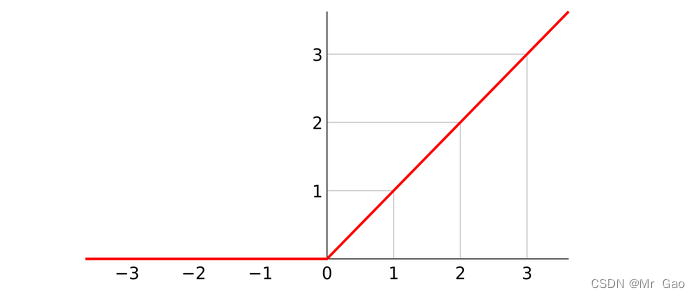
分析激活函数，还是先看它的下面三个特性：
（1）看他的取值范围
（2）看他的对称性
（3）看他的导函数曲线（或者说看他的函数陡峭性）

我们可以看到，它的取值范围是【0，正无穷】
而且根据输入激活函数随机性的原理我们可以知道，经过这个激活函数处理，有一般的概率输出为0，由反向传播的原理知道，经过激活函数输出为0，那么这激活函数在这次样本输入中其梯度就为0，也就是不会被更新，且该神经元的输出也不会对最终结果再有影响。这就形成了relu的稀疏性，就是指，relu处理后，由一般的概率会使当前神经网络层一半的的神经元失灵。很多同学可能就问了，哎呀，为啥要让他们失灵啊，那我们直接设置一半不就好了。

为什么relu要那么做呢，第一，神经网络学习能力是很强的，所以很容易过拟合，那么relu函数就可以一定程度解决这种问题。
第二，就是relu函数的真正精髓，每次训练会随机的让让很大一部分神经元失灵，只更新部分神经元，每次更新的部分神经元是随机的，在这种情况下，每次被更新的神经元组合是很复杂的，相同性很低，那么就可以有效的让神经元独立学习，孤军奋战，不那么被其他神经元影响，做出自己的有利贡献。博主觉得这才是relu函数的精髓，这可以大大提高模型的学习能力。

然后relu函数没有对称性就不看了，所以relu函数不能用于全连接层之后，都是用于隐藏层之后，对神经元学习有帮助。

然后再看其导函数，x>0导数都为1，不管x取什么值，只要x>1，否则倒数为0，x<=0也不用考虑，输出为0，神经元就失灵了，所以这个特性就是说明relu函数是为了神经元更新参数专门设置的，其不易发生梯度消失。只要输出有效，梯度就为1。