目录
💥1 概述
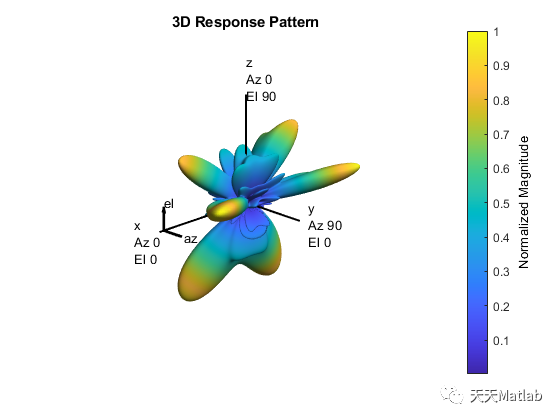
📚2 运行结果
🎉3 参考文献
👨💻4 Matlab代码
💥1 概述
车辆纵向动力学方面包括车辆传动系统换挡控制、制动系统的设计与控制以及车辆状态的参数估计;车辆横向动力学方面涉及车辆转向系统设计与横向稳定性控制;车辆垂向动力学方面包括悬架系统的优化设计与半/主动控制.专刊研究成果涉及车辆动力学与控制方向的多种问题,可为今后开展相关研究提供参考。
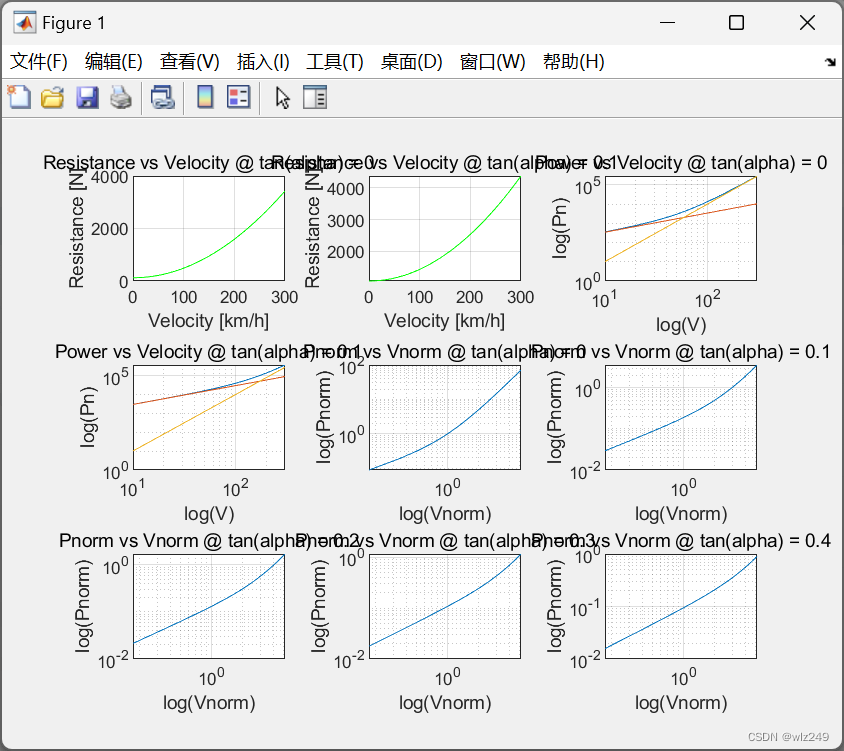
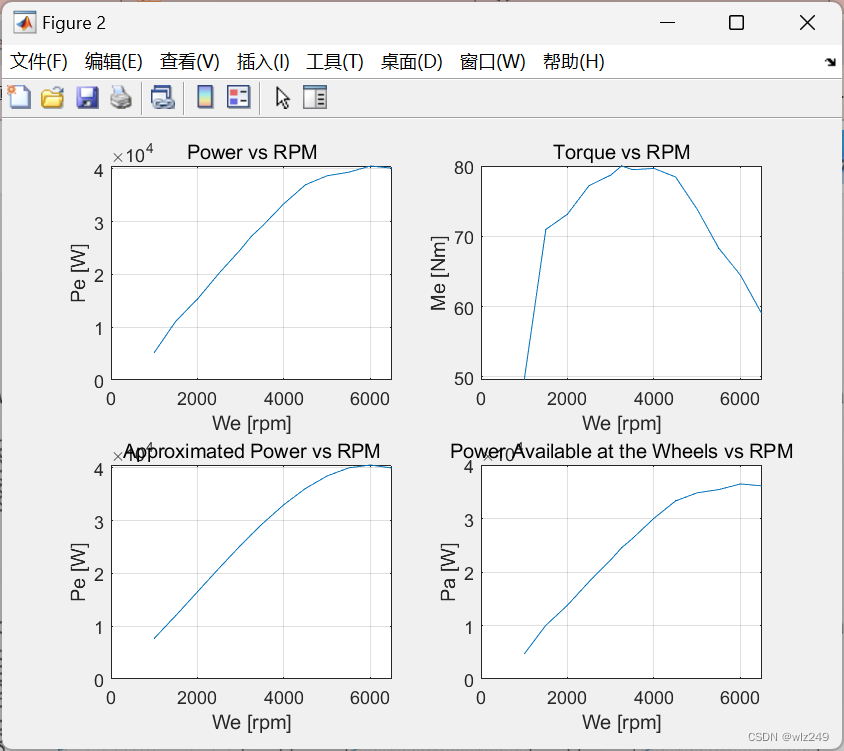
📚2 运行结果
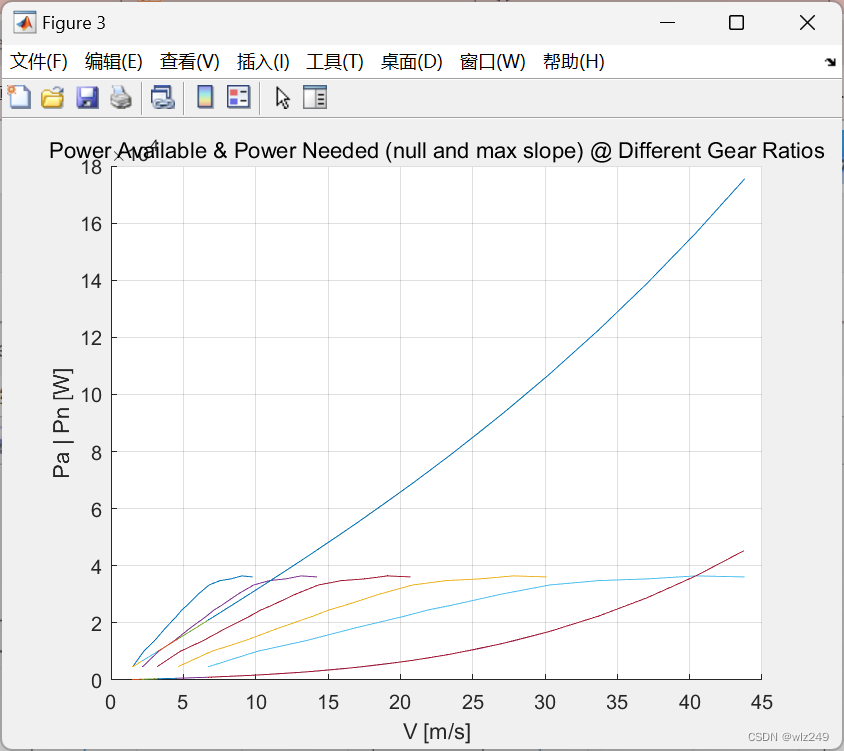

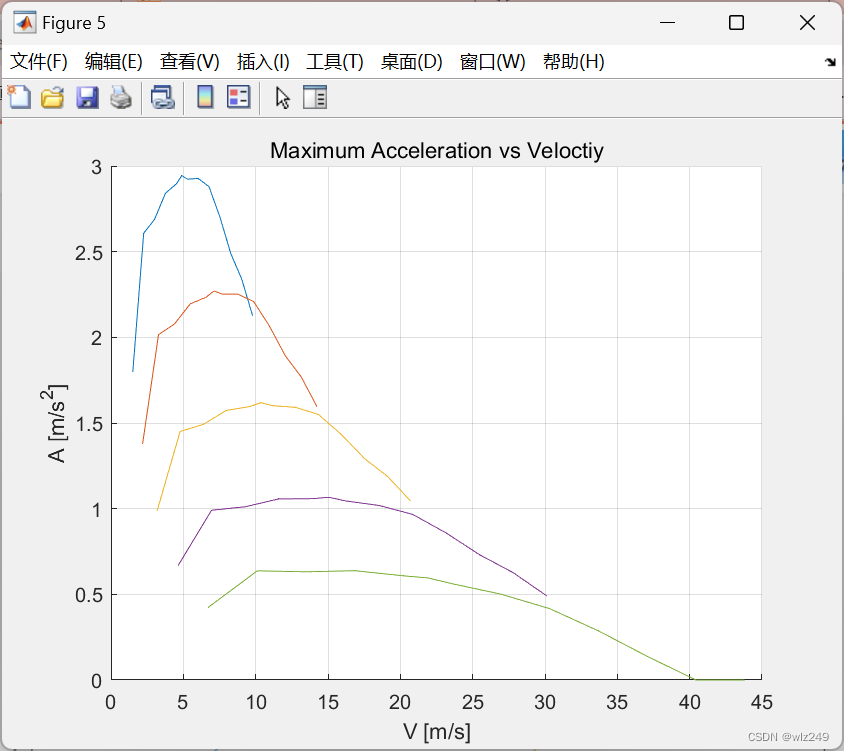
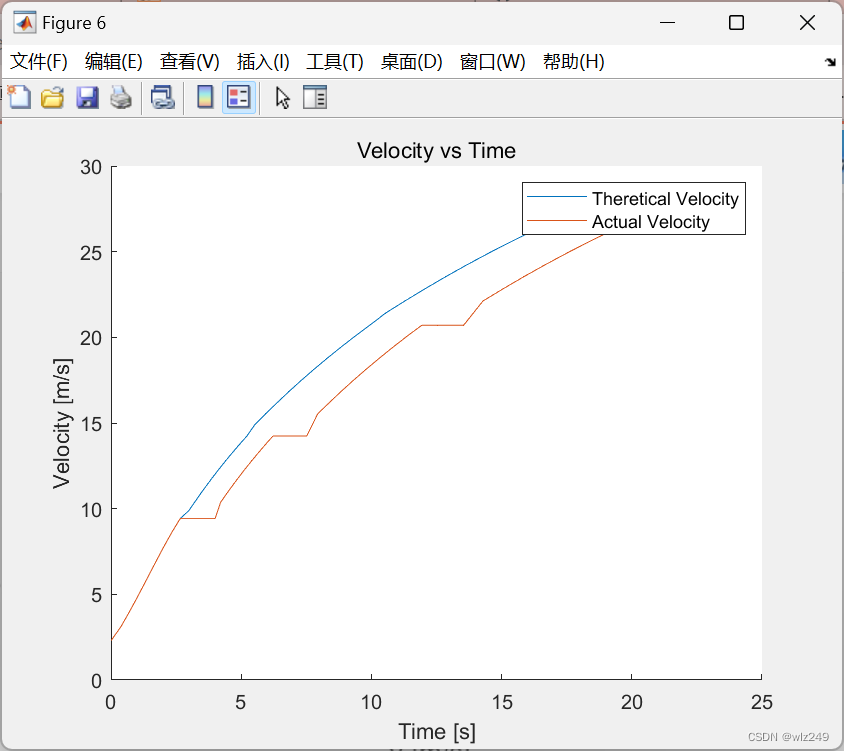
🎉3 参考文献
[1]李韶华,王伟达.车辆动力学与控制研究进展[J].动力学与控制学报,2021,19(03):1-4.
👨💻4 Matlab代码
主函数部分代码:
clear all
clc
%% Define Given Constants
Cx = .35; %[-] Aerodynamic Drag Coefficient
S = 1.82; %[m^2] Frontal Surface Area
m = 970; %[kg] Vehicle's Mass
Vcil = 1040; %[cm^3] Volume of Cylinder
Tf = .281; %[-] Differentail Transmission Ratio
wmin = 850; %[rpm] Minimum Engine Rotaional Speed
efficiencyt = .9; %[-] Efficiency of Powertrain
l = 2.3; %[m] Wheel Base
a = 1.15; %[m] Horizontal Distance From Center of Gravity -> Front Wheel
b=l-a; % [m] Horizontal Distance From Center of Gravity -> Rear Wheel
hG = .5; %[m] Height of Center of Gravity
wheel_indication = '155/65R13'; % Wheel Incdication
R0 = 13*25.4/2 + .65*155; %[mm] % Wheel Radius
Re = .98*R0*10^-3; % [m] % Wheel Effective Radius
N = 5; %[-] % Number of Gears
ts = 1; %[s] % Time of Shifting Between Gears
Je = .08; %[kg.m^2] Engine's Moment of Inertia
Jw = 1.6; %[kg.m^2] Wheels' Moment of Inertia
Jt = Jw; %[kg.m^2] Transmission's Moment of Inertia
g = 9.81; % [m/s^2] Gravitational Constant
ro = 1.3; %[kg/m^2] Air Density
alpha = atan(0:0.1:0.4); %[-] Angle of Inclination
f0 = .013; %[-] Rolling Resistance Coefficient 1
K = 6.51*10^-6; %[s^2/m^2] Rolling Resistance Coefficient 2
%% POWER NEEDED FOR MOTION
% Take Artbitrary Velocity Interval
vKm = 0:10:300; %[km/h]
vm = (vKm./3.6); %[m/s]
% Declare All Vectors/Matrices As Zeros
A = zeros(5, 1);
B = zeros(5, 1);
R = zeros(5, 31);
Pn = zeros(5, 31);
Pnorm = zeros(5, 31);
Pcar = zeros(5, 1);
Vcar = zeros(5, 1);
Av = zeros(5, 31);
Bv3 = zeros(5, 31);
% Calculate A, B, Vcar, Pcar, R, Av, Bv^3, Pn, Pnorm and Vnorm at 5
% different inclinations
for i = 1:5
A(i) = m*g*(f0*cos(alpha(i)) + sin(alpha(i))); %[N]
B(i) = m*g*K*cos(alpha(i)) + 0.5*ro*S*Cx; %[kg/m]
Vcar(i) = sqrt(A(1)/B(1)); %[m/s]
Pcar(i) = 2*A(i)*sqrt(A(i)/B(i)); %[W]
for j = 1:31
R(i, j) = A(i) + B(i)*(vm(j)^2); %[N]
Av(i, j) = A(i)*vm(j); %[W]
Bv3(i, j) = B(i)*vm(j)^3; %[W]
Pn(i, j) = Av(i, j) + Bv3(i, j); %[W]
Pnorm(i, j) = Pn(i, j)/Pcar(i); %[-]
end