---

第1章 引论

一些概念

1. 机器语言：以0、1代码表示的机器指令所构成的语言
   每一个具体的计算机系统都具有自己的指令系统

2. 汇编语言：用助记符来表示指令中的操作与操作数，同时用符号表示程序用到的一系列数据

3. 高级语言：C、C++、Java等

4. 编译程序(Compiler)：将源程序完整地转换成机器语言或者汇编语言程序，再处理、执行的翻译程序
   

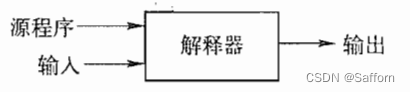
5. 解释程序(Interpreter)：边解释边执行的程序
   

6. 翻译程序：编译程序、解释程序、汇编程序、交叉汇编程序、反汇编程序、交叉编译程序、反编译程序、可变目标编译程序、并行编译程序、诊断程序编译程序、优化编译程序

1.3 编译程序的总体结构

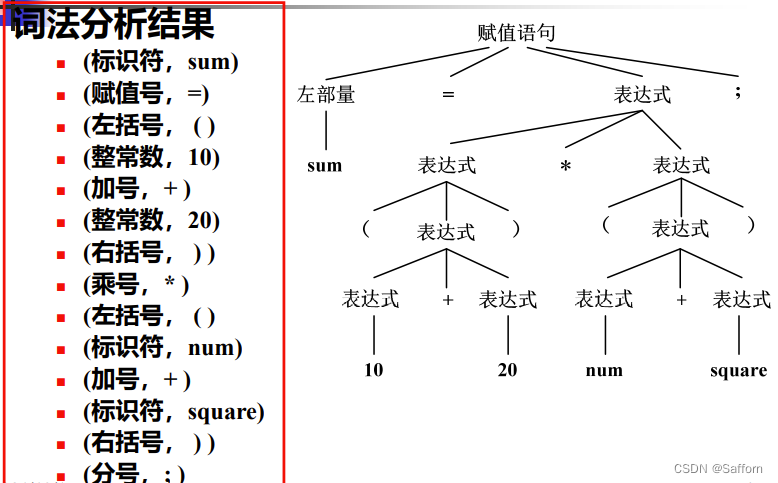
1. 词法分析
   输入：组成源程序的字符串
   输出：单词序列(token)
   词法分析器的功能：从左到右扫描组成源程序的字符串，并将其转化成单词串，将发现的标识符登记到符号表中，检查组词方面的错误并进行处理
   
2. 语法分析
   输入：单词序列
   输出：这些单词所组成的程序的结构(不同层次的语法成分)
   语法分析器的功能：“组词成句”，分层给出程序的组成结构，指出语法错误制导语义翻译
   
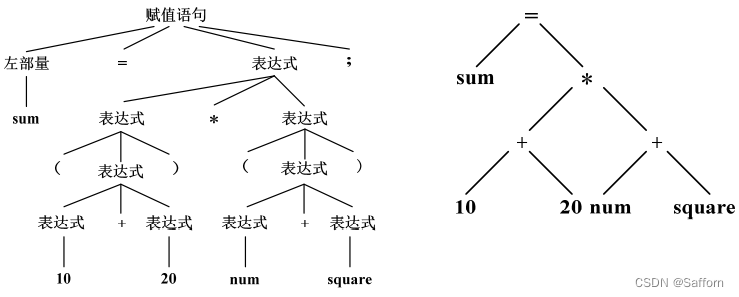
3. 语义分析
   通常在语法分析器分析出语法成分的同时进行该语法成分的语义分析，即语法制导翻译(syntex-directed translation)
   语义分析通常以中间代码的形式表达相应的操作过程
   功能：1）获取标识符的属性：类型、作用域等； 2）语义检查：运算的合法性、取值范围等；
   3）子程序的静态绑定：代码的相对地址； 4）变量的静态绑定：数据的相对地址
   
4. 中间代码生成
   以中间代码的形式实现对语义分析结果的表示
   特点：简单规范，与机器无关，易于优化和转换
   
5. 代码优化
   对中间代码进行优化处理，使程序运行能够尽量节省存储空间，更有效地利用机器资源，使得程序的运行速度更快，效率更高。（这种优化变换必须是等价的）
   分为 与机器无关的优化 和 与机器有关的优化

• 与机器无关的优化
  局部优化：

6. 目标代码生成
   为中间代码中出现的运算对象分配存储单元、寄存器等
   将中间代码转换成目标机上的机器指令代码或汇编代码
   $$目标代码的形式=\{\begin{array}{rl}& 具有绝对地址的机器指令\\ & 汇编语言形式的目标程序\\ & 模块结构的机器指令(需要链接程序)\end{array}$$

7. 错误处理
   进行各种错误的检查、报告、纠正，以及相应的续编译处理（如：错误的定位与局部化）
   词法分析阶段：拼写方面的错误误，出现非法字符等
   语法分析阶段：表达式、句子或程序结构等错误
   语义分析阶段：类型匹配错误、参数匹配错误、非法转移问题等

8. 符号表管理(表格管理)
   按照编译过程中的信息需求，以不同的类型组织符号表，并以合适的方式查、填、维护这些表格，提供信息服务，辅助实现编译任务

下图是编译程序处理赋值语句的翻译过程

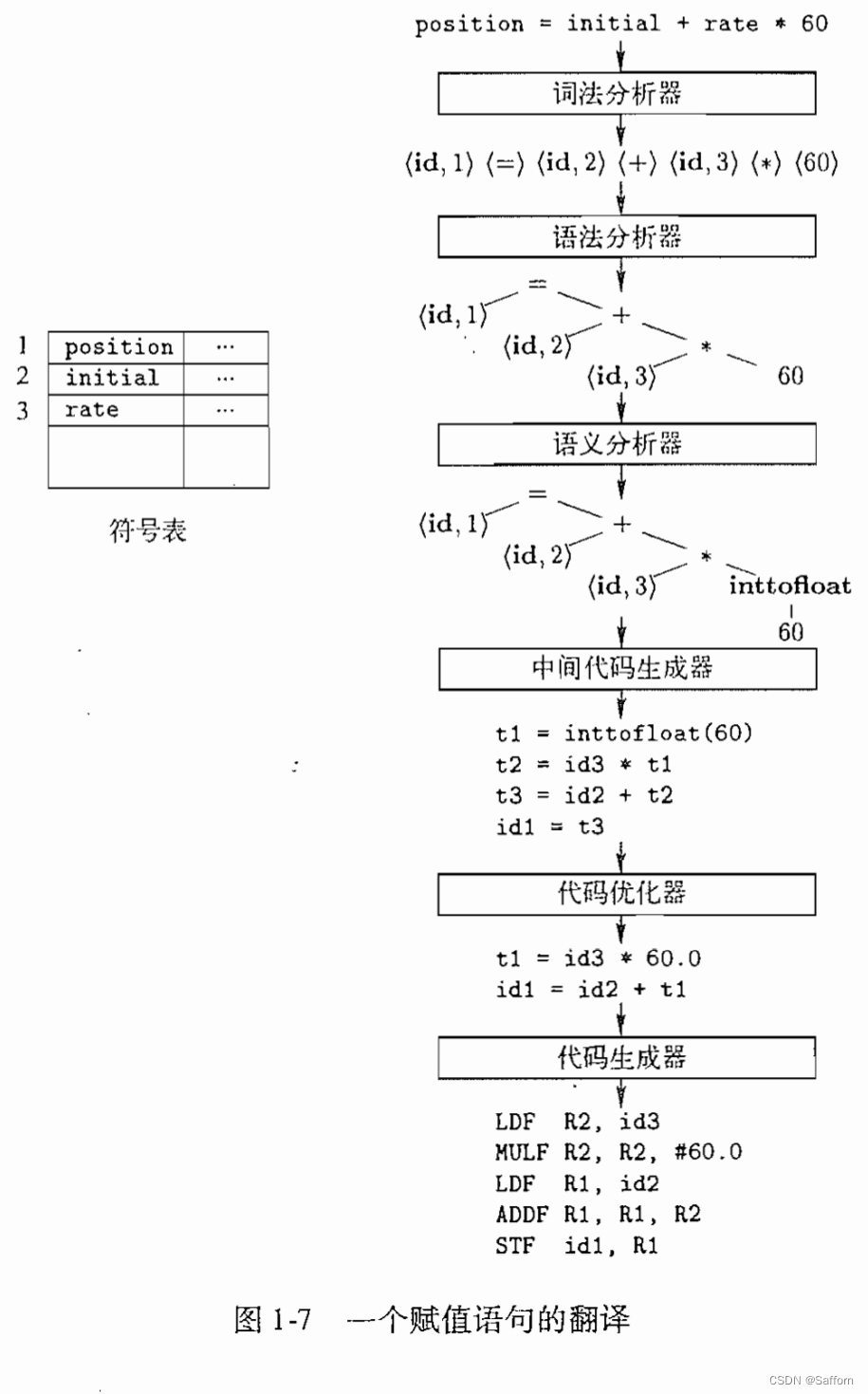
1.4 编译程序的组织

通常称编译程序对源程序或中间结果的完整扫描为 遍

第二章 形式语言

2.1 文法描述中的基本概念

1. 字母表：一个非空有穷字符集，记作 $\sum$
2. 字符：字母表中的每个元素称为 字符
3. $\sum$ 上的字：由$\sum$中的字符所构成的一个有穷序列
4. 空字 ε：不包含任何字符的序列
5. ${\sum }^{+}$：字母表$\sum$的正闭包，即${\sum }^{+}=\sum \cup {\sum }^1\cup {\sum }^2\cup ...$
6. ${\sum }^{\ast }$：字母表$\sum$的Kleene闭包，即${\sum }^{\ast }=\epsilon \cup \sum \cup {\sum }^1\cup {\sum }^2\cup ...$

示例：若 ∑ = { 0 , 1 } \sum = \{0,1\} ∑={0,1}，则 ∑ + = { 0 , 1 , 00 , 01 , 10 , 11 , 000 , . . . } \sum^{+} = \{0,1,00,01,10,11,000,...\} ∑+={0,1,00,01,10,11,000,...}， ∑ ∗ = { ε , 0 , 1 , 00 , 01 , 10 , 11 , 000 , . . . } \sum^{*} = \{{\color{red}{ε}},0,1,00,01,10,11,000,...\} ∑∗={ε,0,1,00,01,10,11,000,...}

${\sum }^{+}$ 与 ${\sum }^{\ast }$ 的区别：
如果 $\sum$ 中不包含空字$\epsilon \text{ε}\epsilon$，则 ${\sum }^{\ast }$ 中包含空字$\epsilon \text{ε}\epsilon$，而${\sum }^{+}$ 中不包含空字$\epsilon \text{ε}\epsilon$

7. 句子：$\forall x\in {\sum }^{\ast }$，$x$ 称为字母表 $\sum$ 上的一个句子，其中 $\epsilon \text{ε}\epsilon$ 称作 $\sum$ 上的空句子
8. 字符a的出现：$\forall x,y\in {\sum }^{\ast },a\in \sum$，句子 $xay$ 称为字符 $a$ 在该句子中的一次出现

上下文无关文法

1. 上下文无关文法 G 为一个四元组，即 $G=(V_T,V_N,S,P)$，其中：
   $V_T$：终结符集合（非空）
   $V_N$：非终结符集合（非空），且 $V_T\cap V_N=\varnothing$
   $S$：文法的开始符号，$S\in V_N$
   $P$：产生式集合（有限）
   每个产生式的形式为 $P\to \alpha ,P\in V_N,\alpha \in (V_T\cup V_N{)}^{\ast }$，读作 P 定义为 $\alpha$，P 是非终结符(也是被定义的句法单位)，$\alpha$ 是终结符和非终结符组成的串，利用了字符集上字的全体的记号
   规定：开始符号 S 至少在某个产生式的左部出现一次

示例：i 为 标识符(identifier)，E 为 表达式(expression)。定义只包含 + 和 * 的算术表达式的文法 G = < { i , + , ∗ , ( , ) } , { E } , E , P > G = < {\color{red}{\{i, +, *, (, )\}}}, {\color{green}{\{E\}}}, {\color{blue}{E}}, P> G=<{i,+,∗,(,)},{E},E,P>，其中 P 由下列产生式组成：E → i，E → E + E，E → E * E，E → (E)，各产生式的意义为 一个表达式可以由一个标识符、或 两个表达式相加、或 两个表达式相乘、或 被括起来的表达式 这四种形式组成。

2. BNF的产生式缩写
   即 E → i，E → E+E，E → E*E，E → (E)
   可以缩写为 E → E | E+E | E*E | (E)
3. 直接推导：称$\alpha A\beta$ 直接推出 $\alpha \gamma \beta$，即 $\alpha A\beta \Rightarrow \alpha \gamma \beta$，仅当 $A\to \gamma$是一个产生式，且 $\alpha ,\beta \in (V_T\cup V_N{)}^{\ast }$
   推导：若 ${\alpha }_1\Rightarrow {\alpha }_2\Rightarrow ...\Rightarrow {\alpha }_n$，则称这个序列为 从 ${\alpha }_1$ 到 ${\alpha }_n$的一个推导；
   若存在一个从 ${\alpha }_1$ 到 ${\alpha }_n$的一个推导，则 称 ${\alpha }_1$ 可以推导出 ${\alpha }_n$
   对于 G(E)：E → E | E+E | E*E | (E)，想通过E 推导出 (i+i) ，则可以的做法是 $E\Rightarrow (E)\Rightarrow (E+E)\Rightarrow (i+E)\Rightarrow (i+i)$
   

示例：每个确定的单词是一个终结符

分析：
<主语><谓语><间接宾语><直接宾语> 是一个 句型
He gave me <直接宾语> 也是一个 句型
He gave me a book 是一个 句子 ，全都由 终结符 组成
可以看出，句型 是 对某些结构相同的句子 的抽象
所以 这个文法的开始符号本身 <句子> 也是一个句型，而且 句子都是句型，但句型不一定是句子

4. 句型、句子、语言
   句型：假定 G 是一个文法，S 是 G 的开始符号。如果 $S{\Rightarrow }^{\ast }\alpha$，则 $\alpha$ 是一个句型
   句子：仅含 终结符 的句型 是一个句子
   语言：文法 G 所产生的句子的全体 是一个 语言，记作 L ( G ) = { α ∣ S ⇒ + α , α ∈ V T ∗ } L(G) = \{\alpha | S\Rightarrow^{+}\alpha, \alpha \in V_T^* \} L(G)={α∣S⇒+α,α∈VT∗​}