线性规划是运筹学的基础，在现实企业经营中，如何有效的利用有限的人力、财力、物力等资源。                   

MATLAB

为方便大家理解，这里我们直接用一个例题为大家讲解使用matlab求解线性规划问题。

根据上图给出的线性规划问题。我们使用linprog函数解线性规划需要满足：

首先，我们的目标函数是为最小值，如果是最大值那么改变其正负号转为最小值。

其次，需要将其约束条件中(大于等于)转化为(小于等于),还是要注意转换正负号。

最后，等号方程不变。如下图：

 这时候，我们再使用linprog函数：[x,fmin] = linprog(f,A,b,Aeq,beq,lb)

%%
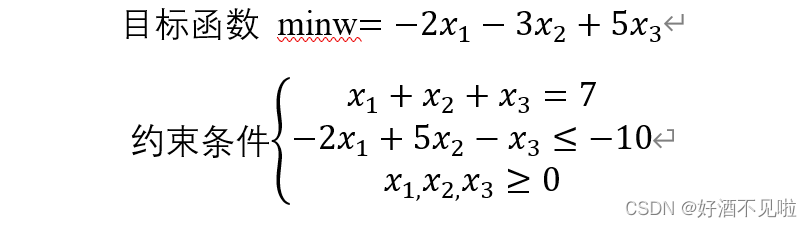
f=[-2,-3,5]';     %f为目标函数系数矩阵（注意后面的'在MATLAB中为转置的意思）
A=[-2,5,-1];      %A为系数矩阵小于等于部分的矩阵
b=[-10]'          %b为约束右边项矩阵（注意转置符号）
Aeq=[1,1,1]       %Aeq为等式方程的系数矩阵
beq=[7]           %beq为等式方程的约束右边项矩阵
lb=zeros(3,1)     %zeros（3，1）为约束条件，即三个变量均大于0，在MATLAB中是输出3行1列的0矩阵
[x,fmin]=linprog(f,A,b,Aeq,beq,lb);
fmax=-fmin        %linprog输出的fval为最小值，因此我们变号，将其改为最大值
x,fmax            %最后输出x的最优解，以及目标函数的最大值
%%

注意：矩阵的转置问题 ！！那个矩阵进行了转置，那些没有，大家一定要看清楚。

对于matlab中的线性规划问题大致就是这样，大家根据上面所举的例题照葫芦画瓢基本上不会出错。

许多时候，我们的运输问题也可以通过linprog()进行求解,感兴趣的可以自行尝试，在这里就不给大家放上去了，如果有需要的可单发。

补充

MATLAB方面呢，更多的会推出一些可直接食用的计算代码，例如关于本章的线性规划问题的求解以及接下来推出的二元一次方程、常微分方程的求解、积分求解、峰度、偏度等等。既方便读者，同时也方便我自己将来使用。大家如果有需要其他的问题解法，也可以告诉我，尽力帮你解决。

小白上路，相互探讨、相互进步。