深度学习入门知识总结

0、前言：学习了深度学习入门的鱼书，很多基础概念有了大概了解，及时总结，方便日后查找

1、神经网络（深度学习）的起源算法——感知机：

定义：感知机接收多个输入信号，输出一个信号，这里的信号理解为电流或者河流具备流动性的东西。感知机信号只有1/0两种取值（流/不流）
用感知机可以实现“与门、与非门、或门”，但是无法直接实现“异或门”
感知机的局限性就在于它只能表示由一条直线分割的空间
可以通过“与门、与非门、或门”叠加实现异或门，以下是2层感知机实现“异或”门
多层感知机的作用巨大：理论上用两层感知机就可以实现计算机的功能，感知机通过叠加层能够实现非线性表示。多层感知机就可以看作是神经网路了。
激活函数：将输入信号的总和转换为输出信号，在神经网络中，使用的除阶跃函数以外的其他函数作为激活函数，激活函数是连接感知机和神经网络的桥梁。
- sigmoid函数：具有平滑性，对神经网络的学习具有重要作用！
- Relu函数
- 阶跃函数
神经网络中使用的激活函数是平滑变换的sigmoid函数，感知机中使用的激活函数是阶跃函数。

2、神经网络：

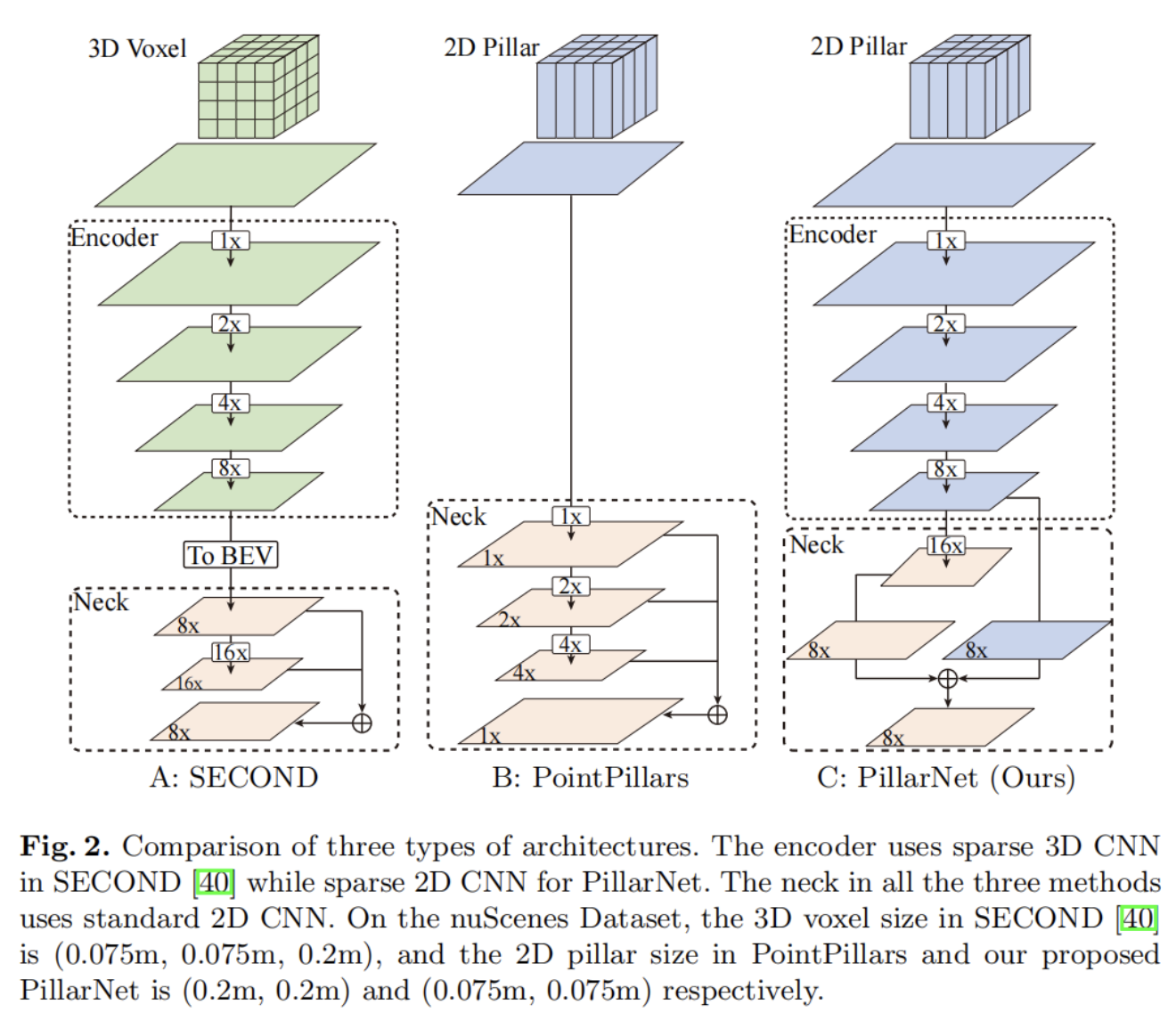
如下图所示是一个三层神经网络：
在神经网络中每一层传递的都是数组，借助python中数组运算的特性（numpy库）就可以实现数组在每一层的运算和传递。
输出层激活函数的设计：二元分类问题使用sigmoid函数，多元分类问题使用softmax函数，回归问题使用恒等函数。
求解机器学习问题的步骤分为：
- 学习：进行模型的学习
- 推理：用学到的模型对未知的数据进行推理（分类）
- 注意：一般在推理阶段输出层不用加激活函数，只有在学习阶段才需要给输出层加激活函数
手写数字识别的神经网络模型：
- 1、输入：因为数据集中每个图片大小是28X28=784个像素，所以输入层就是784个
- 2、输出：因为分类结果是从图片中识别结果是0-9，所以输出层为10个
批处理：每次输入的数据是通过批处理实现的，上面的例子已经可以理解输入到手写数字识别中的数据是784个，这是一张图片的数据压缩为了一个一维数组输入的，一次输入到模型中的如果只有一张数据是比较缓慢的，所以有了数组的概念，就可以一次输入一批图片进去，比如一次输入100张图片，那么输入数据就是一个100行784列的二维数组。最后结果就是一个100行10列的二维数组，如下图所示是数据进入模型之后的运算过程（变形过程）：

通过批处理就能实现高效的运算。

3、神经网络的学习阶段：

定义：神经网络的学习指的是从训练数据中自动获取最优权重参数的过程，为了使神经网络能进行学习，就需要应用到损失函数作为指标。学习的目的就是找出使损失函数达到最小的权重参数，这个过程就可以用梯度法来实现。找到了合适的权重参数，模型就算是训练完成，就可以用来解决分类或者回归问题了。
神经网络（深度学习）的优点：通过机器来学习特征，减少了人工参与，神经网络是端到端的学习。
机器学习中的数据划分为两部分：
- 训练数据：也叫做监督数据，用来寻找最优参数。
- 测试数据：用来评价模型的泛化能力，也就是说通过训练数据训练的模型（有了最优参数），如果在训练数据中准确率很高，但换成测试数据之后，准确率就下降了，这种现象叫做过拟合。如果得到的模型不光在训练数据中准确率高，在测试数据中准确率也很高，那就可以说模型的泛化能力很好。
损失函数：可以使用任意函数，但一般是均方误差和交叉熵误差。举个例子，用均方误差作为损失函数，如下图，可以明显看到，损失函数越小，模型输出的结果越接近真实值。
mini-batch学习：要判断模型的损失函数，就需要求出所有训练数据损失函数的平均值，如果训练数据比较多，那计算一次损失函数很慢，不现实，所以可以从全部训练数据中选出一部分来近似。例如从60000个训练数据中随机选100个，然后用100个进行学习，这种学习方式就叫做mini-batch学习。
总结：在神经网络学习中，寻找最优参数（权重和偏置）时，要找到使损失函数值尽可能小的参数。为了找到使损失函数尽可能小的地方，就要计算参数的导数（梯度），通过导数作为指引，逐步更新参数的值。
对权重参数的损失函数求导原理：将参数视为变量，对关于参数的函数求导，如果导数为负数，说明损失函数关于参数递减，所以参数值增加，损失函数的值变小。如果导数为正数，说明损失函数关于参数递增，所以参数值减小，损失函数的值变小。注意，当导数的值为0时，权重参数不影响损失函数的变化。
两种求导方式在深度学习中的应用：
- 数值微分：通过导数的定义求导数
- 第二种用误差反向传播法，相当于用了导数计算公式（可以高效地计算））
- 一般数值微分用来检验误差反向传播是否计算正确，这个过程也叫“梯度确认”。
- 注意在深度学习中参数很多，所以一般是采用链式法则求偏导。
梯度：由全部变量的偏导数汇总而成的有方向的向量称为梯度。梯度的大小就是函数减小的缓慢程度，梯度的方向就是函数减小的方向。梯度表示的是各个点函数值减小最多的方向，
- 函数的取值沿梯度方向前进一定距离，然后在新的地方重新求梯度，再沿着梯度方向前进，如此反复，逐渐减小函数值的过程就是“梯度法”，找函数最大值的梯度法叫做“梯度下降法”，找函数最小值的方法叫做“梯度上升法”。在深度学习中常用“梯度下降法”。用数学式来表示梯度法如下，下面的x0和x1就可以看作两个参数，如果有多个参数，道理也是一样：
学习过程的实现：
1、从训练数据中随机选择一部分数据（mini-batch）,目标是减小mini-batch的损失函数的值。
2、计算损失函数关于各个权重参数的梯度。
3、将权重参数沿梯度方向进行微小的更新。
4、重复1，2，3
注意：随机梯度下降算法（SGD）中随机指的是mini-batch的数据是随机选择的。

4、相关学习技巧：

参数更新
- “最优化”：神经网络的学习目的是找到使损失函数的值尽可能小的参数，这是寻找最优参数的问题，解决这个问题的过程就是最优化。
- 常见的参数最优化方法：
  - “随机梯度下降法”：简称SGD，这个方法就是为了寻找最优参数，将参数的梯度（导数）作为线索，沿着梯度方向更新参数。
    -“Momentum”：模仿物理学中加速度概念的方法
  - “AdGrad”：会随着参数变化调整学习率
  - “Adam”：结合了Momentum和AdGrad两种方法的优点
权重初始值
- 在神经网络学习中，权重初始值的设置非常重要。
- 权重初始值的生成必须随机化，但要合理，初始值设置不当，就会出现梯度消失的问题，一般在深度学习框架中，Xavier初始值已被作为标准使用。
- 小结：实践表明，当激活函数使用ReLU时，权重初始值使用He初始值，当激活函数为sigmoid或tanh等S型曲线函数时，初始值使用Xavier初始值。
添加Batch Normalization层
- Batch Normalization层定义：向神经网络中插入对数据分布进行正规化的层
- 优点：
  - 可以使学习快速进行（可以增大学习率）
  - 不那么依赖初始值
  - 抑制过拟合
超参数：
- 定义：超参数包括（各层中神经元的数量、batch大小、参数更新时的学习率或权值衰减等。），超参数也可以影响模型的效果
- 验证数据可以用来评估超参数的好坏，如果使用测试数据来评估超参数的好坏，就可能会造成过拟合，验证数据是验证超参数专用，不同于训练数据和测试数据
- 数据划分：
  - 训练数据：用于参数（权重和偏置）的学习
  - 测试数据：用于测试模型准确度
  - 验证数据：先从训练数据中获取20%的数据作为验证数据，目的是用于测试超参数
过拟合解决办法：
- 定义：过拟合指的是只能拟合训练数据，但不能很好的拟合不包含在训练数据中的其他数据的状态。
- 抑制过拟合的方法：
  - 1、权值衰减：通过在学习过程中对大的权重进行惩罚，来抑制过拟合。
  - 2、Dropout：在学习的过程中随机是删除神经元的方法。
卷积神经网络：
- 简称CNN，常被用于图像识别、语音识别等各种场合。
- CNN相对于之前介绍的全连接层，优点是可以利用与形状相关的信息，之前通过全连接层对手写数字图片识别时，是将图片的每个像素组成的二维数组拉伸为了一维数组，然后进行深度识别，这种就是全连接层的方法，而CNN可以输入一个二维或者三维数组来保持形状相关的信息。
- CNN中滤波器的参数就相当于全连接的神经网络中的权重，CNN中的偏置通常只有一个
- 卷积：卷积（Conv）运算就是输入数据与滤波器进行的对应相乘后求和的运算，也会变小
- 池化：池化（Pooling）就是从目标窗口获取最大值（或平均值），池化处理之后，高和长方向都会变小