目录标题
- 位图的优缺点
- 为什么会有布隆过滤器:
- 布隆过滤器的应用场景:
- 布隆过滤器的实现
- 布隆过滤器的测试
位图的优缺点
位图的优点:
1.位图可以节省空间,位图判断存储的数据是在还是不在只用一个比特位就可以记录数据出现的情况,而红黑树和哈希表储存一个数据是否出现则需要消耗很多的额外空间。
2.位图处理数据的效率非常的高,只用o(1)的时间就能判断数据存在的结果,相较于红黑树在某些方面效率更高。
位图的缺点:
1.一般要求数据的范围相对集中,范围如果特别分散的话,空间额度消耗就会上升。
2.只能针对整形数据,对于其他类型的数据就不是那么的适用。比如说浮点数类型,它的数目就比正数多的多,所以浮点数类型使用位图来进行存储就有点不那么合适。
为什么会有布隆过滤器:
如果我们想要记录字符串是否出现的话这里也可以使用位图来进行记录,位图只能针对整形的数据来进行存储,字符串不是整形所以要想存储字符串就得使用哈希函数来进行转换,将一个字符串转换成为一个整数,这样我们就将一个字符串转换成为一个整数来进行存储,但是这么搞还是存在一个问题,字符串拥有无限个,但是整形只有有限个,所以使用这样的方法来进行标记肯定会出现问题,比如说字符串aceg和字符串bdfh通过哈希函数转换成为的整型数字是一样的,那么这个时候在使用位图的时候就会出问题,我本来没有插入aceg但是因为之前插入了bdfh所以我在查找aceg的时候他也会告诉我该数据存在,但是实际是不存在的,所以这就是之前实现位图时会出现的问题,如果标记的地方为0就说明数据肯定是不在的并且没有误判,但是如果查找的地方为1的话就说明当前的数据是可能存在的但是可能会误判,那么为了优化这个问题有人就提出来了布隆过滤器这个东西,他就是多使用几个哈希函数进行映射,这样的话虽然会用碰撞,但是只要这几个哈希函数对应的位置有一个为0的话就说明当前的数据不存在,比如说下面的图片

当前存在10个比特位,布隆过滤器有三个哈希函数,所以我们每存储一个数据就会将三个比特位赋值为1,比如说字符串abcd通过布隆过滤器转换成为的值是4 5 6,因为4 5 6位置上的值都是0所以当前数据是不存在的,所以将这几个位置上的值变成1即可,比如说下面的图片:

然后这个时候还要存储字符串bcde,这个字符串转换的整型是2 3 4 ,因为2和3位置上的值为0所以当前的数据是不存在的,那么将2 3 位置上的值变成1 即可,那么这里的图片就如下:

当我们还要存储数据 cdef时,该字符串对应的整型时3 4 5 因为这3位置上没有一个位置是0,所以我们认为当前的数据是存在的直接插入失败,但是该字符串真的存在吗?不一定对吧,他是因为哈希冲突而误认为的存在,所以布隆过滤器不能完全的解决问题,但是能够优化数据冲突的概率。那么这就是布隆过滤器,它映射多个位置,降低误判率,但是这里的映射不是越多越好,因为映射的越多效率就越低,占用的空间也就越多,那么这就是布隆过滤器的原理希望大家能够理解。
布隆过滤器的应用场景:
1.布隆过滤器适用于一些不需要一定准确的场景
比如说注册昵称的时候需要判断这个昵称是否存在,那么这个时候就只用大致的判断的一下是否存在,如果不存在的话那是真的不存在,如果存在的话也可能是不存在,所以这里可能会出现错误但是我们不需要判断的那么准确,那么这里就可以使用布隆过滤器。
2.提高效率
比如说在客户端上面通过一个人的id从几千万个人的数据中查找对应的数据,首先输入的id可能是不存在的其次数据是存储在服务器的磁盘上面,而磁盘的访问是很慢的,而你输入的数据又可能是错误的,所以这样的话就会导致数据的访问效率特别的低,所以为了提高数据访问的效率我们就可以在访问数据库之前添加一个布隆过滤器,在往磁盘中查找之前先判断一下数据在还是不在,如果数据在的话就去磁盘中查找,如果数据不在的话就直接返回
布隆过滤器的实现
首先我们得判断一下布隆过滤器需要几个哈希函数,因为布隆过滤器含有多个哈希函数,一个数据也就会占用多个空间,那么我们在开辟空间的时候也就得多开辟几个空间用来存储数据,比如说原来只有一个哈希函数的时候存储100个数据需要100个比特位,但是现在有3个哈希函数那存储100个数据的时候是开辟300个比特位的空间还是400个比特位的空间呢?对吧虽然哈希函数越多越可以帮助我们解决哈希冲突问题,但是他消耗的空间是不是也就越多啊对吧,所以像这种问题我们一定能够得到一个公式,用多少个哈希函数开辟多大的空间能够使得效率最高,那么这个公式就是k =m*ln2/n,k表示哈希函数的个数,m为布隆过滤器的长度,n为插入元素的个数,当哈希函数的个数为3时m约等于4.2倍n,所以这就说明当我们插入一个数据的时候需要开辟4.2个空间才能使得误报率最小,所以这就告诉当哈希函数的个数为3时,布隆过滤器的长度得是插入数据的个数的4.2倍,那么这里为了简介我们将这里的4.2倍修改成为4倍即可,有了这个理论支持我们就可以模拟实现一下布隆过滤器,首先我们需要三个哈希函数能够将字符串转换成为整型,那么这里就不是我们的重点,所以直接给大家列出这三个仿函数:
struct BKDRHash
{
size_t operator()(const string& key)
{
size_t hash = 0;
for (auto ch : key)
{
hash *= 131;
hash += ch;
}
return hash;
}
};
struct APHash
{
size_t operator()(const string& key)
{
unsigned int hash = 0;
int i = 0;
for (auto ch : key)
{
if ((i & 1) == 0)
{
hash ^= ((hash << 7) ^ (ch) ^ (hash >> 3));
}
else
{
hash ^= (~((hash << 11) ^ (ch) ^ (hash >> 5)));
}
++i;
}
return hash;
}
};
struct DJBHash
{
size_t operator()(const string& key)
{
unsigned int hash = 5381;
for (auto ch : key)
{
hash += (hash << 5) + ch;
}
return hash;
}
};
接下来我们就要实现这个类,首先这个类肯定需要一个模板,模板中的第一个参数N表示最多要存储数据的个数,第二个参数x表示平均存储一个数据需要开辟多少个比特位,然后就是一个类型参数用来表示记录的数据类型,然后就是三个参数用来表示使用的模板参数,为了方便使用这里可以添加一下模板参数,那么这里的哈希函数模板就是对应的上面的三个哈希函数,根据上面的推断x的值就是4,默认标记的数据就是string,那么布隆过滤器的底层就是 通过位图来实现,所以这里就得将我们之前实现的位图给搬过来,那么这里的代码就如下:
template<size_t n>
class bitset
{
public:
bitset()
{
ch.resize(n / 8 + 1);
}
void set(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
ch[i] |= (1 << j);
}
void reset(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
ch[i] &= ~(1 << j);
}
bool test(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
return ch[i] & (1 << j);
}
private:
vector<char> ch;
};
那么布隆过滤器的大致框架就如下:
template<size_t N,
size_t X=4,
class K=string,
class HashFunc1= BKDRHash,
class HashFunc2= APHash,
class HashFunc3= DJBHash>
class BloomFilter
{
public:
void set(const K& key)
{
}
bool test(const K& key)
{
}
private:
bitset<N* X> _bs;
};
对于set函数这里就可以使用三个哈希函数得到三个位置,然后调用_bs的set函数将这三个位置全部初始化为1即可,那么这里的代码就如下:
void set(const K& key)
{
size_t hash1 = HashFunc1()(key) % (N * X);
size_t hash2 = HashFunc2()(key) % (N * X);
size_t hash3 = HashFunc3()(key) % (N * X);
_bs.set(hash1);
_bs.set(hash2);
_bs.set(hash3);
}
因为只要一个数据对应的三个位置有一个为0,那么这个数据就是不存在的,所以这里就可以先一步一步的得到三个位置的数据,然后再一个一个的判断只要有一个为0那么我们就返回false,如果三个都为1的话我们就返回true,那么这里的代码就如下:
bool test(const K& key)
{
size_t hash1 = HashFunc1()(key) % (N * X);
if (!_bs.test(hash1))
{
return false;
}
size_t hash2 = HashFunc2()(key) % (N * X);
if (!_bs.test(hash2))
{
return false;
}
size_t hash3 = HashFunc3()(key) % (N * X);
if (!_bs.test(hash2))
{
return false;
}
return true;
}
那么实现到这里我们的代码就差不多完成了,大家可能会有疑问为什么布隆过滤器没有删除函数呢?布隆过滤器是不支持reset的,因为当你删除一个值的时候很可能会影响其他值得稳定性,那这里能不能设计另外一个形式的布隆过滤器使得能够支持删除呢?答案是通过计数来实现,当一个值对应的存在数据的时不是讲对应位置上的数据变成1而是加1,删除的时候就是将其值减一,但是这种方法会带来一个其他的问题,之前是通过一个比特位来表示一个数据在还是不在并且还是多个对应的比特位同时判断,如果使用计数的方式来判断的话一个位就不足以记录了,可能要用多个位来进行存储这样就会让空间的消耗成倍的增加,所以布隆过滤器直接没有删除函数,那么看到这里我们的布隆过滤器就完成了完整的代码如下:
template<size_t N,
size_t X=4,
class K=string,
class HashFunc1= BKDRHash,
class HashFunc2= APHash,
class HashFunc3= DJBHash>
class BloomFilter
{
public:
void set(const K& key)
{
size_t hash1 = HashFunc1()(key) % (N * X);
size_t hash2 = HashFunc2()(key) % (N * X);
size_t hash3 = HashFunc3()(key) % (N * X);
_bs.set(hash1);
_bs.set(hash2);
_bs.set(hash3);
}
bool test(const K& key)
{
size_t hash1 = HashFunc1()(key) % (N * X);
if (!_bs.test(hash1))
{
return false;
}
size_t hash2 = HashFunc2()(key) % (N * X);
if (!_bs.test(hash2))
{
return false;
}
size_t hash3 = HashFunc3()(key) % (N * X);
if (!_bs.test(hash3))
{
return false;
}
return true;
}
private:
bitset<N* X> _bs;
};
布隆过滤器的测试
布隆过滤器的代码实现完了,我们这里就可以写一段代码来进行一下测试,首先让布隆过滤器存储一系列不相同的字符串,那么这里的代码就如下:
void test_bloomfilter2()
{
const size_t N = 100000;
BloomFilter<N> bf;
std::vector<std::string> v1;
std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";
for (size_t i = 0; i < N; ++i)
{
v1.push_back(url + std::to_string(i));
}
for (auto& str : v1)
{
bf.set(str);
}
}
然后我们就制造一些与上面相似的字符串来进行测试,判断当前的字符串是否存在,虽然后面的字符串与上面的相似但是他们确实都不存在,所以在测试的时候只要出现了存在就说明当前字符串发生了误报,然后我们就可以创建一个变量用来记录发生误报的字符串的数目,然后除以所有测试字符串的总和就可以了,那么测试的完整代码如下:
void test_bloomfilter2()
{
const size_t N = 100000;
BloomFilter<N> bf;
std::vector<std::string> v1;
std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";
for (size_t i = 0; i < N; ++i)
{
v1.push_back(url + std::to_string(i));
}
for (auto& str : v1)
{
bf.set(str);
}
std::vector<std::string> v2;
for (size_t i = 0; i < N; ++i)
{
std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";
url += std::to_string(999999 + i);
v2.push_back(url);
}
size_t n2 = 0;
for (auto& str : v2)
{
if (bf.test(str))
{
++n2;
}
}
cout << "相似字符串误判率:" << (double)n2 / (double)N << endl;
}
将上面的代码运行一下就会有下面的结果:
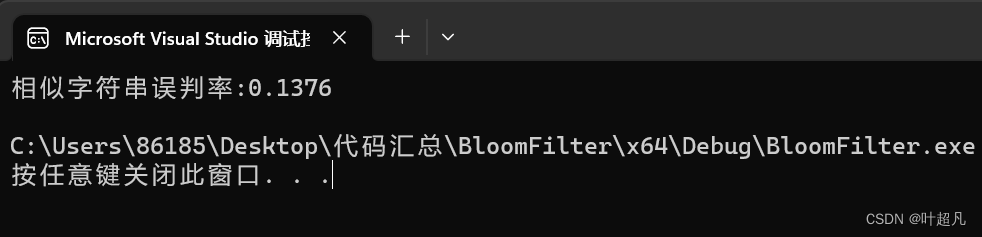
可以看到这里误报的概率为0.2812,使用上面的思路我们还可以测试一下不相似的字符串的误报率又是多少,那么这里的代码就如下:
std::vector<std::string> v3;
for (size_t i = 0; i < N; ++i)
{
string url = "zhihu.com";
url += std::to_string(i + rand());
v3.push_back(url);
}
size_t n3 = 0;
for (auto& str : v3)
{
if (bf.test(str))
{
++n3;
}
}
cout << "不相似字符串误判率:" << (double)n3 / (double)N << endl;
代码的运行结果如下:
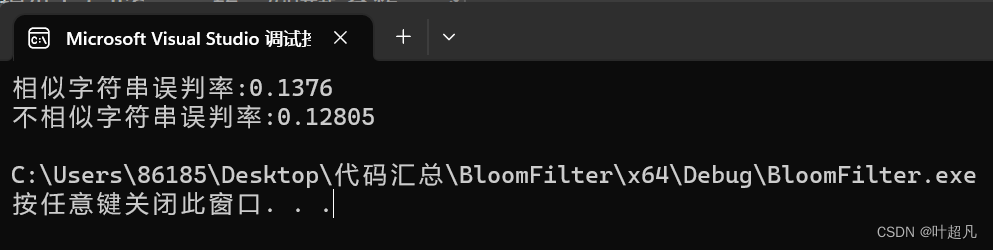
可以看到不相似的字符串的误报率会更低,我们还可以对上面的代码进行修改,原来是插入一个数据要开辟4个空间,那么如果我们开辟6倍的空间误报率会不会降低呢?我们来看看测试的结果:
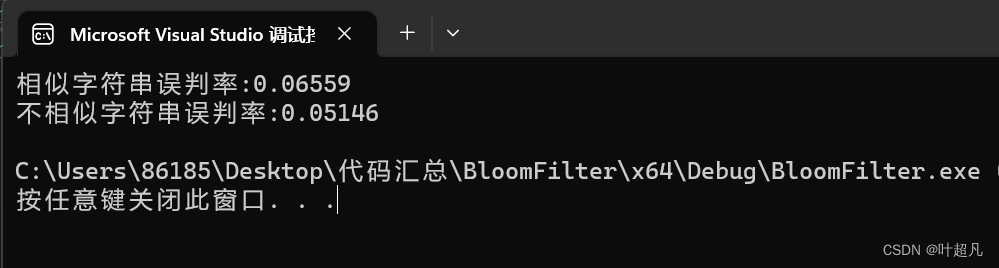
是不是明显的降低了对吧,那这个时候我们再保持当前倍率的不变多添加一个哈希函数呢?他的误报率会进一步降低吗?那这里的哈希函数就如下:
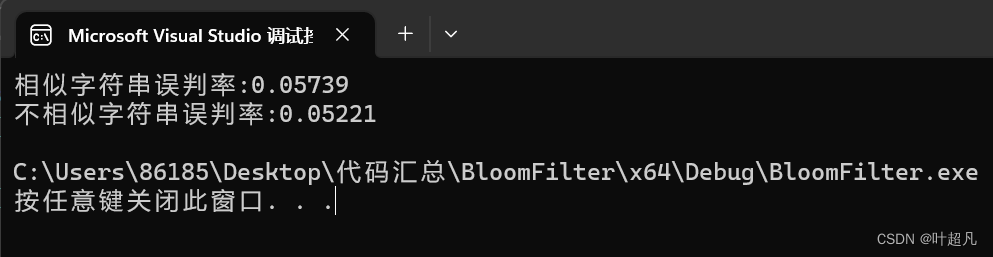
可以看到误报率更进一步的降低,但是这个降低是用更多的额外空间换来的,所以这就是用空间来换取误报率,那么这就是布隆过滤器的测试。






![[MySQL]MySQL表的约束](https://img-blog.csdnimg.cn/img_convert/b9e4b96ebb23d89bbbd83524581e5c43.png)