什么是梯度下降

根据已有数据的分布来预测可能的新数据，这是回归

希望有一条线将数据分割成不同类别，这是分类

无论回归还是分类，我们的目的都是让搭建好的模型尽可能的模拟已有的数据

除了模型的结构，决定模型能否模拟成功的关键是参数

只有几个参数是比较简单的，但是模型的参数经常能够达到成千上万，我们无一一法手动设定，需要机器自己手动去寻找，这个过程就是我们常说的学习或者训练，在训练过程中，我们通常会使用一个工具来帮助模型调整参数，这个工具就是损失函数。

什么是损失函数？

在训练开始之前，模型代表的分布与真实的分布之间会存在一定的差异，我们以一个函数去表示误差，我们以一个函数去表示误差，有时也被称为误差函数。既然损失函数代表的是误差，那么一旦我们找到函数值最小的位置，就等于找到了接近正确的分布。

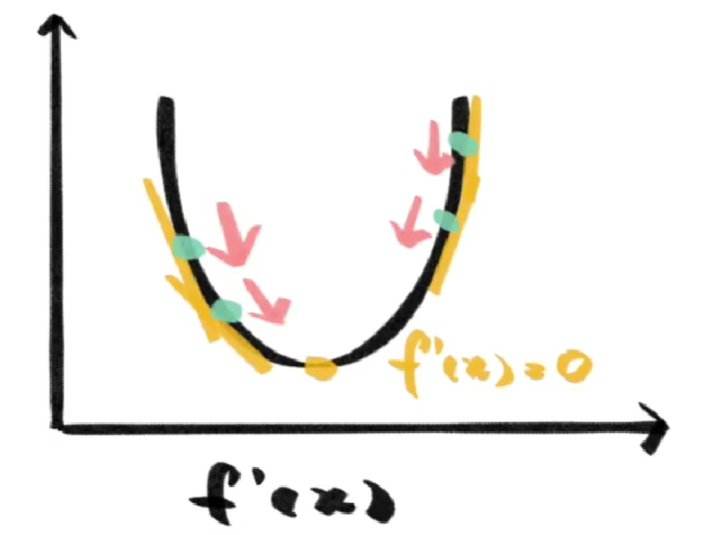
如何去找这个位置，如果我们的函数是一个开口向上的二次函数，导数就是我们最好的向导，导数为0的位置是二次函数的最低点。

无论从哪里开始，只要不断向导数绝对值更低的方向调整，就能找到损失函数的最低点。

真实的损失函数更像崎岖不平的山区，找到最低点没那么容易，这时我们就需要梯度(Gradient)，虽然它也不知道最低点在哪，但可以像导数一样为我们指出向下的方向，顺着它的指引，我们总会来到山下。

至于梯度下降，就是沿着梯度所指出的方向，一步一步向下走，去寻找损失函数最小值的过程，然后我们就找到了接近正确的模型。