- 多类分类

- 多类分类问题仍然是分类问题,所以预测y的可能结果是少量的,而不是无穷多个,且对于多类分类它>2
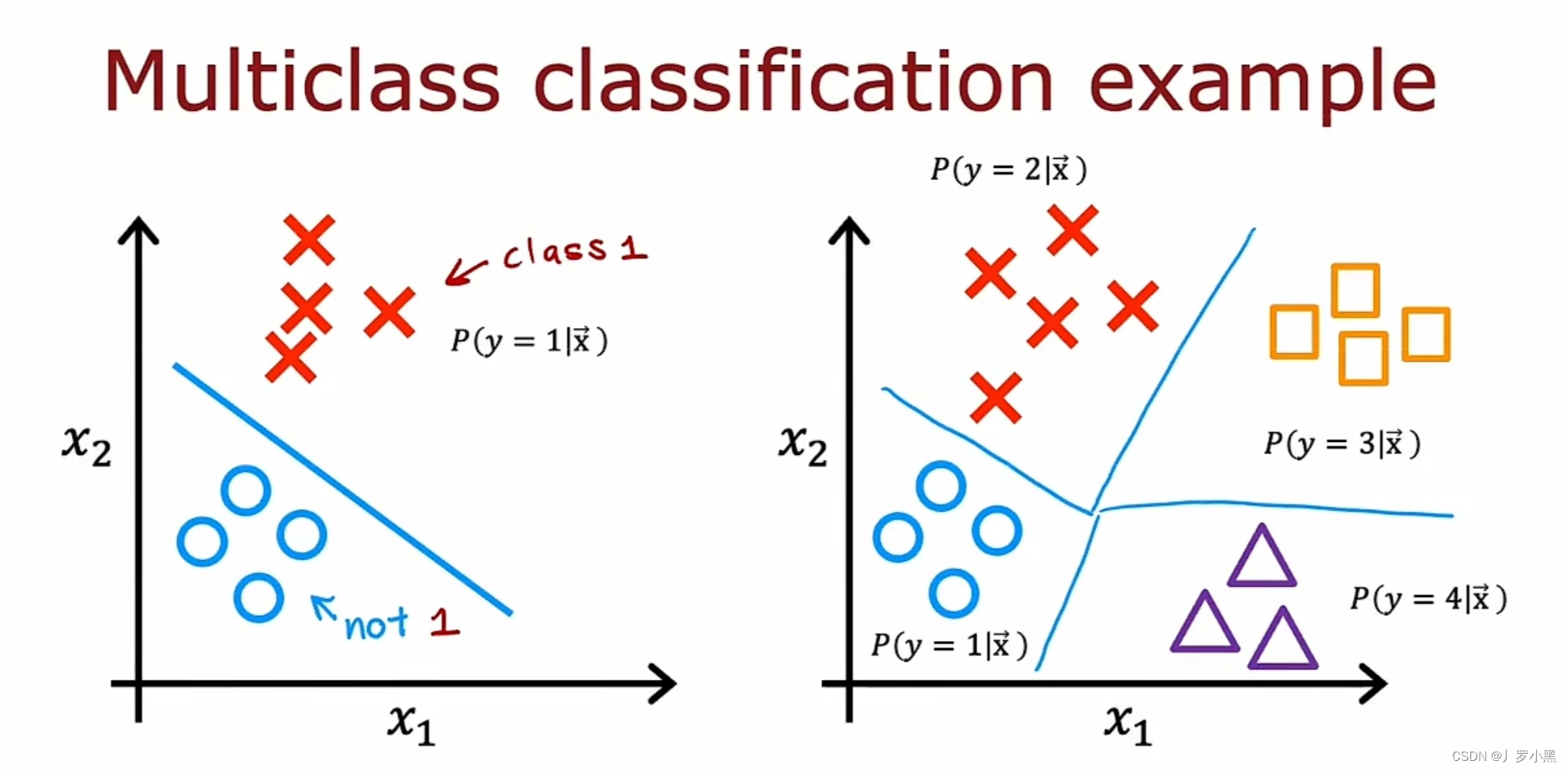
- 如上图:左侧为二分类,右侧为多分类,可以通过决策边界来划分区域
- Softmax回归算法

- 对逻辑回归模型,先计算z,再计算g(z)。此时可以将逻辑回归视为计算两个数字,a₁是当给定x时,预测y取1的概率;a₂则是当给定x时,预测y取0的概率。因为逻辑回归只有两个结果(0、1),所以a₁ + a₂必须为1
- 推广到softmax回归模型,w和b为y取每种结果时的模型参数,先计算z。若此时y有四个结果(1、2、3、4),则可以用softmax回归公式得出a₁、a₂、a₃、a₄,分别为当给定输入特征x,预测y取1、2、3、4的概率,因为该softmax回归模型只有四个结果(1、2、3、4),所以a₁ + a₂ + a₃ + a₄必须为1
- 对于一般情况下的softmax回归模型,先计算z,若此时y有N个结果,则可以用softmax回归公式得出当预测y取j时的概率aj,因为softmax回归模型共有N个结果,所以a₁ + a₂ +… + an必须为1。
- 若N取2,则softmax回归模型的计算结果与逻辑回归模型的计算结果相同。因此softmax回归模型是逻辑回归模型的推广
- Softmax回归算法的损失函数
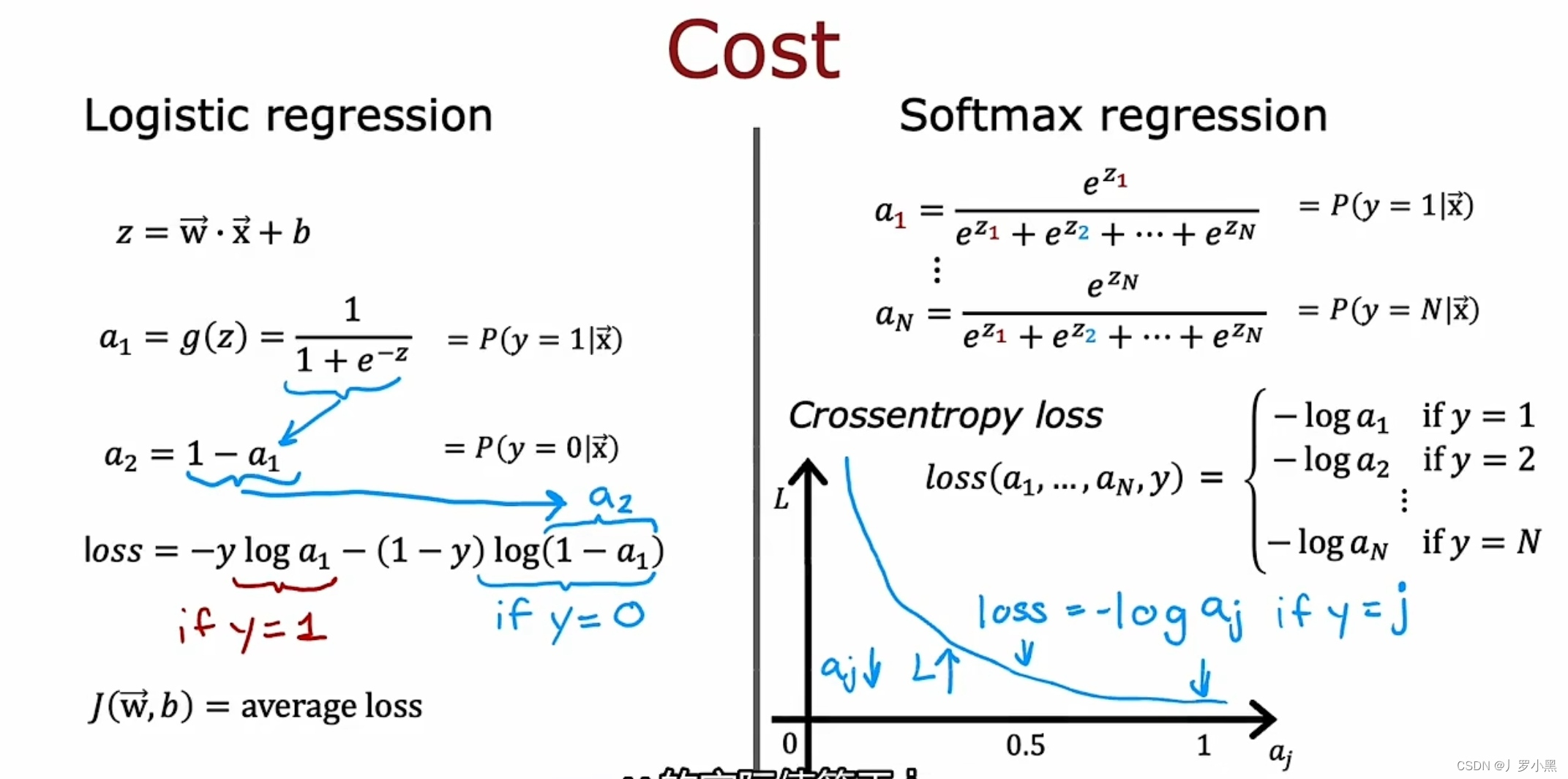
- 对于逻辑回归模型,我们可以用a₂来表示1-a₁。cost function是定义在整个训练集上的,loss function是定义在单个样本上的,且cost function是所有样本的loss function的平均值
- 对于softmax回归模型,在每个训练实例中,y每次只有一个结果,所以每次只能取一个值。但可以用上图的公式来计算对于每个y的损失函数的值
- 由于0<aj<1,所以softmax的损失函数的取值范围为(0,+∞),且当aj越接近1,损失函数的值就越接近0