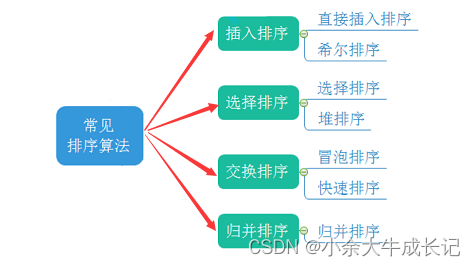
---

1.3常见的七大排序

后面的排序博客也是围绕下面这些排序来讲解的哦，对排序感兴趣的可以关注下喔！！！

---

---

2.直接插入排序

从1.3的图中我们也可以发现插入排序有两种类型—【直接插入排序】、【希尔排序】

它们都属于插入排序，希尔排序是直接插入排序的优化形式。

直接插入排序是一种简单的插入排序法，其基本思想是：

把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为 止，得到一个新的有序序列 。

---

2.3动图助解

---

2.4直接插入排序源码

void InsertSort(int* a, int n)
{
	for (int i = 0; i < n - 1; ++i)
	{
		// [0,end]有序，把end+1位置的值插入，保持有序
		int end = i;
		int tmp = a[end + 1];//插入的值和前面[0,end]的值进行比较
		while (end >= 0)
		{
			if (tmp < a[end])//插入的值小，就往前挪一下
			{
				a[end + 1] = a[end];
				--end;
			}
			else//到这里就是数组中的值<插入的值 || 整个[0,end]的值都>插入的值
			{
				break;
			}
		}
		a[end + 1] = tmp;//放入插入值
	}
}

---

2.5直接插入排序的特性总结

---

---

3.希尔排序( 缩小增量排序 )

【希尔排序】是对上面【直接插入排序】的最坏情况进行优化。

3.1希尔排序概念及思想

希尔排序法又称缩小增量法。

希尔排序法的基本思想是： 先选定一个整数，把待排序文件中所有记录分成个组，所有距离为的记录分在同一组内，并对每一组内的记录进行排序。然后，取，重复上述分组和排序的工作。当到达=1时，所有记录在统一组内排好序。

---

3.2希尔排序图解

【希尔排序】And【直接插入排序】单趟排序的区别

3.3希尔排序源码

void ShellSort(int* a, int n)
{
    //方法一：双层循环（不太推荐）
	/*int gap = 3;*/

	/*for (int j = 0; j < gap; ++j)
	{
		for (int i = j; i < n - gap; i += gap)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}*/
///

    //方法二：单层for循环（推荐）
	// gap > 1时是预排序
	// gap 最后一次等于1，是直接插入排序

	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;//保证最后一次gap=1，就是【直接插入排序】了。

		for (int i = 0; i < n - gap; ++i)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

3.4希尔排序的两种预排序图解

方法一【双层for循环控制】

这种排序将这个数组分成3组数

（红色）——9 6 4 1

（蓝色）——8 5 3

（紫色）——7 5 2

排序的顺序是先排序完红色的4个数，再排序蓝色的3个数，最后排序紫色的3个数 

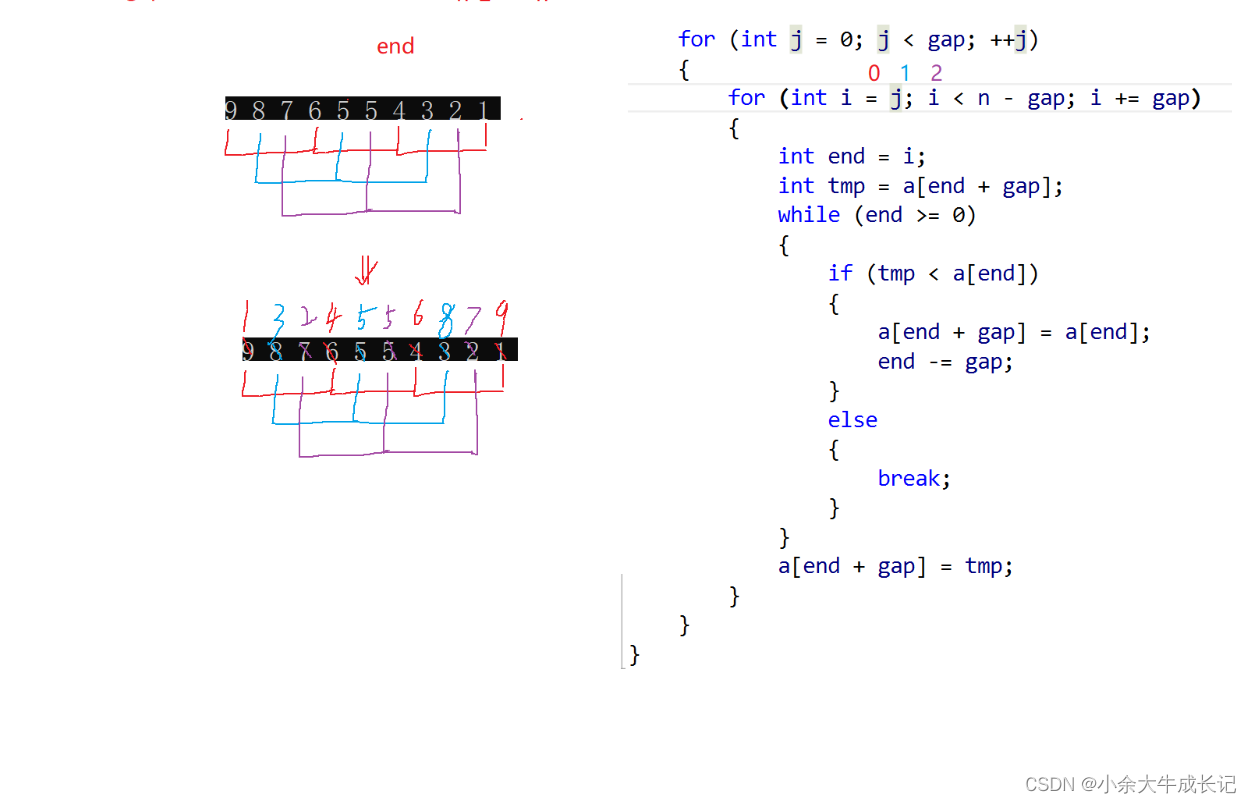
 方法二【单层for循环控制】

这个方法下，就是排序完红色的第1个数，再排序完蓝色的第1个数，最后排序紫色的第1个数—在轮到红色的第2个数.........

---

3.5希尔排序的特性总结

1. 希尔排序是对直接插入排序的优化。

2. 当 gap > 1 时都是预排序，目的是让数组更接近于有序。当 gap == 1 时，数组已经接近有序的了，这样就 会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。

3. 希尔排序的时间复杂度不好计算，因为 gap 的取值方法很多，导致很难去计算，因此在好些树中给出的。                                          

4.希尔排序的时间复杂度都不固定：这边给个大概的平均时间复杂度—O(N^1.3)