提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、使用数值微分计算导数

假设函数是y = x ** 2，如何使用数值微分来计算y 在x = 3时的导师呢？

利用导数的定义

因为h不可能无限接近与0，所以取h = 0.0001

代码如下：

def numerical_diff(f,x):
    h = 1e-4
    return (f(x+h) - f(x-h)) / (2 * h)

def func(x):
    return np.sum(x**2)

运行结果很接近6。
如果输入的x是一维向量，不是一个值的话，代码如下

def numerical_gradient(f,x):
    h = 1e-4
    grad = np.zeros_like(x)
    for i in range(0,x.size):
        ##计算f(x+h)
        temp = x[i]
        x[i] = temp + h
        f_x_h1 = f(x)
        ##计算f(x-h)
        x[i] = temp - h
        f_x_h2 = f(x)

        grad[i] = (f_x_h1 - f_x_h2) / (2*h)
        x[i] = temp
    return grad
def gradient_desent(f,x,lr = 1e-1,step_num = 100):
    for i in range(100):
        grad = numerical_gradient(f,x)
        x = x - lr * grad
    return x    
print(gradient_desent(func,np.array([-3.0,4.0])))    

按照梯度下降的方法迭代100次，得到结果为

说明很接近0，已经收敛到了极小值。

如果说输入是一个多维度的数据，对应的数值微分代码还要更改。

二、计算图

针对这样一个问题，构建的计算图如下

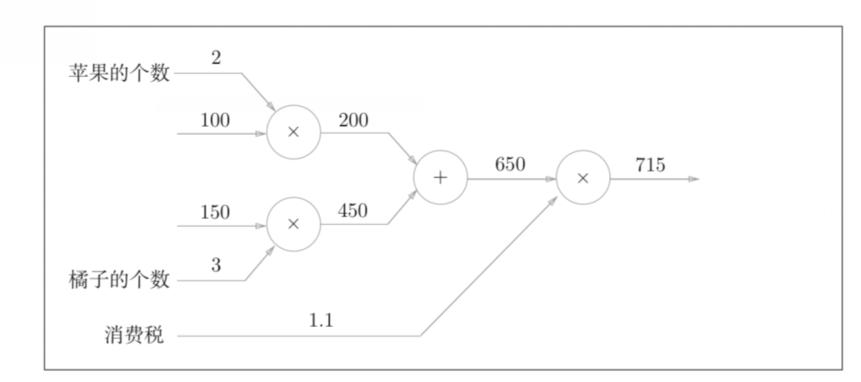
该图中，只有正向传播（从左到右的计算过程），还没有反向传播的值。
计算图中只有加法和乘法两种节点。

使用计算图的优点如下
（1）无论全局是多么复杂的计算，都可以简化问题，然后计算简单的问题。
（2）利用计算图可以将中间的计算结果全部保存起来。
（3）可以通过反向传播高效的计算导数。

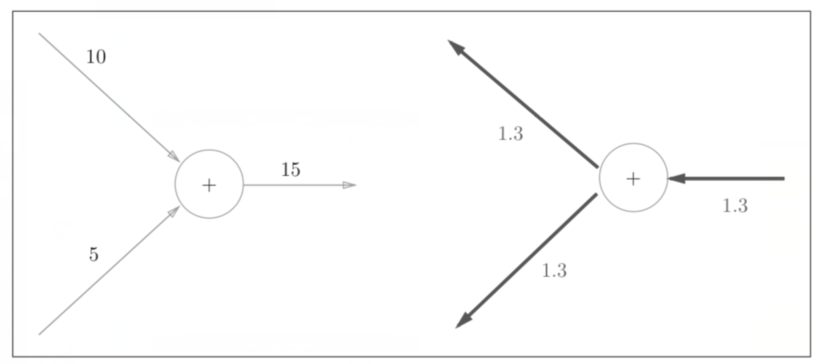
反向传播时，加法节点和乘法节点的反向传播如下
加法节点

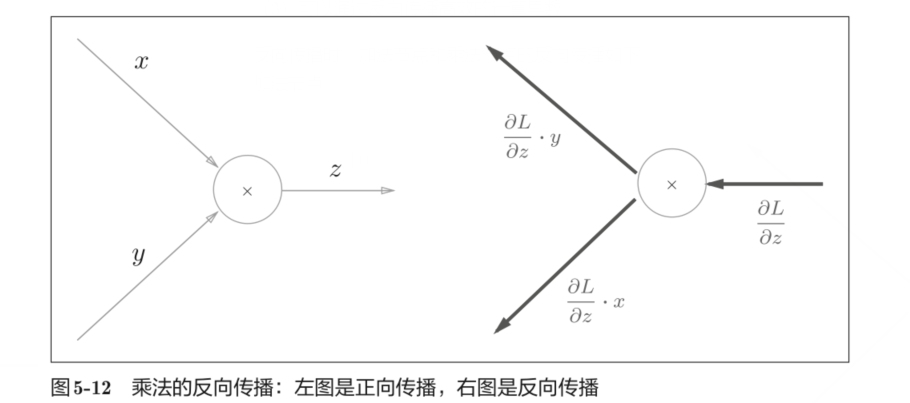
乘法节点

在上面的例子中，加入反向传播之后的完整计算图如下

代码实现如下
乘法层

class MulLayer:
    def __init__(self):
        self.x = None
        self.y = None
        
    def forward(self,x,y):
        self.x = x
        self.y = y
        out = x * y
        
    def backword(self,dout):
        dx = dout * self.y
        dy = dout * self.x
        
        return dx,dy

加法层

class AddLayer:
    def __init__(self):
        self.x = None
        self.y = None

    def forward(self,x,y):
        self.x = x
        self.y = y
        out = x + y

    def backword(self,dout):
        dx = dout
        dy = dout

        return dx,dy

除此之外，包括relu，sigmoid，softmax层都应该包含前向传播和反向传播两个方法。

---