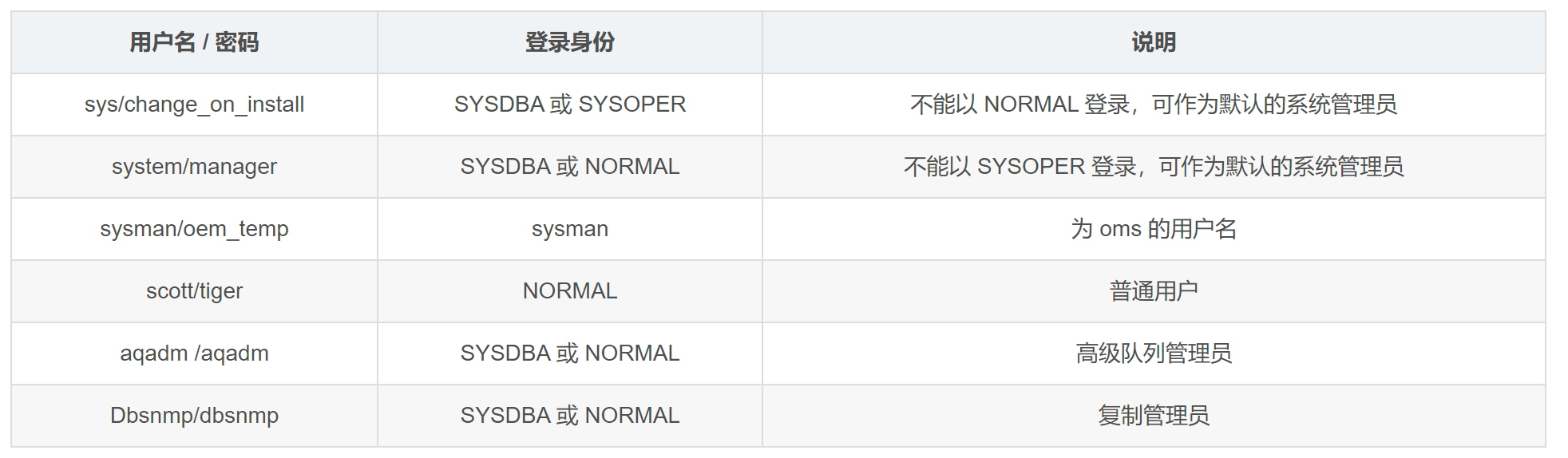
李瀚荪版电分第二版

-----------------------------------------------------------------------------------------------------------------------------

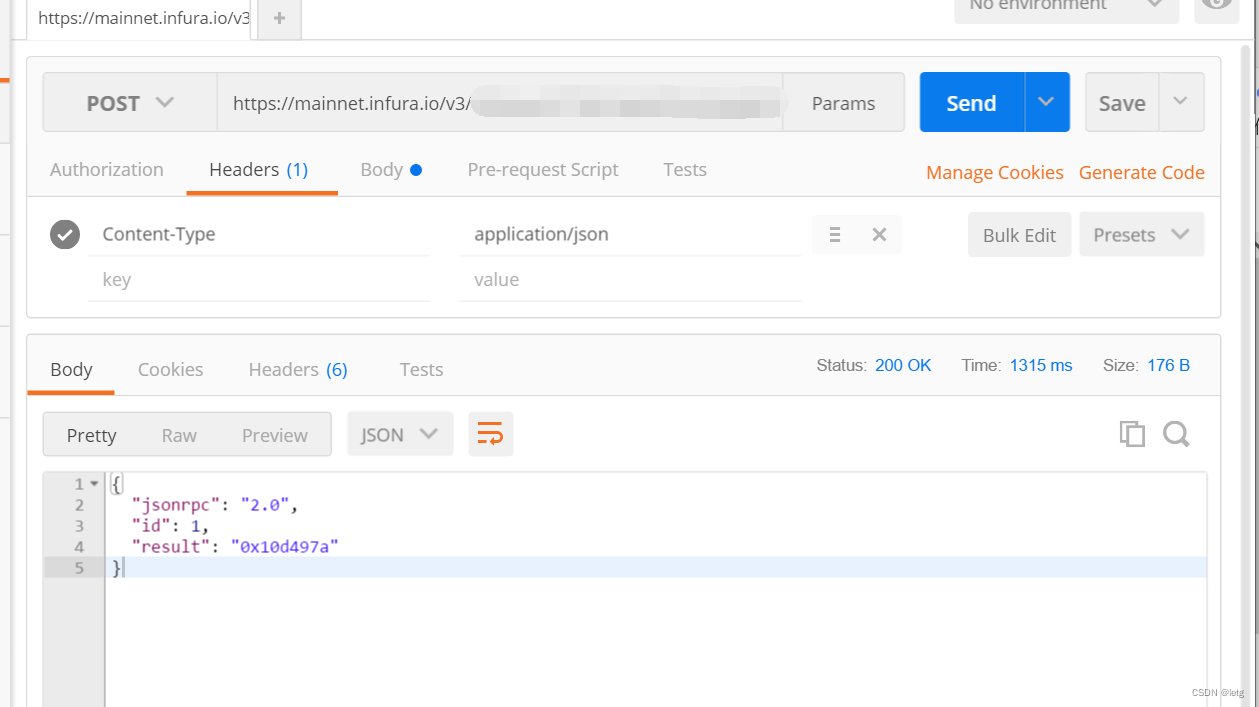
求单口网络的VCR

两大基本方法：

1.外接电流源求电压；

2.外接电压源求电流；

-----------------------------------------------------------------------------------------------------------------------------

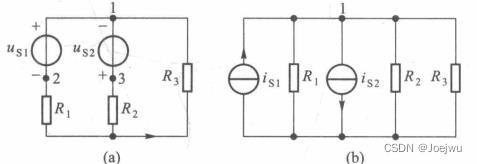
常用等效规律

电压源串联电阻与电流源并流电阻的等效替换

需要注意的是此时电压源与电流源的方向问题，示例如下；

即替换之后电压源电压升的方向与电流源电流流出的方向一致；

 

-----------------------------------------------------------------------------------------------------------------------------

戴维南定理

戴维南定理（Thevenin's Theorem）是电路理论中的重要定理，它提供了简化复杂电路分析的方法。根据戴维南定理，任何线性电路都可以用一个等效的电压源和串联的等效电阻来表示。

具体来说，根据戴维南定理，一个线性电路可以用以下等效电路表示：

1. 等效电压源（Thevenin Voltage Source）：将原始电路的所有电源和电压源替换为一个单一的电压源，其电压等于原始电路在两个端点之间的开路电压（无负载时的电压）。

2. 等效电阻（Thevenin Resistance）：将原始电路在两个端点之间移除所有电源和电压源，然后通过这两个端点测量电阻。这个电阻被视为等效电路的输出电阻。

等效电压源和等效电阻组成了戴维南等效电路，它能够提供与原始电路相同的电压和电流响应，当连接到外部负载时可以模拟原始电路的行为。

使用戴维南定理的步骤如下：

1. 找到要简化的电路的关键节点，即在哪个位置需要求解电压或电流。

2. 将其他部分的电源和电压源从电路中移除，取下两个关键节点之间的电路部分。

3. 计算两个关键节点之间的开路电压，即在没有连接任何负载的情况下，测量两个节点之间的电压。

4. 计算两个关键节点之间的电阻，即在没有连接任何电源和电压源的情况下，测量两个节点之间的电阻。

5. 将等效电压源和等效电阻连接到原始电路的关键节点处。

-----------------------------------------------------------------------------------------------------------------------------

诺顿定理

诺顿定理（Norton's Theorem）是电路理论中的另一个重要定理，与戴维南定理相对应。根据诺顿定理，任何线性电路都可以用一个等效的电流源和并联的等效电阻来表示。

具体来说，根据诺顿定理，一个线性电路可以用以下等效电路表示：

1. 等效电流源（Norton Current Source）：将原始电路的所有电源和电流源替换为一个单一的电流源，其电流等于原始电路在两个端点之间的短路电流（无负载时的电流）。

2. 等效电阻（Norton Resistance）：将原始电路在两个端点之间移除所有电源和电流源，然后通过这两个端点测量电阻。这个电阻被视为等效电路的输入电阻。

等效电流源和等效电阻组成了诺顿等效电路，它能够提供与原始电路相同的电压和电流响应，当连接到外部负载时可以模拟原始电路的行为。

使用诺顿定理的步骤如下：

1. 找到要简化的电路的关键节点，即在哪个位置需要求解电压或电流。

2. 将其他部分的电源和电流源从电路中移除，取下两个关键节点之间的电路部分。

3. 计算两个关键节点之间的短路电流，即在将两个节点短路连接的情况下，测量通过这个短路的电流。

4. 计算两个关键节点之间的电阻，即在没有连接任何电源和电流源的情况下，测量两个节点之间的电阻。

5. 将等效电流源和等效电阻连接到原始电路的关键节点处。

通过诺顿定理，可将复杂的电路简化为一个更简单的等效电路，从而方便进行分析和计算。诺顿定理和戴维南定理可以相互转换，因为是等效的。

-----------------------------------------------------------------------------------------------------------------------------

诺顿定理和戴维南定理应该如何选择，或者说对应不同的电路，选择哪一种等效电路更简单？

在选择诺顿定理或戴维南定理时，可以根据具体情况和需要考虑以下因素：

1. 电路结构：诺顿定理和戴维南定理在等效电路的构建方式上有所不同。对于某些电路结构，其中一个定理可能更适用或更容易使用。例如，当电路包含大量并联元件时，诺顿定理可能更容易应用，因为它使用并联等效电阻来简化电路。

2. 求解目标：如果你需要求解电路中的电压分布或电流分布，那么戴维南定理可能更适合。如果你更关注电路中的电流源和负载之间的关系，那么诺顿定理可能更合适。

3. 电路参数：有时，根据电路的具体参数，其中一个定理可能提供更简单的等效电路。你可以根据电路的特点和参数来决定使用哪个定理。

4. 个人偏好和经验：选择定理的另一个因素是个人的偏好和经验。你可能更熟悉其中一个定理，或者在过去的实践中发现其中一个定理更适合你的工作流程。

需要注意的是，诺顿定理和戴维南定理是等效的，它们提供了相同的信息，只是以不同的形式呈现。因此，可以根据具体情况选择更简单或更方便的方法。在实际应用中，根据电路的特点和求解需求，选择适合的定理将有助于简化分析和计算的过程。

书中的说法较为简单，即求短路电流简单的电路就用诺顿定理，求开路电压简单的电路就用戴维南定理；

-----------------------------------------------------------------------------------------------------------------------------

双口网络

根据自变量的选择情况，分为六种双口网络的VCR；

混合型VCR适用于低频晶体管电路，对晶体管来说h参数最易求出；

传属型VCR适用于信号或电力传输上；

四种双口网络的参数：

-----------------------------------------------------------------------------------------------------------------------------

分析含理想二极管的电路

首先需要确定的是该二极管是否导通，可通过戴维南定理来解决；

对理想二极管来说，导通时其电阻可视为0，截止时，电阻可视为无穷大；

简单来说，就是先把含有二极管的支路隔离出来，然后计算得到其他部分电路戴维南等效电路，然后再把二极管放进等效电路中，据此来判断此时的二极管是否导通；

-----------------------------------------------------------------------------------------------------------------------------