傅里叶变换可以简单理解为用一系列三角函数去拟合一个目标函数。为什么可以用三角函数拟合？因为三角函数 是一组正交基。

先来回顾一下正交的概念，在二维平面坐标系中，与这两个单位向量，正交（内积为0，相互垂直），平面坐标系内任意一个向量，都可以用这两个单位向量来表示，就是在平面坐标系内的坐标。

在三维空间中，这三个向量两两相互正交（内积为0，相互垂直），同理，三维空间坐标系内任何一个向量都可以看作是这三个单位向量的线性组合。这三个向量就是三维空间坐标系内的正交基。

不仅向量可以作为正交基，函数同样可以作为正交基。若函数在区间上存在如下性质：

则称函数在区间上正交。三角函数中在区间内，任意两个都正交，因此三角函数是一组正交基。待拟合目标函数就可以三角函数正交基的线性组合。

 就是函数在三角函数正交基这个坐标系内的坐标。傅里叶变换就是求一个函数在三角函数正交基坐标系的坐标，也可以理解为用一系列三角函数去拟合这个函数，我们要求的就是拟合过程中的系数：

import numpy as np
from scipy.fftpack import fft
import matplotlib.pyplot as plt


def FFT(Fs, data):
    """
    对输入信号进行FFT
    :param Fs:  采样频率
    :param data:待FFT的序列
    :return:
    """
    L = len(data)  # 信号长度
    N = np.power(2, np.ceil(np.log2(L)))  # 下一个最近二次幂，也即N个点的FFT
    result = np.abs(fft(x=data, n=int(N))) / L * 2  # N点FFT
    axisFreq = np.arange(int(N / 2)) * Fs / N  # 频率坐标
    result = result[range(int(N / 2))]  # 因为图形对称，所以取一半
    return axisFreq, result


if __name__ == '__main__':
    Fs = 10000  # 采样频率
    f1 = 100  # 信号频率1
    f2 = 2000  # 信号频率2
    t = np.linspace(0, 1, Fs)  # 生成 1s 的时间序列
    # 给定信号
    y = 2 * np.sin(2 * np.pi * f1 * t) + 5 * np.sin(2 * np.pi * f2 * t)
    # 第一步，对没有添加噪声的信号进行FFT，验证分析是否正确
    x, result = FFT(Fs, y)

    # 绘图
    fig1 = plt.figure(figsize=(16, 9))
    plt.title('original data')
    plt.plot(t, y)
    plt.xlabel('time/s')
    plt.ylabel('Amplitude')
    plt.grid()

    fig2 = plt.figure(figsize=(16, 9))
    plt.title('FFT')
    plt.plot(x, result)
    plt.xlabel('Frequency/Hz')
    plt.ylabel('Amplitude')
    plt.grid()
    plt.show()

运行上述python代码，可以看到

 

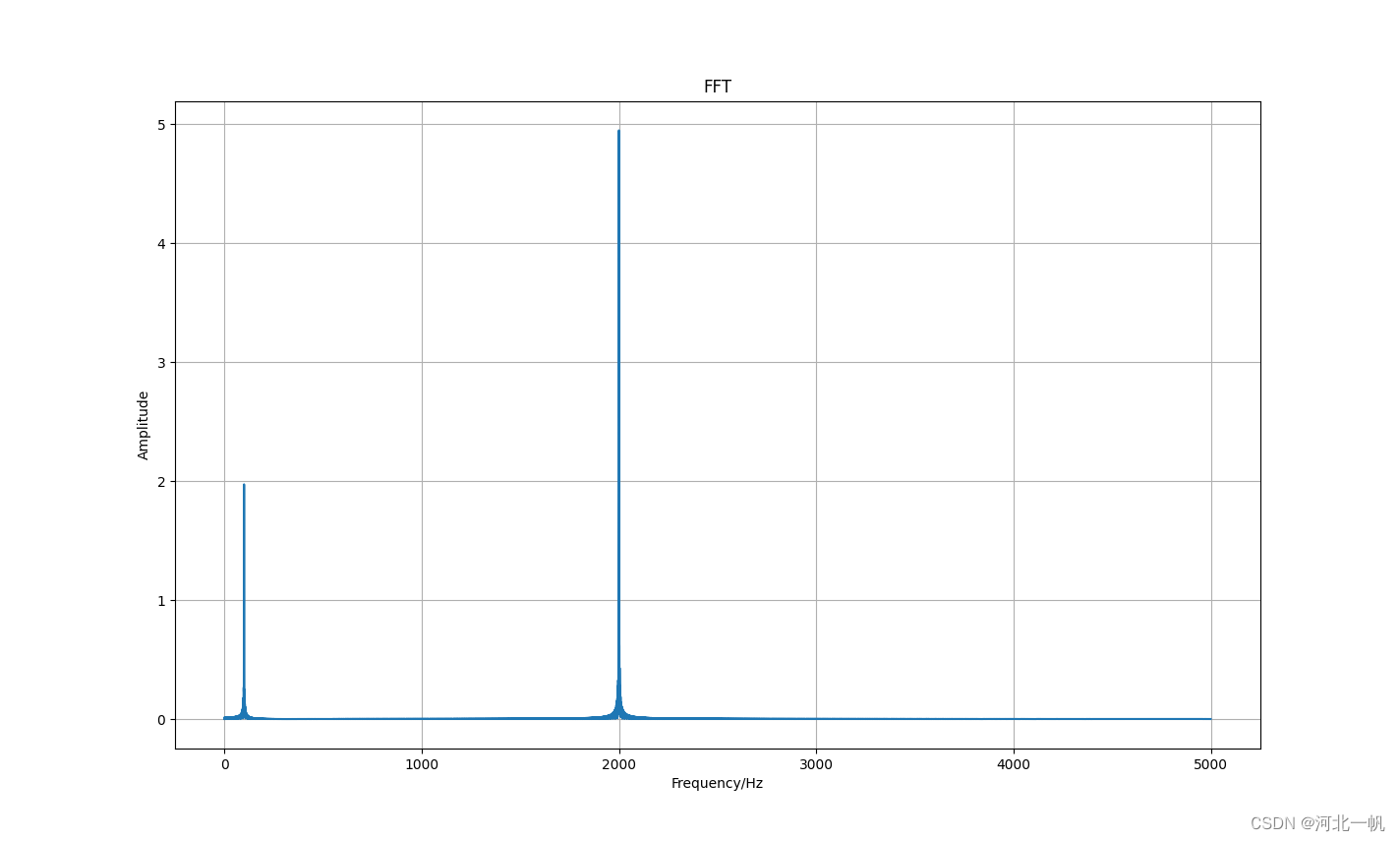
频率为100和频率为2000对应的幅值约为2和5，即待拟合函数中，主要成分就是频率100和2000的基函数，这两个基函数系数分别为2和5。与我们待拟合函数y相一致。