题目

t(t<=500)组case，

给定一个数n(n<=500)，构造一个长为n的数组

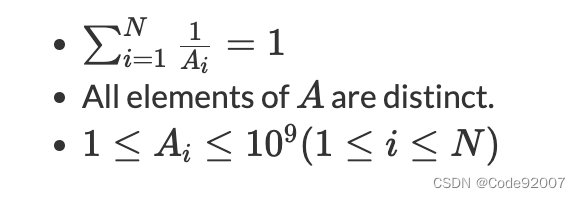
思路来源

官方题解

题解

注意到

...

右边累加，等于1-最后一项，可以把最后一项挪到左边

所以，

1. 当n没有在前面的序列里出现过时，可以用(2,6,12,...,n)来构造一组解

2. 当出现过时，例如当n=6时，序列为(2,6,12,20,30,6)不能满足条件

此时，我们先构造(2,6,12,20,5)，五个数，

然后将每个数乘以2，再将2放回来

即得到(2,4,12,24,40,10)，满足题意

①n冲突的时候，n-1一定不会冲突，因为前面的序列是i*(i+1)的格式，不存在两个相邻的数

②n个数倒数求和=1，每个数乘以2后倒数求和=1/2，再加上1/2即为1，

由于一开始没有1，所以也不会冲突

代码1

#include<iostream>
#include<vector>
#include<algorithm>
#include<set>
#include<map>
#include<queue>
using namespace std;
typedef long long ll;
const int N=5e5+10,up=1e9;
int t,n;
void sol(){
    scanf("%d",&n);
    if(n==2){
        puts("No");
        return;
    }
    if(n==1){
        puts("Yes\n1");
        return;
    }
    vector<int>ans;
    bool no=0;
    for(int i=1;i<n;++i){
        ans.push_back(i*(i+1));
        no|=(i*(i+1)==n);
    }
    if(no){
        ans.pop_back();
        ans.push_back(n-1);
        for(auto &v:ans)v*=2;
        ans.push_back(2);
    }
    else{
        ans.push_back(n);
    }
    puts("Yes");
    for(auto &v:ans)printf("%d ",v);
    puts("");
}
int main(){
    scanf("%d",&t);
    while(t--){
        sol();
    }
    return 0;
}

代码2（我的乱搞）

也是基于这个等式，用最大的数一拆二扩展，直至满足n个数，

[1,1e9]值域很宽，冲撞的可能性很小很小

#include<iostream>
#include<vector>
#include<algorithm>
#include<set>
#include<map>
#include<queue>
using namespace std;
typedef long long ll;
const int N=5e5+10,up=1e9;
int t,n;
void sol(){
    scanf("%d",&n);
    if(n==2){
        puts("No");
        return;
    }
    if(n==1){
        puts("Yes\n1");
        return;
    }
    priority_queue<int>q;
    map<int,int>now;
    int c=3;
    for(auto &v:{2,3,6}){
        q.push(v);
        now[v]=1;
    }
    while(c<n){
        int x=q.top();q.pop();
        if(1ll*x*(x+1)<=up){
            int v=x*(x+1);
            if(!now[x+1] && !now[v]){
                now[x]--;
                now[x+1]++;now[v]++;
                q.push(x+1);q.push(v);
                c++;
            }
        }
    }
    puts("Yes");
    for(auto &v:now){
        if(v.second)printf("%d ",v.first);
    }
    puts("");
}
int main(){
    scanf("%d",&t);
    while(t--){
        sol();
    }
    return 0;
}