1. 提出问题

问题：有一组训练数据集
$T=\{(x_1,y_1),(x_2,y_2),\dots ,(x_N,y_N)\}$
其中$x_i\in \mathcal{X}=R^n$， y i ∈ Y = { + 1 , − 1 } y_i\in\mathcal{Y}=\{+1,-1\} yi​∈Y={+1,−1}，$i=1,2,\dots ,N$，求一个超平面 $S$ 使其能够完全将$y_i=+1$ 和 $y_i=-1$ 的点分开。

2. 感知机及其损失函数

一个线性平面的方程为$y=w\cdot x+b$，要将$y_i=+1$ 和 $y_i=-1$ 的点分开则需要让求解方程的的因变量为$\pm 1$，所以需要一个sign函数，sign函数的表达式为：

$sign(x)=\{\begin{array}{l}+1\\ -1\end{array}\dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots (2.1)$

所以求解方程为：

$f(x)=sign(w\cdot x+b)\dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots (2.2)$

这个求解方程即被称为感知机。要求解这个方程只需要确定$w$ 和 $b$ 的值，为了确定参数值，就需要定义一个损失函数并将损失函数及小化。

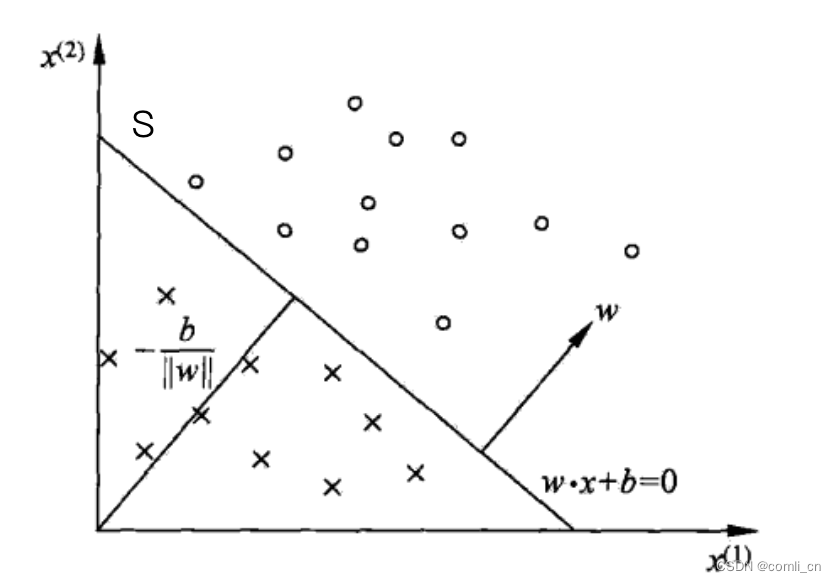
感知机所用的损失函数为误分类点到超平面 $S$ 的总距离。首先写出空间 $R^n$ 中任意一点 $x_0$ 到超平面 $S$ 的距离：

$\frac{1}{||w||}|w\cdot x_0+b|\dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots (2.3)$

这里 $||w||$ 是 $w$ 的 $L_2$ 范数。

对于误分类的数据 $(x_i,y_i)$ 来说，$-y_i(w_i\cdot x_i+b)>0$ 成立。因为当 $w\cdot x_i+b>0$ 时，$y_i=-1$，而当 $w\cdot x_i+b<0$ 时，$y_i=+1$ ，因此，误分类点 $x_i$ 到超平面 $S$ 的距离是：

$-\frac{1}{||w||}{y}_i(w\cdot x_i+b)\dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots (2.4)$

这样，假设超平面 $S$ 的误分类点集合为 $M$ ，那么所有误分类点到超平面 $S$ 的总距离为：

$-\frac{1}{||w||}{\sum }_{x_i\in M}{y}_i(w\cdot x_i+b)\dots \dots \dots \dots \dots \dots \dots \dots \dots \dots (2.5)$

不考虑$\frac{1}{||w||}$ ，就得到感知机学习的损失函数。

给定训练数据集 $T=(x_1,y_1),(x_2,y_2),\dots ,(x_N,y_N)$，其中，$x_i\in \mathcal{X}=R^n$， y i ∈ Y = { + 1 , − 1 } y_i\in \mathcal{Y}=\{+1, -1\} yi​∈Y={+1,−1}，$i=1,2,\dots ,N$ . 感知机$sign(w\cdot x+b)$ 学习的损失函数定义为：

$L(w,b)=-{\sum }_{x_i\in M}{y}_i(w\cdot x_i+b)\dots \dots \dots \dots \dots \dots \dots \dots (2.6)$

其中 $M$ 为误分类点的集合，这个损失函数就是感知机学习的经验风险函数。

3. 求解

给定训练数据集 $T=(x_1,y_1),(x_2,y_2),\dots ,(x_N,y_N)$，其中，$x_i\in \mathcal{X}=R^n$， y i ∈ Y = { + 1 , − 1 } y_i\in \mathcal{Y}=\{+1, -1\} yi​∈Y={+1,−1}，$i=1,2,\dots ,N$ ，求参数 $w,b$ ，使其为以下损失函数极小化问题的解：

$mi{n}_{w.b}L(w,b)=-{\sum }_{x_i\in M}{y}_i(w\cdot x_i+b)\dots \dots \dots \dots \dots (3.1)$

其中 $M$ 为误分类点的集合。

采用随机梯度下降法来求解。首先，任意选取一个超平面 $w_0,b_0$，然后用随机梯度下降法不断地极小化目标函数，极小化的过程中不是一次使 $M$ 中所有误分类点的梯度下降，而是一次随机选取一个误分类点使其梯度下降。

假设误分类点集合 $M$ 是固定的，那么损失函数 $L(w,b)$ 的梯度由：

${\nabla }_{w}L(w,b)=-{\sum }_{x_i\in M}{y}_i{x}_i$

${\nabla }_{b}L(w,b)=-{\sum }_{x_i\in M}{y}_i$

给出.

随机选取一个误分类点$(x_i,y_i)$ ，对$w,b$ 进行更新：

$w\leftarrow w+\eta y_i{x}_i\dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots (3.2)$

$b\leftarrow b+\eta y_i\dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots (3.3)$

式中$\eta (0<\eta \le 1)$ 是步长，在统计学系中又称为学习率. 这样，通过迭代可以期待损失函数 $L(w,b)$ 不断减小，直到为0.

4. 例子

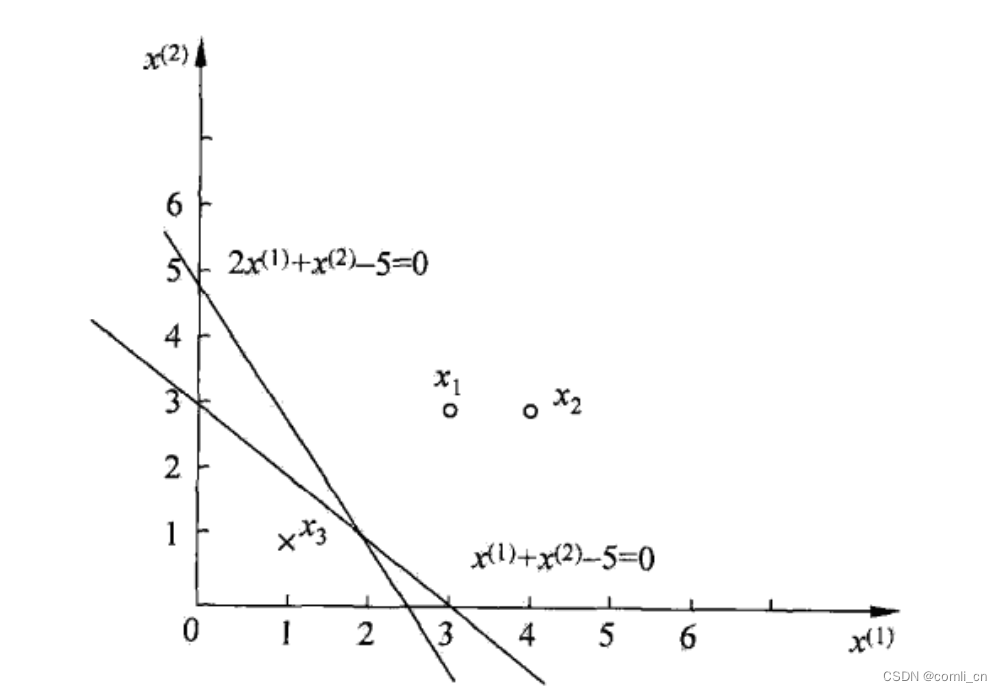
如下图所示的训练数据集，其正实例点是 $x_1=(3,3{)}^T$，$x_2=(4,3{)}^T$，负实例点是 $x_3=(1,1{)}^T$，试用感知机学习算法的原始形式求感知机模型 $f(x)=sign(w\cdot x+b)$. 这里 $w=(w^{(1)},w^{(2)}{)}^T$，$x=(x^{(1)},x^{(2)}{)}^T$.

解：

最优化问题为：

$mi{n}_{w.b}L(w,b)=-{\sum }_{x_i\in M}{y}_i(w\cdot x_i+b)$

用第3节的方式求解 $w,b$，设学习率 $\eta =1$.

（1）取初值 $w_0=0,b_0=0$
（2）对$x_1=(3,3{)}^T$，$y_1(w_0\cdot x_1+b_0)=0$，未能=被正确分类，更新 $w,b$

$w_1=w_0+y_1{x}_1=(3,3{)}^T,b_1=b_0+y_1=1$

得到线性模型

$w_1\cdot x+b_1=3x^{(1)}+3x^{(2)}+1$

（3）对$x_1,x_2$，显然，$y_1(w_1\cdot x_1+b_1)>0$，被正确分类，不修改$w,b$；
对 $x_3=(1,1{)}^T，y_3(w_1\cdot x_3+b_1)<0$，被误分类，更新 $w,b$.

$w_2=w_1+y_3{x}_3=(2,2{)}^T,b_2=b_1+y_3=0$

得到线性模型

$w_2\cdot x+b_2=2x^{(1)}+2x^{(2)}$

如此继续下去，直到

$w_7=(1,1{)}^T,b_7=-3$

$w_7\cdot x+b_7=x^{(1)}+x^{(2)}-3$

对所有数据点 $y_i(w_7\cdot x_i+b_7)>0$，没有误分类点，损失函数达到极小

分离超平面为：

$x^{(1)}+x^{(2)}-3=0$

感知机模型为：

$f(x)=sign(x^{(1)}+x^{(2)}-3)$