📭从这里开始，我们要开始学习动态规划辣。之后的动态规划有关的文章都是按照这个逻辑来写，首先来介绍一下基本逻辑。

🧀(1)题目解析：就是分析题目，读懂题目想让我们实现的功能

🧀(2)算法原理：也是最最关键的一点，是我们用动态规划解题的分析过程，也是我们分析问题的具体思路，具体可以分为

🥑[1]状态表示

一般会创建一个数组(dp表)，表中的某个位置的值表示的含义就是状态表示。(感性认知)

怎么确定题目中的状态表示？一般分为三种(之后更新的动态规划相关文章，基本上就是这三种方法确定状态表示)

🙈1*题目要求 

🙉2*经验+要求  以i位置结尾，......（根据题目要求进行描述）

🙊3*分析问题过程中发现重复子问题

🥑[2]状态转移方程 

根据题目推导出有关方程表示 dp[i]

🥑[3]初始化 

为了保证dp表中元素不越界，开始时的几个元素要进行初始化

🥑[4]填表顺序 

在填写当前状态时，所需状态已经填写过了。(一般分为从左向右or从右向左)

🥑[5]返回值

最后返回所需值dp[n]

🧀(3)代码实现

根据上述算法思想，注意一下细节问题，然后写出对应代码。

🧀(4)空间优化 

 一般用滚动数组的方式实现。

在最后用dp表写好具体代码之后，计算出时间和空间复杂度，可以尽可能地优化，减少复杂。但是一般没有这种要求，因此可以适当分析一下，并不是必须的。

🧁题目描述：

示例描述：

 🧀(1)题目解析

泰波那契数列和之前我们熟知的斐波拉契数列比较类似，但是却略有不同。根据题目描述，泰波那契数列是指第n个数是由前三个数的和组成的一个数列

🧀(2)算法原理：

🥑[1]状态表示

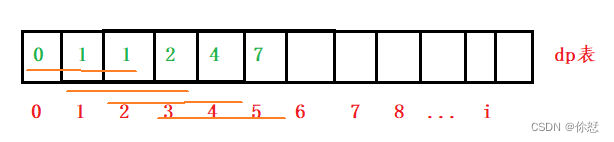
dp[i]表示：以第i个元素结尾，泰波那契数的值

🥑[2]状态转移方程 

根据题目，可以很容易推出T[n]=T[n-3]+T[n-2]+T[n-1]，即状态转移方程

🥑[3]初始化 

因为前三个泰波那契数由题目给出，是无法推出的。因此他们要给初始值：dp[0]=0; dp[1]=dp[2]=1

🥑[4]填表顺序 

很容易看出，后边泰波那契数都是由前边推导出来的，因此填表顺序为从左往右

 🧀(3)代码实现

class Solution {
public:
    int tribonacci(int n) {
        //当n为0,1,2的时候，无法推断，所以需要额外处理
        if(n==0)
            return 0;
        if(n==1||n==2)
            return 1;
         vector<int> dp(n+1);
         dp[0]=0;
         dp[1]=dp[2]=1;
         for(int i=3;i<=n;i++)
         {
             dp[i]=dp[i-3]+dp[i-2]+dp[i-1];
         }
         return dp[n];
    }
};

🥤注意一下细节：在n=0,1,2时，是无法推导出来的，因此需要额外考虑一下！！！

🧀(4)空间优化

可以推出时间复杂度和空间复杂度都为O(N)。用滚动数组方式实现，可以发现，每个泰波那契数都是通过前三个数得到的，那么我们可以将新得到的数向前滚动，从而得到新的数据。这种方式不需要建立dp表，减少空间消耗

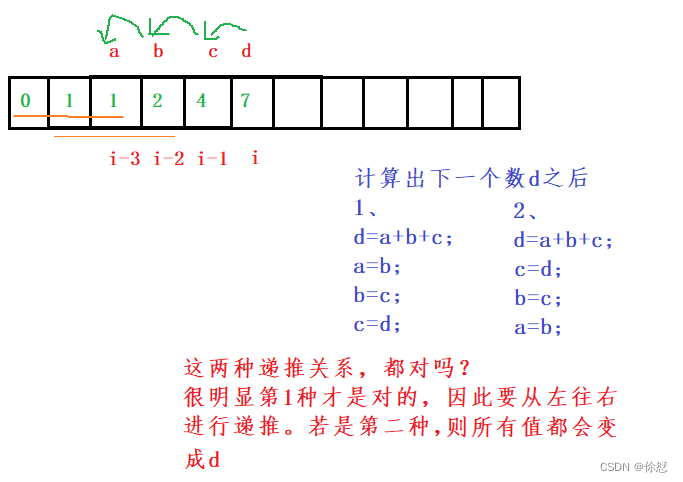
优化后代码表示为：

class Solution {
public:
    int tribonacci(int n) {
        //当n为0,1,2的时候，无法推断，所以需要额外处理
        if(n==0)
            return 0;
        if(n==1||n==2)
            return 1;
        int a,b,c,d;
        a=0;
        b=c=1;
         for(int i=3;i<=n;i++)
         {
            d=a+b+c;
            a=b;
            b=c;
            c=d;
         }
         return d;
    }
};