---

 

概要

 

在机器学习领域中大多数任务通常都与预测（prediction）有关。当我们想预测一个数值时，就会涉及到回归问题。常见的例子包括：预测价格（房屋、股票等）、预测住院时间（针对住院病人等）、 预测需求（零售销量等）。但不是所有的预测都是回归问题。

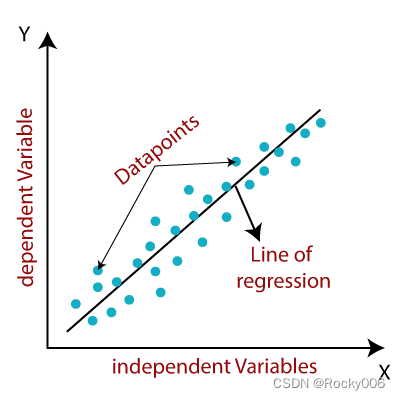
线性回归是一种广泛使用的统计技术，用于理解和建模变量之间的关系。

线性关系不仅仅只能存在 2 个变量（二维平面）。3 个变量时（三维空间），线性关系就是一个平面，4 个变量时（四维空间），线性关系就是一个体，以此类推…

 

 

 

1. 导入数据

首先需要导入要分析的数据。该数据应包含两个变量：自变量（通常表示为“x”）和因变量（通常表示为“y”）。

这里我们使用Matlab自带的数据集“carsmall”

load carsmall;x = Weight;  y = MPG;   

导入后的数据集由以下部分组成：

 

2. 数据预处理

在数据集中存在一些无效数据NaN。在执行线性回归之前，我们将使用 isnan 函数来识别和排除任何 NaN 值。

valid_indices = ~isnan(x) & ~isnan(y);x = x(valid_indices);y = y(valid_indices);

 

3. 可视化数据

在执行线性回归之前，可视化数据通常有助于理解变量之间的关系。

这里使用 MATLAB 的绘图函数来创建数据点的散点图。​​​​​​​

scatter(x, y);xlabel('Independent Variable (x)');ylabel('Dependent Variable (y)');title('Scatter Plot of Data');

 

4. 进行线性回归

这里使用内置的 polyfit 函数执行线性回归操作。

该函数将指定次数的多项式曲线拟合到数据并返回多项式的系数。我们这里要拟合一条直线，所以n取1 。​​​​​​​

coefficients = polyfit(x, y, 1);slope = coefficients(1);intercept = coefficients(2);

polyfit 函数按降序返回多项式的系数。在简单线性回归的情况下，第一个系数表示直线的斜率，第二个系数表示 y 轴截距。

 

5. 绘制回归线

现在有了斜率和截距值，可以在散点图上绘制回归线，以可视化它与数据的拟合程度。​​​​​​​

it = slope * x + intercept;hold on;plot(x, y_fit, 'r');legend('Data', 'Regression Line');

 

6. 评估拟合优度（Goodness of Fit）

要评估回归线的拟合程度，可以计算决定系数（R 平方）值。

MATLAB提供了 corrcoef 函数来计算两个变量之间的相关系数，对其求平方即可得到R平方值。​​​​​​​

correlation_matrix = corrcoef(x, y);correlation = correlation_matrix(1, 2);r_squared = correlation^2;disp(['R-squared: ', num2str(r_squared)]);

运行结果为：

R-squared: 0.73812

R^2越接近1说明误差越小，拟合程度更高。

 

—— end ——

 

欢迎点赞收藏转发，感谢🙏