牛客练习赛113_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ (nowcoder.com)

题意：

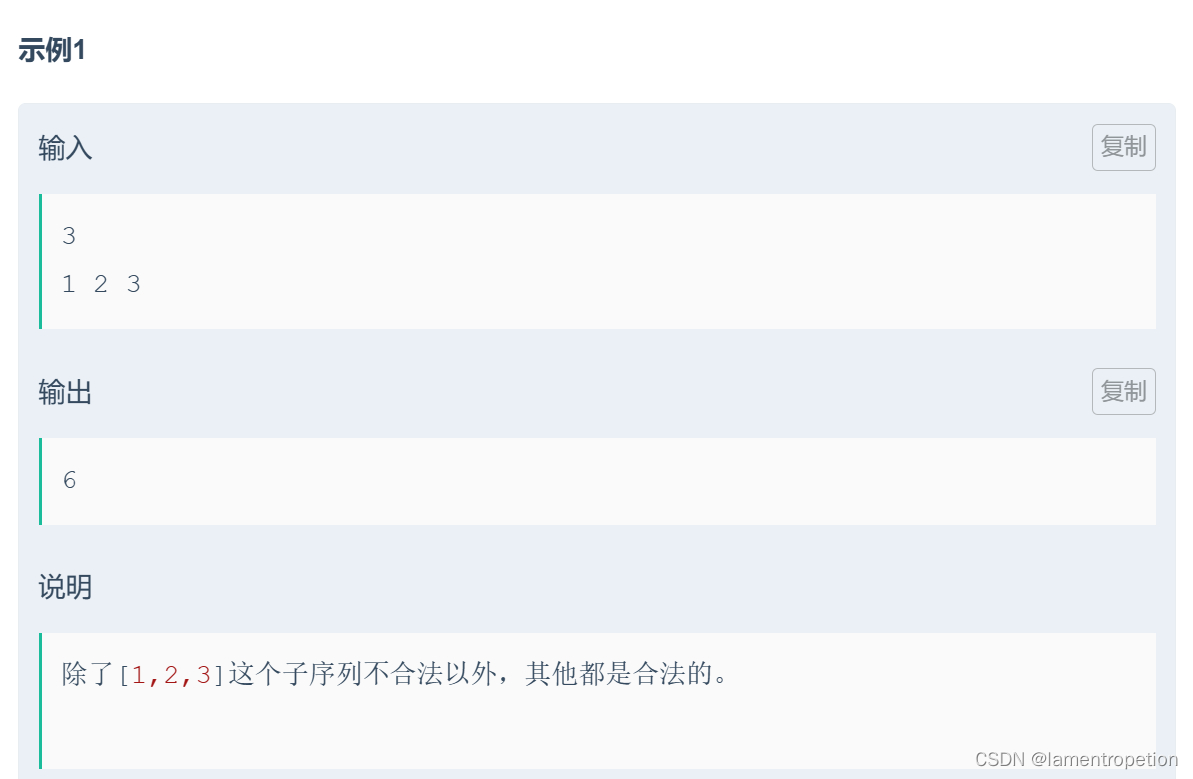
思路：

这道题根本不是子序列DP，因为子序列内部是无序的，这点没意识到

这是问题的easy版本，这种easy版本的题一般都是去考虑暴力枚举

况且数据范围是200，更是暴力

这道题做法是枚举+算组合数

我们去枚举子序列的长度和在子序列中出现次数>=(d+1)/2的元素是哪个，然后再去枚举这个元素在子序列中的出现次数，然后去算组合数

但是这样算出来的答案，对于[1,1,2,2]这种数列会算两次，因此需要容斥一下，减去这部分的贡献

Code：

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int mxn=2e2+10;
const int mxe=1e6+10;
const int mod=1e9+7;
const int Inf=1e18;

vector<int> V;

int N;
int a[mxn],b[mxn];
int C[mxn][mxn];

void C_init(){
    for(int i=0;i<mxn;i++){
        for(int j=0;j<=i;j++){
            if(!j) C[i][j]=1;
            else C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
        }
    }
}
void solve(){
    cin>>N;
    for(int i=1;i<=N;i++){
        cin>>a[i];
        V.push_back(a[i]);
    }
    sort(V.begin(),V.end());
    V.erase(unique(V.begin(),V.end()),V.end());
    for(int i=1;i<=N;i++){
        a[i]=lower_bound(V.begin(),V.end(),a[i])-V.begin()+1;
        b[a[i]]++;
    }
    int M=V.size();
    int ans=0;
    for(int d=1;d<=N;d++){
        for(int x=1;x<=M;x++){
            for(int c=(d+1)/2;c<=d&&c<=b[x];c++){
                if(d<c) continue;
                ans+=C[b[x]][c]*C[N-b[x]][d-c]%mod;
                ans%=mod;
            }
        }
    }
    int res=0;
    for(int d=2;d<=N;d+=2){
        for(int x=1;x<=M;x++){
            for(int y=x+1;y<=M;y++){
                if(b[x]<d/2||b[y]<d/2) continue;
                res+=C[b[x]][d/2]*C[b[y]][d/2]%mod;
                res%=mod;
            }
        }
    }
    cout<<((ans-res)%mod+mod)%mod<<'\n';
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	int __=1;//cin>>__;
    C_init();
    while(__--)solve();return 0;
}