在日常办公中，我们经常遇到需要多次复制文件夹的情况，而繁琐的操作常常令人头疼。但现在，我们为您提供了一款简单易用且高效的解决方案，让您轻松应对复制文件夹的难题，节省宝贵的办公时间！

首先我们要进入文件批量改名高手主页面，并点击“文件智能管理箱”板块并选择“文件批量复制工具”

 第二步：点击“添加文件夹”在弹出来的文件框里选择好要复制的文件夹，进行导入。

 第三步：导入后，单击“添加文件夹”，弹出窗口，选择好复制到的目标文件夹，支持多个，小编测试时只选择了一个

 

 第四步，在复制选项中，将选项切换为“自动编号同名文件”，复制次数自定义，支持1到无限

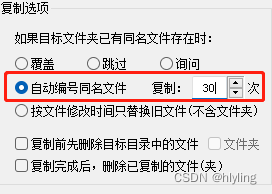
 第五步：全部都设置完成并确认无误之后，单击右下角的“开始复制”按钮

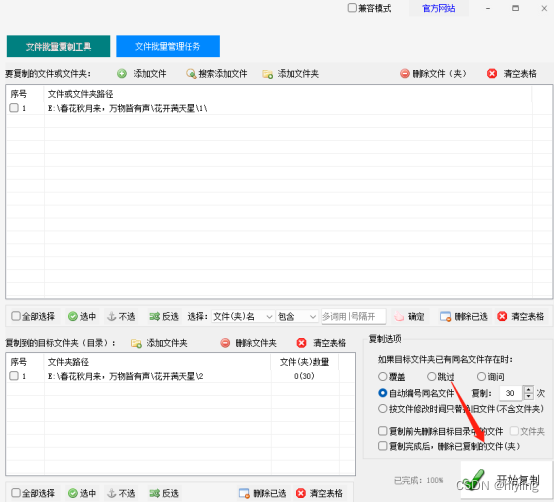
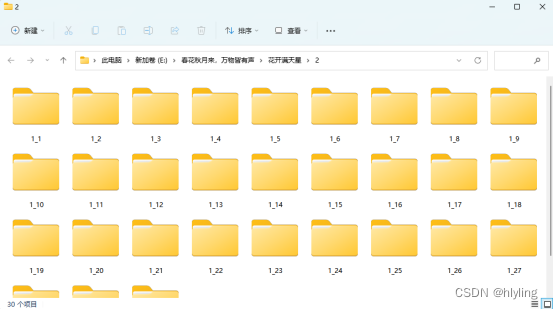
 第六步：等到提示复制完成后，打开文件夹查看，文件夹里的所有文件都复制出了多份，且都保存在同一个文件夹中