数据结构–线索二叉树找前驱后继

中序线索二叉树找中序后继

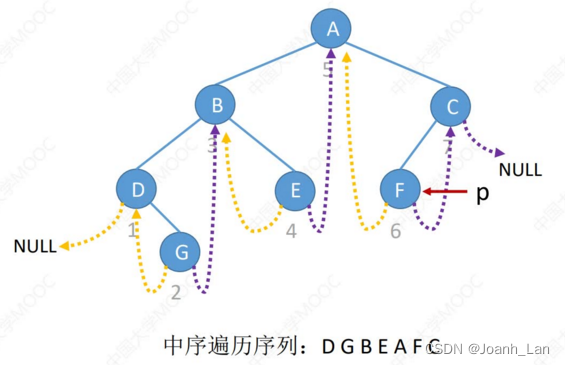
在中序线索二叉树中找到指定结点*p的$中序后继$next
①若p->rtag == 1，则next = p->rchild
②若p->rtag== 0

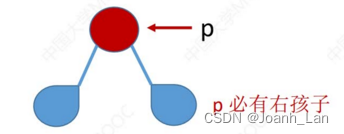
中序遍历――左根右
左根(左根右)
左根((左根右)根右)
next = p的右子树中最左下结点

typedef struct ThreadNode
{
    ElemType data;
    struct ThreadNode *lchild, *rchild;
    int ltag, rtag; //左、右线索标志
}ThreadNode, *ThreadTree; 

//找到以P为根的子树中，第一个被中序遍历的结点
ThreadNode *Firstnode(ThreadNode *p)
{
    //循环找到最左下结点(不一定是叶结点)
    while (p->ltag == 0)   
        p = p->lchild;
    return p;
}
//在中序线索二叉树中找到结点p的后继结点
ThreadNode *Nextnode(ThreadNode *p)
{
    //右子树中最左下结点
    if (p->rtag == 0)   return Firstnode(p->rchild);
    else    return p->rchild;
}
//对中序线索二叉树进行中序遍历(利用线索实现的非递归算法)
void Inorder(ThreadNode *T)
{
    for (ThreadNode *p = Firstnode(T); p != NULL; p = Nextnode(p))
        visit(p);
}

中序线索二叉树找中序前驱

//找到以P为根的子树中，最后一个被中序遍历的结点
ThreadNode *Lastnode(ThreadNode *p)
{
    while (p->rtag == 0) p = p->rchild;
    return p;
}
//在中序线索二叉树中找到结点p的前驱结点
ThreadNode *Prenode(ThreadNode *p)
{
    //左子树中最右下结点
    if (p->ltag == 0)   return Lastnode(p->lchild);
    else    return p->lchild;
}
//对中序线索二叉树进行逆向中序遍历
void RevInorder(ThreadNode *T)
{
    for (ThreadNode *p = Lastnode(T); p != NULL; p = Prenode(p))
        visit(p);
}

在中序线索二叉树中找到指定结点*p的$中序前驱$pre
①若p->ltag == 1，则pre = p->lchild
②若p->ltag == 0

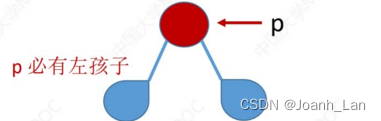
中序遍历―—左根右
(左根右)根右
(左根(左根右))根右
pre =p的左子树中最右下结点

先序线索二叉树找先序后继

先序遍历序列:A B D G E C F

在先序线索二叉树中找到指定结点*p的先序后继next
①若p->rtag == 1，则next = p->rchild
②若p->rtag == 0

先序线索二叉树找先序前驱

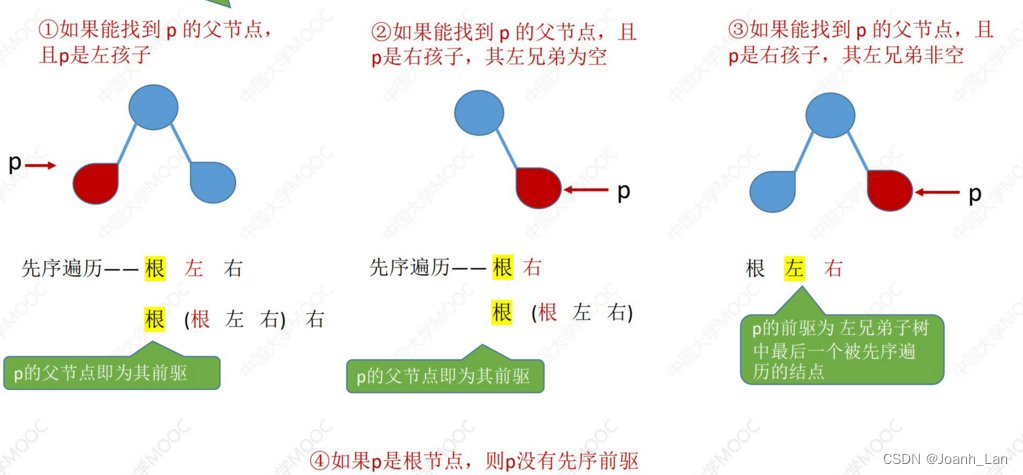
在先序线索二叉树中找到指定结点*p的先序前驱pre
①若p->ltag == 1，则next = p->lchild
②若p->ltag == 0

除非用土办法从头开始先序遍历
先序遍历中，左右子树中的结点只可能是根的后继,不可能是前驱

$改用三叉链表可以找到父节点$

后序线索二叉树找后序前驱

后序遍历序列:G D E B F C A

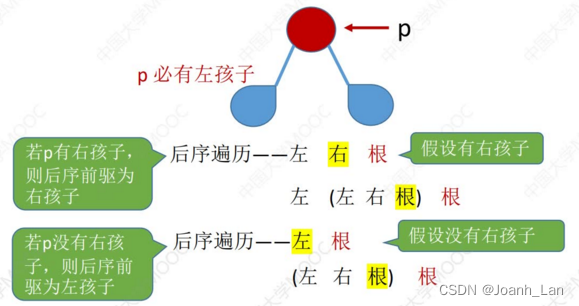
在后序线索二叉树中找到指定结点*p的后序前驱pre
①若p->ltag == 1，则 pre = p->lchild
②若p->ltag == 0

后序线索二叉树找后序后继

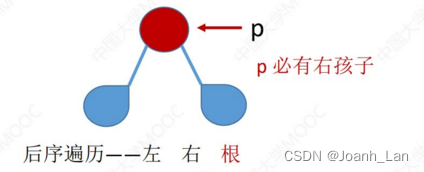
在后序线索二叉树中找到指定结点*p的后序后继next
①若p->rtag == 1，则next = p->rchild
②若p->rtag == 0

除非用土办法从头开始先序遍历

后序遍历中，左右子树中的结点只可能是根的前驱，不可能是后继

$改用三叉链表可以找到父节点$

知识点回顾与重要考点