【动态规划算法】第七题：剑指Offer47.礼物的最⼤价值

news2024/11/16 9:22:23

💖作者：小树苗渴望变成参天大树🎈
🎉作者宣言：认真写好每一篇博客💤
🎊作者gitee:gitee✨
💞作者专栏：C语言,数据结构初阶,Linux,C++ 动态规划算法\🎄

如果你喜欢作者的文章，就给作者点点关注吧！

文章目录

前言

前言

hello,大家好，今天又来更新动态规划的题目了，今天讲的题目在以前的基础上变了一个花样，总体就在状态转移方程的时候有了一点变化，接下来我们开始进入正文进行讲解

第七个题目是礼物的最大价值
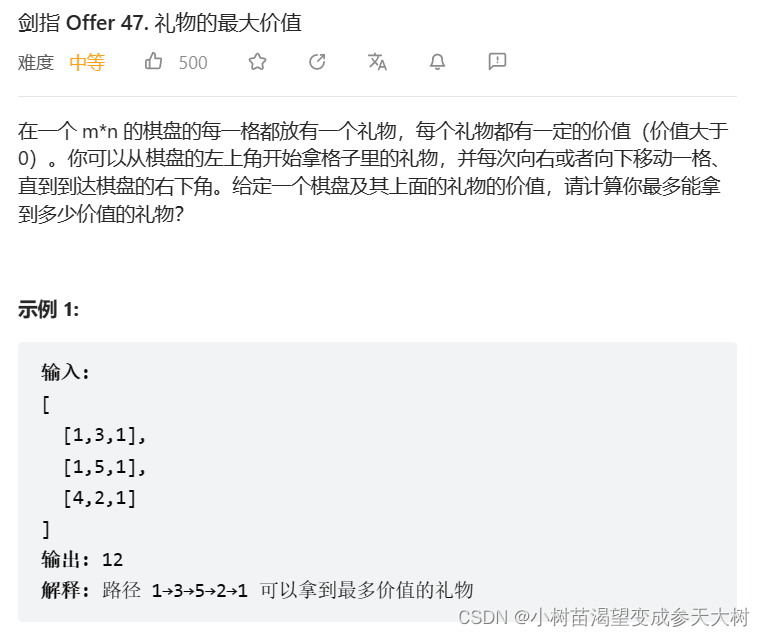
在这里插入图片描述

这个题目讲的非常明确，我就不给大家画图解了，这题传的参数也是一个二维矩阵，所以一会再写的时候要注意下标的映射关系

接下来用动态规划的步骤给大家讲解：

状态表示：经验+题目要求
以(i,j)位置为终点，dp[i][j]表示：到达（i，j）位置时礼物的最大价值
状态转移方程：以最近的状态算出此状态

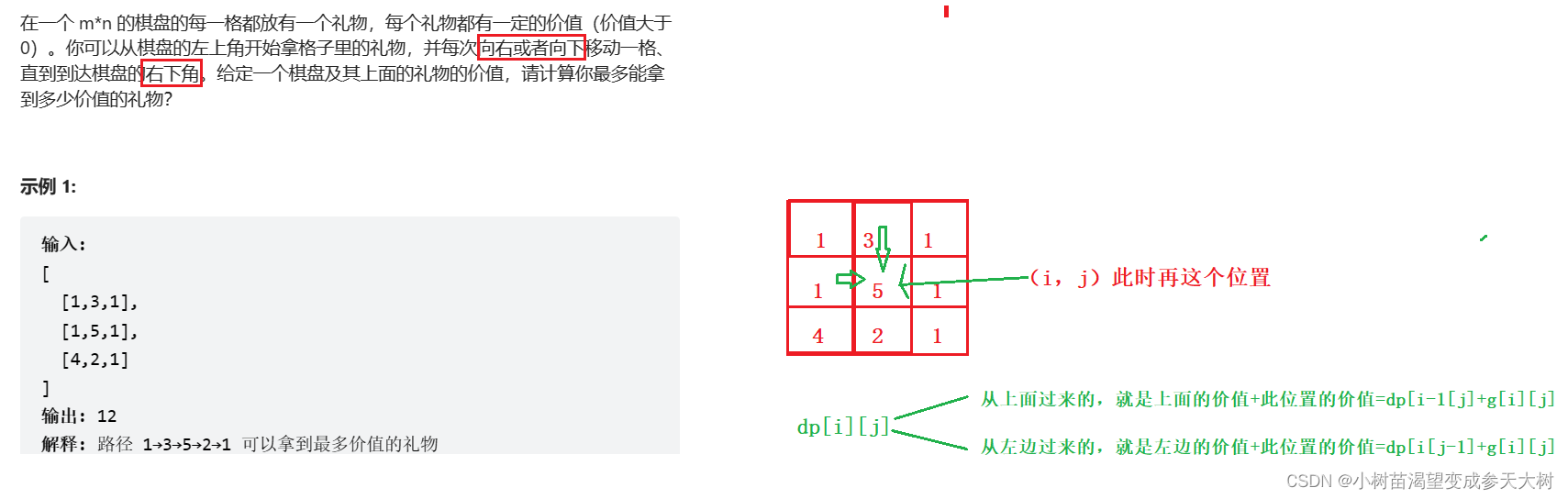
所以dp[i][j]就是两种情况的最大值max(dp[i-1][j]+g[i][j],dp[i][j-1]+g[i][j])
初始化：保证数组不越界，我们的第一行和第一列是从上面或者左边过来的，可能越界，所以还是按照前面的处理边界及初始化问题，构造出虚拟节点

在这里插入图片描述
4. 填表顺序：从上往下填每一行，每一行从左往右
5. 返回值：dp[m][n]
代码实现：

class Solution {
public:
    int maxValue(vector<vector<int>>& grid) {
        //1.创建dp表
        //2.初始化
        //3.填表
        //4.返回值
        int m=grid.size(),n=grid[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+1));
        for(int i=1;i<=m;i++)
            for(int j=1;j<=n;j++)
                dp[i][j]=max(dp[i-1][j]+grid[i-1][j-1],dp[i][j-1]+grid[i-1][j-1]);
        return dp[m][n];
        }
};