0.前言
如有错误,欢迎各位大佬指出。
前置芝士:
-
深度优先搜索
-
广度优先搜索
1.何为高级搜索?
在通常情况下,普通的深搜往往会超时,即使剪枝也无动于衷。对于广搜,我们一旦超时也很难进行优化。
而这时,我们就需要对搜索的形态进行改变,将深搜和广搜进行升级,变形成为各种效率更高的高级搜索算法。
2.折半搜索
主要思想是将整个搜索过程分成两半,分别搜索,最后将两半的结果合并,并最终求得答案。
显然,时间复杂度就是在普通的搜索上,将指数减半。
例题:送礼物
题目意思就是给定一些重量,求出这些重量组合在一起在小于 w w w 的情况下最大是多少。
不难想到一种做法就是先通过爆搜求得前半部分所有能凑出的合法的重量,然后在爆搜后半部分,求得后半部分所有能凑出的合法的数量,并通过二分找到距离 w − w- w− 重量最接近的前半部分的重量。
时间复杂度 2 24 2^{24} 224 再从乘一些玄学二分常数。
但其实这题比较卡常,你需要优化一下常数和你的搜索顺序,即将这个数组从小到大排序再进行搜索。(想一想为什么)
细节见代码。
代码
#include<stdio.h>
#include<algorithm>
#define re register
inline char gc(){static char buf[1000010],*p1=buf,*p2=buf;return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000010,stdin),p1==p2)?EOF:*p1++;}
inline void fast_read(long long &x){x=0;bool f=0;static char s=gc();while(s<'0'||s>'9')f|=s=='-',s=gc();while(s>='0'&&s<='9')x=(x<<3)+(x<<1)+(s^48),s=gc();if(f)x=-x;}
static char buf[1000005];int len=-1;
inline void flush(){fwrite(buf,1,len+1,stdout);len=-1;}
inline void __PC(const char x){if(len==1000000)flush();buf[++len]=x;}
inline void fast_write(long long x){if(x<0)x=-x,__PC('-');if(x>9)fast_write(x/10);__PC(x%10^48);}
#define fr fast_read
#define fw fast_write
#define fs flush
inline int max(const int &a,const int &b){if(a>b) return a;return b;}
#pragma GCC target("sse,sse2,sse3,ssse3,sse4.1,sse4.2,avx,avx2,popcnt,tune=native")
#pragma GCC optimize(2)
//前面都是没用的卡常
#define int long long
int n,W,mid,l,r;
int g[50];
int tot[(1<<24)+1],cnt;//数组不要开小了,开大了也会挂
int ans,i;
void dfs1(const int &x,const int &w)noexcept
{
if(x>(n>>1))
{
tot[++cnt]=w;//将前半部分的统计下来
return;
}
if(w+g[x]<=W)//必须符合条件,否则不要,不然浪费时间
dfs1(x+1,w+g[x]);
dfs1(x+1,w);
}
int upper(const int &x)noexcept//手写二分,优化常数
{
l=1,r=cnt;
while(l<=r)
{
mid=(l+r)>>1;
if(tot[mid]<=x)
l=mid+1;
else
r=mid-1;
}
return l;
}
inline void dfs2(const int &x,const int &w)noexcept
{
if(x>n)
{
int p=upper(W-w);//直接二分找到最接近的那个
ans=max(ans,tot[p-1]+w);
return;
}
if(w+g[x]<=W)
dfs2(x+1,w+g[x]);
dfs2(x+1,w);
}
inline int qunique()noexcept//手写STL优化常数
{
int cntt=0;
for(i=1;i<=cnt;++i)
{
if(tot[i]!=tot[i-1])
tot[++cntt]=tot[i];
}
return cntt;
}
signed main() noexcept
{
fr(W),fr(n);
for(i=1;i<=n;++i)
fr(g[i]);
std::sort(g+1,g+n+1);//优化搜索顺序
dfs1(1,0);
std::sort(tot+1,tot+cnt+1);
cnt=qunique();
dfs2((n>>1)+1,0);
fw(ans);
fs();
return 0;
}
总结:
折半搜索适用于能够将答案分成两半,并合并求解的问题。
其他例题:P2962 [USACO09NOV]Lights G
3.双向搜索
对于一些求两点之间有各种障碍的最短路的问题,由于我们已经确定了起点和终点,所以我们不需要仅仅只是从头开始搜索,而可以从起点和终点两个点同时搜索,这样整个搜索树的规模就会减半。具体来说,就是 2 n 2^n 2n 的复杂度直接减半成为 2 n / 2 2^{n/2} 2n/2 的复杂度。使得平时只能过的 n = 25 n=25 n=25 变成了 n = 50 n=50 n=50。
对于双向搜索,同样有深搜和广搜两种方式。思想比较简单,但代码细节却比较多。
广搜双向搜索例题:八数码问题
题目大意就是给你一个九宫格的初始状态, 0 0 0 是空的,其他的数字都可以向空格移动,让你求得到达给定最终状态的最小步数。
由于我们已知了最终状态和最初状态,所以我们可以想到从两种状态同时开始搜索,并知道他们在中间遇到,至于判重的话,可以采用 H a s h Hash Hash 或者康托展开。然后对于每次操作,直接枚举要移动的数字,看他能移动到哪里,就把所有能移动到的情况放进队列里面即可。
话虽如此,但实现起来真的那么简单吗?
由于是两种状态同时移动,我们不难打出两个队列,然后像普通广搜一样向下移动和压入新节点。即下面这份代码:
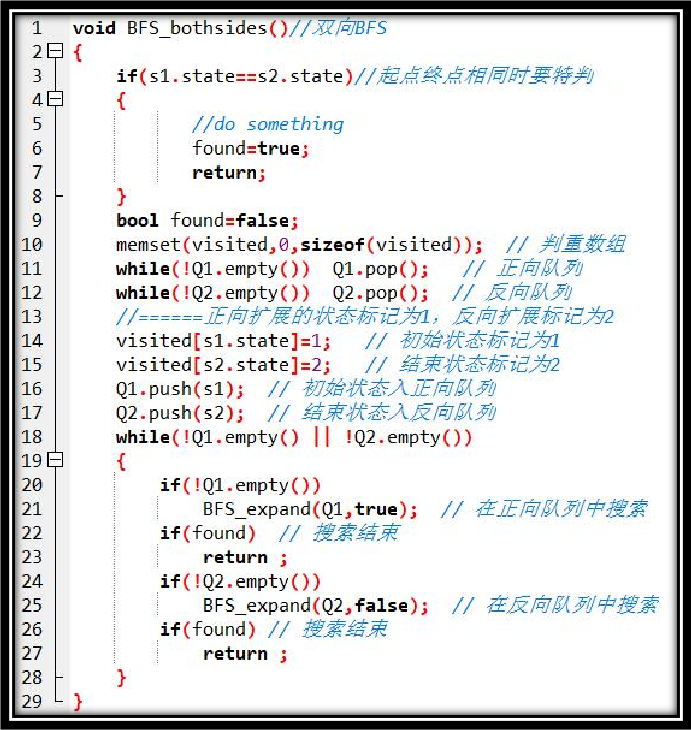
但是,当你实现以后,你却发现这根本就不可能有分。
那为什么会这样呢?
我们先来思考一个问题。我们理想的搜索状态,应该是两个点同时向下遍历,并且遍历到的深度是相同的,这样两种状态才可能刚好在中间相遇而不会出现一个点有 7 7 7 个子节点,但另一个点是一条链到这个点。这种情况就会导致你按照这份代码写,然后种状态的深度才遍历完子节点,而另一种状态都到他家门口了,这肯定不是最优的。
举个例子方便理解(例子与八数码无关,只与双向搜索有关系。)如下图:
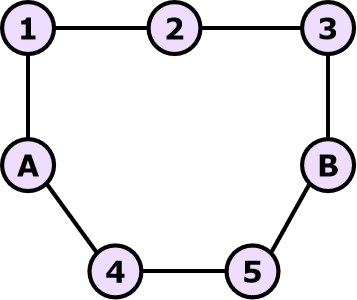
假设 A 为初始状态,B 为结束状态。
显然,首先,对于第一个队列,他会直接压入 1 , 4 1,4 1,4,而另一个队列会直接压入 3 , 5 3,5 3,5,且并没有相遇,直接过。但到了下一步,我们发现,如果按照以上代码运行,我们会直接相遇在 2 2 2,但这并不是最优解。
所以,解决方案就是,定义一个变量代表当前深度,并保证让两者满足在同一深度上进行搜索。但是这样太麻烦了,我们只需要一个队列,来同时搜索起始状态和最终状态才是最简单的写法。
代码(采用了康托展开判重)
#include<bits/stdc++.h>
using namespace std;
int a[11],b[11];
int dis[1000005][2];
int dx[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
struct node//结构体存储当前信息
{
int a[11],bj;
node(int x[11],int b)
{
for(int i=1;i<=9;++i)a[i]=x[i];
bj=b;
}
};
std::queue<node> p;
inline int contor(int a[])
{
int ans=0;
for(int i=1;i<=9;++i)
{
int tot=1,bj=0;
for(int j=i+1;j<=9;++j)
{
tot*=(j-i);
if(a[j]<a[i])
bj++;
}
ans+=tot*bj;
}
return ans;
}
inline int bfs()
{
p.push(node(a,0));
p.push(node(b,1));//采用一个队列的话,需要压入当前节点属于那个状态
dis[contor(a)][0]=1,dis[contor(b)][1]=1;
while(!p.empty())
{
node x=p.front();
p.pop();
int y[4][4],z=x.bj;
for(int i=1;i<=9;++i)
y[int(ceil(i/3.0))][(i-1)%3+1]=x.a[i];//运用了一些自己推出来的坐标
int q=contor(x.a);
if(dis[q][!z]) return dis[q][!z]+dis[q][z]-2;//如果另一个状态也枚举到了这个点,那就不用再继续了
for(int i=1;i<=3;++i)
{
for(int j=1;j<=3;++j)
{
for(int k=0;k<=3;++k)
{
//暴力搜索
int xx=i+dx[k][0],yy=j+dx[k][1];
if(xx>0&&xx<4&&yy>0&&yy<4&&y[xx][yy]==1)
{
swap(y[i][j],y[xx][yy]);
int b[10];
for(int l=1;l<=3;++l) for(int m=1;m<=3;++m) b[(l-1)*3+m]=y[l][m];
if(dis[contor(b)][z]){swap(y[i][j],y[xx][yy]);continue;}
p.push(node(b,z));
dis[contor(b)][z]=dis[q][z]+1;
swap(y[i][j],y[xx][yy]);
}
}
}
}
}
return -1;
}
int main()
{
for(int i=1;i<=9;++i) cin>>a[i],a[i]++;
for(int i=1;i<=9;++i) cin>>b[i],b[i]++;
printf("%d",bfs());
return 0;
}
总结
主要就是细节,搞清楚自己代码的每一步的作用,这样能防出错。
其他例题:P2324 [SCOI2005]骑士精神
4.迭代加深
对于一颗深搜的搜索树,由于我们是深度优先遍历,所以我们会将每一种情况搜到最深,然后再去考虑另一种情况。但是,对于一个节点,他的搜索顺序在很后面而深度却很浅,亦或者我们要求完成某种状态的最小深度,那我们不难想到一种做法,就是去限制深度,然后遍历完所有小于这个深度的点。然后深度从 0 0 0 开始,一直加,直到我们找到答案为止。这就是迭代加深的具体思想。
例题:#8632. 埃及分数
显然,看到这个题,我们不难想到直接用迭代加深来限制搜索然后每次枚举值域进行爆搜,最后到达深度的时候 check 一下。
但显然,值域太大了,因此我们需要在枚举值域的时候一些限定。
为了方便,我们可以让每次枚举下一个的时候,保证单调递增,则我们就有了枚举值域的下界,然后在通过分数减来求得上界,这样就能缩小不少的复杂度。
#include<bits/stdc++.h>
using namespace std;
#define gcd(a,b) __gcd(a,b)
#define int long long
int m;
int a,b,ansans=LONG_LONG_MAX;
int p[100005],ans[100005];
bool dfs(int deep,int a,int b)
{
if(deep>m)
{
if(a==0)
{
if(p[m]<ansans)
{
ansans=p[m];
for(int i=1;i<=deep-1;++i)
ans[i]=p[i];
}
return true;
}
return false;
}
bool flag=false;
for(int i=max(p[deep-1]+1,b/a);i<=(m-deep+1)*b/a;++i)
{
int fm=b*i,fz=a*i-b,gcdgcd=gcd(fm,fz);
fm/=gcdgcd,fz/=gcdgcd;
p[deep]=i;
if(dfs(deep+1,fz,fm))
flag=true;
}
return flag;
}
signed main()
{
cin>>a>>b;
do
{
++m;
if(dfs(1,a,b))
{
for(int i=1;i<=m;++i)
{
printf("%lld ",ans[i]);
}
break;
}
}
while(1);
return 0;
}
5.双端队列搜索
有些时候,由于我们搜索每次加深深度时,他的代价不一定为 1 1 1。比如说对于图在有边权的情况下,每次向下遍历一个点的代价就不为 1 1 1。但对于某种特殊的情况,我们加深深度的时候,他的代价为 1 1 1 或者 0 0 0 而不为其他时,我们不一定就不能广搜,而是可以将普通的广搜队列换成双端队列,然后做如下修改:
-
当我们向下加深的代价为 0 0 0 时,显然,你再往下的答案深度不会大于队头的答案深度,所以可以直接将新的节点放在队头。
-
对于向下加深的代价为 1 1 1 时,那我们大可将其看成与普通广搜一样,直接放在队尾。
不难想明白,这样操作仍然能满足队里从头到尾的答案深度从小到大,也就满足广搜的基本条件了。
双端队列搜索例题:最少转弯问题
显然,我们可以将当前行走的方向, x x x 坐标, y y y 坐标放入广搜队列,然后,改变方向的边权为 1 1 1,不改变方向的边权为 0 0 0,然后就变成双端队列搜索了。
代码
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[1005][1005];
int sc,sy,tx,ty;
int vis[1005][1005][4];
deque<int> p,q,r;
int dx[4][2]={{0,1},{-1,0},{0,-1},{1,0}};
int bfs()
{
int ans=INT_MAX;
for(int i=1;i<=4;++i)
p.push_front(sc),q.push_front(sy),r.push_front(i-1),vis[sc][sy][i-1]=1;
while(!p.empty())
{
int x=p.front(),y=q.front(),z=r.front();
p.pop_front(),q.pop_front(),r.pop_front();
if(x==tx&&y==ty) ans=min(ans,vis[x][y][z]-1);
for(int i=0;i<4;++i)
{
int xx=x+dx[i][0],yy=y+dx[i][1];
if(xx<1||yy<1||xx>n||yy>m) continue;
if(vis[xx][yy][i]) continue;
if(a[xx][yy]==1) continue;
if(i==z)
vis[xx][yy][i]=vis[x][y][z],p.push_front(xx),q.push_front(yy),r.push_front(i);
else
vis[xx][yy][i]=vis[x][y][z]+1,p.push_back(xx),q.push_back(yy),r.push_back(i);
}
}
return ans;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i)
{
for(int j=1;j<=m;++j)
{
scanf("%d",&a[i][j]);
}
}
cin>>sc>>sy>>tx>>ty;
cout<<bfs();
}
6.优先队列搜索
与双端队列类似,这也是一种广搜的变形,并且优先队列搜索包含了双端队列搜索的适用范围。
我们知道,对于广搜,在通常情况下我们会认为第一次遍历到一个点就会得到这个点的最优答案,然后不会让这个点再被遍历到一次。(少部分情况不满足这个条件,比如对于 SPFA就不满足,但相应的,效率就会变低)因此,我们就尝试让队列里面,满足从队头到队尾逐渐更优。这样,我们就能够做到第一次遍历到一个点,他就会得到最优解,而不会遍历到第二次,从而来降低一个复杂度。(当然,由于是优先队列,会多一个
l
o
g
log
log。)
但是,对于优先队列搜索,它有一个限制,就是它只适用于每次加深深度代价为非负数的情况。为了方便讲述,我们在这里以最短路为例。
假设我们第一次遍历到的点他的最短路为
y
y
y。但是这个点与另一个点有一个负边权为
z
z
z,且另一个点的最短路为
x
x
x。由于
z
z
z 是负的,所以
x
+
z
x+z
x+z 可能会比
y
y
y 更小,从而也就不满足第一次遍历到一个点就会求得他的最优解这个条件。因此,在这种情况下,我们就需要让一个点多背遍历到几次,也就形成了 SPFA 算法。但显然,对于边权都是非负数的情况,那就肯定不存在这种形态。(自己思考)
可以发现,优先队列搜索就是估价函数为 0 0 0 的 A*搜索。所以就没有例题啦。
7.A*算法
A ∗ * ∗ 搜索算法(英文:Asearch algorithm,A读作 A-star),简称 A算法,是一种在图形平面上,对于有多个节点的路径求出最低通过成本的算法。它属于图遍历(英文:Graph traversal)和最佳优先搜索算法(英文:Best-first search),亦是 BFS 的改进。(粘自 oi-wiki)
他的前提条件是必须存在一个起始状态或者结束状态。
先说一下 A_star 算法的具体操作。(别问我为什么写成 A_star,问就是 A* 他会变斜体,不会 markdown…)。
具体操作就是建立一个优先队列来代替普通的队列,然后写一个估价函数 h ( x ) h(x) h(x),来预估到终点可能需要的代价,并且必须保证这个代价要小于真实代价,然后将当前代价 g ( x ) g(x) g(x) 与 h ( x ) h(x) h(x) 加在一起放进优先队列,每次取出最优的,并更新相邻节点的状态。
下面会证明,第一次遍历到一个点就一定能求出最优解,从而保证复杂度。
我们先定义一些名词:当我们到达点 n n n 时,已经付出的代价为 g ( n ) g(n) g(n),这是我们已经知道的,然后假设有上帝,告诉我们这条路到最优解还差 h ∗ ( n ) h*(n) h∗(n),但是没有上帝,我们仅仅用这个节点下一步路径的最短值作为永远的相对小值 h ( n ) h(n) h(n) 估计值 h ∗ ( n ) h*(n) h∗(n)。我们设从原点到点n的代价为 f ∗ ( n ) = g ( n ) + h ∗ ( n ) f*(n)=g(n)+h*(n) f∗(n)=g(n)+h∗(n),代表着上帝告诉我们如果选了n,那么最优解是 f ∗ ( n ) f*(n) f∗(n),那么有 f ( n ) = g ( n ) + h ( n ) < = f ∗ ( n ) f(n)=g(n)+h(n)<=f*(n) f(n)=g(n)+h(n)<=f∗(n)( f ( n ) f(n) f(n) 是我们实际计算得到的,并且加入堆进行 b e s t − f i r s t best-first best−first 比较的)
简单来讲,就是下界不必说,你找到的这个路因为估计值小于其他的,而且到了最后一步了,所以路径也小于其他的估计值,传递一下,进而小于其他的准确值,也就是该路是最短的。进而得证。
感性的理解一下,毕竟证明也不是很重要,如要参考更严格的证明,见此。
例题:#489. 第k短路
显然,这个题的每个点的 A* 函数就是每个点到终点的最短路,然后枚举到一个点的第 k k k 次,就能得到它的第 k k k 短路。
代码
#include<bits/stdc++.h>
using namespace std;
int n,m,s,t,k;
int fst[100005],cnt;
int star[100005];
struct node
{
int tar,num,nxt;
}arr[500005];
void adds(int x,int y,int z)
{
arr[++cnt].tar=y,arr[cnt].num=z,arr[cnt].nxt=fst[x],fst[x]=cnt;
}
bool vis[100005];
int dis[100005];
priority_queue<pair<int,int> >p;
void A_star()
{
memset(dis,0x3f,sizeof(dis));
p.push(make_pair(0,t));
vis[t]=1;dis[t]=0;
while(!p.empty())
{
int x=p.top().second;
p.pop();
for(int i=fst[x];i;i=arr[i].nxt)
{
int y=arr[i].tar,z=arr[i].num;
if(dis[y]>dis[x]+z)
{
dis[y]=dis[x]+z;
if(!vis[y])
{
vis[y]=1;
p.push(make_pair(-dis[y],y));
}
}
}
}
for(int i=1;i<=n;++i)
{
star[i]=dis[i];
}
}
void bfs()
{
while(!p.empty()) p.pop();
q.push(make_pair(-star[s],s));
memset(vis,0,sizeof(vis));
while(!q.empty())
{
int x=q.top().first,y=q.top().second-star[x];
q.pop();
vis[x]++;
if(x==t&&vis[x])
for(int i=fst[x];i;i=arr[i].nxt)
{
int z=arr[i].tar,w=arr[i].num;
d
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
adds(x,y,z);
}
}
8.IDA*算法
可以看做是 A* 算法的一种 dfs 的实现形式。你可以看做是迭代加深的一种剪枝优化。
首先,你需要迭代加深来限制深度,并且你需要终点来求得和满足 A* 条件的估价函数。
由于你限制了深度,且有了比现实更乐观的估价函数,所以如果当前深度加上估价都会超过限制深度的话,那在现实不乐观的情况下就一定在限制深度内达成不了目标,就可以直接返回不行了。(就是一种剪枝)
例题:编辑书稿
题意大致就是给你一个 n n n 的排列,然后你可以选择一个区间,移动他到任意一个位置,让你求出将序列变为单调递增序列,需要移动的最少步数。
不难想到一种迭代加深的搜索,即限定搜索深度,然后枚举修改区间的左右端点,以及修改的位置,然后再用一个 O ( n ) O(n) O(n) 的时间复杂度来模拟操作。
但你发现,你获得了 TLE 33 分的好成绩,所以我们现在需要进行一些剪枝,那很明显就需要打出一个
A
∗
A*
A∗ 函数了。
我们可以先限定一个条件,及 a [ i ] = a [ i − 1 ] + 1 , a [ 0 ] = 1 a[i]=a[i-1]+1,a[0]=1 a[i]=a[i−1]+1,a[0]=1,显然,对于最终状态,我们有这个条件的满足数量为 n n n。假设当前状态满足这个条件的数量为 x x x。显然,对于一次区间为 [ l , r ] [l,r] [l,r] 的操作,将其移至 x x x 前面,那么我们至多可以让 i = l , i = x , i = x − 1 i=l,i=x,i=x-1 i=l,i=x,i=x−1 3 个新的 i i i 满足条件。
也就是说,我们从当前状态到最终状态在最乐观的情况下还要操作 n − x 3 \frac{n-x}{3} 3n−x 次。也就打出了我们的估价函数。
这样的话其实已经可过了,但是如果你想进一步优化,你可以打一个链表,在你移动的时候,你只需要修改 l − 1 , l , r , r + 1 , x − 1 , x l-1,l,r,r+1,x-1,x l−1,l,r,r+1,x−1,x 这 6 6 6 个下标的链表值,也就实现了 O ( 1 ) O(1) O(1) 的修改。
代码
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[13],b[13];
bool check()//判断是否到达最终状态
{
for(int i=1;i<=n;++i) if(a[i]<a[i-1]) return false;
return true;
}
int h()//A*
{
int cnt=0;
for(int i=1;i<n;++i) if(a[i]!=a[i+1]-1) cnt++;
return (cnt+2)/3;
}
bool id(int deep)
{
// cout<<deep<<endl;
// for(int i=1;i<=n;++i) cout<<a[i]<<" ";
// cout<<endl;
if(check()) return true;
if(deep+h()>m+1) return false;
int c[13];
for(int r=1;r<=n;++r)//右端点
{
for(int l=1;l<=r;++l)//左端点
{
for(int i=1;i<l;++i)//枚举位置
{
for(int j=1;j<=n;++j) c[j]=a[j];
int cnt=i-1;
// for(int j=1;j<i;++j) a[++cnt]=c[j];
for(int j=l;j<=r;++j) a[++cnt]=c[j];
for(int j=i;j<l;++j) a[++cnt]=c[j];
for(int j=r+1;j<=n;++j) a[++cnt]=c[j];
if(id(deep+1)) return true;
for(int j=1;j<=n;++j) a[j]=c[j];
}
}
}
return false;
}
int main()
{
int t=0;
while(~scanf("%d",&n))
{
if(!n) return 0;
t++;
for(int i=1;i<=n;++i) scanf("%d",&a[i]),b[i]=a[i];
m=0;
while(1)
{
for(int i=1;i<=n;++i) a[i]=b[i];
if(m>=6||id(1))
{
printf("Case %d: ",t);
cout<<m<<endl;
break;
}
++m;
}
}
}
总结
这玩意估价函数很重要,另外,你可以写一个操作次数上限,到达上限就直接返回真,实测有效,防止TLE大法!
其他例题:#6026. 回转游戏