1、迭代,链表反转
listNode prev = null, next, curr = head;
while (curr != null) {
next = curr.next;
curr.next = prev;
curr = next;
prev = curr;
curr = next;
}
return prev;
2、递归,链表反转
/*// 两个节点时
head.next.next = head;
head.next = null;
*/
// 多个节点时
listNode recursion(listNode head) {
if (head == null || head.next == null) {
return head;
}
listNode new_head = recursion(head.next);
head.next.next = head;
head.next = null;
return new_head;
}
3、统计素数的个数,埃筛法
// 暴力算法
// 遍历 [2, n),判断每一个书是否为素数
// x 素数判断,查找 [2, x),是否有能够整除 x 的数
// 埃筛法
// 遍历到一个素数,对素数进行倍增,倍增的结果是合数,遍历的时候,这些合数直接跳过
vector<bool> isPrime(n, 0);
int cnt = 0;
for (int i = 2; i < n; i++) {
if (!isPrime[i]) {
cnt ++;
for (int j = 2 * i; j < n; j += i) {
// 这里可以优化,去掉重复遍历
// for (int j = i * i; j < n; j += i)
isPrime[j] = 1;
}
}
}
return cnt;
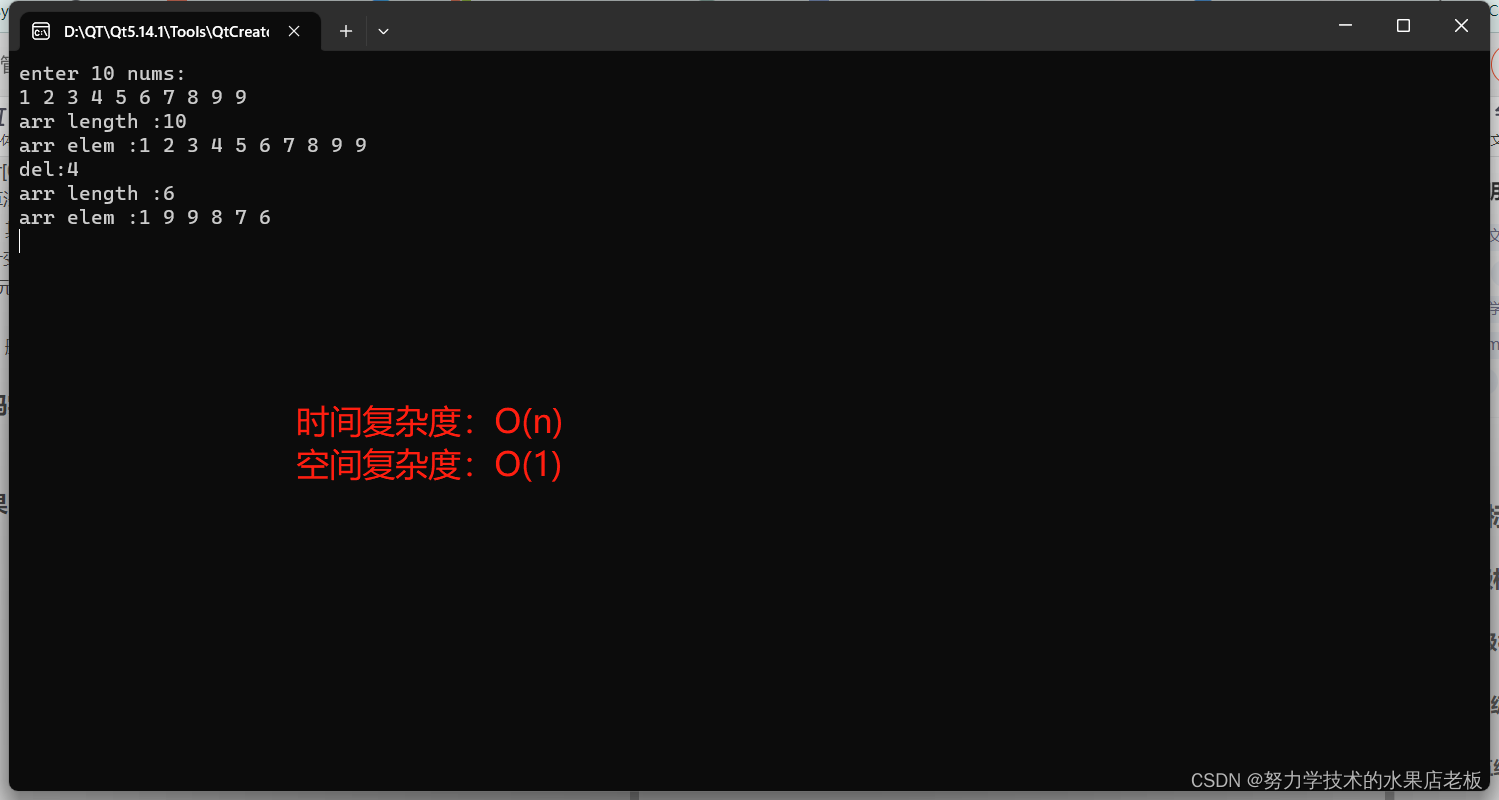
4、删除排序数组中的重复项,双指针
// 快慢指针
// 不相等,一起往后移动
// 相等,快指针移动,慢指针不移动
if (!nums.size()) {
return 0;
}
int i = 0;
for (unsigned j = 1; j < nums.szie(); j++) {
if (nums[j] != nums[i]) {
i++;
nums[i] = nums[j];
}
}
return i + 1;
5、二分法
// 暴力遍历是万能的,也可以使用二分法
6、牛顿迭代
// n = x * x
// (n / x + x) / 2 = placeholder
// (n / placeholder + placeholder) / 2
7、动态规划
// dp 数组,迭代
// 递归
// 双指针减小空间复杂度
// 首尾相连:第一个和最后一个二选一,在[0, n-2] 和 [1, n - 1],分别求最大值,再取二者最大值
// 二叉树结构,深度优先遍历,递归
8、寻找数组的中心下标
// 左边元素的和等于右边的元素的和
// 数组求和,sum 整个数组的求和
// total,累加元素
// 从左往右遍历数组, sum 递减,和当前的 total 比较,当二者相等时,即为所求位置
9、数组中三个数的最大乘积
// 先对数组排序
// 最小的两个元素和最大的一个元素的乘积,最大的三个元素的乘积,两者的较大者就是结果
// 原因是如果有负数,那么最小的数一定是负数,如果有正数,那么最大的数一定是正数
// 线性扫描
// 在数组中找到最大的三个值和最小的两个值即可
// 找最小的两个
int min1 = INT_MAX, min2 = INT_MAX;
int max1 = INT_MIN, max2 = INT_MAX, max3 = INT_MAX;
for(auto x : nums) {
if (x < min1) {
min2 = min1;
min1 = x;
} else if (x < min2) {
min2 = x;
}
if (x > max1) {
max3 = max2;
max2 = max1;
max1 = x;
} else if (x > max2) {
max3 = max2;
max2 = x;
} else if (x > max3) {
max3 = x;
}
}
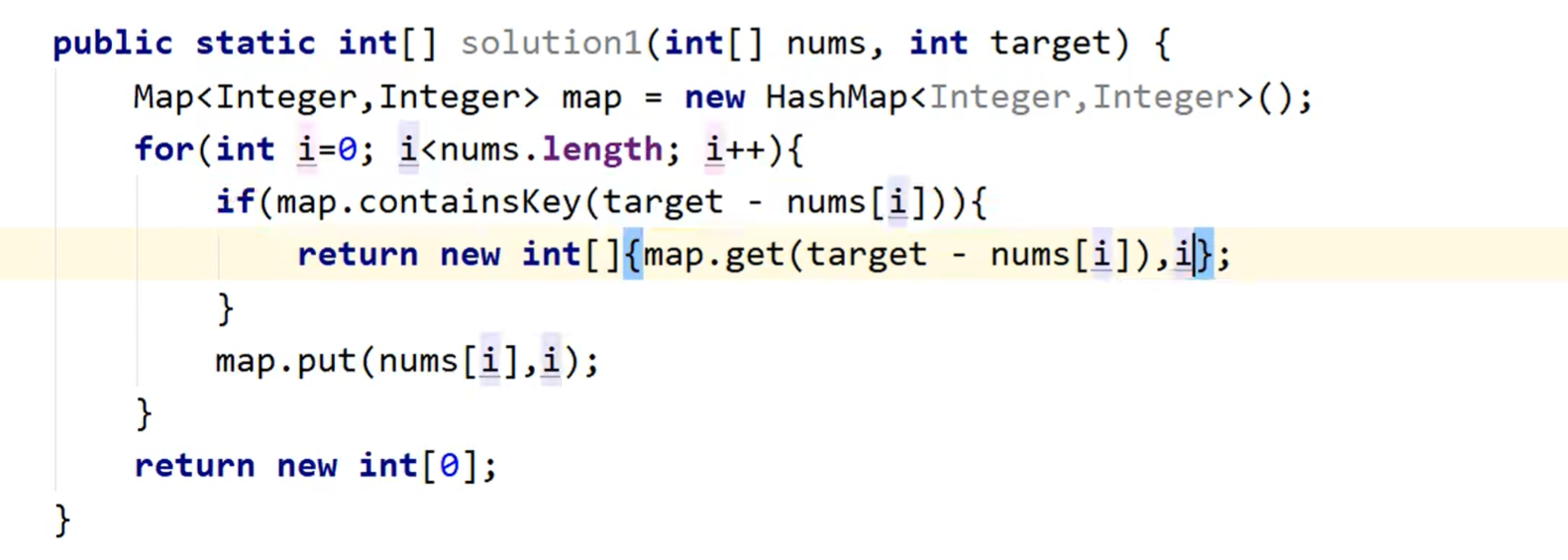
10、两数之和
// 无序数组
// 暴力遍历
// 另一种方法,map 打标记
// 有序数组
// 二分查找,遍历数组,在该元素 x 开始的后面的子数组使用二分法来查找 target - x,直到找到 满足条件的 x 为止
// 双指针,分别从数组开头和结尾开始,根据两者相加与 target 的关系:若大于,右指针左移;小于,左指针右移。直到两指针相等,或者找到结果,停止
11、斐波那契数列
// 暴力解法,计算到第 N 位为止
// 递归
// 暴力解法,去重递归
// 每一个节点的值都存储起来,减少重复运算
// 双指针迭代,只需要保存两个值即可
if (!num) {
return 0;
}
if (num == 1){
return 1;
}
int low = 0, high = 1;
for (int i = 2; i < num; i++) {
int sum = low + high;
low = high;
high = sum;
}
return high;
递归:

去重递归:
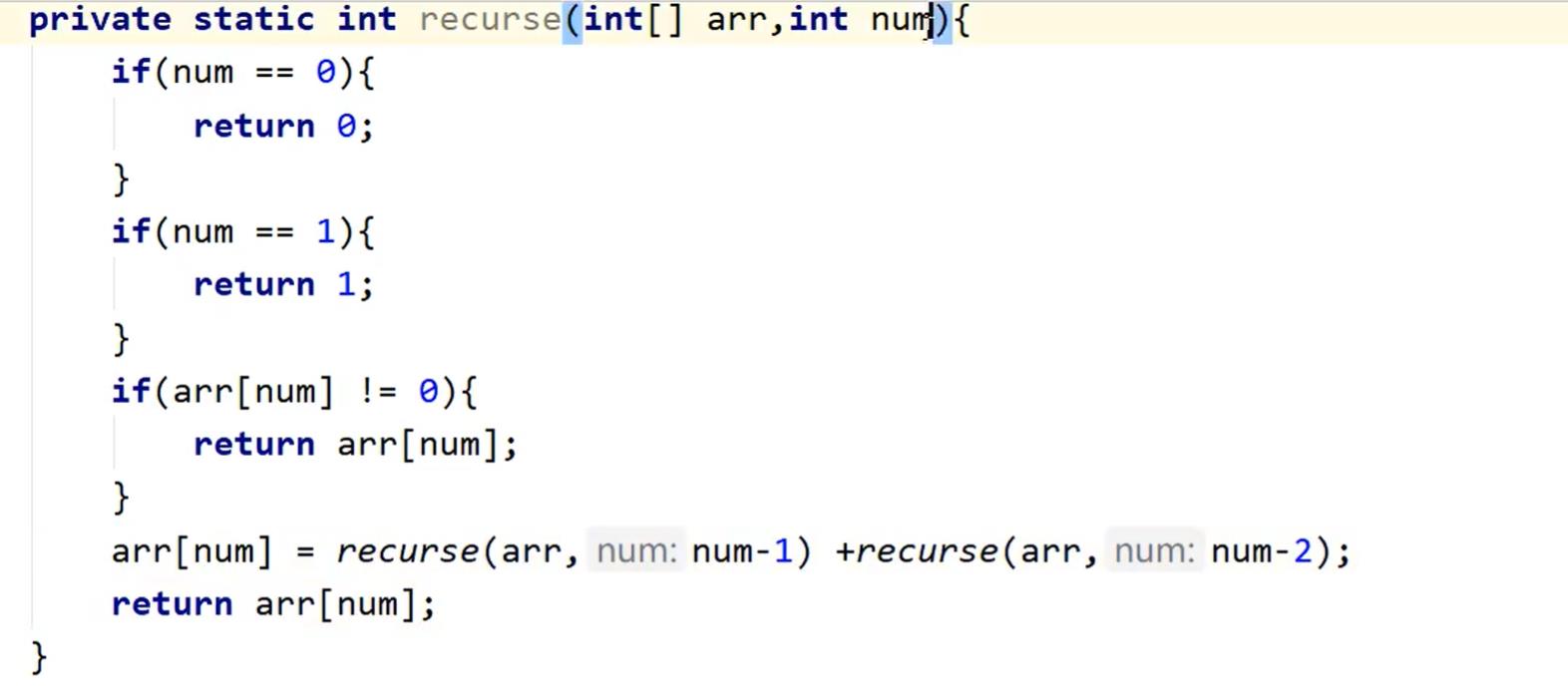
12、排列硬币
// 直接用 N 从 1 开始减,直到 i > n
// 二分,假设可以放 N 行,在 [0,n] 中间二分查找 x,直到 (x*x+x) / 2
// 牛顿迭代
13、合并两个有序数组
// 数组合并,再排序
// 同时遍历两个数组,按顺序合并进一个新数组
// 同时倒序遍历两个数组,从 nums1 的尾部开始放置
14、环形链表
// 判断链表中是否存在环
// 使用 set,来存放每一个访问到的节点,若出现重复的节点,那么就存在环
std::set<ListNode> hashSet();
// 快慢指针法
// 若存在环,两个指针会相遇
if (head == null || head.next == null)
return false;
ListNode slow = head;
ListNode quick = head.next;
while(slow != quick) {
if (quick == null || quick.next == null)
return false;
slow = slow.next;
quick = quick.next.next;
}
return ture;
15、子数组最大平均数,滑动窗口
// 双指针,滑动窗口
int max_sum = INT_MIN;
int start = 0, end = k - 1;
int sum = 0;
for (int 1 = 0; i < k; i++) {
sum += nums[i];
}
start++;
end++;
for ( ; end < nums.size(); start++, end++) {
max_sum = max_sum + nums[end] - nums[start];
if (max_sum < sum)
max_sum = sum;
}
return max_sum * 1.0 / k;
16、在 1000 瓶药中找出毒药
// 利用二进制表示来做,还有多个变种问题
17、二叉树最小深度,深度优先/广度优先
// 深度优先,先找到每一个叶子结点,进入叶子节点的深度,再从叶子结点往上遍历,直到根节点,求出每一个节点的深度,求出深度的最小值
int minDepth(TreeNode root) {
if (root == null) {
return 0;
}
// 递归
if (root.left == null || root.right == null)
return 1;
int min = INT_MAX;
if (root.left != null) {
min = max(minDepth(root.left),min);
}
if (root.right != null)
min = max(minDepth(root.right), min);
return min + 1;
}
// 广度优先,根节点开始向下找,逐层找,找到叶子结点为止
// 广度优先,使用队列存放节点,先进先出
int minDepth(TreeNode root) {
if (root == null)
return 0;
std::queue<TreeNode> q;
root.depth = 1;
q.push(root);
while(!q.empty()){
TreeNode currNode = queue.front();
q.pop();
if (currNode.left == null || currNode.right == null)
return currNode.depth;
if (currNode.left != null) {
currNode.left.depth = currNode.depth + 1;
q.push(currNode.left);
}
if (currNode.right != null) {
currNode.right.depth = currNode.depth + 1;
q.push(currNode.right);
}
}
return 0;
}
18、最长连续递增子序列,贪心法
// 数组未排序,子序列下标连续
int findLength(std::vector<int> nums) {
int start = 0;
int maxLength = 0;
for (int i = 1; i < nums.size(); i++) {
if (nums[i] <= nums[i - 1]) {
start = i;
}
maxLength = max(i - start + 1, maxLength);
}
return maxLength;
}
19、柠檬水找零,贪心法
// 5 块不用找零,10块只能找5 块,20 优先找 10 + 5
bool change(std::vector<int> bills){
int five = 0, ten = 0;
for (int i = 0; i < bills.size(); i++) {
if (bills[i] == 5) {
five++;
} else if (bills[i] == 10) {
if (five == 0)
return false;
five--;
ten++;
} else {
if (five > 0 && ten > 0) {
five--;
ten--;
} else if (five >= 3) {
five -= 3;
} else {
return false;
}
}
}
return true;
}
20、求三角形最大周长,贪心法
// 组成三角形:三边关系
// 数组排序,找最大的三个数,判断能否组成三角形,若不行,则往前滑动一个元素,直到符合三角形三边关系即可
// 在数组排序之后,取元素的时候,从后往前取