2271. 毯子覆盖的最多白色砖块数

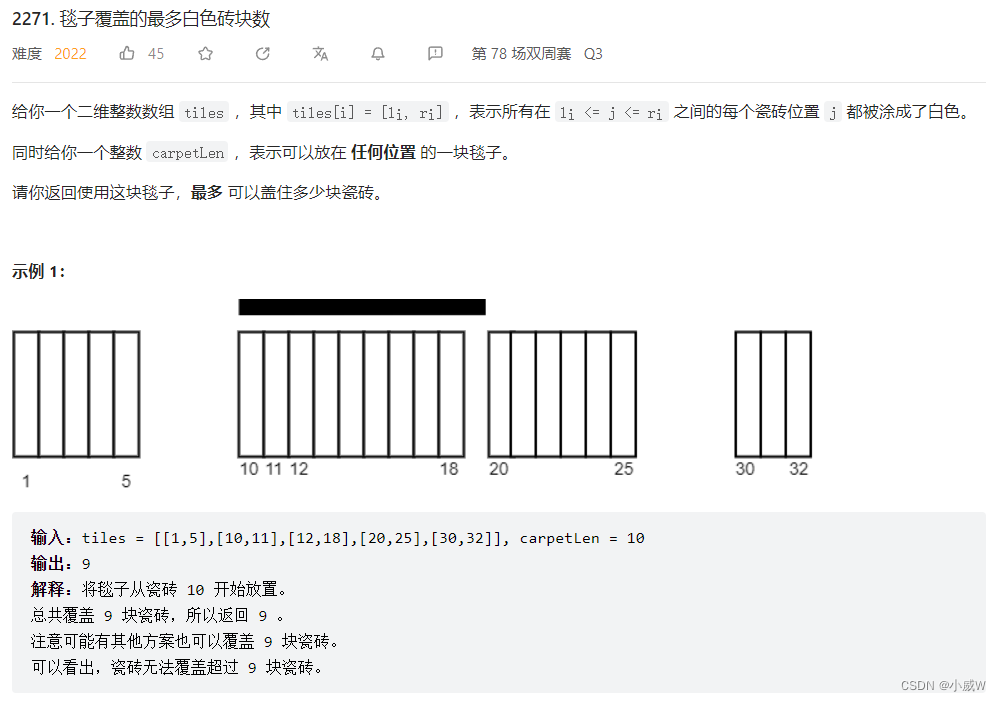
2271. 毯子覆盖的最多白色砖块数
在这里插入图片描述
提示：
1 <= tiles.length <= 5 * 10^4
tiles[i].length == 2
1 <= li <= ri <= 10^9
1 <= carpetLen <= 10^9
tiles 互相不会重叠。

思路

只看题目文本描述比较难以理解，看看图片示例就好了。

朴素的想法就是这块毯子一路滑过去，看看过程中最多会覆盖多少个瓷砖就好了。

但是我们不能枚举位置，而是应该枚举瓷砖大块，也就是枚举 tiles 中的每个元素（看看数据范围就知道为什么了）

在枚举之前，需要先升序排序。

枚举的过程中记录左右端点，计算当前覆盖的瓷砖数（每次计算的瓷砖数是以当前瓷砖块为结尾时，毯子可以覆盖的瓷砖数），更新答案即可。

代码

class Solution {
    public int maximumWhiteTiles(int[][] tiles, int carpetLen) {
        Arrays.sort(tiles, (a, b) -> a[0] - b[0]);
        int ans = 0, sum = 0;
        for (int l = 0, r = 0; r < tiles.length; ++r) {
            sum += tiles[r][1] - tiles[r][0] + 1;   // 记录被覆盖的瓷砖块中一共有几块瓷砖
            while (tiles[l][1] <= tiles[r][1] - carpetLen) {
                sum -= tiles[l][1] - tiles[l][0] + 1;
                ++l;
            }
            // 更新答案时需要减去第一个瓷砖块中未被覆盖的瓷砖
            ans = Math.max(ans, sum - Math.max(0, (tiles[r][1] - carpetLen - tiles[l][0] + 1)));
        }
        return ans;
    }
}

在这里插入图片描述

吐槽：这道题难度居然有 2022，应该是好多人没看懂题。

2302. 统计得分小于 K 的子数组数目

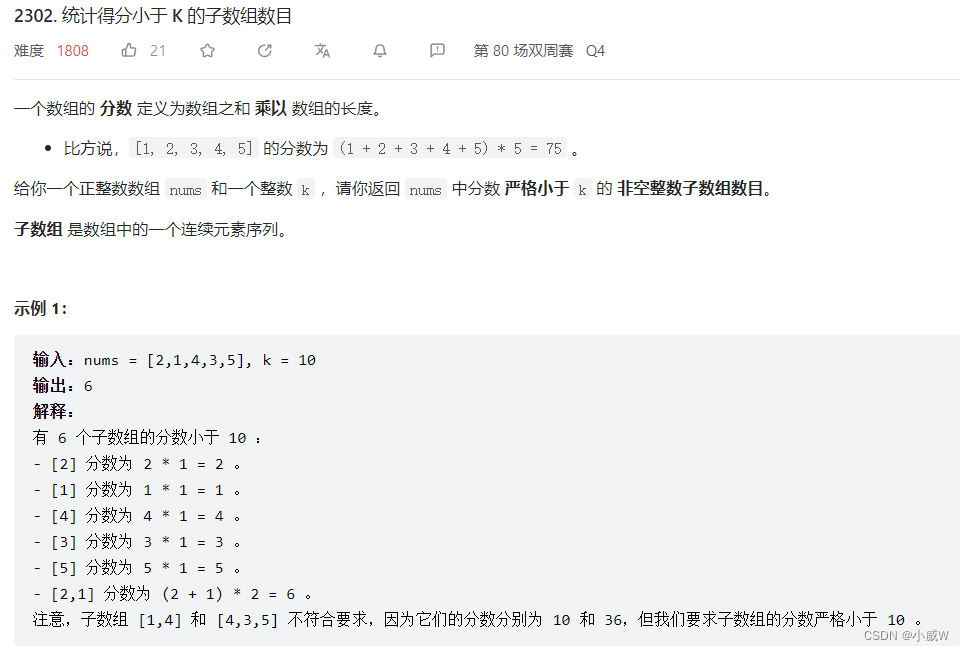
2302. 统计得分小于 K 的子数组数目
在这里插入图片描述

提示：
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^5
1 <= k <= 10^15

代码1——前缀和+滑动窗口

由于需要计算子数组的元素之和，所以可以使用前缀和。

由于元素都是正数，所以显然子数组越长分数越大，因此可以使用双指针滑动窗口，枚举右边界，移动左边界。

class Solution {
    public long countSubarrays(int[] nums, long k) {
        long ans = 0;
        int n = nums.length;
        long[] sum = new long[n + 1];
        for (int i = 1; i <= n; ++i) sum[i] = sum[i - 1] + nums[i - 1];
        for (int l = 0, r = 0; r < n; ++r) {
            long score =  (sum[r + 1] - sum[l]) * (r - l + 1);
            while (score >= k) {
                ++l;
                score =  (sum[r + 1] - sum[l]) * (r - l + 1);
            }
            ans += r - l + 1;
        }
        return ans;
    }
}

代码2——双指针+ $O (1)$ 空间（代码1的优化）

https://leetcode.cn/problems/count-subarrays-with-score-less-than-k/solution/by-endlesscheng-b120/

可以优化一下，将计算前缀和的过程放进双指针过程中，省去前缀和数组。

class Solution {
    public long countSubarrays(int[] nums, long k) {
        long ans = 0, sum = 0;
        for (int l = 0, r = 0; r < nums.length; ++r) {
            sum += nums[r];
            while (sum * (r - l + 1) >= k) {
                sum -= nums[l++];
            }
            ans += r - l + 1;
        }
        return ans;
    }
}