引言
本着“凡我不能创造的,我就不能理解”的思想,本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架,该框架类似PyTorch能实现自动求导。
💡系列文章完整目录: 👉点此👈
要深入理解深度学习,从零开始创建的经验非常重要,从自己可以理解的角度出发,尽量不适用外部框架的前提下,实现我们想要的模型。本系列文章的宗旨就是通过这样的过程,让大家切实掌握深度学习底层实现,而不是仅做一个调包侠。
本文我们来了解注意力机制。在前面几篇文章讨论的seq2seq模型,非常依赖上下文向量。而上下文向量只是最后一个时间步的隐藏状态。它可能会成为一个瓶颈,因为输入序列的长度可能是任意的,我们期望一个固定大小的隐藏向量保存任意长度的信息是不可能的。
注意力机制就为了解决这个瓶颈,它允许解码器可以从编码器所有的隐藏状态中获取信息,而不仅仅是最后一个隐藏状态。
注意力机制
注意力机制是论文NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE提出来的,建议去看原文,也可以看笔者尝试的翻译 :[论文翻译]NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE。

传统的seq2seq模型,编码器读取了整个输入序列后,会为每个时间步都生成一个隐藏状态,但只是取最后一个隐藏状态作为固定大小的上下文向量传递给解码器。
而在注意力机制中,上下文向量通过一个函数生成,该函数读编码器所有时刻的隐藏状态:
c
=
f
(
h
1
e
,
⋯
,
h
n
e
)
(1)
\pmb c= f(\pmb h_1^e,\cdots,\pmb h_n^e) \tag 1
c=f(h1e,⋯,hne)(1)
这里用
c
\pmb c
c表示这个上下文向量。因为输入序列的长度
n
n
n是不固定的,所以我们一般还是只能用一个向量来表示。
那为什么叫注意力呢?因为就像我们人类注意一副图片一样。

比如说上面这幅图片,博主第一眼注意到的是里面的人。随着眼球的移动又看到了电线杆啥的。
对于注意力机制来说,也是类似的,虽然编码器输出了 n n n个隐藏状态,但我们只会注意到少数部分,就像我们每次都看到图片的某个部分一样。怎么强调注意到少数部分呢?实际上通过权重参数来实现的。就是给这几个少数部分增加较大的权重,其他剩下的部分很小的权重。
对于解码器正要生成的token来说,通过为编码器生成的每个隐藏状态赋予不同的权重来仅注意此时感兴趣的相关的(编码器的)输入,然后编码器器的每个隐藏状态都会有一个权重,对它们计算加权和就得到了我们要的上下文向量
c
\pmb c
c:
c
i
=
∑
j
=
1
n
α
i
j
h
j
e
(2)
\pmb c_i = \sum_{j=1}^n \alpha_{ij} \pmb h_j^e \tag 2
ci=j=1∑nαijhje(2)
由于是与解码器的位置相关的,
c
i
\pmb c_i
ci表示在解码步骤
i
i
i重新生成的,从公式可以看出,它考虑了所有编码器的隐藏状态。然后,在解码过程中计算当前时间步解码器隐藏状态时就可以使用此上下文:
h
i
d
=
g
(
y
^
i
−
1
,
h
i
−
1
d
,
c
i
)
(3)
\pmb h_i^d = g(\hat y_{i-1}, \pmb h_{i-1}^d, \pmb c_i) \tag{3}
hid=g(y^i−1,hi−1d,ci)(3)
这个公式和我们上篇文章中看到的公式很像:
h
i
d
=
g
(
y
^
i
−
1
,
h
i
−
1
d
,
c
)
\pmb h_i^d = g(\hat y_{i-1}, \pmb h_{i-1}^d , \pmb c)
hid=g(y^i−1,hi−1d,c)
不过在公式
(
3
)
(3)
(3)中的上下向量
c
i
\pmb c_i
ci不再是静态的。
从公式 ( 3 ) (3) (3)也可以看出重要的一点,即先后问题,先有 c i \pmb c_i ci后才有的 h i d \pmb h_i^d hid,说明无法通过当前位置解码器的隐藏状态来计算 c i \pmb c_i ci,而是通过上一位置的隐藏状态 h i − 1 d \pmb h_{i-1}^d hi−1d计算的!
只要能通过某种机制生成注意力权重,那么在解码器不同的时间步上可以注意到编码器不同的输入,得到的上下文向量也是不同的。相当于此时的上下文向量不再是固定的,而是解码器动态生成的感兴趣的。
现在的问题是,这个注意力权重要如何生成。
注意力权重也可以理解为相关性,说到相关性大家应该能想到余弦相似度,对于两个向量
a
\pmb a
a和
b
\pmb b
b来说,它们的余弦相似度就是:
similarity
=
a
⋅
b
∣
∣
a
∣
∣
∣
∣
b
∣
∣
\text{similarity} = \frac{\pmb a \cdot \pmb b}{||\pmb a|| \,||\pmb b||}
similarity=∣∣a∣∣∣∣b∣∣a⋅b
分母是为了归一化,得到的是一个标量,那么不难想到一种最简单的方法就是计算这两个向量的点乘,这种方法称为点乘注意力(dot-product attention):
score
(
h
i
−
1
d
,
h
j
e
)
=
h
i
−
1
d
⋅
h
j
e
(4)
\text{score}(\pmb h_{i-1}^d,\pmb h^e_j) = \pmb h^d_{i-1}\cdot \pmb h^e_j \tag{4}
score(hi−1d,hje)=hi−1d⋅hje(4)
这里再次强调一下,上标
d
d
d表示Decoder,解码器;上标
e
e
e表示Encoder,编码器。
所以是用解码器第 i − 1 i-1 i−1个位置的隐藏状态与编码器第 j j j个位置的隐藏状态做点积得到的标量(得分)作为注意力得分,这个得分的取值范围应该是实数空间。
编码器共有
n
n
n个输入,我们就可以通过
h
i
−
1
d
\pmb h_{i-1}^d
hi−1d得到
n
n
n个注意力得分,即
n
n
n个标量,这
n
n
n个标量如何变成权重呢?很简单,通过Softmax即可:
α
i
j
=
softmax
(
score
(
h
i
−
1
d
,
h
j
e
)
)
=
exp
(
score
(
h
i
−
1
d
,
h
j
e
)
)
∑
k
=
1
n
exp
(
score
(
h
i
−
1
d
,
h
k
e
)
)
(5)
\begin{aligned} \alpha_{ij} &= \text{softmax}(\text{score}(\pmb h^d_{i-1},\pmb h^e_j)) \\ &= \frac{\exp(\text{score}(\pmb h^d_{i-1},\pmb h^e_j))}{\sum_{k=1}^n \exp(\text{score}(\pmb h^d_{i-1},\pmb h^e_k))} \end{aligned} \tag 5
αij=softmax(score(hi−1d,hje))=∑k=1nexp(score(hi−1d,hke))exp(score(hi−1d,hje))(5)
这样得到的
α
\alpha
α就是0到1之间的一个权重。
再利用公式 ( 2 ) (2) (2)就可以得到当前时间步 i i i需要的上下文向量 c i \pmb c_i ci。
最后用一张图片来总结注意力计算的过程:
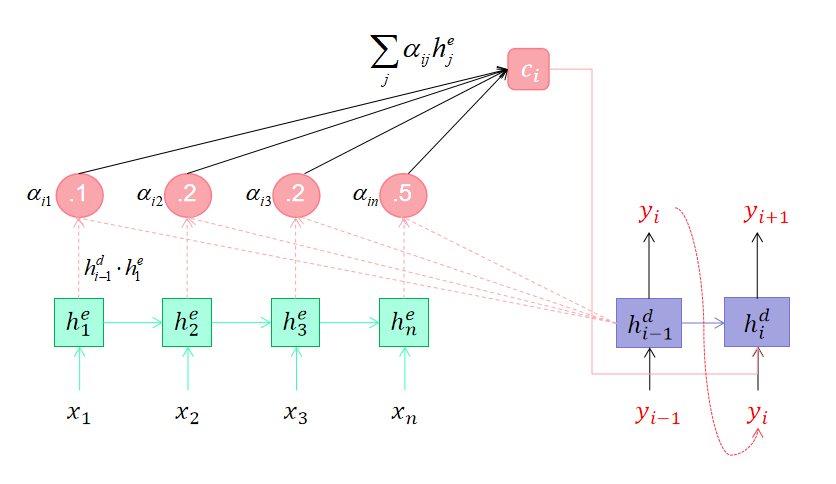
- 在计算 h i d h_i^d hid时先用 h i − 1 d h_{i-1}^d hi−1d与编码器所有的隐状态计算点积,然后计算Softmax得到权重 α \alpha α
- 用权重 α \alpha α和编码器所有的隐状态计算加权和,得到上下文向量 c i c_i ci
- 用 c i , h i − 1 d c_i,h_{i-1}^d ci,hi−1d和上一步的输出 y i y_i yi计算当前时间步的隐状态 h i d h_i^d hid
- 利用 h i d h_i^d hid计算当前时间步的输出 y i + 1 y_{i+1} yi+1
以上就是注意力机制的内容,是不是也挺简单的。
我们上面介绍的是点乘注意力,其实还有很多其他的注意力。
常见注意力方式
为了表示方便,我们用 q \pmb q q和 k \pmb k k分别表示解码器的隐藏状态和编码器的隐藏状态向量。
q
i
\pmb q_i
qi是某个时刻
i
i
i的隐藏状态向量,它的形状是batch_size, decoder_hidden_size;
k
\pmb k
k是编码器最顶层输出的所有隐藏状态向量,它的形状是src_len, batch_size, encoder_hidden_size;
点积注意力
点积注意力,我们上面介绍的。它要求编码器的
score
(
q
i
,
k
)
=
q
i
⋅
k
(6)
\text{score}(\pmb q_i,\pmb k) = \pmb q_i \cdot \pmb k \tag{6}
score(qi,k)=qi⋅k(6)
优点是计算效率高,只需要计算点积。
缩放点积注意力
score ( q i , k ) = q i ⋅ k d k (7) \text{score}(\pmb q_i,\pmb k) = \frac{\pmb q_i\cdot \pmb k}{\sqrt{d_k}} \tag{7} score(qi,k)=dkqi⋅k(7)
但是点积运算有很大的方差,导致Softmax函数的梯度较小。因此缩放点积注意力除以一项来平滑分数的值,来缓解这个问题。
General注意力
score ( q i , k ) = q i T W k (8) \text{score}(\pmb {q_i},\pmb k) = \pmb q_i^T W\pmb k \tag{8} score(qi,k)=qiTWk(8)
和点积注意相比,引入了一个权重 W W W,使得编码器和解码器的大小可以不一致,在计算相似度时引入了非对称性。
上式可以改成为 q i T W k = q i T ( U T V ) k = ( U q i ) T ( V k ) \pmb q_i^T W\pmb k = \pmb q_i^T (U^TV)\pmb k = (U \pmb q_i )^T (V\pmb k) qiTWk=qiT(UTV)k=(Uqi)T(Vk),即分别对 q \pmb q q和 k \pmb k k进行线性变换之后再计算点积。
加性注意力
score ( q i , k ) = v T tanh ( W q i + U k ) (9) \text{score}(\pmb {q_i},\pmb k) = \pmb v^T \tanh(W\pmb q_i + U\pmb k) \tag{9} score(qi,k)=vTtanh(Wqi+Uk)(9)
加性注意力引入了可学习的参数,将 q \pmb q q和 k \pmb k k映射到不同的空间后进行打分。
各种注意力做的事情其实都是为了在生成输出词时,考虑每个输入词和当前输出词的对齐关系,对齐越好的词,会有越大的权重,对生成当前输出词的影响也越大。
代码实现
class Attention(nn.Module):
def __init__(self, enc_hid_dim=None, dec_hid_dim=None, method: str = "dot") -> None:
"""
Args:
enc_hid_dim: 编码器的隐藏层大小
dec_hid_dim: 解码器的隐藏层大小
method: dot | scaled_dot | general | bahdanau | concat
Returns:
"""
super().__init__()
self.method = method
self.encoder_hidden_size = enc_hid_dim
self.decoder_hidden_size = dec_hid_dim
if self.method not in ["dot", "scaled_dot", "general", "bahdanau", "concat"]:
raise ValueError(self.method, "is not an appropriate attention method.")
if self.method == "general":
self.linear = nn.Linear(self.encoder_hidden_size, self.decoder_hidden_size, bias=False)
elif self.method == "bahdanau":
self.W = nn.Linear(self.decoder_hidden_size, self.decoder_hidden_size, bias=False)
self.U = nn.Linear(self.encoder_hidden_size, self.decoder_hidden_size, bias=False)
self.v = nn.Linear(self.decoder_hidden_size, 1, bias=False)
elif self.method == "concat":
# concat
self.linear = nn.Linear((self.encoder_hidden_size + self.decoder_hidden_size), self.decoder_hidden_size,
bias=False)
self.v = nn.Linear(self.decoder_hidden_size, 1, bias=False)
def _score(self, hidden: Tensor, encoder_outputs: Tensor) -> Tensor:
"""
Args:
hidden: (batch_size, decoder_hidden_size) 解码器前一时刻的隐藏状态
encoder_outputs: (src_len, batch_size, encoder_hidden_size) 编码器的输出(隐藏状态)序列
Returns:
"""
src_len, batch_size, encoder_hidden_size = encoder_outputs.shape
if self.method == "dot":
# 这里假设编码器和解码器的隐藏层大小一致,如果不一致,不能直接使用点积注意力
# (batch_size, hidden_size) * (src_len, batch_size, hidden_size) -> (src_len, batch_size, hidden_size)
# (src_len, batch_size, hidden_size).sum(axis=2) -> (src_len, batch_size)
return (hidden * encoder_outputs).sum(axis=2)
elif self.method == "scaled_dot":
# 和点积注意力类似,不过除以sqrt(batch_size),也可以指定一个自定义的值
return (hidden * encoder_outputs / math.sqrt(encoder_hidden_size)).sum(axis=2)
elif self.method == "general":
# energy = (src_len, batch_size, decoder_hidden_size)
energy = self.linear(encoder_outputs)
# (batch_size, decoder_hidden_size) * (src_len, batch_size, decoder_hidden_size)
# -> (src_len, batch_size, decoder_hidden_size)
# .sum(axis=2) -> (src_len, batch_size)
return (hidden * energy).sum(axis=2)
elif self.method == "bahdanau":
# hidden = (batch_size, decoder_hidden_size)
# encoder_outputs = (src_len, batch_size, encoder_hidden_size)
# W(hidden) -> (batch_size, decoder_hidden_size)
# U(encoder_outputs) -> (src_len, batch_size, decoder_hidden_size)
# energy = (src_len, batch_size, decoder_hidden_size)
energy = F.tanh(self.W(hidden) + self.U(encoder_outputs))
# v(energy) -> (src_len, batch_size, 1)
# squeeze -> (src_len, batch_size)
return self.v(energy).squeeze(2)
else:
# concat
# unsqueeze -> (1, batch_size, decoder_hidden_size)
# hidden = (src_len, batch_size, decoder_hidden_size)
hidden = hidden.unsqueeze(0).repeat(src_len, 1, 1)
# encoder_outputs = (src_len, batch_size, encoder_hidden_size)
# cat -> (src_len, batch_size, encoder_hidden_size +decoder_hidden_size)
# linear -> (src_len, batch_size, decoder_hidden_size)
energy = F.tanh(self.linear(F.cat((hidden, encoder_outputs), axis=2)))
# v -> (src_len, batch_size , 1)
# squeeze -> (src_len, batch_size)
return self.v(energy).squeeze(2)
def forward(self, hidden: Tensor, encoder_outputs: Tensor) -> Tuple[Tensor, Tensor]:
"""
Args:
hidden: (batch_size, decoder_hidden_size) 解码器前一时刻的隐藏状态
encoder_outputs: (src_len, batch_size, encoder_hidden_size) 编码器的输出(隐藏状态)序列
Returns: 注意力权重, 上下文向量
"""
# (src_len, batch_size)
attn_scores = self._score(hidden, encoder_outputs)
# (batch_size, src_len)
attn_scores = attn_scores.T
# (batch_size, 1, src_len)
attention_weight = F.softmax(attn_scores, axis=1).unsqueeze(1)
# encoder_outputs = (batch_size, src_len, num_hiddens)
encoder_outputs = encoder_outputs.transpose((1, 0, 2))
# context = (batch_size, 1, num_hiddens)
context = F.bmm(attention_weight, encoder_outputs)
# context = (1, batch_size, num_hiddens)
context = context.transpose((1, 0, 2))
return attention_weight, context
上面是各种注意力机制的代码实现,其中点积注意力要求编码器和解码器隐藏层大小一致。
参考
- Seq2Seq中常见注意力机制的实现