浅谈线段树

1.前言

Oi-Wiki上的线段树

同步于 $c nb l o g s$ 发布。

如有错误，欢迎各位 dalao 们指出。

注：本篇文章个人见解较多，如有不适，请谅解。

前置芝士

1.二叉树的顺序储存

2.线段树是什么？

线段树，英文为 $S e g m e n t$ $t ree$ 。它是一种数据结构，主要解决区间修改和区间查询的问题。

我们用一个例题来引入线段树。

引例:

现在给定一个长度为 $n$ （ $n\le 10^6$ ）的序列 $a$ 。然后现在有 $m$ （ $m\le 10^6$ ）个询问操作，对于每一个操作，都有两种情况：

1 x y，这一种操作表示将 $a_x$ 加上 $y$ 。
2 l r，这一种操作表示查询 $l - r$ 这个区间的区间和，并输出。

对于这样的一个问题，不难发现，这是一个单点修改，区间查询的题目。

3.单点修改线段树

显然，对于刚才那道例题，我们运用暴力或者前缀和的思想在最坏情况下都会被卡到 $O (nm)$ ，肯定是过不了这个题目的，如果要过这个题目，差不多也必须是在 $O (n l o g m)$ 或者 $O (m l o g n)$ 时间复杂度以内的算法才能够承受。因此，我们的线段树算法就此横空出世！

其实我们在学树状数组的时候，我们有一种思想就是我们通过二进制分解将一个区间化为 $l o g n$ 个子区间。那

我们可以将 $a$ 序列的 $1$ 到 $n$ 这个区间化成左右两个区间。为了方便举例，我们假定现在 $n = 5$ 。显然，我们可以把 $[1, n]$ 化为区间 $[1, 2]$ 和区间 $[3, 5]$ 。现在定义一个区间的左右两个区间分别为这个区间的左孩子和右孩子。例如现在的区间为 $[x, y]$ ，则他的左孩子就是 $[x, (x + y) /2]$ ，右孩子就是 $[(x + y) /2 + 1, y]$ 。特别要注意的是如果 $x = y$ ，则他就是叶子节点，因为这个区间已经不能再分了。

则我们现在就可以把一个 $n = 5$ 的序列化为一棵树。

qwq

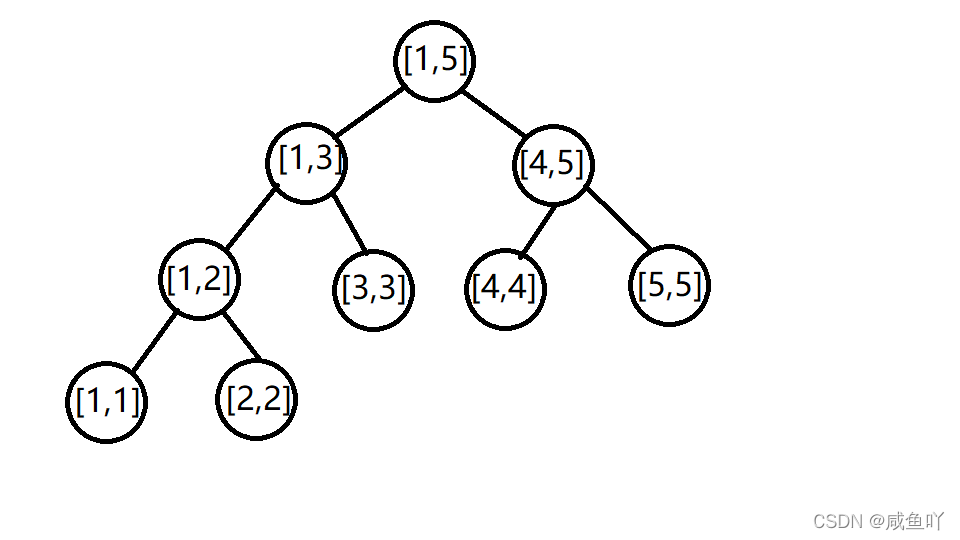
如图，我们可以发现，所有叶子节点的区间左端点和右端点都是相等的。并且由于我们需要的是区间和，所以我们需要把书上每个区间的和的统计出来。我们可以根节点 $[1, 5]$ 这个区间编号为 $1$ ，则通过二叉树的顺序储存原理，编号为 $x$ 的节点，他的左儿子为 $2 x$ ，右儿子为 $2 x + 1$ 。为了方便查询一个区间的左儿子和右儿子，我们就运用这种顺序储存原理来储存这课树。

我们可以运用递归来进行建树。

建树参考代码如下:

struct segmentree
{
	int l,r;//当前节点的左端点和右端点
	long long data;//当前这个区间的区间和
}tree[maxe];//顺序储存，maxe 表示 4*n。（仔细想一想为什么要开4倍）
void build(int p,int l,int r)//p表示节点，l,r表示当前节点的做右端点
{
	if(l==r)//如果左右端点相等，就表明这个节点是叶子节点，并用继续递归下去了。
	{
   	  //将当前节点的三个信息储存下来。
		tree[p].l=l;
		tree[p].r=r;
		tree[p].data=a[l];
		return;
	}
	int mid=(l+r)>>1;
    //对他的左右儿子进行建树
	build(p*2,l,mid);
	build(p*2+1,mid+1,r);
	tree[p].l=l,tree[p].r=r;
	tree[p].data=tree[p*2].data+tree[p*2+1].data;//由于当前区间有左右孩子，所以当前区间的区间和就等于他的左右孩子的区间和之和。
}

建完树之后，接下来的问题就是修改操作。

我们可以发现，如果修改了第 $x$ 位上的值，则所有包含了 $x$ 的区间的区间和都要改变，也就是对一个 $n = 5, x = 3$ 的树， $a_x$ 被修改了之后，我们需要将途中所有标橙了的区间的区间和修改掉。

qwq

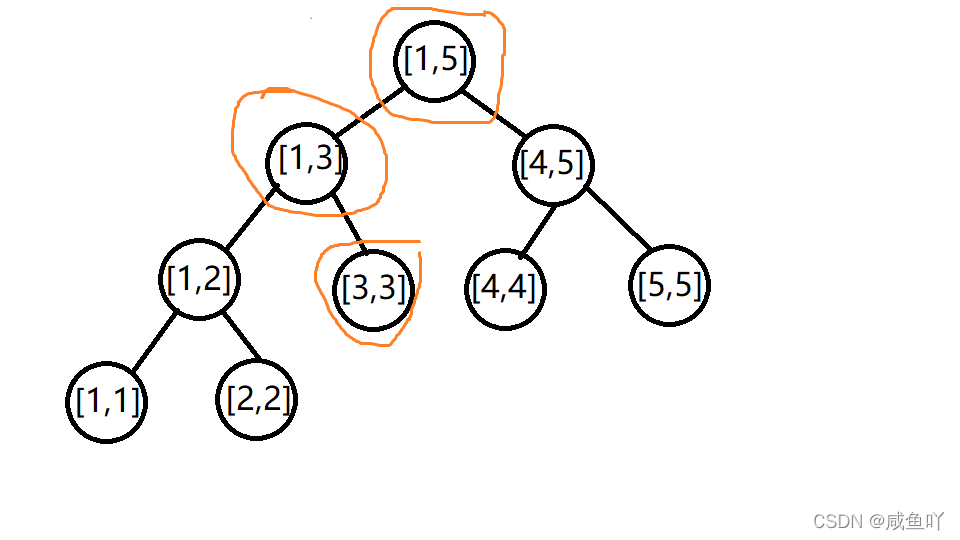
可以发现，你无论修改的是哪一位上的数值，要被改动的区间和最坏是 $(l o g n + 1)$ （向上取整）次，所以时间复杂度为 $m l o g n$ 。

对于修改操作的代码实现，仍然使用递归。

修改操作参考代码:

void change(int p,int x,int y)//p表示当前递归到的节点编号，x,y表示将a[x]改为y
{
	if(tree[p].l>x||tree[p].r<x)//如果当前这个节点的区间不包含x,则不需要在递归下去。
	return;
   	if(tree[p].l==x&&tree[p].r==x)
   	{
   		tree[p].data+=y;
   		return;
	}
  	//对他的孩子进行递归。
	change(p*2,x,y);
	change(p*2+1,x,y);
	tree[p].data=tree[p*2].data+tree[p*2+1].data;//当前区间的区间和就是他的左右儿子之和 
}

最后就是查询区间和操作。

比较容易发现，我们如果要查询 $[l, r]$ 区间的区间和，这个区间可以在我们拆出来的二叉树中找到 $l o g n$ 个极大区间，而我们只需要把所有拆分出来的这些区间的和给统计起来即可。时间复杂度仍然为 $O (m l o g n)$ 。

区间查询参考代码:

long long ask(int p,int l,int r)//p表示当前节点编号，l,r表示要查询的[l,r]区间
{
	if(tree[p].r<l||tree[p].l>r)//如果当前枚举到的区间与查询的区间没有交集，则就没有必要在查询下去了
	return 0;
	if(tree[p].r<=r&&tree[p].l>=l)//如果要查询的区间包含现在美剧道德区间，则我们就直接返回这个区间的区间和
	{
		return tree[p].data;
	}
	long long res=0;
	res+=ask(p*2,l,r)+ask(p*2+1,l,r);//继续递归下去的时候，要把它的左右孩子递归得到的值给储存下来。
	return res;
}

4.线段树求区间最大最小值

上面我们讲的是线段树快速求出一个区间 $[l, r]$ 的区间和，现在我们要讨论的就是如何运用线段树求出 $[l, r]$ 求出一个区间的最大最小值。

我们现在直接以求最大值进行举例。

对于建树，由于是求最大值，所以我们应该将建树的倒数第二行改成求两个左右儿子节点的最大值。

建树参考代码如下:

void build(int p,int l,int r)
{
	if(l==r)
	{
		tree[p].l=l;
		tree[p].r=r;
		tree[p].data=a[l];
		return;
	}
	int mid=(l+r)>>1;
	build(p*2,l,mid);
	build(p*2+1,mid+1,r);
	tree[p].l=l,tree[p].r=r;
	tree[p].data=max(tree[p*2].data,tree[p*2+1].data);//与区间和的唯一区别就在这里，是求最大值而不是求和
}

对于单点修改，我们同样需要修改倒数第二行，因为它是取最大值。特别要注意的是，如果当前递归道的区间就是 $[x, x]$ ，则我们需要直接将这个区间的最大值设为 $y$ ，因为他的修改操作是 $a_x=y$ 。

修改操作参考代码如下:

void change(int p,int x,int y)
{
	if(tree[p].l>x||tree[p].r<x)
	return;
	if(tree[p].l==x&&tree[p].r==x)
	{
		tree[p].data=y;//直接设为y
		return;
	}
	change(p*2,x,y);
	change(p*2+1,x,y);
	tree[p].data=max(tree[p*2].data,tree[p*2+1].data);//这里是区最大值
}

最后是查询操作，这个也一样，因为是求最大值，所以我们仍然只需要改成 $ma x$ 即可。

查询操作参考代码如下:

int ask(int p,int l,int r)
{
	if(tree[p].r<l||tree[p].l>r)
	return INT_MIN;
	if(tree[p].r<=r&&tree[p].l>=l)
	{
		return tree[p].data;
	}
	int res=0;
	res=max(ask(p*2,l,r),ask(p*2+1,l,r));//注意是最大值
	return res;
}

5.线段树的区间修改以及懒惰标记

上文中，我们讲到了线段树可以维护单点修改，区间查询最大值和区间和。这时，你可能会问，那是不是线段树就不支持区间修改了呢？

Too young to simple! 线段树这么有用的数据结构怎么可能维护不了区间修改这种东西。那么接下来，就给大家介绍如何运用线段树解决区间修改的问题，

先抛出一个例题，洛谷 P3372 【模板】线段树 1。

读完题目后，你发现，这不就是线段树区间修改和区间查询的模板题吗？

对于这个题目，要用线段树做的话我们首先是建树。对于这一个建树的话没有什么可以说的，跟线段树的普通建树一样，这里不做过多阐述。

现在最头疼的就是这个区间修改操作，我们知道，如果要修改整个区间且运用普通线段树，则我们需要将所有与这个区间有交集的区间的区间和都要修改，速度最慢可以卡到 $O (n)$ ，还没有普通的暴力快，那我们该怎么办呢？

这个时候，我们要引入一个叫做懒惰标记的东西。

我们可以对于树上的每一个节点再定义一个东西，叫做 $l a zy t a g$ 。我们运用它来储存这整个区间整体每个数被加了多少。例如我们现在将 $[1, 5]$ 这个区间全部加上 $3$ 。则对于区间 $[2, 4]$ 来说，它的 $l a zy t a g$ 就等于 $3$ 。

当我们在递归修改时，如果当前要修改的这个区间包含了现在遍历到的节点的区间，则我们就将它的 $l a zy t a g +$ 要区间加的值，并将整个区间的区间和修改。如果当前遍历到的区间只与要修改的区间存在交集，那对于普通的线段树，我们就要对他的左右儿子进行遍历。但是由于当前枚举到的这个区间的懒惰标记只记录了这个区间的，而我们还没有对它进行下传，且马上又要遍历他的子节点。所以这个时候我们就需要将这个懒惰标记下传到它的子节点身上，并修改相应的值，再进行对它儿子的递归。

修改操作参考代码如下:

void pushdown(int p)//这是懒惰标记下传操作
{
	if(tree[p].lazytag)//如果当前节点有懒惰标记需要下传
	{
		int l=p*2,r=p*2+1;//l,r分别表示当前节点的左右儿子
		long long tag=tree[p].lazytag;//tag来记录当前节点的懒惰标记
		tree[l].data+=(long long)(tree[l].r-tree[l].l+1)*tag;//下传的途中，我们需要将两个区间的和都进行修改，也就是加上区间长度*懒惰标记。
		tree[r].data+=(long long)(tree[r].r-tree[r].l+1)*tag;//同上
		tree[l].lazytag+=tag;//对懒惰标记进行下传
		tree[r].lazytag+=tag;//同上
		tree[p].lazytag=0;//下传完之后要将当前节点的懒惰标记清零，因为已经下传
	}
}
void change(int p,int l,int r,long long x)
{
	if(tree[p].l>r||tree[p].r<l)//如果不存在交集，就不需要再进行递归了
	return;
	if(tree[p].l>=l&&tree[p].r<=r)
	{
		tree[p].data+=(long long)(tree[p].r-tree[p].l+1)*x;//区间长度呈上要修改的值
		tree[p].lazytag+=x;//修改懒惰标记
		return;
	}
	pushdown(p);//标记下传
   	//普通线段树的递归操作
	change(p*2,l,r,x);
	change(p*2+1,l,r,x);
	tree[p].data=tree[p*2].data+tree[p*2+1].data; 
}

最后就是区间查询，在区间查询的时候，我们如果当前要查询的区间和枚举到的节点的区间存在交集，则我们同样需要更新他左右儿子的值并下传懒惰标记，其余的都不需要改变。

区间查询参考代码:

long long ask(int p,int l,int r)
{
	if(tree[p].r<l||tree[p].l>r)
	return 0;
	if(tree[p].r<=r&&tree[p].l>=l)
	{
		return tree[p].data;
	}
	pushdown(p);//与普通线段树的唯一区别就是这里要下传懒惰标记和修改左右子节点的区间和，因为后面需要查询左右儿子的信息。
	long long res=0;
	res=ask(p*2,l,r)+ask(p*2+1,l,r);
	return res;
}