---

本篇文章涉及题目均来自 leetCode：

• 121.买卖股票的最佳时机（简单）: 限定交易次数 k=1
• 122. 买卖股票的最佳时机 II（中等） : 交易次数无限制 k = +infinity
• 123.买卖股票的最佳时机 III (困难) : 限定交易次数 k=2
• 188.买卖股票的最佳时机 IV (困难) : 限定交易次数 最多次数为 k
• 309.最佳买卖股票时机含冷冻期(中等) : 含有交易冷冻期
• 714.买卖股票的最佳时机含手续费 (中等) : 每次交易含手续费

小温建议各位小伙伴看完，立马去leetCode上手写写，毕竟俗话说的好： 好记性不如烂笔头 ！

一、基础题目

接下来，就由小温带大家解决 “买卖股票”系列算法题， 以最基础的 121 题：买卖股票的最佳时机（简单） 为例，讲解解决思路：

> 题目

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票（ 此段话表示，只允许交易一次，也就是买和卖各一次。k = 1 ）。

设计一个算法来计算你所能获取的最大利润，返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

> 解题思路

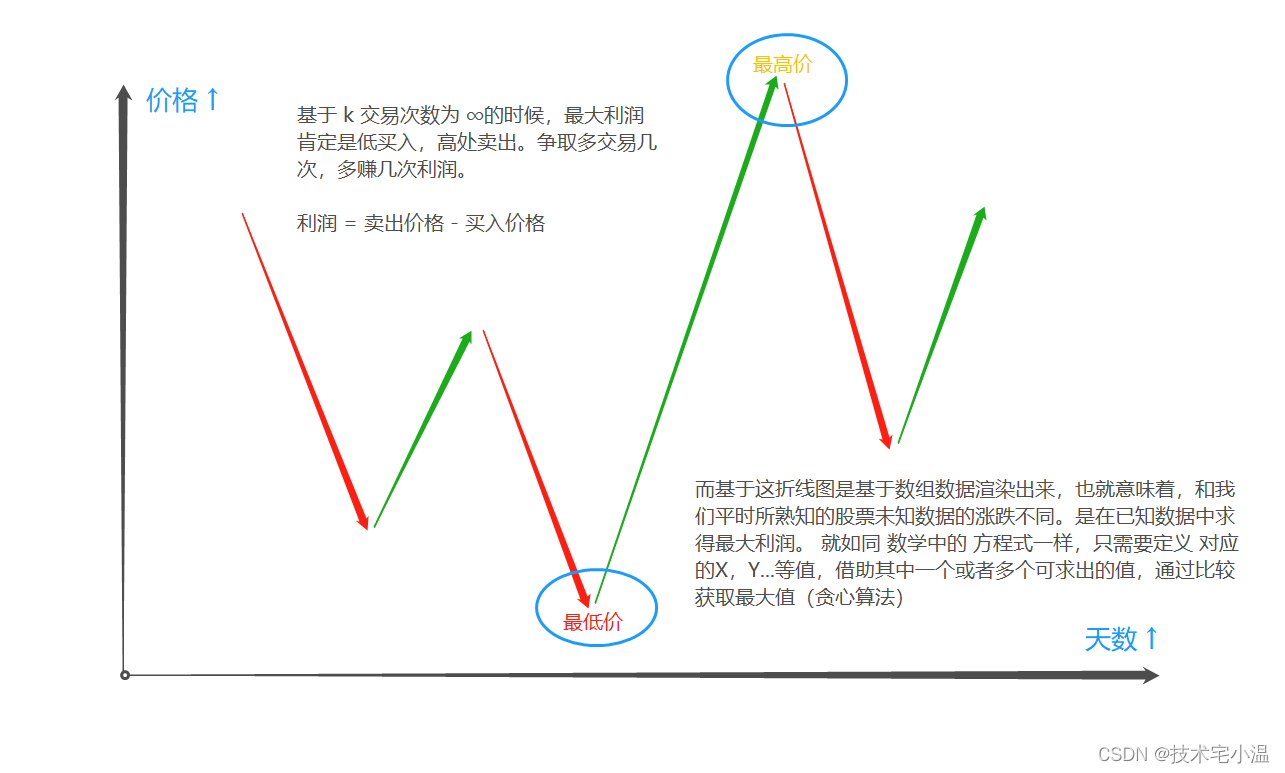
通过上图可以知道，我们需要借助已知的数据，配合定义未知的变量去推出最大利润！ 而定义这个推理公式的方法，叫做 “ 动态规划 ”。需要清楚各个数据之间的练习，接下来分析一下需要定义那些已知常量 和 未知的变量。

根据题目可以知道每天的股票的波动数据，结合常识，需要定义以下内容：

定义操作

• 买入
• 卖出
• 不操作

定义状态

• i: 天数
• k: 交易次数，每次交易包含买入和卖出，这里我们只在买入的时候需要将 k - 1
• 0: 不持有股票时，买入费用
• 1: 持有股票时开销，包含购入的价格，所以计算利润时，需要减去购入价格

动态规划值所需变量

• dp[i][k][0] : 第 i 天 第 k 次交易中，手中无股票， 计算公式为：当天股票价格 - 购入股票的费用。
• dp[i][k][1] : 第 i 天 第 k 次交易中，手中有股票，买入股票的费用。

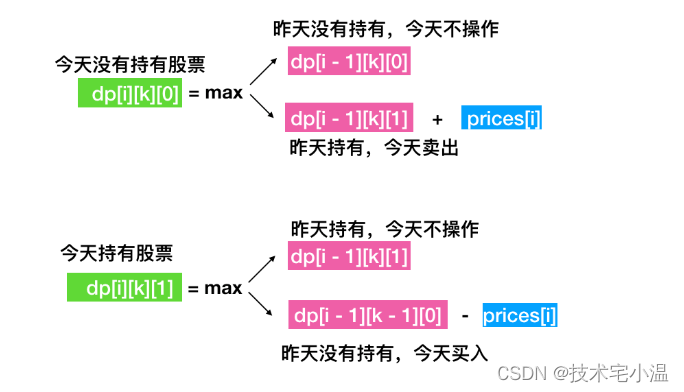
// 今天没有持有股票，分为两种情况
// 1. dp[i - 1][k][0]，昨天没有持有，今天不操作。 
// 2. dp[i - 1][k][1] + prices[i] 昨天持有，今天卖出，今天手中就没有股票了。
dp[i][k][0] = Math.max(dp[i - 1][k][0], dp[i - 1][k][1] + prices[i])


// 今天持有股票，分为两种情况：
// 1.dp[i - 1][k][1] 昨天持有，今天不操作
// 2.dp[i - 1][k - 1][0] - prices[i] 昨天没有持有，今天买入。
dp[i][k][1] = Math.max(dp[i - 1][k][1], dp[i - 1][k - 1][0] - prices[i])

//最大利润就是这俩种情况的最大值

====> 由于 此题k为1，所以转化为以下情况 <====

//第i天不持有 由 第i-1天不持有然后不操作 和 第i-1天持有然后卖出 两种情况的最大值转移过来
dp[i][1][0] = Math.max(dp[i - 1][1][0], dp[i - 1][1][1] + prices[i])

//第i天持有 由 第i-1天持有然后不操作 和 第i-1天不持有然后买入 两种情况的最大值转移过来
dp[i][1][1] = Math.max(dp[i - 1][1][1], dp[i - 1][0][0] - prices[i])
            = Math.max(dp[i - 1][1][1], -prices[i])
            // k=0时 没有交易次数，dp[i - 1][0][0] = 0

k是固定值1，不影响结果，所以可以不用管，简化之后如下：

dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i])
dp[i][1] = Math.max(dp[i - 1][1], -prices[i])

完整代码

//时间复杂度O(n) 空间复杂度O(n)，dp数组第二维是常数
const maxProfit = function (prices) {
    let n = prices.length;
    let dp = Array.from(new Array(n), () => new Array(2));
    dp[0][0] = 0; //第0天不持有
    dp[0][1] = -prices[0]; //第0天持有
    for (let i = 1; i < n; i++) {
        dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
        dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
    }
    return dp[n - 1][0];
};

状态压缩，dp[i] 只和 dp[i - 1] 有关，去掉一维

//时间复杂度O(n) 空间复杂度O(1)
const maxProfit = function (prices) {
	let n = prices.length;
	let dp = Array.from(new Array(n), () => new Array(2));
	dp[0] = 0;
	dp[1] = -prices[0];
	for (let i = 1; i < n; i++) {
	    dp[0] = Math.max(dp[0], dp[1] + prices[i]);
	    dp[1] = Math.max(dp[1], -prices[i]);
	}
	return dp[0];
};

//语意化
const maxProfit = function (prices) {
    let n = prices.length;
    let sell = 0;
    let buy = -prices[0];
    for (let i = 1; i < n; i++) {
        sell = Math.max(sell, buy + prices[i]);
        buy = Math.max(buy, -prices[i]);
    }
    return sell;
};

二、添加条件：当交易次数为 ∞ 时

• 122. 买卖股票的最佳时机 II（中等） : 交易次数无限制 k = +infinity

> 题目

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

示例 1：

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
     总利润为 4 + 3 = 7 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
     总利润为 4 。

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0 。

> 解决思路

股票对应的题目，只要能理解第一题的动态规划公式，能理解推论，基本上大致都相同。在添加交易次数为无穷的时候，只需要在下一次买入时，加上上次交易剩余的利润即可，在 k 同样不影响结果，简化之后如下：

dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i])
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i])

语意化之后的核心代码如下：

sell = Math.max(sell, buy + prices[i])
buy = Math.max(buy, sell - prices[i])

三、添加条件：当交易次数为 K = number 时

• 123.买卖股票的最佳时机 III (困难) : 限定交易次数 k=2

> 题目

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格，和一个整型 k 。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说，你最多可以买 k 次，卖 k 次。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1：

输入：k = 2, prices = [2,4,1]
输出：2
解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例 2：

输入：k = 2, prices = [3,2,6,5,0,3]
输出：7
解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
     随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

> 解决思路

根据题目可以得出，我们不能只基于股票数据数组来循环，需要将每个数据假设它交易 K 次，取所有可能的最大利润值！

所以在我们运算时，需要借助 二维数组 或者是 对象数组 来进行缓存，缓存上次最优解的购入和售出的利润！ 在当次计算时，加上上次交易带来的利润进行运算。

具体逻辑如下：

/**
 * @param {number} k
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function(k, prices) {
    let len = prices.length
	// 定义缓存变量，缓存每次交易的购入和售出费用
    let pricesList = new Array(k)
    for(let j = 0; j <= k; j++) {
        pricesList[j] = {
            buy: -prices[0],
            sell: 0
        }
    }



    for(let i = 0; i < len; i++) {
        for(let j = 1; j <= k; j++) {
            pricesList[j].buy = Math.max(pricesList[j].buy, pricesList[j - 1].sell - prices[i])
            pricesList[j].sell = Math.max(pricesList[j].sell, pricesList[j].buy + prices[i])
        }
    }
    return pricesList[k].sell
};

本质还是和上一题，交易次数为无穷的时差不多的核心代码，属于是换汤不换药了！ 只需要在本次计算时，加上上次剩余的利润即可！

四、添加条件： 每次交易时，扣除 fee 数额的手续费

• 714.买卖股票的最佳时机含手续费 (中等) : 每次交易含手续费

这题是122题的变种，我们需要知道，当每次交易卖出时，为该次交易结束。在交易结束时，对总利润减去本次交易的手续费即可！

核心代码如下：

buy = Math.max(buy, sell - prices[i])
sell = Math.max(sell, buy + prices[i] - fee)

👉 结论

通过本篇文章的讲述，相信大家基本上能搞懂 “ 买卖股票 ” 系列的动态规划公式了，万变不离其宗！ 只要能理解：买入和卖出 及 当天股票价格之间的关系，基本上都能推出了！好了，感谢各位小伙伴读到这里，如果感觉对你有所帮助，请勿吝惜你的小手指呀！给小温一个三连吧！

往期内容 💨

🔥 ＜ 每日算法：一文带你认识 “ 双指针算法 ” ＞

🔥 ＜ 每日小技巧： 基于Vue状态的过渡动画 - Transition 和 TransitionGroup＞

🔥 ＜ JavaScript技术分享： 大文件切片上传 及 断点续传思路 ＞

🔥 ＜ 每日份知识快餐：axios是什么？如何在Vue中 封装 axios ？ ＞

🔥 ＜ 面试知识点：什么是 Node.js ？有哪些优缺点？应用场景？ ＞